Оптимизация магнитного сепаратора

B = B _r + HB _r /Н _СВ,             (1)

где B_r – остаточная индукция. Если же магнит из этого материала снова соединить с арматурой (т.е. закоротить магнитную цепь), то магнитный поток будет восстанавливаться в нем по этой характеристике, так как у магнитов из закрити-ческих материалов прямая магнитного возврата совпадает с характеристикой размагничивания.

Магнитные свойства тела (образца постоянного магнита) отличаются от магнитных свойств веществ. Причиной этого является размагничивающее действие полюсов. Под магнитным полюсом понимается участок поверхности образца, на котором нормальная составляющая намагниченности М отлична от нуля и которая возникает на границах раздела двух магнитных сред. Полюса создают внутри тела поле, которое является размагничивающим полем. Напряженность Н_Р размагничивающего поля пропорциональна намагниченности: Н_Р = NМ , где N – коэффициент размагничивания, зависящий от формы тела [2]-[4]. Подставляя значение размагничивающего поля Н = – Н_Р в классическое соотношение

В = µ ₀ (М+Н) ,           (2)

получают известное выражение, называемое характеристикой формы

В = Н_Р µ ₀ (1–N)/N = – µ ₀ (m–1) Н , где ( m–1 ) = ( N^–1 – 1 )– называется проницаемостью формы.

Характеристика формы представляет собой прямую линию, проведенную из начала координат (рис. 1, линия 2), её наклон определяется значением проницаемости формы. Точка пересечения характеристики размагничивания с характеристикой формы и определяет интенсивность магнитной индукции B_р образца магнита (его рабочую точку).

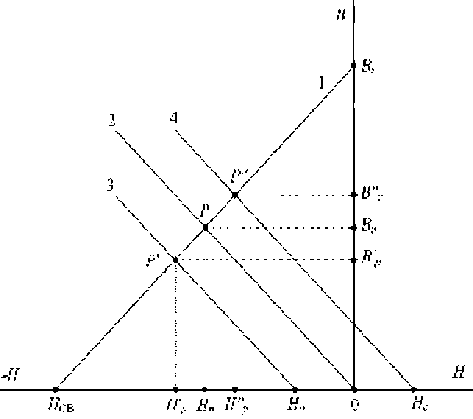
Рис. 1. Типовые характеристики, определяющие магнитное состояние постоянных магнитов из магнитотвердых закритических материалов: 1– характеристика размагничивания материала; 2 – характеристика формы тела магнита при нулевом внешнем поле; 3 – тоже при размагничивающем внешнем поле; 4 – тоже при намагничивающем внешнем поле

При воздействии внешнего поля с напряженностью H₀ магнитная характеристика размагничивания материала в соответствии с [4] принимает вид

B = B_r + ( H ±± H₀ ) B_r/Н_СВ , (3) где знак “–”, если H₀ размагничивающее поле (рис. 1, линия 3) или знак “+”, если H₀ намагничивающее поле (рис. 1, линия 4).

Основные проблемы.

• 1.    При помещении тела магнита в магнитную среду или при изменении его формы при навешивании элементов арматуры меняется наклон характеристики формы и, соответственно, положение рабочей точки постоянного магнита. Вследствие налипания ферромагнитного шлама на магниты сепаратора магнитное состояние постоянных магнитов изменяется. Это обстоятельство необходимо учитывать при анализе поля в сепараторе.

• 2.    Из-за наличия потока рассеяния характеристики магнитов отличается от магнитных характеристик материалов. В работе [5] предложен способ установления связей между характеристиками магнитов с характеристиками материалов на основе представления магнита короткозамкнутой распределенной магнитной цепью.

В задаче оптимизации магнитного сепаратора особое внимание уделяется соотношениям между геометрическими размерами магнитной системы, представляющей собой объемную решетку постоянных магнитов. Поэтому расчетная модель источника поля должна отражать харак- теристики материалов постоянных магнитов и характеристики образцов магнитов. Модель также должна удовлетворять требованию универсальности, должна перестраиваться автоматически при изменении характеристик магнитной среды. Таким требованиям отвечают магнитные цепи. При этом текущей задачей становится объединение решения проблемы 1 и 2 в рамках схем замещений магнитной цепи сепаратора.

СХЕМА ЗАМЕЩЕНИЯ МАГНИТА ДЛЯ МОДЕЛИРОВАНИЯ ПОЛЯ В НЕОДНОРОДНОЙ СРЕДЕ

Магнитный сепаратор – сложный и неоднородный по объему источник магнитного поля. Неоднородность поля обусловлена тремя причинами: 1 – каждым элементом поля (постоянным магнитом); 2 – объемной решеткой этих элементов; 3 – неоднородностью среды, состоящей из арматуры конструкции сепаратора (полюсные наконечники, ферромагнитные опоры и стенки), слоев шлама, налипших на магниты, и намагниченной суспензии.

Таким образом, распределение магнитного поля сепаратора определяется совокупным влиянием системы многих и неоднородных магнитных элементов.

Для анализа поля в системе неоднородных элементов наиболее подходит метод магнитных цепей. Он подразумевает эквивалентную замену физического пространства сепаратора совокупностью магнитных источников и магнитных проводимостей.

Метод магнитных цепей широко применялся в расчетах магнитных систем до 70-х годов двадцатого века [4, 6, 7]. При этом схемы замещения постоянных магнитов преподносились умозрительно [4, 7].

Ниже приводим строгое обоснование схемы замещения постоянного магнита на основе использования идеи распределенной магнитной цепи, предложенной в работе [5]. Недостатком методики, изложенной в работе [5], в том, что формулы связи параметров магнита с параметрами образца получаются в форме нестрогих допущений и итерационных приближений.

В отличие от [5], где применялась распределенная пассивная магнитная цепь, предлагаем метод распределенной активной магнитной цепи, обоснование которой проведем на базе эквивалентного соленоида. Метод эквивалентного соленоида подразумевает использование при расчете внешнего поля постоянного магнита однослойного соленоида, имеющего бесконечно тонкую обмотку с током i с линейной плотностью тока, приходящейся на единицу длины со- леноида, принимаем равной величине намагниченности магнита M [2].

Уравнение полного тока по замкнутому пути, охватывающему обмотку однослойного соленоида, имеет вид

l

J H d l + J H dl = J Mdz

L2 ²     L. ¹ c     0      ,     (4)

где L₁ – участок пути интегрирования, проходящего внутри соленоида, L₂ – участок пути интегрирования, проходящего вне соленоида. В левой части (4): H₂ – напряженность магнитного поля соленоида (или магнита) вне соленоида (или вне магнита); H_1с=B₁ / µ ₀– напряженность поля внутри соленоида; H₁ – напряженность поля внутри магнита; B₁ – индукция внутри соленоида или магнита. В правой части (4): l– длина ПМ; M– намагниченность, являющаяся функцией напряженности поля внутри магнита.

Вводим систему координат 0-z вдоль оси симметрии соленоида, начало которой поместим в нейтральном сечении соленоида. При переходе к величинам, характеризующим магнитное состояние магнитной цепи, усредним внутреннее поле соленоида в каждом нормальном сечении z :

< B 1 >= S S B 1 (r,z)dS   < M >= S S M ( r,z)dS . ₍₅₎

Аксиальный магнитный поток в сечении z будет определяться формулой Ф(z) = 〈 B₁ 〉 S и подчиняться уравнению непрерывности Ф(z) = Ф(0) – Ф_S(z) . Здесь: Ф(0) = – магнитный поток в нейтральном сечении соленоида; Ф_S(z) – поток рассеяния через часть боковой поверхности соленоида, расположенной между нейтральным сечением и сечением в точке z ; S – площадь поперечного сечения соленоида (магнита).

Для перехода к распределенной магнитной цепи выбираем пару зеркально расположенных элементарных соленоидов длиной dz , т.е. отстоящих на одинаковое расстояние z от начала координат в обе стороны координатной оси, рис. 2. Составим уравнения полных токов для каждого элементарного соленоида по таким замкнутым путям, охватывающим элементарные обмотки, которые прилегают к бесконечно тонким поверхностям этих обмоток:

dU–2 + dU–1С = dF–, dU2 + dU1С = dF, (6) где dU–2 , dU2 – падения магнитных напряжений по путям, прилегающим к наружной поверхности обмотки соленоида, соответственно для левого и правого элементов; dU–1С , dU1С – падения магнитных напряжений по путям, прилегающим к внутренней поверхности обмотки соленоида, соответственно для левого и правого элементов; dF– , dF – МДС элементарных соленоидов. Учи- тывая симметрию расположения элементарных соленоидов, полагаем правомерность следующих равенств:

〈B1〉dz dU–1С = dU1С =   µ0 = r0dzФ(z);

dF–= dF = 〈M〉dz , (7) где r0 = 1/µ0S – распределенное магнитное сопротивление внутреннего пространства соленоида. Добавим для каждого элементарного соленоида уравнения непрерывности магнитных потоков, направления которых соответствуют рис. 2:

Ф(-z-dz) = Ф(-z) – dФ_S(-z) ,

Ф(z+dz) = Ф(z) – dФ_S(z) ,        (8)

где dФS(z) – приращение потока рассеяния через боковую поверхность элементарного соленоида. При этом между каждыми двумя зеркально расположенными элементарными участками поверхности соленоида существует паритет меж- ду приращениями потоков рассеяния, заключающийся в том, что в силу симметрии магнита выходящий с левой стороны элементарный поток dФS(z) равен входящему с правой стороны элементарному потоку dФS(-z). Поэтому этот элементарный поток рассеяния можно выразить по закону Ома dФS(z) = dФS(-z) =dGSU2(z) .     (9)

Здесь: dGS =gSdz и gS – соответственно магнитная проводимость и распределенная магнит- ная проводимость пространства, по которому замыкается магнитный поток dФS(z); U2(z) =2ϕ2(z) – разность магнитных потенциалов между дву- мя зеркально расположенными элементарными участками внешней поверхности соленоида, где ϕ2(z) – магнитный потенциал на внешней поверхности соленоида (магнита) на расстоянии z от нейтрального сечения, в котором ϕ2(z=0)=0

Подставляя в (8) формулу (9) и учитывая следующие выражения для дифференциалов магнитного потока

Ф(-z-dz) – Ф(-z) ≅ _dz dz ,

Ф(z+dz) – Ф(z) ≅ ddФz dz, получаем первое уравнение дляz описания распределенной магнитной цепи эквивалентного соленоида dФ dz

= – g_SU₂ .

В соответствии с рис. 2 разность магнитных напряжений между точками -z-dz и z+dz и соответственно между точками -z и z будет равна

U₂(z+dz) – U₂(z) = dU_–2 + dU₂ .     (11)

Выражая приращения магнитных напряжений следующим образом dU [U2(z+dz)– U2(z)]≅ dz2 dz ,

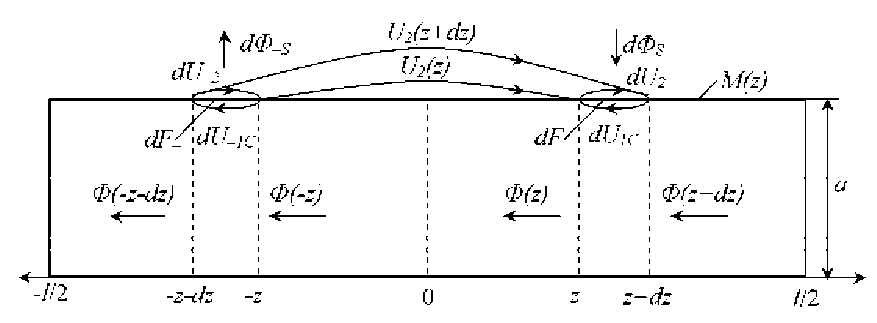
Рис. 2. Структура распределения магнитных напряжений по поверхности обмоток элементарных соленоидов и между элементарными соленоидами

приводим (11) к виду

dU

² dz =dU + dU .

_dz           –2     2

Подставляя в (12) dU_–2 и dU₂ из (6) с учетом (7), получаем второе уравнение для описания активной распределенной магнитной цепи эквивалентного соленоида

dU

-2Г = ² <  M > ^{- 2 Г} 0 Ф .

Величина М на каждом элементарном участке магнита является функцией значения Н в теле магнита. Выразим эту зависимость через В . Для этого, преобразуем характеристику размагничивания материала (1) к следующему виду

B

H= (– Br 1)HCB и, подставляя в (2), имеем

M ( B ) = B - BH CB- + ^H CB. ^ц 0     B r

Подставляя (14) в (13) и учитывая первое уравнение в (7), получаем линейное уравнение для описания активной распределенной магнитной цепи эквивалентного соленоида

dU 2 dz

= 2(H CB – r М Ф) ,

ной системе уравнений и схеме распределения напряжений на рис. 2 будет соответствовать магнитная схема замещения элементарного звена (рис. 3,а) короткозамкнутой распределенной магнитной цепи (рис. 3,б). Магнитное состояние на выходе распределенной линии ( z=l /2) соответствует магнитному состоянию на полюсах магнита, поэтому к выходным зажимам цепи присоединено магнитное сопротивление внешней среды R , так как магнитный поток магнита замыкается через внешнюю среду.

В работе [5], исходя из условия линейности магнитного потенциала на поверхности, определена математическая модель распределенной магнитной проводимости по воздуху gl , которую обозначим gS0 . Эта проводимость не зависит от магнитного режима и однородна. В сепараторах каждый магнит окружен сложной средой в виде слоеного пирога с различными магнитными про-ницаемостями, поэтому будем применять следующую математическую модель распределенной магнитной проводимости gs= gso ЦэФ, (16) где цЭФ - эффективная относительная магнитная проницаемость внешней многослойной среды.

Таким образом, система уравнений (10) и (15) линейна и с постоянными коэффициентами, поэтому приводим к одному неоднородному обыкновенному уравнению

где r_М = H_CB / B _r S , – распределенное магнитное сопротивление постоянного магнита.

Таким образом, полученная система уравнений (10) и (15) включает в себя параметры материала и параметры постоянного магнита, и устанавливает связь между такими величинами, которые характеризуют магнитное состояние магнита. Это падение магнитного напряжения на внешней поверхности соленоида U₂(z) , совпадающее с падением напряжением на поверхности магнита, и магнитный поток Ф(z) . При этом дан-

d2Ф dz2

^^^^^^^в

Y ²Ф = ^- 2g s ^H CB ,     (17)

где Y = 2r^rgg s . Используем граничные условия при z = 0: U₂(0) = 0, Ф(z=0) = Ф(0) . Тогда решения (17) и (10) в точке z = l /2 (на выходе рас-

пределенной магнитной цепи) соответственно

принимают вид

Ф(2 ) =

H_CB r M

+

Ф(0) - H CB r_M

, Yl ch2, (18)

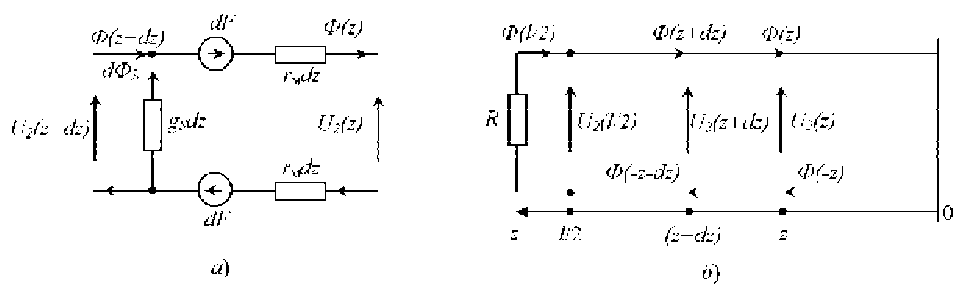
Рис. 3. Распределенные активные магнитные схемы замещения: а ) элементарного звена магнита; б ) магнита в целом в виде длинной линии

U 2 (l ⁾ = g! ^[ Ф⁽⁰⁾ - HT J shT (19)

Э Y 2 .

Формулы (18)-(19) выражают магнитное состояние постоянного магнита цилиндрической формы между его полюсами с учетом потока рассеяния через боковую поверхность магнита. При изменении магнитного потока в нейтральном сечении Ф(0) система уравнений (18)-(19) будет описывать вебер-амперную характеристику магнита. Так как внешняя среда моделируется магнитным сопротивлением R через которое проходит магнитный поток (18) вследствие приложенного напряжение (19) (рис. 3, б), то из уравнения, выражающего закон Ома,

2r ^ML ^[ ф (0) _ H CB 1 sh ^Y = 2H CB +^[ ф (0) _ H CB "I c _h I I 1 N g s L p M J 2 [ r_M L p Г м J 2 J можно вычислить рабочий магнитный поток в нейтральном сечении магнита – Ф_р(0).

Применяя к линейной распределенной цепи метод эквивалентного генератора (ЭГ), приходим к двухэлементной схеме замещения магнита (рис. 4) с параметрами: FЭ – МДС генератора; RМЭ – внутреннее магнитное сопротивление. Параметры ЭГ определяем традиционным способом, вычислением на выходных зажимах распределенной цепи напряжения холостого хода

U2x(l) и магнитного потока короткого замы-2 l кания Фк(2) . Из (18) следует, что режим холостого хода возникает при выполнении условия

Ф x (0) = H_CB ( 1 - ( ch у ) ¹ ) / Г м , которое, подставляя в (19), дает

U 2X (|) = - 2^ th 4 .     (20)

Знак “–” указывает на то, что верхний вывод распределенной схемы на рис. 3,б соответствует южному магнитному полюсу. Величина МДС будет равна

Из (19) следует, что режим короткого замыкания возникает при выполнении условия Ф_К(0) _ H c _B / Г м = 0 , которое, подставляется в (18), дает ^ф к ( 2 ) = ^hcb / г_м . Внутреннее магнитное сопротивление генератора будет равно

U 2X(2 ) = 2r M _th Y l

^RМЭ = Фl(L\ ^{Y 2} . ^{(22) K(} 2 )

В приближении нулевого потока рассеяния через боковую поверхность положим g_S = 0 , тогда из (21) и (22) будет F_Э = F = H_CBl и R_МЭ= R_М= r_Мl соответственно, что и следовало ожидать. В этом случае схема ЭГ выражает такую внешнюю вебер-амперную характеристику, которая соответствует характеристике размагничивания материала (1).

Если магнит находится в равномерном внешнем магнитном поле с напряженностью H₀ , тогда магнитная характеристика на каждом элементарном участке описывается уравнением размагничивания материала (3) и, соответственно, М(В) принимает вид

M ( B ) = B _ BH CB + ( H cb ± H 0 ) . (22)

Ц 0 ^В Г

Сопоставляя (22) с (14) приходим к выводу, в формулах (15), (17)-(21) следует заменить Н _СВ на Н _СВ ± H₀ . Знак “–”, если H₀ размагничивающее поле, знак “+”, если H₀ намагничивающее поле

Пассивную неоднородную среду сепаратора будем замещать совокупностью магнитных проводимостей (или сопротивлений) по методу сеток [8], когда все пространство сепаратора разбивается на такие элементарные объемы, в пределах которых магнитный поток можно считать квазипостоянным и квазиоднородным. В общем случае элементарный объем предполагает форму параллелепипеда,

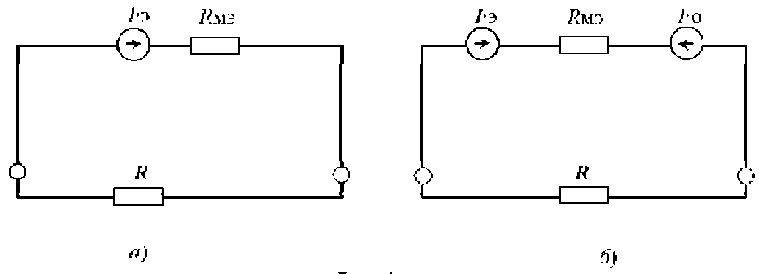
Рис. 4. Магнитная схема замещения постоянного магнита

вырезанного из сплошной среды, который замещается шестью сопротивлениями. Если поле обладает симметрией, например, цилиндрической симметрией, то элементарные объемы могут иметь форму цилиндрических слоев и т.п.

ЗАКЛЮЧЕНИЕ

Для оптимизации магнитных сепараторов, выполненных на постоянных магнитах, предлагается использовать метод магнитных цепей, который подразумевает эквивалентную замену физического пространства сепаратора совокупностью магнитных источников и магнитных сопротивлений (проводимостей). Для реализации этого подхода разработаны эффективные магнитные схемы замещения постоянного магнита, учитывающие поток рассеяния, обоснована связь параметров схем замещения со справочными параметрами материала магнита и даны рекомендации при воздействии на магнит внешнего поля.

Исследования выполнены при финансовой поддержке Министерства образования и науки

РФ по аналитической ведомственной целевой программе “Развитие научного потенциала высшей школы (2009 – 2010 годы)” на 2009 год, регистрационный номер 2.1.2/4506.