Оптимизация механизмов безопасности в рамках протокола IPSec

Все IP-пакеты (входящие и исходящие) сопоставляются с упорядоченным набором правил политики безопасности. При сопоставлении используется фигурирующий в каждом правиле селектор – совокупность анализируемых полей сетевого уровня и более высоких протокольных уровней.

Системы, реализующие IPsec , функционируют как межсетевые экраны, фильтруя и преобразуя потоки данных на основе предварительно заданной политики безопасности [1].

Протокольный контекст безопасности в IPsec – это однонаправленное соединение (от источника к получателю), предоставляющее обслуживаемым потокам данных набор защитных сервисов в рамках одного протокола ( AH или ESp ). В случае симметричного взаимодействия партнерам придется организовать два контекста (по одному в каждом направлении). Если используются AH и ESp , потребуется четыре контекста.

Протокольный контекст создается на базе управляющего с использованием ключевого материала и средств аутентификации и шифрования последнего. Протокольные контексты являются средством проведения в жизнь политики безопасности. Политика безопасности должна быть задана для каждого сетевого интерфейса с задействованными средствами IPsec и для каждого направления потоков данных (входя-щие/исходящие). Согласно спецификациям IPsec , политика рассчитывается на бесконтекстную (независимую) обработку IP-пакетов.

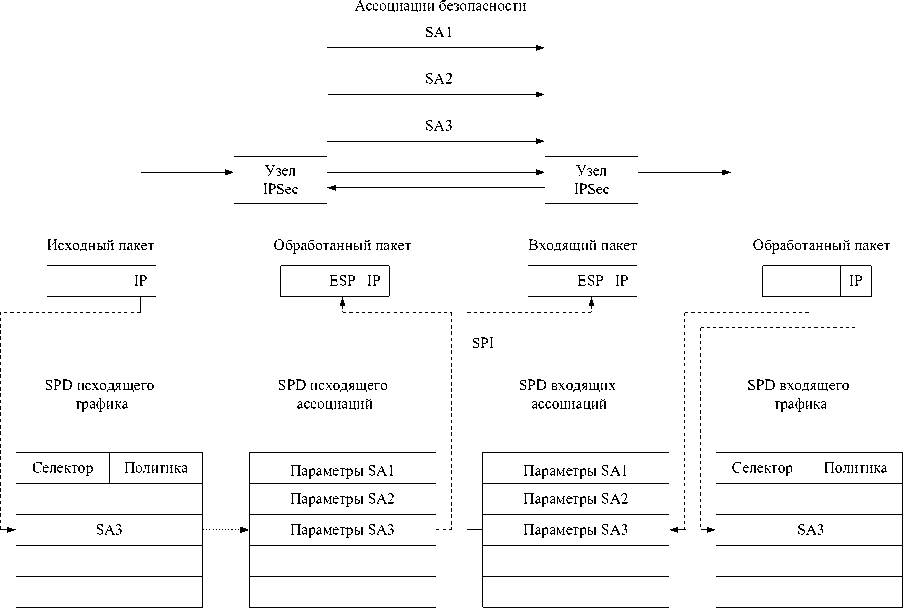
Рис. 1. Установление соответствия между IP-пакетами и правилами их обработки

База данных политики безопасности (SpD) представляет собой упорядоченный набор правил. Каждое правило задается как пара:

• •    совокупность селекторов ;

• •    совокупность протокольных контекстов безопасности .

Селекторы служат для отбора пакетов, контексты задают требуемую обработку. Если правило ссылается на несуществующий контекст, оно должно содержать достаточную информацию для его (контекста) динамического создания. Очевидно, в этом случае требуется поддержка автоматического управления контекстами и ключами. В принципе функционирование системы может начинаться с задания базы SpD при пустой базе контекстов ( SAD ); последняя будет наполняться по мере необходимости.

Дифференцированность политики безопасности определяется селекторами, употребленными в правилах. Обработка исходящего и входящего трафика не является симметричной. Для исходящих пакетов просматривается база SpD, находится подходящее правило, извлекаются ассоциированные с ним протокольные контексты и применяются соответствующие механизмы безопасности. Во входящих пакетах для каждого защитного протокола уже проставлено значение SpI, однозначно определяющее контекст. Просмотр базы SpD в таком случае не требуется; можно считать, что политика безопасности учитывалась при формировании соответствующего контекста.

Сложность процесса формирования механизмов безопасности приводит к большим затруднениям в выборе и поддержании оптимальных режимов работы в рамках протокола IPsec . Эти трудности обусловлены многообразием факторов, их сложной взаимозависимостью, наличием неконтролируемых возмущений.

Методы оптимизации могут быть различными в зависимости от конкретной формулировки задачи, объема и качества исходной информации, выбранных критериев оптимальности. Среди методов, получивших наибольшее распространение в промышленной оптимизации, достойное место занимает последовательный симплексный метод поиска и его модификации из-за их простоты и эффективности при поиске в сложных условиях.

Сущность симплексных методов состоит в том, что в k -мерном пространстве управляемых переменных x i движение к оптимуму осуществляется последовательным отражением вершин симплекса. Симплекс представляет собой фигуру с k +1 вершинами, не принадлежащими ни одному пространству меньшей размерности. В случае k =1 – это прямая, при k =2 – треугольник, k =3 тетраэдр и т.д. Целевая функция вычисляется в каждой из вершин симплекса. При поиске максимума вершина с наименьшим значением целевой функции отбрасывается и строится новый симплекс. Направление последнего перемещения симплекса в факторном пространстве достаточно близко к направлению градиента линейного приближения целевой функции.

На разных этапах ставятся различные задачи оптимизации, например, для этапа восхождения – максимум математического ожидания смещения центра симплекса к цели, а на этапе доводки – достижение заданной точности. Характер оптимизации во время доводки обусловлен расстоянием до цели: при малых расстояниях симплекс в среднем удаляется от точки экстремума целевой функции, при больших – приближается к этой точке. Поэтому локальные характеристики процесса доводки зависят от расстояния до цели и для изучения движения симплекса, представляющего собой случайное блуждание в районе цели, применяются интегральные статистические характеристики поиска. Условное математическое ожидание смещение центра симплекса к цели зависит от соотношения расстояния ρ до цели и длины шага λ. Для каждого значения отношения полезного сигнала А, определяемого как произведение L |grad Q| (L – длина ребра симплекса) к среднеквадратичному отклонению помехи δ при заданных λ и κ существует расстояние ρ = R , при котором М [λ /ρ] =0. Величина R называется радиусом стационарной орбиты, к которой в среднем тяготеет центр симплекса, блуждая вокруг цели. Радиусу R соответствует относительный радиус стационарной орбиты S=R /λ, позволяющий анализировать влияние параметров поиска на точность отыскания экстремума.

Локальная плотность распределения перехода центра симплекса любой ориентации из состояния ^ в состояние q представляется в виде [2]

fs («©= j¹ p j ) 5 [q-(l ; + *)].

AJ где Pj мм) — вероятность отражения j-й вершины; 5 - дельта-функция; gj - значение величины А при отражении j-й вершины.

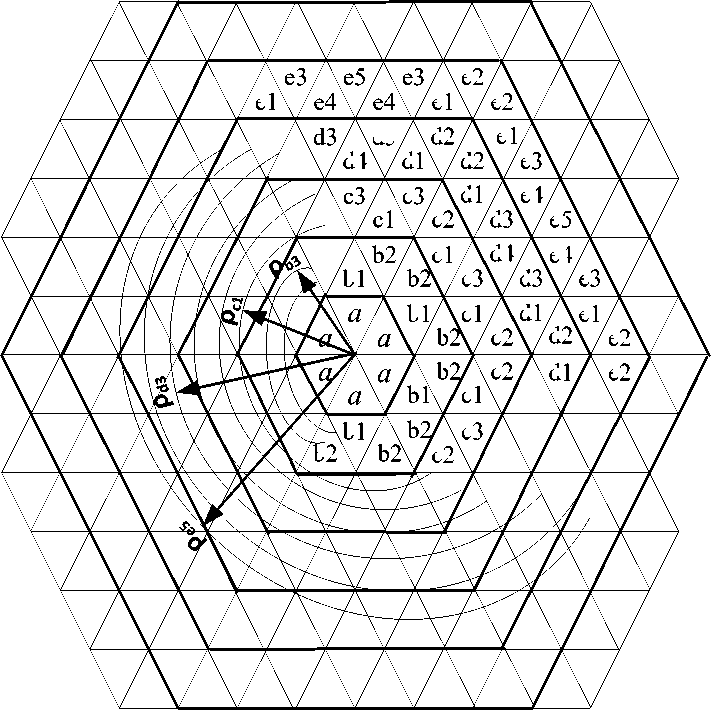
Каждый шаг поиска вблизи экстремума зависит как от ориентации симплекса, так и от расстояния его центра до цели. Состоянием системы а , Ь 1 , Ь 2 , с 1 , с₂, с₃, d 1 . соответствуют расстояния до цели р_а 1 , р_{Ь 1} , Р ь₂ , Р_{С 1} , Р с₂ , Р с 3 Р а 1 ,. (рис. 2). Относительному радиусу S стационарной орбиты R блуждания симплекса вокруг экстремума соответствует определенное минимальное количество шагов поиска достижения цели при условии, что длина ребра симплекса постоянная. Так состояния системы a соответствует 0–й орбите, состояния системы Ь 1 , Ь₂ - 1-й орбите и т.д. Последовательность простых состояний а, Ь_ъ Ь₂,. образуют сложные состояния системы при построении многосвязной марковской цепи. В [2] показано, что в результате синтеза структуры марковской цепи, описывающей процесс поиска на этапе доводки, оптимальным будет алгоритм со свободным отражением. Данный алгоритм является базовым для оптимизации переходных вероятностей при поиске с распознаванием состояний.

Оптимизация переходных вероятностей осуществляется введением в алгоритм симплексного поиска правила распознавания состояний.

'1 при (m j <к + 2) 2 при (m j < к + 2) 3 при (m j < к + 2) Л при (m j > к + 2)

^ ^(у п - ^y n-q — ^0);

^ ^(у п    У п-q ^{— 0)};

^ ^(у п    У п-q < ⁰⁾;

^ ^(у п    ^y n-q < ⁰⁾<

где mj - число последовательных шагов поиска, в ходе которых вершина с номером j - не отражалась ; j=1,.,k+1 ; у_п - значение измеряемой величины в вершине симплекса V n ; q - глубина предыстории.

e1

b1

b1

b2

c3

c2

e2

e1

e2

d4

c1

e4

d3

c3

e3

d2

e1

d4

d1

d2

e3

d1

e4

c3

d3

c2

e5

d1

b1

c1

e1

a d2

b c2

e2

a

b c2

d1

e2

a c1

a

Рис. 2. Блуждание симплекса вблизи экстремума

d3

Данное правило позволяет в случае удаления симплекса от цели исключить переходы, связывающие состояния марковской цепи (рис. 3) 2→6, 6→17, 17→27, 7→13, 13→18, 22→28, 30→24, 20→14, 14 → 8, 31^21, 21^9, 9^4 (т.е. P 26 =0, P₆ , ₁₇ =0,. P₉₄ =0).

Приведем основные правила алгоритма симплексного поиска с распознанием состояний, полученные в результате оптимизации переходных вероятностей стохастического графа, описывающего процесс блуждания симплекса вокруг экстремума.

• 1.    Из всех вершин симплекса выбрать вершину V_r с наименьшим значением у .

• 2.    Присвоить m=z .

• 3.    Оценить состояние на данном шаге поиска согласно (2):

• а)    если z=1,4, перейти к п. 4.

• б)    если z=2,3, перейти к п. 7.

• 4.    Отразить вершину с номером m относительно противоположной грани симплекса.

• 5.    Определить значение у ^ ) во вновь полученной вершине.

• 6.    Перейти к п. 1.

• 7.    Из всех вершин симплекса, кроме V_r, выбрать вершину V_P с наименьшим значением у.

• 8.    Присвоить m=P .

• 9.    Перейти к п. 4.

Приведенные правила процесса поиска на этапе доводки назовем алгоритмом симплексного поиска с запретом прямолинейного движения.

При определении переходных вероятностей используется методика, рассмотренная в [2], однако в данном случае необходимо учитывать величину полезного сигнала в соответствии с ориентацией симплекса.

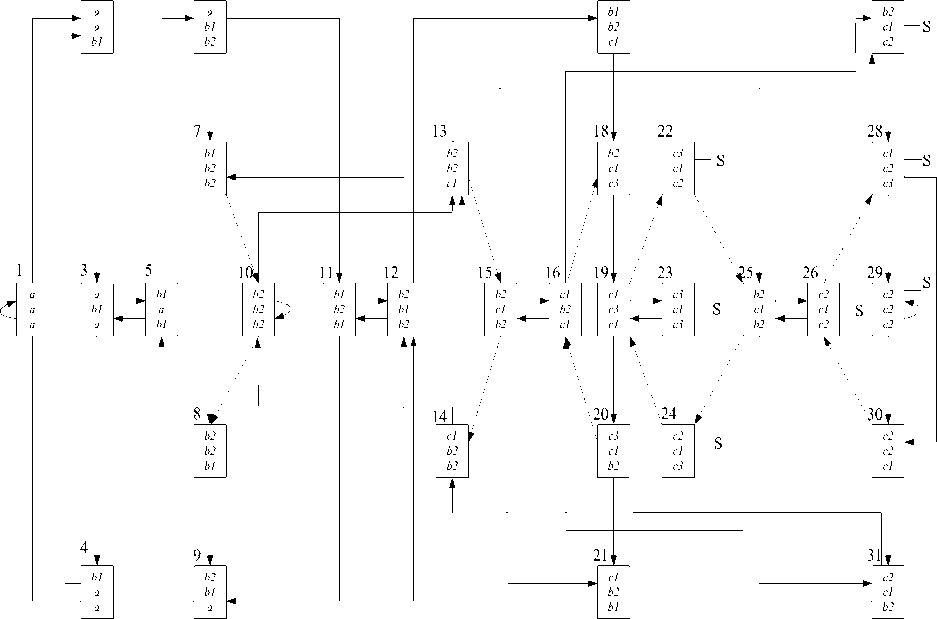
Рис. 3. Граф стохастического блуждания симплекса вокруг экстремума

Предельные вероятности простых состояний a, Ь 1 , Ь 2 , с 1 , с₂, с₃ определяем путем суммирования вероятностей сложных состояний, имеющих одинаковые последние состояния:

Р_а=Р 1 +Р з +Р 4 +Р д .

^Pb1 = ^P2^+P5^+PS^+P11^+P21 , ^Pb₂ = ^P6 ^+P7 ^+P10^+P12 ^+P14^+P15^+P20^+P2 7^+P31 , P_C 1 =P 13 +P 16 +P 17 +P 19 +P 25 +P 30 .

P C2 =P 22 +P 26 +P 2_S +P 29 , ^pc₃ = ^pia^+p23^+p24 -

На основе вероятностей (3) получаем предельную плотность вероятности нахождения центра симплекса на орбите R:

fs(V — Pa8(^ -  )+ P_b8tf - %)+ P_c5tf - *),

AAA

где

Pb = Pbi + Pb2 ,     Pc = Pci + PC2 + Рез , n _ Pbi+Pb2    „ _PC1+Pc2+Pc3

Pb — —;—, Pc —---;---■

Характеристика (4) позволяет оценить точность доводки, определить вероятность того, что в процессе случайного блуждания в районе цели симплекс не выйдет из заданной области.

Сопоставление зависимости плотности распределения fs (ξ) для алгоритмов со свободным отражением вершин, запретом возврата и запретом прямолинейного движения показывает, что применение алгоритма с запретом прямолинейного движения можно в 1,2 ^ 1,3 раза повысить точность оптимизации, поддерживать оптимальный режим работы протокола IPsec в рамках заданной политики безопасности.