Оптимизация min-sum алгоритма декодирования LDPC-кодов

Использование современных методов цифровой обработки сигнала и помехоустойчивого кодирования значительно расширяет возможности космических систем связи. Однако реализация сложных алгоритмов требует значительных вычислительных ресурсов. В настоящее время широкое распространение получили ПЛИС (программируемые логические интегральные схемы), которые позволяют гибко реализовывать ресурсоёмкие алгоритмы и использовать возможности параллельной обработки информации.

Цель данной работы – исследовать возможность улучшения характеристик min-sum LDPC-декодера с помощью нормализующих коэффициентов с возможностью реализации на ПЛИС, а также показать методы вычисления коэффициентов для заданного кода.

2.    Алгоритм с нормализацией проверочных метрик

Для декодирования LDPC-кодов применяются как декодеры с «мягким», так и с «жёстким» решением. Декодеры с мягким решением более эффективны, т.к. получают больше информации, но при этом сложнее в реализации. Одним из наиболее эффективных алгоритмов декодирования низкоплотностных кодов является алгоритм «распространения доверия» («belief-propagation»). В реализации декодера (далее – sum-product алгоритм), на входе которого используются llr-значения бит (llr – log-likelihood ratio – логарифмический коэффициент правдоподобия), метрики узлов переменных vi,j инициализируются значениями llr априорной вероятности, вычисленными из принятых демодулятором значений Yi,а метрики проверочных узлов для каждой итерации декодирования вычисляются как

C n,m = 2 * tanh ^-1 П   tanh( v m ) .

^j = ^N m,n \ n

А обновлённые значения v i_,j получают через данные от проверочных узлов:

v m,n

= llr _n +

E

c j,m .

j = N m,n \ m

На каждой итерации вычисляются апостериорные значения llr каждого бита, т.н. «мягкий выход».

Подобные вычисления при реализации декодера на ПЛИС требуют много ресурсов для реализации функций tanh ^-1 и tanh (обычно реализуется в виде чтения из памяти заранее вычисленных значений), поэтому широкое распространение среди аппаратных реализаций получил алгоритм декодирования min-sum, в котором используется приближенное вычисление проверочных метрик, где основной является операция вычисления минимума вектора метрик узлов переменных, которая требует гораздо меньше ресурсов ПЛИС и позволяет использовать вычисления с большей разрядностью данных (таблицы 16 битных значений предварительно вычисленных функций должны занимать ~ 1Мбит памяти):

^с П,т = ^min( v N m,n \ n,m ) *   П sign ⁽ v j,m ) ‘                      ⁽³⁾

j = N m,n \ n

Благодаря такой замене функции вычисления метрик алгоритм min-sum нечувствителен к линейному масштабированию входных данных, что также упрощает приёмник благодаря отсутствию необходимости измерять значение дисперсии шума, которое входит в формулу вычисления llr как масштабирующий коэффициент. Для рассматриваемого кода из [1] с длиной кодового слова 2048 бит и кодовой скоростью r = 2 получаем проигрыш эффективности исправления ошибок ~ 1 дБ по отношению к значениям BER, указанным в [1].

Покажем, что проверочные метрики алгоритма min-sum всегда больше по абсолютному значению метрик sum-product алгоритма. Очевидно, что

| tanh x \ <  1

и а из (1) следует

получим, что

\ tanh x 1 \ <  \ tanh x 2 \ О \ x 1 \ <  \ x 2 \ ,

| tanh c nm I

tanh( ^{v j} ₂ ^,m )

j = N m,n \ n

\ c n,m \ <  ^{min 1} v N m,„ \ n,m ¹ ,

¹ c n,m ¹ — \ c n,m \ .

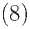
3.    Вычисление коэффициента нормализации

Таким образом, удобно применить нормализацию метрик для получения значений, более близких к sum-product алгоритму. В работе [2] для получения более точных значений метрик предлагается использовать коэффициент нормализации cf = -^j^|, заданный как отношение значений математического ожидания c и c’ соответственно. Нормализованные метрики вычисляются умножением на масштабирующий коэффициент cf:

c n,m    c n,m * cf ^.

Реализаиция на ПЛИС умножения на коэффициент требует использования дополнительных умножителей либо использования операции сложения и сдвига, если коэффициент имеет короткую запись в двоичном виде [3, 4].

На рис. 1 показаны зависимости разности метрик проверочных узлов | c ^z | — | c | ( cf = 1) и | c" | — | c | ( cf = 0 , 702) как функций двух аргументов v 1 и v 2 , вычисленные методом Монте-Карло с выбором равномерного распределения значений аргументов.

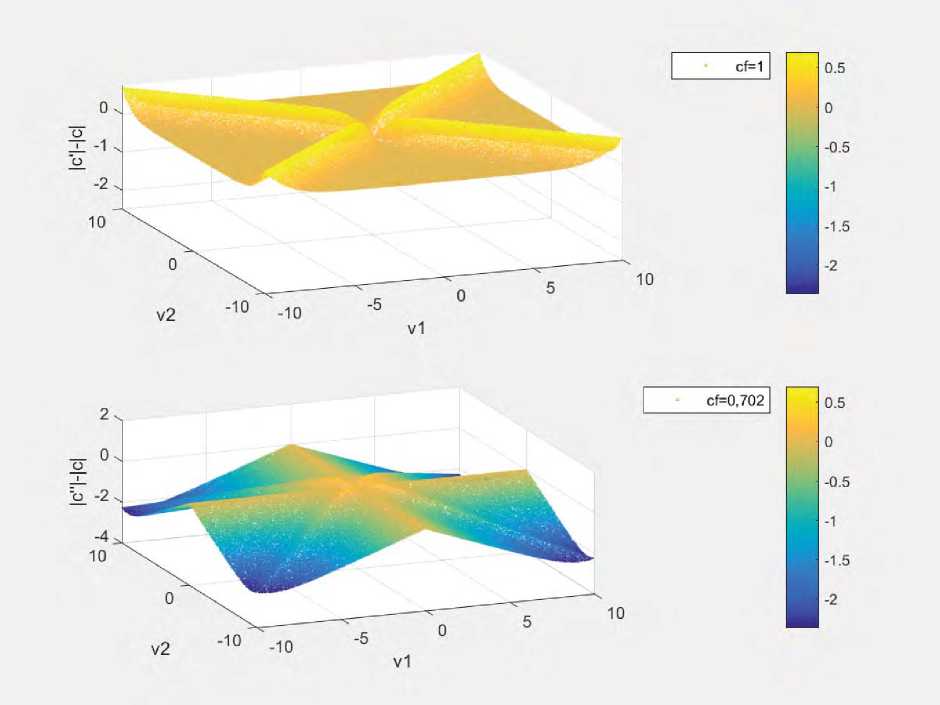
Рис. 1. Ошибка вычисления метрики проверочных узлов

Однако, хотя использование теоретически вычисленного значения улучшает эффективность алгоритма min-sum, можно получить лучшее значение коэффициента в результате симуляций методом Монте-Карло или минимизацией функции с одним параметром, т.к. нормализация среднего значения [2] не означает отсутствие потерь эффективности исправления ошибок. Для поиска оптимального значения коэффициента была написана программа в среде MATLAB, использующая оператор fminsearch для поиска минимума функции, вычисляющей количество неисправленных ошибок декодером, с различными значениями коэффициента cf. Для поиска минимума MATLAB использует метод Нелдера–Мида [5], также известный как метод деформируемого многогранника и симплекс-метод, — метод безусловной оптимизации функции от нескольких переменных, не использующий производной (точнее — градиентов) функции, а поэтому легко применим к негладким и/или зашумлённым функциям. Для моделирования был сгенерирован набор тестовых векторов информации и шума с Nb = 1.5 дБ (больший уровень шума вносит слишком много ошибок для нормальной работы канала, слишком маленький уровень шума ведёт к резкому уменьшению числа ошибок и, как следствие, к увеличению необходимого числа тестовых фреймов для нормальной работы алгоритма поиска минимума), число тестовых пакетов – 16384 (меньшее число пакетов может вызвать эффект подстройки коэффициента к заданному вектору шума и на другом значении шума дать значительно худшую эффективность кодека).

4.    Результаты

В результате нескольких попыток вычисления коэффициента cf для различных тестовых наборов кодовых слов с наложенным шумом (использовалась сигнальная конструкция QPSK и декодер с максимальным числом итераций 50) были получены несколько значений cf ~ 0 , 702 и для дальнейшего моделирования было выбрано именно это значение коэффициента (в работе [2] для этого значения шума cf =0 , 61). Эффективность оптимизированного кодека в результате моделирования на большем числе пакетов и различных значениях уровня шума приведена на рис. 2, где для различных декодеров показана вероятность битовой и пакетной ошибок. Также для сравнения приведена эффективность JPL-декодера от авторов стандарта [1] (точные характеристики алгоритма и число итераций неизвестно).

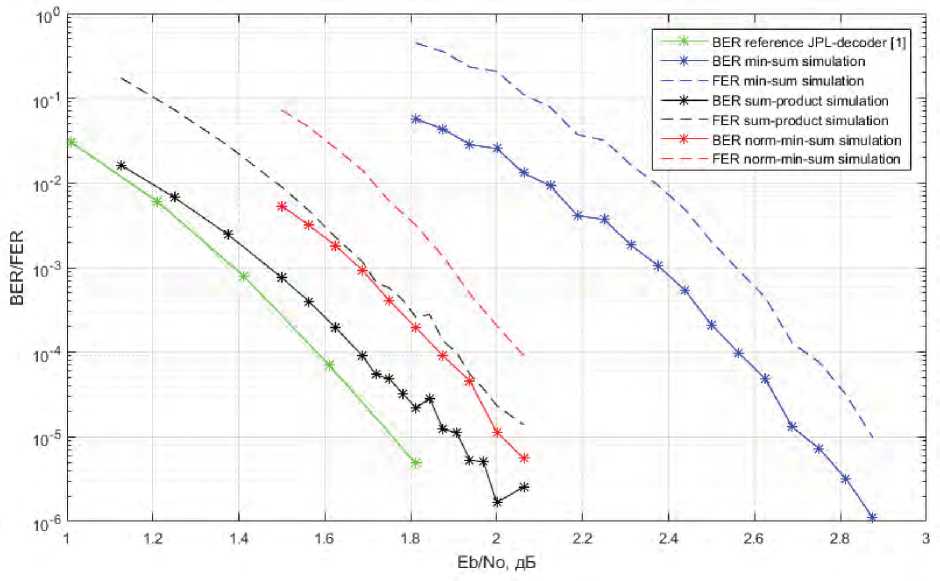
Рис. 2. Вероятность битовой (BER) и кадровой (FER) ошибки для различных декодеров

На основании результатов моделирования можно сделать вывод, что декодер с оптимизированными вычислениями проверочных метрик значительно ближе по эффективности к sum-product декодеру и проигрывает ему всего ~ 0 . 2 дБ, против ~ 0 . 9 дБ потерь у minsum декодера. В качестве предмета дальнейших исследований предлагается рассмотреть возможность адаптивной подстройки коэффициента cf для разных значений _N ^{E b} в канале.