Оптимизация многослойного теплозащитного экрана солнечного зонда

СалоСина м.о.

Исследования Солнца и околосолнечного пространства представляют интерес для понимания физических процессов, вызывающих наиболее мощные проявления солнечной активности, связанные с солнечной короной и солнечным ветром [1].

В настоящее время в России разрабатывается проект «Интергелио-Зонд», в рамках которого должен быть создан космический аппарат (КА) для гелиофизических исследований в ближайшей окрестности Солнца. Планируемая дата запуска — после 2025 г. [2]. Главным разработчиком КА «Интергелио-Зонд» является ФГУП «НПО им. С.А. Лавочкина». Программа исследований включает изучение динамики солнечной атмосферы и параметров солнечного ветра, вспышек на Солнце, магнитных полей в его полярных областях и формирование солнечного цикла [1]. Схема полета КА «Интергелио-Зонд» обеспечивает сближение с Солнцем на расстояние 60…70 солнечных радиусов в результате серии гравитационных маневров у Венеры [1]. Наклонение этой орбиты составит 17...18° [3]. Последующие гравитационные маневры приведут к увеличению наклонения орбиты до 30,5° и радиуса перигелия до 110 солнечных радиусов [3]. Достаточно большое наклонение финальной орбиты КА «Интергелио-Зонд» к плоскости эклиптики дает возможность исследовать приполярные области Солнца, являющиеся источником высокоскоростного солнечного ветра [1].

Исследование Солнца с гелиоцентрических орбит с низким перигелием предполагается провести также в проекте NASA Solar Probe Plus (планируемая дата запуска с 31 июля по 19 августа 2018 г.) [4] и европейском проекте Solar Orbiter (дата запуска — октябрь 2018 г.) [5], научные задачи которых аналогичны задачам российского проекта. В проекте NASA предполагается вывести КА на гелиоцентрические орбиты с беспрецедентно низким радиусом перигелия, равным 9,5 радиусов Солнца (~6,6 млн км) [6]. Наклонение орбиты КА Solar Probe Plus не превысит 3,5° [6].

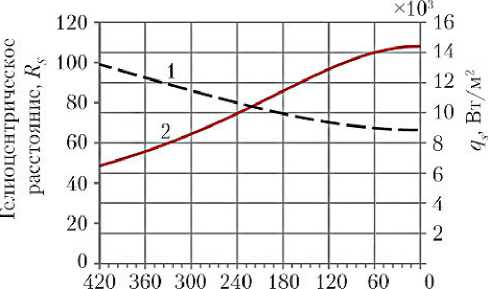
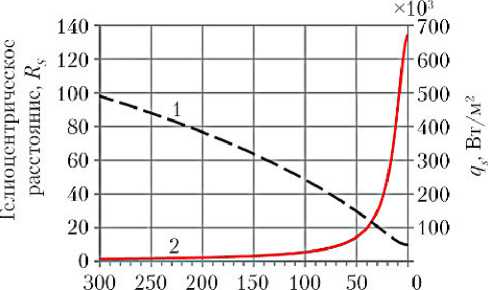
Конструкции и системы, входящие в состав солнечных зондов, подвергаются высокоинтенсивному радиационному тепловому воздействию, определяемому траекторией КА. Рис. 1 иллюстрирует зависимость гелиоцентрического расстояния 1 и плотности теплового потока солнечного излучения 2 , воздействующего на внешнюю поверхность экрана КА, от времени до прохождения перигелия для двух вариантов орбит, параметры которых в первом случае (рис. 1, а ) приняты близкими параметрам орбиты КА «Интергелио-Зонд» (радиус перигелия 66,4 R_s ; радиус афелия 0,885 а. е.; период 168,523 сут [3]); а во втором случае (рис. 1, б ) — параметрам орбиты КА Solar Probe Plus (радиус перигелия 9,736 R_s ; радиус афелия 0,763 а. е.; период 93,762 сут).

Обеспечение требуемых тепловых режимов является одной из наиболее сложных проблем, возникающих при проектировании подобных систем. От практического решения задач выбора концепции тепловой защиты, высокотемпературных теплостойких материалов конструкции солнечного зонда и теплозащиты его научного модуля, учета влияния продуктов уноса на постановку и проведение научных экспериментов во многом зависит успешное выполнение научных задач миссии и возможность реализации проекта в целом.

Требуемый тепловой режим КА в ближайшей окрестности Солнца будет обеспечиваться за счет применения специальных экранов, защищающих КА от воздействия высокоинтенсивного потока прямого солнечного излучения, жестких требований к ориентации КА относительно Солнца, организации регулируемого отвода тепла.

Время до прохождения перигелия, ч

а)

Время до прохождения перигелия, ч

б)

Рис. 1. Зависимость гелиоцентрического расстояния (1) и плотности теплового потока солнечного излучения, воздействующего на внешнюю поверхность экрана КА (2), от времени до прохождения перигелия: а — орбита «Интергелио-Зонд»; б — орбита Solar Probe Plus

В проекте «Интергелио-Зонд» теплозащитный экран состоит из внешнего и внутреннего экранов, соединенных между собой при помощи центрального и внешнего шпангоутов и профилей [7]. Тыльная поверхность внутреннего экрана закрывается многослойной экранно-вакуумной теплоизоляцией (ЭВТИ). Экраны, соединяющие их шпангоуты и профили, а также элементы крепления на внешней стороне изготавливаются из термостойкого углеродуглеродного композиционного материала (УУКМ) «Углекон» [7].

Теплозащитный экран солнечного зонда Solar Probe Plus , разработанный компанией The Johns Hopkins University Applied Physics Laboratory ( Laurel, Maryland, USA ), представляет собой многослойную конструкцию, состоящую из слоя высокопористого ячеистого материала на основе стеклоуглерода толщиной ~11 см [8], расположенного между слоями углерод-углеродного материала толщиной ~0,076 см [6].

На внешнюю сторону экрана нанесено покрытие A1 2 O 3 ( A s /е ~0,6) [6]. Тепловой поток от тыльной стороны теплозащитного экрана КА к модулю служебных подсистем не превышает 50 Вт [6]. Максимальная температура внешней поверхности экрана КА, достигаемая в перигелии орбиты, составляет 1 650 K [6].

Основным конструктивным элементом теплозащитного экрана КА Solar Orbiter является композитная панель, состоящая из двух слоев углепластика, между которыми расположен сотовый заполнитель из алюминиевого сплава (рис. 2). На обращенной к Солнцу стороне панели с помощью десяти звездообразных элементов крепления из титанового сплава Ti6Al4V устанавливается высокотемпературная многослойная ЭВТИ, состоящая из внешнего, внутреннего и шести промежуточных слоев титановой фольги, толщины которых составляют, соответственно, 50, 25 и 10 мкм [5]. Для предотвращения контакта титановые экраны высокотемпературной ЭВТИ формованы рельефом. На внешний слой высокотемпературной ЭВТИ наносится покрытие ( A s / е ~1,1) [5]. Для обеспечения теплового режима композитной панели, рабочая температура которой ограничена диапазоном 130..160 °C, панель полностью закрывается многослойной ЭВТИ, состоящей из 20 слоев алюминизированной с двух сторон рифленой полиимидной пленки [5]. Конструкция теплозащитного экрана обеспечивает выполнение заданных ограничений на допустимые радиационный и кондуктивный тепловые потоки к КА ≤30 и ≤15 Вт, соответственно, и допустимую температуру панели КА <50 °C [5]. Максимальная температура внешней поверхности высокотемпературной ЭВТИ, достигаемая в перигелии орбиты КА, составляет 522 °C. Экран изготовлен компанией Airbus Defense &  Space ( Stevenage, UK ) совместно с TAS-I ( Turin, Italy ).

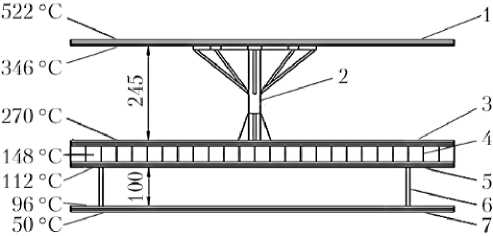
Рис. 2. Схема теплозащитного экрана КА Solar Orbiter: 1 — высокотемпературная ЭВТИ; 2 — опора; 3 — ЭВТИ (20 слоев); 4 — композитная панель; 5 — ЭВТИ (20 слоев); 6 — элемент крепления; 7 — ЭВТИ на панели КА. Слева указаны приведенные в работе [5] максимальные температуры элементов конструкции экрана в перигелии орбиты

Примечание. ЭВТИ — экранно-вакуумная теплоизоляция.

материалы для многослойноготеплозащитного экрана солнечного зонда

Материалы, входящие в состав теплозащитного экрана солнечного зонда, должны обладать высокими удельными механическими свойствами — прочностью, жесткостью, стойкостью к вибрации и воздействию факторов космического пространства при рабочих температурах 120…2 000 K, иметь высокую температуру плавления и низкий коэффициент термического расширения. К основным требованиям, определяющим возможность эксплуатации конструкции, относится низкая скорость сублимации материалов в вакууме, необходимая для минимизации плотности собственной внешней атмосферы КА и ее влияния на работу научной и служебной аппаратуры. Перспективными для использования в конструкции теплозащитного экрана солнечного зонда являются углерод-углеродные композиционные материалы («КМ-ВМ», «Десна Т-1», «Десна-4», «КМ-ВМ-4D», «Граурис», IMT, Aerolor-32, Sepcarb I, II и др. [9]), изготавливаемые на основе тканых углеродных наполнителей и углеродной матрицы. Данные материалы сохраняют стабильные свойства, структуру, форму и размеры изделий при нагревании в неокисляющей среде вплоть до 2 000 К, легко поддаются механической обработке, обеспечивая возможность изготовления элементов конструкции практически любой формы и размеров, и обладают такими уникальными свойствами, как невысокая плотность, регулируемая пористость, высокий коэффициент черноты, стойкость к механическим и термическим ударным нагрузкам, повышение прочности при нагревании до 2 500 K. Механические и теплофизические характеристики углерод- углеродных композиционных материалов определяются схемой армирования, видом матрицы и технологией изготовления.

Технические характеристики углерод-углеродных композиционных материалов [9, 10]: плотность                     1,3…2 г/см3;

прочность при растяжении   70…370 МПа;

прочность при сжатии прочность при изгибе ударная вязкость модуль упругости теплопроводность интегральная полусферическая степень черноты

110…200 МПа;

130…550 МПа;

50…100 КДж/м2;

20…200 ГПа;

3,2…150 Вт/(м·К);

0,502…0,904 [11].

Скорость испарения углеродных материалов в вакууме можно оценить по формуле [11]:

lgro = A - B/T, где го — скорость испарения, г/(см2-с); A и B — коэффициенты (A = 9,072; В = 36 650); T — температура. Скорость испарения графита при температуре 2 000 °С составляет 1,15·10–8 г/(см2·с) [11]. Повышению стойкости углеродных материалов и улучшению оптических характеристик их поверхности способствуют нанесение защитных покрытий (Al2O3; ZrO2; HfO2 и т. д.) и объемная пропитка жидким кремнием или жидкими металлами (например, сплавами Zr-5%Nb или Hf-20%Ta) [12].

Дальнейшее улучшение механических и оптических свойств углерод-углеродных композиционных материалов связано с заменой углеродной матрицы на керамическую. Примером таких материалов являются углерод-карбидные материалы («Гравимол», «Карбосил», Sepcarbinox [9] и др.), получаемые путем пропитки углеродного каркаса двух- или трехмерной структуры карбидами кремния, титана, циркония, ниобия, гафния или сложными карбидами.

Технические характеристики углеродкарбидных материалов [9]:

плотность 1,7…2,8 г/см3; прочность при растяжении 100…200 МПа; прочность при сжатии 90…300 МПа; прочность при сдвиге 35…60 МПа; модуль упругости 23…250 ГПа; коэффициент термического расширения (1…5)·10–6 K–1;

теплопроводность 9,8…25 Вт/(м·К).

Наряду с углерод-углеродными и углерод-карбидными композиционными материалами в конструкции теплозащитного экрана солнечного зонда могут быть использованы керамические теплозащитные материалы, которые успешно применялись для тепловой защиты пилотируемых космических кораблей многоразового использования. Примерами подобных материалов являются разработанные для воздушнокосмической системы Space Shuttle анизотропные теплозащитные материалы:

• •    LI-2200 (кажущаяся плотность 352 кг/м³; прочность при изгибе 1 300 кПа в поперечном и 500 кПа в продольном направлении; состав: волокна кварцевого стекла диаметром 0,5…12,0 мкм [13]);

• •    FRCI-12-22 (кажущаяся плотность 228 кг/м³; прочность при изгибе 1 800 кПа в поперечном и 650 кПа в продольном

направлении; состав: 22% волокон алюмо-боросиликатного стекла диаметром 12 мкм ( Nextel 312) и 78% волокон кварцевого стекла диаметром 1,4 мкм ( Astroquartz ) [13]);

• •    HTP-6-22, HTP-12-22, HTP-12-35, HTP-16-22 (кажущаяся плотность 70…270 кг/м³; прочность при изгибе 800…2 800 кПа; состав: волокна Al₂O₃ диаметром 3 мкм и волокна кварцевого стекла диаметром 1,4 мкм [13]);

• •    AETB-12-20, AETB-15-30 (кажущаяся плотность 170 кг/м³; прочность при изгибе 1 000 кПа; состав: волокна кварцевого стекла, боросиликатного стекла и Al₂O₃ [13]).

Для тепловой защиты воздушно-космической системы «Буран» отечественной промышленностью были созданы аналогичные материалы на основе сверхчистого аморфного кварцевого волокна ТЗМК-10, ТЗМК-25 с плотностями 140 и 255 кг/м3, соответственно (по данным производителя — АО «ОНПП «Технология» им. А.Г. Ромашина»).

Применение кварцевых теплозащитных материалов ограничено температурой 1 530 K. Материалы, состоящие из волокон SiO2 и Al2O3, могут использоваться до температуры 1 700 K [13].

На основе керамических материалов разрабатывается и более стойкая тепловая защита, температура применения может достигать 1 970 К [13]. В ее состав входит высокопористый слой волокнистой теплоизоляции или спеченной пенокерамики, защищенный слоем SiC или Si3N4 в виде облицовки, воспринимающей основную тепловую и механическую нагрузку. В качестве теплоизоляционного слоя могут использоваться пористые керамические материалы из Al2O3 и ZrO2, рабочие температуры которых могут достигать 1 750 и 2 200 °С, соответственно, в вакууме при отсутствии нагрузки и термических ударов.

Скорость испарения плотных керамических материалов в вакууме при 2 000 °С составляет ~10–6…10–7 г/(см2·с) [11].

Большими потенциальными возможностями для изготовления теплоизоляции обладают пористые композиционные материалы, в которых в качестве наполнителя используются заранее изготовленные пустотелые микросферы [14]. Такие материалы характеризуются малой теплопроводностью в сочетании с высокой удельной прочностью на сжатие, устойчивостью к деформации и низкой кажущейся плотностью. Весьма перспективны материалы на основе углеродных микросфер, связующими в которых служат пироуглерод или пенообразующие смолы.

Технические характеристики  карбо низированного пеноматериала на основе углеродных микросфер [14]: плотность                    0,05…1 г/см3;

прочность при сжатии       0,5…49,0 МПа;

рабочая температура в нейтральной и восстановительной средах    до 3 000 °С.

Перспективными для использования в конструкции теплозащитного экрана солнечного зонда являются высокопористые ячеистые материалы на основе стеклоуглерода с пористостью 82…98%. Материалы обладают высокой жесткостью, достаточной прочностью (0,3…4,0 МПа) в диапазоне рабочих температур, малой плотностью (50…400 кг/м3), невысокой теплопроводностью (0,06…0,60 Вт/(м·К)) [9]. Теплоизоляционные свойства данных материалов значительно ухудшаются при высоких температурах в связи с существенным возрастанием в их пространственной сетчатой структуре доли радиационного теплопереноса. Указанный недостаток можно устранить, заполнив материал углеродным аэрогелем, обладающим высокой твердостью, жаропрочностью, чрезвычайно низкими плотностью (0,07 г/см3) и теплопроводностью (менее 1 Вт/(м^К) при 1 900 °С) [15].

проектирование многослойного теплозащитного экрана солнечного зонда

При проектировании многослойного теплозащитного экрана солнечного зонда возникает проблема выбора оптимальных проектных параметров, удовлетворяющих заданному допустимому тепловому состоянию защищаемого объекта и минимизирующих критерий оптимальности. В большинстве случаев постановка задачи подразумевает определение толщин слоев, обеспечивающих минимум удельной массы покрытия при соблюдении заданных ограничений на максимальные температуры в слоях.

Предполагается, что процесс распространения тепла в многослойном покрытии, состоящем из L слоев различных материалов толщиной dl и плотностью р l, l = 1, 2, …, L, является одномерным по пространственной координате, и поле температуры в l-ом слое T((x, т), l = 1, 2, ..., L, где т — время, описывается обобщенным квазилинейным уравнением теплопроводности. Поскольку для материалов, входящих в состав теплозащитно- го экрана солнечного зонда, характерен высокий уровень рабочих темпера- тур, оказывающих сильное влияние на их теплофизические свойства, необходимо учитывать зависимость коэффициентов параболических уравнений Cl, λl, l = 1, 2, …, L, от температуры.

Теплоперенос в системе описывается следующей системой дифференциальных уравнений:

д T

д T

C(T)    l l      дτ

д         д T

λ( T )     ^l ; x ∈ ( X , X );

дx    l      дx           l–1

l = 1, 2, …, L; τ ∈ (τmin, τmax];(1)

Tl(x, τmin) = T0l; x ∈ [Xl – 1, Xl]; l = 1, 2, …, L.(2)

На внутренней границе могут быть заданы граничные условия I или II-го рода:

д T ( X , τ)

– β₁λ₁( T ₁( X ₀, τ))     ¹д x ⁰    + α₁ T ₁( X ₀, τ) = q ₁(τ);

τ ∈ (τ_min, τ_max].                   (3)

Условие теплообмена на внешней границе, учитывающее тепловой поток, излучаемый нагретой поверхностью экрана, можно представить в виде:

д T ( X , τ)

–λ _L ( T_L ( X_L , τ))     ^L д _x ^L    = – q_R (τ) + q _изл;

τ ∈ (τ_min, τ_max],              (4)

где q_R (τ) = A_sq_s (τ) — плотность радиационного теплового потока; A_s — поглощательная способность материала; q_s = S ₀ / L ² — плотность теплового потока солнечного излучения; S ₀ = 1 398 Вт/м² — солнечная постоянная для Земли; L — расстояние от КА до Солнца в а. е., определяемое формой и размером орбиты; q _изл = εσ T ⁴ — тепловой поток, излучаемый нагретой поверхностью экрана; ε — интегральная полусферическая степень черноты.

Контактный теплообмен между слоями характеризуется контактными термическими сопротивлениями R_l, l = 1, 2, …, L –1, также являющимися функциями температуры:

λ _l ( T_l ( X_l , τ))

д T(X_t , т ) дx

= λ l +1 ( T l +1 ( X l , τ))

^д W X ■ т )

дx     ’

l = 1, 2, ..., L – 1; τ ∈ (τ_min, τ_max];       (5)

д T ( X , τ)

X , ( T , (X, т)) R , ( T(X, , т)) —-- T ( X, , т) -

– T l + 1 ( X l , τ); l = 1, 2, ..., L – 1; τ ∈ (τ min , τ max ].      (6)

Искомый вектор толщин слоев d должен обеспечить минимум массы единицы площади поверхности покрытия, которая определяется функцией:

L

J ( d ) = ∑ρ _l ( d_l – d_{l –1}) = ^–ρ ^T d l = 1

при ограничениях dl > 0; l = 1, 2, …, L; T(Xl, τ) ≤ T llim;

l = 1, 2, …, L ; τ ∈ (τ min , τ max ],              (7)

где T _l ^l _im — значения предельно допустимых температур на границах слоев ( X_l , l = 1, 2, …, L ).

Для определения толщин слоев многослойного теплозащитного экрана в данной работе использовалась вычислительная схема, сочетающая в себе метод штрафной функции [16] и метод спроектированного лагранжиана [17]. Первый из них, характеризуемый большой областью сходимости, применяется в качестве средства поиска хорошего начального приближения для метода спроектированного лагранжиана, обладающего отличными свойствами локальной сходимости.

Учитывая, что к ограничению d_l > 0; l = 1, 2, …, L неприменимы функции внешней точки, в качестве штрафной функции удобно использовать обратную барьерную функцию, обеспечивающую приближенное решение задачи (7) внутри допустимой области. При этом вспомогательная функция, минимизируемая при фиксированном значении параметра штрафа, имеет вид:

1               1

P( d, ) J

l - d(     i - P.(w)

где T_i — ограничения на температуру границ слоев, которые в результате конечноразностной аппроксимации краевой задачи (1)–(6) на сетке с N_j узлами по времени представляются в виде:

T = T ^l – T ( X , τ); l = 1, 2, …, L ; j = 1, 2, …, N .

i lim       l ^, j      ^{,,,       ,,,} j

Вспомогательная функция (8) минимизируется до тех пор, пока два последовательных значения Pk и Pk+1 не стан–ут такими, что |(P – P )/P | < ε и r P(d ) < ε, ,      – k         k+1      k                 k k           , где P(dk) — функция штрафа; ε — наперед заданное значение погрешности решения задачи. Найденное таким образом приближение оптимального решения задачи затем уточняется методом спроектированного лагранжиана с квадратичной подзадачей.

Согласно данно–му методу, в искомой оптимальной точке d* достигается минимум функции Лагранжа L(d, Ψ) = J(d) – ΨTT (ΨT — вектор множителей Лагранжа; T–(d–)T = {T 1 – T(X , τ ), …, T l – T(X, τ )} — lim               1, 1 , , lim               l, Nj вектор ограничений) на множестве векторов, орто–гональных градиентам активных в точке d* ограничений [18]. В дальнейшем t-мерный вектор, составленный –из значений функций активных– в точке d* ограничений, обозначается T , а матрица их градиентов — A.

Очередное приближение оптимального вектора проектных параметров вычисляется как d–i+1 = d–i + gi–pi, где gi — длина шага вдоль направления –pi.

Направление ^– pⁱ определяется как решение подзадачи, целевая функция которой представляет собой квадратичную аппроксимацию функции Лагранжа, а система ограничений определяет множество точек, в которых равна нулю линейная ап_–прок-симация нелинейных ограничений T [17]. Квадратичная подзадача имеет вид:

найти minΦ _L ( d )             (9)

при ограничениях A ( d )^– p ≤ – T ,

где Φ = ^– g^{T –} p +    ^– p^TH ^– p — квадратичная

L ₂

аппроксимация функции Лагранжа;

^– g = grad J ( d ) –_– A ( d ) ^T Ψ — градиент функции Лагранжа; A ( d ) —_– матрица градиентов, активных в точке d ограничений; H — приближение матрицы Гессе функции Лагранжа.

Система ограничений подзадачи (9_–) получена путе_–м разложения функции T в окрестности d в ряд Тейлора:

T(d*) = T(d, Xl, τj) + A(d)(–p) + o(|| –p|| 2) = 0, где –p = d* – d.

Пренебрегая нелинейным слагаемым, получаем систему ограничений (10).

Оптимальный для квадратичной подзадачи (9) вектор ^– p выражается через матрицы Y и Z , первая из которых состоит из _– векторов базиса ранг-пространства A ( d ), а вторая — из базисных векторов его ортогонального дополнения: ^– p = Y ^– p_y + Z ^– p_z .

Для допустимого вектора ^– p имеем

AY ^– p_y = – T ^–.                (11)

Составляющая ^– p_y , найденная из ограничений (11), будет одинаковой у всех допустимых векторов ^– p , отличаться они будут только составляющими ^– p_z , значения которых ничем не ограничены. Вектор ^– p_z должен доставлять безусловный минимум квадратичной аппроксимации функции Лагранжа Φ _L и может быть найден из системы:

Z^THZ ^– p_z = – Z^T (^– g + HY ^– p_y ).

Очередное приближение вектора множителей Лагранжа определяется из

H ^– p + ^– g = A^{T –}Ψ ^T.

Значение длины шага g ⁱ определяется как приближенное решение задачи одномерной безусловной минимизации функции Лагранжа.

Найденная точка считается оптимальной, если выполнены следующие условия:

y p II - < s;

(1 + II d II)

__________________ II Z^Tg\\            _< ^

(1 + max(l + \^J( d)\, || g _F ( d )ID)    ’

|Tj | ≤ δ, где ε — наперед заданное значение погрешности решения задачи оптимизации; δ — заданное значение пог–решности выполнения ограничений; –gF(d) — вектор, составленный из компонент градиента функции Лагранжа, соответствующих свободным переменным.

В качестве методического примера решена задача выбора толщин плоского двухслойного теплозащитного экрана (рис. 3), внешний обращенный к Солнцу слой которого изготовлен из УУКМ, а внутренний — из высокопористого ячеистого углеродного материала (ВПЯУ). Теплофизические характеристики материалов [19–22], используемые в расчетах, представлены в таблице.

Предполагается, что на экран воздействует внешний радиационный тепловой поток плотностью 600 000 Вт/м2. Собственные тепловыделения КА малы и в расчетах не учитываются. Оптические характеристики покрытия внешней поверхности As = 0,33; ε = 0,47. Интегральная полусферическая степень черноты ВПЯУ составляет 0,63. Допустимая температура тыльной поверхности экрана принималась равной 350 К, температура на границе слоев теплозащитного покрытия ограничивалась значением 1 650 К. Оптимальные толщины слоев УУКМ и ВПЯУ, полученные при данных условиях с округлением до целых, равны 1 и 156 мм, соответственно. Температура внешней поверхности экрана 1 651 K. Масса единицы площади поверхности покрытия составляет 9,24 кг.

теплофизические характеристики материалов

Материал		УУКМ	ВПЯУ
Плотность, кг/м3		1 440	50
Я ^ я о ^ 43 я я g о й 8 о 3 ^ Я й £ m	300	4,91	0,02
	500	6,96	0,05
	700	7,22	0,09
	900	7,24	0,14
	1 100	7,37	0,19
	1 300	7,45	0,27
	1 500	7,66	0,36
	1700	7,92	0,49
и о г , у ^ § Я « "В S ^ о	300	981	34,77
	500	1 771	52,20
	700	2 184	64,94
	900	2 440	71,49
	1 100	2 592	74,65
	1 300	2 683	73,36
	1 500	2 757	80,25
	1 700	2 821	80,06

Примечание. УУКМ — углерод-углеродный композиционный материал; ВПЯУ — высокопористый ячеистый углеродный материал.

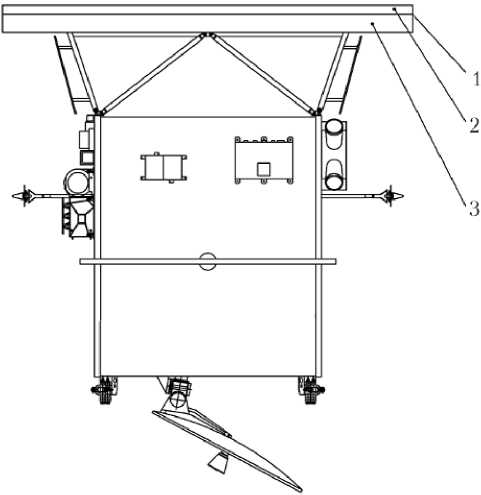
Рис. 3. Схема проектируемого теплозащитного экрана: 1 — теплозащитный экран; 2 — 1-й слой (УУКМ); 3 — 2-й слой (ВПЯУ) Примечание. См. табл.

Оптимальные толщины слоев УУКМ и ВПЯУ, рассчитанные в предположении, что на экран воздействует тепловой поток плотностью 15 000 Вт/м2, а остальные условия задачи остаются прежними, равны 1 и 27 мм, соответственно. При этом температура между слоями не превышает 640 K, а масса единицы площади поверхности покрытия составляет 2,79 кг.

заключение

Полученные результаты подтверждают работоспособность и эффективность представленной вычислительной схемы, сочетающей методы штрафной функции и спроектированного лагранжиана с квадратичной подзадачей. Первый из них обладает большой областью сходимости и обеспечивает нахождение начального, приближенного решения внутри области, удовлетворяющей заданным ограничениям. Полученное приближение искомого решения затем уточняется быстро сходящимся методом спроектированного лагранжиана. Возможности применения предложенного алгоритма не исчерпываются решением конкретной задачи выбора оптимальных толщин слоев многослойного теплозащитного экрана солнечного зонда, рассмотренной в данной работе. Данный метод может быть использован для расчета широкого круга теплозащитных покрытий, функционирующих в условиях высокоинтенсивных нестационарных тепловых нагрузок.