Оптимизация одного класса управляемых нелинейных систем на конечном отрезке времени
Автор: Мурзабеков Заинелхриет Нугманович, Мурзабеков Асан Заинелхриетович
Журнал: Проблемы информатики @problem-info
Рубрика: Теоретическая информатика
Статья в выпуске: 3 (15), 2012 года.
Бесплатный доступ
Рассматривается задача оптимального управления нестационарными нелинейными системами с закрепленными концами траекторий. Получен алгоритм управления для одного класса нелинейных систем с ограничениями на управления на конечном отрезке времени.
Задача оптимального управления, дифференциальные уравнения, метод множителей лагранжа, нелинейная система, функционал
Короткий адрес: https://sciup.org/14320134
IDR: 14320134
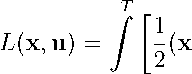
Список литературы Оптимизация одного класса управляемых нелинейных систем на конечном отрезке времени
- Атанс М. Оптимальное управление. Введение в теорию и приложения/М. Атанс, П. Фалб. М.: Машиностроение, 1968.
- Понтрягин Л. С.} Математическая теория оптимальных процессов/Л.~С.~Понтрягин, В.~Г.~Болтянский, Р.~В.~Гамкрелидзе, Е.~Ф.~Мищенко. М.: Наука, 1976.
- Беллман Р.} Динамическое программирование и современная теория управления/Р.~Бел\-лман, Р.~Калаба. М.: Наука, 1968.
- Куржанский А.~Б.} Дифференциальные уравнения в задачах синтеза управлений//Дифференц. уравнения. 2005. Т.~41, \No~1. С. 12-22.
- Мурзабеков З.~Н.} Достаточные условия оптимальности динамических систем управления с закрепленными концами//Мат. журн. 2004. \No~2. С. 52-59.
- Мурзабеков З.~Н.} Конструктивный метод решения краевых задач оптимального управления для линейных нестационарных управляемых систем при наличии внешних воздействий и ограничений на управления//Докл. НАН РК. Сер. физ.-мат. 2009. \No~3. С. 16-21.
Статья научная
