Оптимизация основных параметров коническо-цилиндрического редуктора

Основная задача при проектировании зубчатых редукторов – разработка конструктивных условий формирования параметров ступеней и передаточного отношения каждой ступени. Разбивка общего передаточного отношения редуктора зависит от требований, которые предъявляются к данной конструкции.

Критериями оптимизации наиболее часто выступают следующие:

• –    стоимость конструкции;

• –    минимальные габаритные размеры;

• –    минимальная масса;

• –    минимальный приведенный момент инерции редуктора;

• –    минимальная кинематическая погрешность редуктора.

Рассмотрим методику определения оптимальных параметров коническо-цилиндрического редуктора. Основным условием работоспособности редуктора является условие контактной прочности колес, которое одновременно предусматривает минимальную массу. Поэтому металлоемкость и стоимость редуктора будут зависеть от габаритных размеров редуктора: длины L ; высоты H ; ширины B .

Необходимо учитывать, что на величину оптимального передаточного отношения ступени оказывают непосредственное влияние такие параметры, как коэффициент ширины зубчатого венца цилиндрической передачи – ψ _ba , коэффициент ширины зубчатого венца конической передачи – ψ _{b Re}, контактное напряжение колес –

[ a H ]. Поэтому выбор достаточно обоснованных значений параметров коническо-цилиндрических редукторов – задача довольно сложная.

Длина коническо-цилиндрического редуктора определяется по следующей зависимости (рис. 1):

С учетом принятых обозначений и формул выражение

(1) после соответствующих преобразований примет вид

L — а о

a ₁

■ (2 i 34 + 1) ,

L ^— d e 2 + A w 34 + - w -, (1)

где d_{e 2} – внешний делительный диаметр колеса конической передачи; A_{w 34} – межосевое расстояние цилиндрической передачи; d_{w 4} – диаметр делительной окружности колеса цилиндрической передачи.

где a ₀

T ■ i общ ■ ^п 12

\   ^[° H ^] 24

a 1 ^— K d

K H в34 ■ ⁿ34 a 2 ^— K a • 3

ψ ba

.

H β12 ⁱ общ

V b Re ■ S °² ■ (1 - 0,5 ■ V b Re ) ²

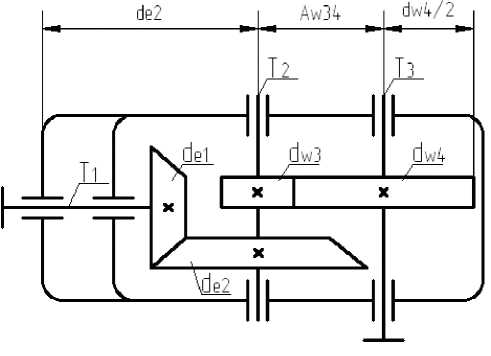
Рис. 1. Коническо-цилиндрический редуктор

Эта зависимость показывает, что длина редуктора зависит от разбивки передаточного отношения по ступеням. Из анализа уравнения (5) видно, что минимальная длина редуктора L будет при i ₃₄ равному

a1 + a 2 i34 — a2

.

Таким образом, на величину оптимальной разбивки

передаточного отношения оказывают влияние соотношение S _a , параметры ^ _ba и ^ b Re . При изменении ширины колес и материалов каждый раз меняются передаточные отношения ступеней и, следовательно, длина редуктора. Оценить это влияние можно с помощью разработанной автором программы «Система автоматизированного проектирования электромеханического привода. Проек-

По условию контактной прочности зубчатых колес межосевое расстояние цилиндрической передачи и внешний делительный диаметр колеса конической передачи определяется по следующим формулам:

T ' KHB34

A w 34 - K a ( i 34 + 1) 3---- 3 И 234 2 ,        (2)

V ba ■ ^[ ° H ] ₃₄ ■ i 34

где K_а – коэффициент зависящий от свойств материала и типа передачи; T ₃ – момент на валу Т ₃; K_{H в34} – коэффициент неравномерности распределения нагрузки по ширине венца цилиндрической передачи; i ₃₄ – передаточное отношение цилиндрической передачи; ^ ba - коэффициент ширины зубчатого венца по межосевому расстоянию цилиндрической передачи; [ a _H ]₃₄ - допускаемое контактное напряжение колеса цилиндрической передачи;

d e 2 ^— K d ^х

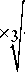
_________ T 2 ■ K H в12 ■ i 12 _________

^V b Re '[ ° H ] ₁₂ ■ ⁽¹ - 0,5 ■ ^V b Re ) 2

где K_d – коэффициент учитывающий тип передачи и свойства материала; T ₂ – момент на валу Т ₂; K_{H в12} – коэффици-

ент неравномерности распределения нагрузки по ширине

венца конической передачи, i ₁₂ – передаточное отношение конической передачи; ^ b _Re - коэффициент ширины зубчатого венца конической передачи; [ a _H ]₁₂ - допускаемое контактное напряжение колеса конической передачи.

Введем следующее обозначение для соотношений

колес ступеней:

с ₌ ^[°H ^] 12

° = [ ° H ] 34^.

тирование коническо-цилиндрического редуктора с оптимальными параметрами „САПР-9”», схема алгоритма которой приведена на рис. 2.

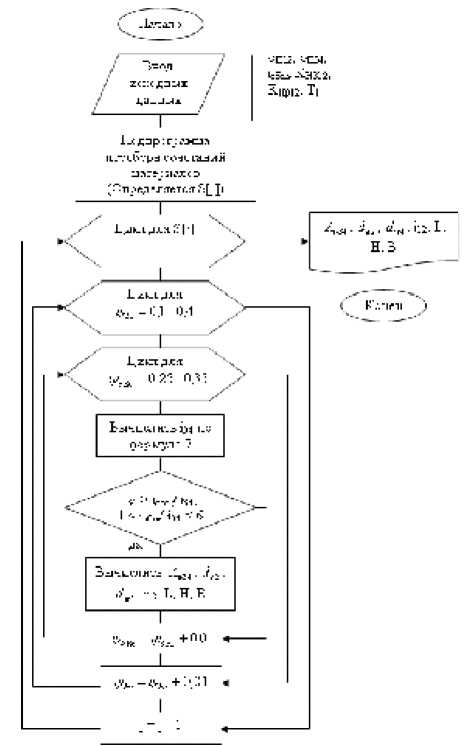
Рис. 2. Алгоритм программы

Вводимые параметры:

• –    массив материалов для колес с различными допускаемыми контактными напряжениями;

• –    общее передаточное отношение редуктора i _общ;

• –    коэффициенты неравномерности распределения нагрузки K_{H в12} и K_{H в34};

• –    крутящий момент на входе редуктора Т ₁.

Внутри программы организованны три цикла:

• –    первый цикл «Цикл для S [ j ]» – перебирает варианты сочетаний материалов, которые передаются из подпрограммы «перебора сочетаний материалов»;

• –    второй цикл «Цикл для ψ _ba = 0,1…0,4» – перебирает значения параметра в указанном диапазоне с шагом 0,01;

• –    третий цикл «Цикл для ψ _{b Re} = 0,25…0,35» – перебирает значения параметра в указанном диапазоне с шагом 0,01.

Далее все значения параметров подставляются в формулу (6) и вычисляется оптимальное значение передаточного отношения i ₃₄, проверяемые по критериям, которые указаны в блоке сравнения.

Если i ₃₄ удовлетворяет критериям, то рассчитывается L по формуле (5), H , B , A_{w 34}, d_{e 2}, d_{w 4}. Из расчетов формируется массив, из которого выбираются оптимальные варианты по L и объему внутренней полости редуктора V и выводятся на экран.

Если i ₃₄ не удовлетворяет критериям, то программа переходит к следующему своему шагу.

Анализ рассчитанных вариантов редукторов позволяет выбрать наиболее оптимальные значения параметров обеих ступеней.

K. Ya. Ivanov

OPTIMIZATION OF THE BASIC PARAMETERS OF A CONICAL-CYLINDRICAL REDUCER

The optimization of basic parameters of a conical-cylindrical reducer is considered. The methods for optimization based on the total breakdown of the gear ratio step reducer are carried out.

• А.    В. Минеев, Е. Е. Милосердов

НЕКОТОРЫЕ БАЗОВЫЕ СООТНОШЕНИЯ МОДЕЛИРОВАНИЯ ОСНОВНЫХ ПРИВОДОВ РОТОРНОГО ЭКСКАВАТОРА

Рассматриваются некоторые базовые соотношения моделирования основных приводов роторного экскаватора, приведены основные формулы, используемые в моделировании нагрузок на привод ротора в процессе экскавации породы.

Для оценки технического состояния основных функциональных узлов роторного экскаватора очень важно рассмотреть базовые соотношения основных приводов роторного экскаватора. Привод роторного колеса является одним из определяющих.

Фактическое входное погружение зубьев, режущих кромок (поясов), механизмов привода, ротора и его опорных устройств определяется величиной усилия при экскавации породы.

Нагрузка в этих элементах зависит от усилия подъема породы, массы последней в роторе и на приемно-питаю-щем устройстве, а также от массы узла ротора.

Кроме того, опорное устройство ротора нагружено центробежной силой и гироскопическим моментом, возникающим вследствие путации и прецессии валов ротора и двигателей привода. Все эти нагрузки, за исключением массы узла ротора, носят случайный или квазигармо-нический характер. При этом амплитуды их колебания весьма существенны, особенно это относится к усилию, затрачиваемому на экскавацию породы.

Структура действия сил и моментов на роторном колесе приведена на рисунке в виде схемы скоростей и усилий, действующих на кромку ковша роторного колеса.

Мощность, необходимая для резания горной массы определяется следующим образом [1]:

Pp = Fp∙Vp, где Fp – средняя составляющая статической нагрузки привода роторного колеса; Vp –линейная скорость.

Необходимая производительность в плотной массе в секунду равна

Q p 3600 ⋅ K_p ^.

V р

Момент статической нагрузки относительно оси ро- торного колеса, связанный с резанием

M = PL = Qt . Kf =   Qt . Kf p ®p Kp ■ ®p Kp ■ ®p ■ 3 600, где юр - угловая скорость вращения ротора; Kf-коэффициент удельного сопротивления резания.

С учетом силы резания получаем следующее:

M _p - F p -R _рк - KS ^ -R _рк, где S _х - суммарная площадь поперечного сечения стружек, снимаемых всеми ковшами; R _р.к –радиус роторного колеса.

Суммарная мощность на валу роторного колеса [2]

K + р ■ R

Р р = K т ( Р р + Р п ) = K T - Q T —     рк ,     (1)

Kр где Rp.к – радиус роторного колеса; KT – коэффициент трения ковшей о породу.

Приведенное выражение определяет средние теоретические значения статических нагрузок.

Мгновенные усилия на кромках ковшей и, соответ- ственно, мгновенные значения моментов на валу привода роторного колеса определяются и переменной составляющей нагрузок, связанной с неоднородностью физико-механических свойств массива, наличием крепких включений, возникновением сколов, непостоянством числа одновременно режущих кромок, различной степенью их износа.

Характеристики переменной составляющей нагрузки формируются генератором псевдослучайных чисел, с учетом частоты вращения ротора вводятся с переменным коэффициентом K _п.с в уравнение (1).

Для определения срабатывания фрикционной муфты, установленной для предотвращения перегрузок на валу приводного двигателя, включения колодочного тормоза и т. п. выполняют анализ [1]

М р ^ М р.ср.с -

При этом максимальный динамический эффект на валу ротора

М = М + ю ■ JJ ■ С . д.р.max     р.ср.м    р мм

Для определения количества добываемой горной мас сы моделируются параметры стружки h 0 = а ■ tg ■ ^,

V где tg^ = —; а - расстояние между ковшами.

V р

Мгновенная толщина среза горной массы одним ковшом моделируется одним уравнением [1]

t в = to ■ sin Рк, где to

Qt ■ Eo

60K„ ■ nz рz

Сопротивление массива резанию определяется через прочностные свойства горных масс

σ

K Fno = 12,5-р- ■ 1д(0,7ф +10 C _M).

σ сж

С учетом площадей среза и соотношений толщины и ширины стружки

^KF П1

^KF ПО

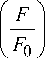
K F nz »

0,91 + 0,45 1 S + b l b S

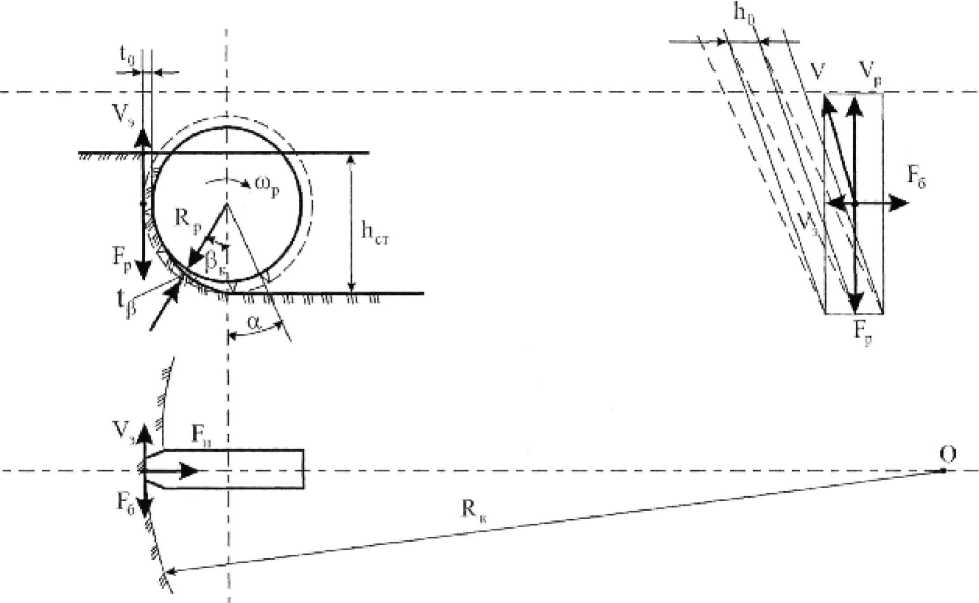
Схема усилий, действующих на кромку ковша роторного колеса:

R _к – радиус резания в горизонтальной плоскости, измеряемый по кромке ковшей; h ₀ – ширина снимаемой стружки; h _ст - высота слоя уступа; t _р - мгновенная толщина стружки, сжимаемой ковшом

CM = CK I X + — I, м к I    b / lb J где ср - временное сопротивление одностороннему растяжению в зависимости от выбранного горного массива; ссж - временное сопротивление одностороннему сжатию; b – угол внутреннего трения; Cк – сцепление в куске; X и lb - соответственно, коэффициенты структурного ослабления, средний размер элементарного структурного блока.

Фактическая производительность экскаватора определяется как [1]

Q ф = М      .

Угловая скорость вращения ротора равна [2]

ю р = ю _д - i _р.

Таким образом, при помощи данных зависимостей, моделируя условия резания грунта и факторы, влияющие на работу экскаватора, можно оптимально спроектировать привод ротора и определить мощность машины в целом.