Оптимизация параметров бинарных фазовых аксиконов для генерации терагерцовых закрученных поверхностных плазмон-поляритонов на цилиндрических проводниках

Известно, что комбинацию пучков с орбитальным угловым моментом («закрученных» пучков), распространяющихся в свободном пространстве, можно использовать для создания мультиплексного коммуникационного канала передачи данных [1, 2]. Такая возможность была продемонстрирована экспериментально в видимом [3], радиочастотном [4] и миллиметровом [5] диапазонах. При распространении в свободном пространстве дополнительным преимуществом закрученных пучков является их способность к самовосстановлению при прохождении через случайно-неоднородные среды и препятствия [6– 8], в том числе и в терагерцовом диапазоне [9]. При решении технологических задач для коммуникационных систем в свободном пространстве большую роль играют дифракционные оптические элементы (аксиконы, поляризаторы, моданы), которые позволяют формировать пучки нужного модового состава, пространственного распределения и заданной поляризации, а также позволяют кодировать и декодировать комплексные сигналы [7, 10–11].

Можно предположить, что аналогичным образом можно создать и плазмонные коммуникационные системы, передавая информацию по цилиндрическим проводникам с помощью комбинации поверхностных плазмон-поляритонов (ППП), вектор Пойнтинга которых имеет, кроме основной аксиальной составляющей, заданную азимутальную составляющую, иными словами, с помощью ППП, несущих орбитальный угловой момент (ОУМ). Для подтверждения или опровержения этого предположения необходимо провести эксперименты, которые должны подтвердить возможность генерации закрученных плазмонов, продемонстрировать сохранение их орбитального момента в процессе распространения, а также показать возможность декодирования сигнала.

Поскольку длина пробега поверхностных плазмонов видимого диапазона равна лишь десяткам микронов (см., например, обзор [12]), плазмонные мультиплексные коммуникационные устройства могут быть созданы на начальном этапе лишь в терагерцовом диапазоне, в котором длина распространения плазмонов составляет десятки сантиметров как на плоских поверхностях [13], так и на проволоках [14]. Очевидно, что закрученные плазмоны могут распространяться только по цилиндрическим проводникам. В работе [15] были предложены оптические схемы для возбуждения плазмонов на цилиндрических проводниках.

Одним из наиболее распространенных способов генерации закрученных ППП является метод дифракции излучения на краю проводника (см. работы [13, 16] и ссылки в них). В нашем случае торец цилиндра можно освещать кольцевыми пучками, сформированными с помощью дифракционных аксиконов или линз, аподизированных аксиконами. Большое разнообразие формируемых таким способом пучков продемонстрировано в работах [17– 19], а в [20] такие пучки были получены в терагерцовом диапазоне, используя излучение Новосибирского лазера на свободных электронах [21].

В настоящем сообщении приведены приближенные аналитические выражения, связывающие параметры аксиконов с радиусом цилиндрических проводников, позволяющие подобрать условия, при которых в планируемых экспериментах можно сформировать ППП с необходимым углом азимутальной закрутки. Расчеты выполнены для диапазона длин волн 8– 141 мкм, который соответствует диапазону длин волн, генерируемых Новосибирским лазером на свободных электронах.

Мы рассматриваем две конфигурации оптической системы, показанные на рис. 1 в [15]. Гауссов пучок освещает бинарный спиральный фазовый аксикон с периодом p , который формирует осесимметричный Бесселев пучок с ОУМ

E ( z , г , ф ) = E о J , ( к г )exp( k_zz + i , ф ), (1)

k = 2 π / λ= k z 2 +κ 2 , κ= 2 π / p . (2)

го по азимуту ППП нужно использовать радиально поляризованный Бесселев пучок, который можно сформировать, например, если перед аксиконом установить сегментную волновую пластинку [23].

При возбуждении плазмона собственно Бесселевым пучком может возникнуть одна проблема. Поскольку фаза соседних колец Бесселева пучка отличается на π , то при малом коэффициенте экспоненциального затухания амплитуды ППП в направлении, перпендикулярном поверхности, в область формирования электрического поля плазмона может попасть второе кольцо пучка, и интеграл перекрытия (см. выражение (7) в [15]) может оказаться малым, что снизит эффективность образования плазмона. Решением проблемы может быть использование «идеальных» ("perfect") закрученных пучков [24], представляющих собой одиночные закрученные кольцевые пучки. Установив дополнительную линзу (рис. 1 б в [15]), получим в её фокальной плоскости закрученный кольцевой пучок

Для того, чтобы реализовать обе описанные выше схемы в эксперименте, необходимо согласовать параметры аксикона, диаметр цилиндрического образца и обеспечить «закрутку» плазмона, достаточную, чтобы она была заметна на длине его распространения вдоль проводника. Вычислим угол поворота траектории вектора Пойнтинга на единицу длины оптической оси пучка для первых колец Бесселевых пучков, созданных бинарными фазовыми аксиконами. Дифференцируя правое выражение (3) и считая, что λ <  p , получим

d ф = I,k dz   2 π r ² λ^{- 2} - p ^{- 2}2 π r ² .

Угол наклона траектории вектора Пойнтинга от оси z на поверхности цилиндра радиуса r равен

Траектория вектора Пойнтинга представляет собой двухпараметрическую спираль [22]

dφ α≈r ≈ dz

,k

2 π r .

r = const,

φ=φ0 +

Iz

r ² k ² -κ ²

Нас интересует направление вектора Пойнтинга в первом максимуме Бесселевой функции, радиус которого равен

с шагом

2 π r 2 k 2 -κ 2 ,

величина которого растет для периферийных областей как r ². То есть внутренние кольца Бесселева пучка вращаются значительно быстрее внешних. Если диаметр первого кольца приблизительно равен или несколько больше диаметра цилиндра, на поверхности последнего возникнет вращающийся ППП. Поскольку электрическое поле плазмона направлено по нормали к поверхности, для возбуждения однородно-

р ( , , p ) = ( кр ) , / к = ( кр ) , p /2 п .                   (7)

Подставив значения аргумента ( кр ) , Бесселевой функции [25, С. 201], построим график (чёрные точки), показанный на рис . 1. Для дальнейших оценок достаточно аппроксимировать его линейной функцией F(E), значения которой справедливы только для целых , :

F(E) ( кр ) , « (1,244 ± 0,026) , . (8)

Тогда радиус первого максимума Бесселева пучка (7) можно аппроксимировать выражением

р ( к , E) = ^{F ( E} ) p » 0,20 k , ( p / k ),                 (9)

2π

а выражение (6) примет вид:

~ £X     0,80

^а” F ( £ ) p " ( p / X )

.

Таким образом, для угла вектора Пойнтинга относительно оптической оси для первых Бесселевых колец мы получаем в нашем приближении выражение (10), не зависящее от величины топологического заряда и с точностью до коэффициента совпадающее с классической дифракционной формулой α ~ λ / p .

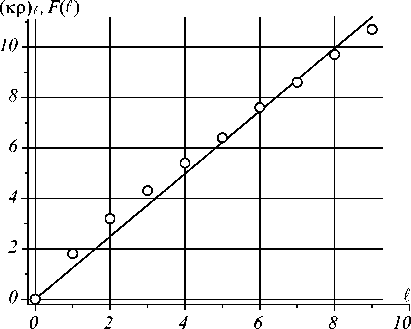
Рис. 1. Величины ( кр ) _£ (точки) и их аппроксимация F ( £ ) (прямая) как функции модуля топологического заряда £

Для запуска плазмона цилиндрический проводник следует установить на оптической оси аксикона на расстоянии, на котором полностью формируется Бесселев пучок (см. [15, 20]):

Z = ^{R 1 + R 2}      ≈ R ( p / λ ).

⁰   2tg[arcsin( λ / p )]

Здесь R 1 – внешний радиус аксикона, а R 2 – внутренний радиус (если центральная часть аксикона закрыта непрозрачным диском).

Выражения (9), (10) и (11) позволяют связать между собой радиус Бесселева пучка, угол наклона вектора Пойнтинга и расстояние, на котором формируется пучок. Все они зависят от параметра p / λ , и лишь радиус зависит еще от длины волны и величины топологического заряда £. Зависимости этих величин от отношения p / λ приведены на графике, представленном на рис. 2. Величина радиуса первого кольца Бесселева пучка приведена для длин волн 8,5 и 141 мкм и модулей топологических зарядов £ =1, 3, 9. Видно, что приемлемая величина угла наклона вектора Пойнтинга (порядка нескольких градусов) достигается при отношении p / λ ~ 4 ÷ 10. При этом для тера-герцового диапазона для больших £ радиус первого Бесселева кольца лежит вблизи одного миллиметра, а для среднего ИК – вблизи 100 мкм.

В технологических применениях гораздо удобнее воспользоваться замечательным свойством бинарных аксиконов, имеющих одинаковый период решетки p .

Для заданной длины волны λ, независимо от величины и знака топологического заряда £, мы получаем в фокальной плоскости линзы фурье-образ пучка в виде кольца одинакового радиуса, rF =f/(p/λ),

где ƒ – фокальное расстояние линзы. При этом топологический заряд кольцевого пучка идентичен топологическому заряду исходного пучка. Радиус кольцевого пучка при использовании линзы с фокусом 50 мм показан на рисунке звездочками. Он равен нескольким миллиметрам. Если желательно транспортировать ППП по цилиндру меньшего радиуса, то после захвата плазмона на торце проводника радиус последнего можно плавно уменьшить, что заодно приведет к увеличению скорости вращения ППП при сохранении величины и знака топологического заряда.

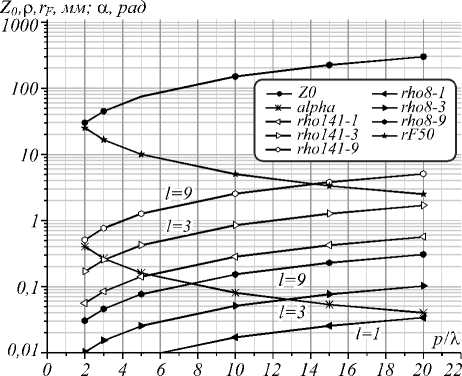
Рис. 2. Основные параметры Бесселевых пучков, сформированных с помощью спиральных фазовых аксиконов (см. выражения (9 - 12)), в зависимости от отношения периода аксикона к длине волны излучения для длин волн 141 и 8,5 мкм; £ - топологический заряд пучка

Таким образом, в настоящей работе показано, что для генерации на проволоках терагерцовых плазмонов с орбитальным угловым моментом можно использовать закрученные пучки, полученные с помощью бинарных фазовых аксиконов, которые легко изготовить с помощью фотолитографии. Графики, представленные на рис. 2, позволяют найти диапазоны параметров экспериментов по моделированию плазмонных коммуникационных систем. Сформированные ППП могут переносить ОУМ вдоль проводника, превращаясь, как было показано в [13], на конце провода в свободную волну. Если в экспериментах будет показано, что модовый состав этой волны будет отражать модовый состав излучения, сформировавшего плазмон на входе, подобно тому, как сохраняется модовый состав свободной волны, прошедшей через неоднородную среду [7], тогда будет показана возможность применения «закрученных» плазмонов для создания мультиплексных передающих линий.

Заметим в заключение, что дифракционные элементы позволяют реализовать весьма оригинальные конфигурации передающих линий. Используя метод формирования двух близко расположенных закрученных кольцевых пучков с разнонаправленной радиальной поляризацией [26, 27], можно возбуждать плазмоны на торце тонкостенного полого цилиндра [28]. Продемонстрированный в [29] способ получения «решётки» кольцевых закрученных микропучков методом дифракции Бесселева пучка на двумерной решётке круглых отверстий позволяет «запустить» одновременно группу закрученных плазмонов на системе параллельных проволочек.

Работа выполнена при поддержке гранта РНФ 1912-00103. При выборе расчетных параметров использованы результаты экспериментов, выполненных в ИЯФ СО РАН с использованием оборудования ЦКП «СЦСТИ» на базе УНУ «Новосибирский ЛСЭ».