Оптимизация параметров каскадного кода по критерию максимума граничного значения полосы частот помехи и выбор алгоритма декодирования

Для канала передачи данных с ППРЧ помеха в части рабочей полосы частот, занимаемой спектром сигналов, имеет импульсный характер. Для практики характерен случай, когда совместно с импульсной (узкополосной) помехой действует непрерывная (широкополосная) помеха [1–3]. Кроме того, доказано [4], что при ППРЧ с большим числом рабочих частот наихудшая помеха в каждый момент времени равномерно выбирает часть из них, на которую воздействует с одним превышением, а на оставшуюся часть - с другим. Такая помеха может быть представлена как смесь двух помех - заградительной и сосредоточенной в части полосы ППРЧ, определяемая р = А ^ _помехи / A F _ППРЧ.

Известно, что для систем связи (СС) с ППРЧ и помехоустойчивым кодированием существует значение ρ гр [5, 6] части полосы, накрытой помехой, характеризующееся тем, что при ρ ≤ ρ гр независимо от мощности помехи обеспечивается заданная достоверность передачи информации.

В современных помехоустойчивых СС с ППРЧ полоса частот может составлять 250 МГц и более [7, 8]. Для таких СС характерно воздействие помехи в части полосы ППРЧ, одним из определяющих параметров которой является ргр.

Расчет граничного значения части полосы ППРЧ, накрытой помехой, при жестком декодировании

В каналах передачи данных с ППРЧ часто используется каскадное кодирование, на внутренней ступени которого применяется ансамбль из М ортогональных сигналов (ортогональный код ( n ₂=М, k ₂=log₂M)), а на внешней - код Рида-Соломона (РС) ( n i , k 1 ).

При жестком декодировании вероятность ошибки в блоке РС кода определяется выражением [9]

СгЕ^ЛИ1-^#'" •                ® z=/+l где t - количество исправляемых ошибок в блоке; n 1 - общее число недвоичных символов (импульсов) в блоке РС кода; С', - число сочетаний из n 1 по i; Pe(р) - вероятность ошибочного приема символа (вероятность ошибочного различения ортогональных сигналов).

В свою очередь, вероятность ошибочного различения ортогональных сигналов при когерентном приеме в канале с ППРЧ и действием двух помех определяется соотношением [9]

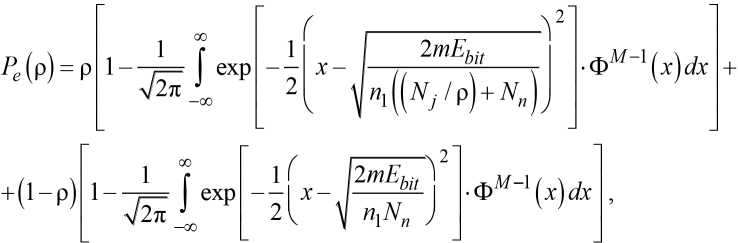
где М - объем ансамбля ортогональных сигналов, используемых для передачи каждого символа кодового слова; m - количество информации, переносимое блоком кода (бит); Nj – спектральная плотность мощности помехи (шума), сосредоточенной в части полосы ППРЧ; Nn – спектральная плотность мощности помехи (шума) во всей полосе ППРЧ; Ebit – энергия х t2

1 Г — сигнала, приходящаяся на один бит переданной информации;

– интеграл

вероятности.

В формуле (2) первое слагаемое определяет зависимость P e от N j и N n (сигнал излучен на частотной позиции, на которой действуют две помехи), а второе - только от N n (сигнал излучен на частотной позиции, на которой лишь помеха во всей полосе). Для расчета р_гр спектральная плотность мощности помехи, накрывающая часть полосы, N j → ∞. Тогда первое слагаемое в формуле (2) равно ρ. В результате уравнение (2) принимает вид

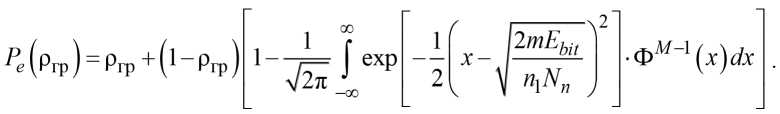
Для нахождения значений ρ_гр уравнение (3) было решено численно в MatLab с помощью функции fzero. В результате расчетов для РС (31, к 1 ) при вероятности ошибки P e (р_гр), соответствующей вероятности ошибки в одном бите P_bit < 1,5 • 10^-4, получена зависимость р_гр от отношения сигнал/шум E_bit / N n для различных РС кодов при М = 32 (рис. 1).

Анализ графиков (рис. 1) показывает, что при условии E_bit / N n = 15 дБ р_гр для кода РС (31, 1) становится меньше, чем для кода РС (31, 3). Таким образом, ρ гр принимает максимальное значение для кода РС (31, 3), а при E_bit / N n = 10 дБ р_гр принимает максимальное значение для кода РС (31, 7). При заданном n 1 и отношении E_bit / N n существует оптимальная скорость РС кода r = к 1 / n 1 , при которой р_гр принимает максимальное значение р_гр max.

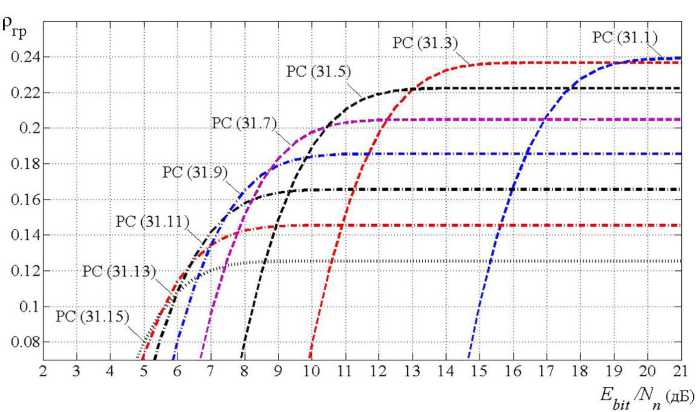
Рис. 1. Зависимость ρ гр от отношения сигнал/шум E bit / N n

Fig. 1. Dependence of ρ гр on the signal-to-noise ratio E bit / N n

Оптимизация параметров каскадного кода по критерию максимума граничного значения полосы частот помехи при мягком декодировании

Для исследования зависимости ρ гр max от E bit / N n и параметров каскадного кода в каналах с мягким декодированием и одновременным действием на канал двух помех расчетных соотношений нет, поэтому было произведено статистическое имитационное компьютерное моделирование.

Для реализации моделирования разработана математическая модель процесса когерентного приема-декодирования, в том числе мягкого, каскадного кода, и реализующая ее компьютерная программа в среде MatLab [10].

Непротиворечивость результатов моделирования была подтверждена тем, что полученные значения Ргр для алгоритма жесткого декодирования отличаются не более чем на 5 % от расчетных значений ρ гр , полученных в результате численного решения уравнения (1).

В соответствии с определением ρ_гр для получения значений Ргр при моделировании было задано отношение сигнал/помеха E bit / N n = –20 дБ (при моделировании E bit = const ).

Кроме помехи в части полосы ППРЧ в модели предусмотрено действие помехи (шума) во всей полосе частот СС, характеризующееся отношением сигнал/шум E bit / N n = 15; 10; 5 дБ. Моделирование производилось при заданной достоверности передачи информации, определяемой вероятностью ошибки на один бит передаваемой информации P bit ≤ 1,5 ∙ 10^–4.

Результаты моделирования когерентного приема – мягкого декодирования по минимуму обобщенного расстояния (МОР) [11] для каскадных кодов (сигнально-кодовых конструкций – СКК) на основе кодов РС (15, k 1 ), РС (31, k 1 ), РС (63, k 1 ), РС (127, k 1 ) приведены соответственно на рис. 2–4.

По результатам анализа полученных графиков можно сделать следующие выводы:

• 1.    Для каналов с исследованными СКК на интервале 0,68 <  r < 1, при n ₁ – const , изменение E bit / N n практически не влияет на значение Рп>.

• 2.    Для различных отношений E bit / N n и заданном n 1 существует максимальное значение Ргр max, которому соответствует оптимальная скорость РС кода r : при E_bit / N_n = 15 дБ – r ≈ 0,03; E bit / N n = 10 дБ – r ≈ 0,1; E bit / N n = 5 дБ – 0,3 <  r < 0,4.

• 3.    С уменьшением E bit / N n скорость РС кода r , при котором Ргр max, увеличивается.

• 4.    При неизменном значении E_bit / N_n = const максимальное значение Ргр max растет с увеличением n 1 .

• 5.    Для каждого значения отношения сигнал/помеха E bit / N n можно оптимизировать параметры РС кода таким образом, чтобы значения Ргр были максимальными.

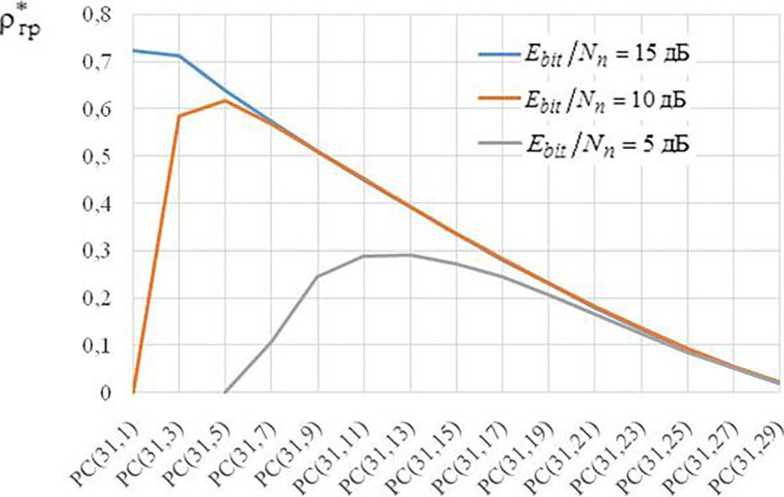
Рис. 2. Зависимость Ргр от характеристик СКК при k ₂ = 5

Fig. 2. Dependence of Ргр on the characteristics of the SCC at k ₂ = 5

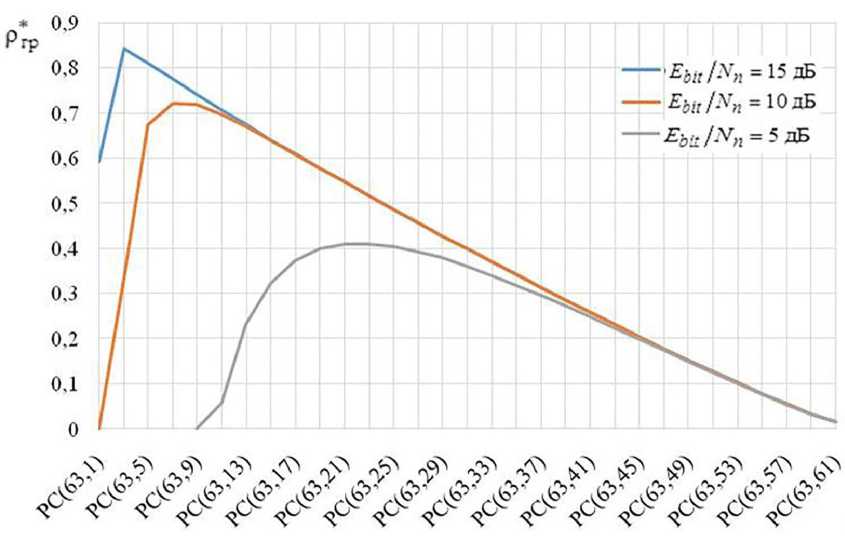
Рис. 3. Зависимость Ргр от характеристик СКК при k 2 = 6

Fig. 3. Dependence of Ргр on the characteristics of the SCC at k 2 = 6

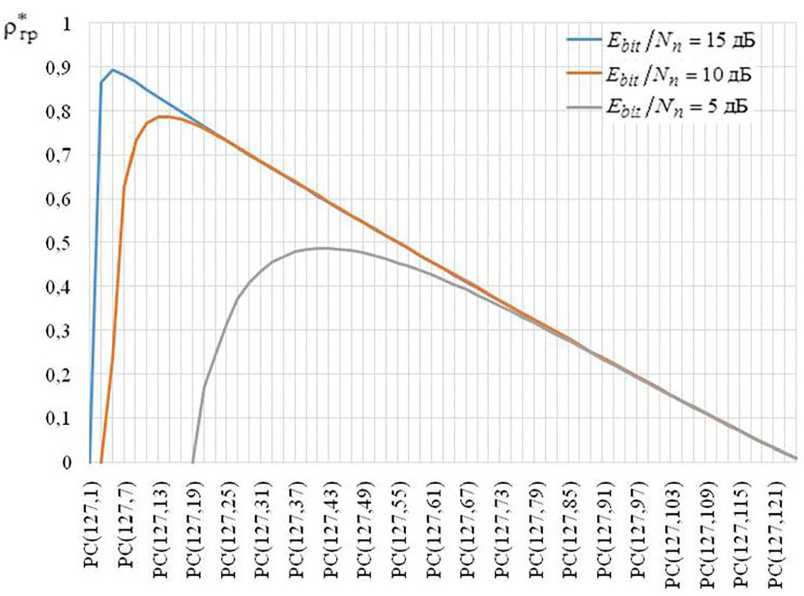
Рис. 4. Зависимость Ргр от характеристик СКК при k 2 = 7

Fig. 4. Dependence of Ргр on the characteristics of the SCC at k 2 = 7

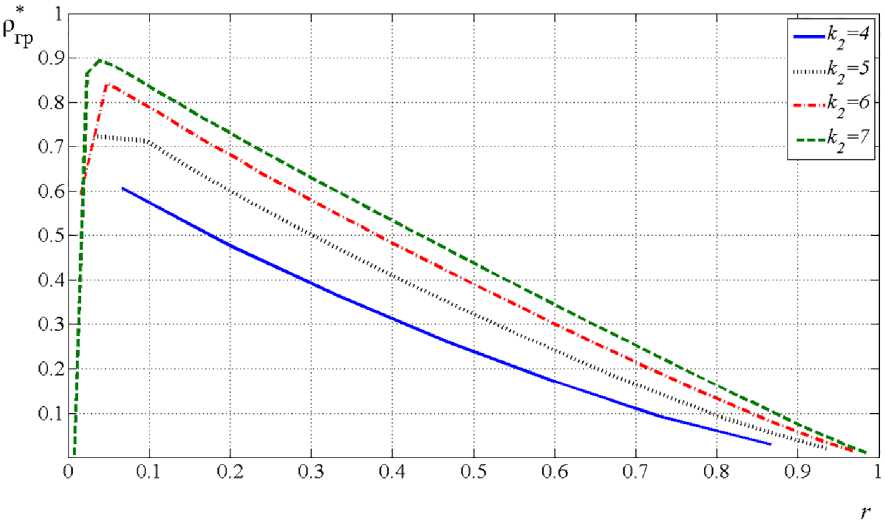
Рис. 5. Зависимость Ргр от скорости кода r

Fig. 5. Dependence of Ргр on the code rate r

Представляет интерес получение Ргр для бóльших значений n ₁ = 2 ^{k 2} – 1.

На рис. 5 представлены графики зависимости Ргр от r для E bit / N n = 15 дБ. При фиксированном значении r можно предположить зависимость Ргр от k 2 . Программа MatLab позволяет аппроксимировать полученные данные. Наиболее точные результаты дает алгоритм аппроксимации Rational Trust-Region (MATLAB R2013b 8.2.0.701), определяемый выражением

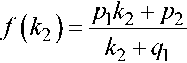
где p ₁, p ₂, q ₁ – коэффициенты аппроксимации. При r = 0,2 коэффициенты принимают значения p 1 =1,01; p 2 =2,471; q 1 =0,7228. Увеличение количества отсчетов, участвующих в аппроксимации, повышает точность экстраполяции (табл. 1).

Таблица 1. Отклонение экстраполированных значений Ргр от полученных в результате моделирования

Table 1. Deviation of extrapolated Ргр values from those obtained as a result of modeling

Участвуют в аппроксимации	Экстраполированные (%)
	k 2 =8	k 2 =9	k 2 =10
k 2 = 4…7	0,6	1,82	1,75
k 2 = 4…8	-	1,29	1,03
k 2 = 4…9	-	-	0,022

Выбор алгоритма декодирования

В результате моделирования были получены и значения Ргр при различных алгоритмах декодирования, в том числе и мягких. В качестве мягких алгоритмов использовались: алгоритм со стиранием наименее надежных l = n – k – 2 t символов и исправлении до t ошибок в оставшихся [12]; алгоритм Бородина [13], основанный на стирании наименее надежных l = n – k символов ( t = 0); алгоритм МОР ( t = 0)… ( n – k ), усеченный МОР – алгоритм [14], в котором реализуются первые три попытки алгоритма МОР ( t = 0…2).

При моделировании алгоритмов мягкого декодирования расчет апостериорной вероятности, определяющей наиболее надежные символы, производился с использованием известной (заданной) суммарной спектральной плотности мощности помехи (шума). Результаты моделирования для СКК на основе РС (31, k ) и E_bit / N_n = 15; 10; 5 дБ представлены на рис. 6–8.

Полученные графики показывают, что величина Ргр max принимает наибольшее значение при E bit / N n = 15 дБ и декодировании по алгоритмам: Бородина, МОР и усеченный МОР. С уменьшением E_bit / N_n до 5 дБ эффективность алгоритма Бородина по Ргр уменьшается. При декодировании по алгоритмам МОР и усеченный МОР величина Ргр max принимает наибольшее значение.

Заключение

• 1.    За счет оптимизации параметров каскадного кода можно обеспечить граничное для помехи значение Ргр части полосы частот канала с ППРЧ, превышающее 0,89. Это означает, что для достижения заданного помехового эффекта противник должен ставить помеху, накрывающую не менее 89 % полосы ППРЧ.

• 2.    За счет выбора алгоритма декодирования можно обеспечить увеличение Ргр в 2,5 раза и более при переходе от алгоритма жесткого декодирования к оптимизированному алгоритму мягкого декодирования.

• 3.    При увеличении интенсивности помехи во всей полосе Ргр max уменьшается.

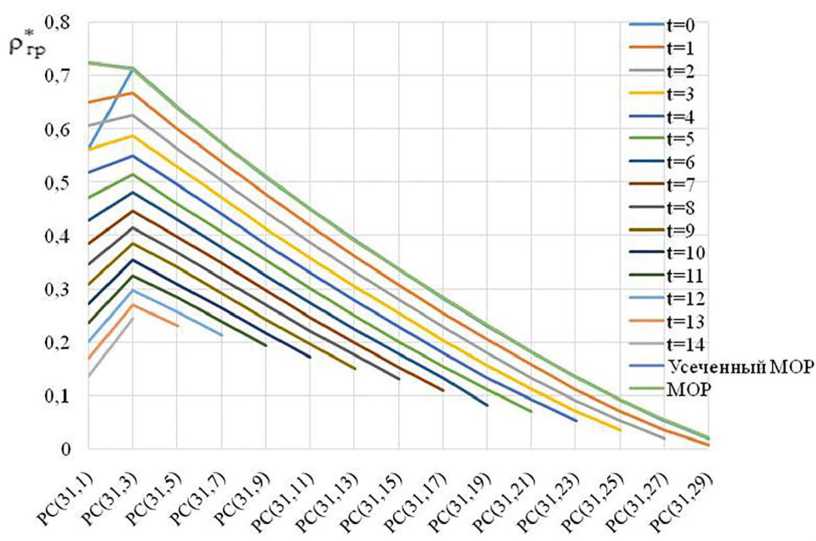
Рис. 6. Зависимость Ргр от характеристик СКК и алгоритма приема-декодирования при E bit / N n = 15 дБ

• Fig. 6.    Dependence of Ргр on the characteristics of the SCC and the receive-decoding algorithm at E bit / N n = 15 дБ

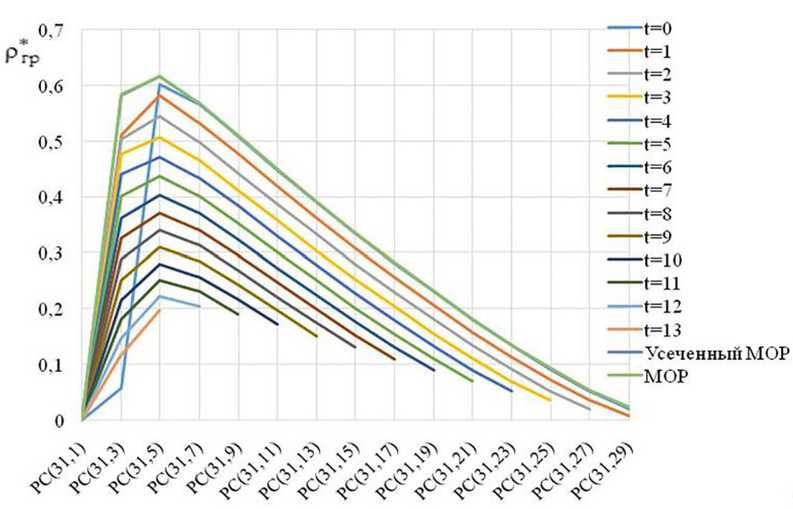
Рис. 7. Зависимость Ргр от характеристик СКК и алгоритма приема-декодирования при E bit / N n = 10 дБ

• Fig. 7.    Dependence of Ргр on the characteristics of the SCC and the receive-decoding algorithm at E bit / N n = 10 дБ

Таким образом, полученные результаты позволяют выбрать параметры СКК, а также алгоритмы декодирования, обеспечивающие максимальные значения ρ гр в заданной помеховой обстановке.

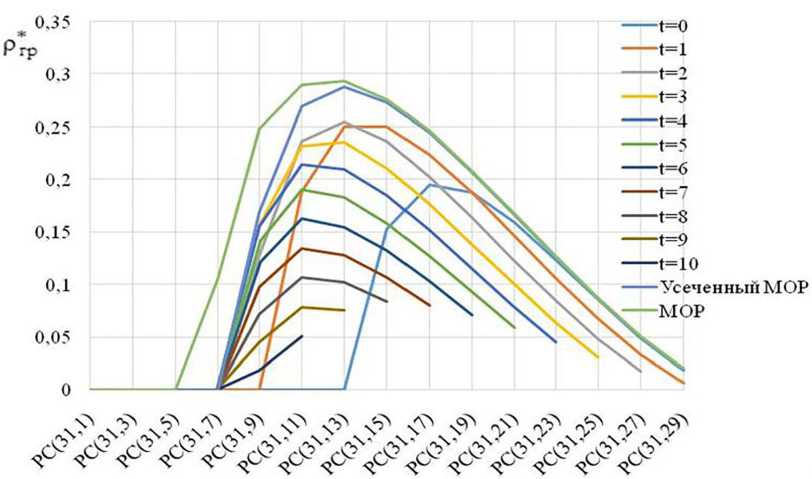
Рис. 8. Зависимость Ргр от характеристик СКК и алгоритма приема-декодирования при E bit / N n = 5 дБ

Fig. 8. Dependence of Ргр on the characteristics of the SCC and the receive-decoding algorithm at E_bit / N_n = 5 дБ