Оптимизация параметров коммутационных узлов, работающих по системе с ограниченной очередью

В настоящей работе выполнена оптимизация параметров коммутационных узлов по экономическим показателям с использованием методов теории массового обслуживания.

Эффективность систем массового обслуживания (СМО) можно характеризовать большим числом различных количественных показателей.

При выборе оптимальных параметров систем массового обслуживания по экономическим показателям можно использовать функцию стоимости потерь в системе [1].

Функция стоимости потерь для системы с ожиданием

G n = ^ож М ож + q nk ( s - M зан ) + q k M зан ) T , (1)

где s – количество каналов; q – стоимость потерь, связанных с простаиванием запросов в очереди в единицы времени; q _nk – стоимость единицы времени простоя канала; q k - стоимость эксплуатации каждого канала в единицу времени; М _ож – среднее число запросов, стоящих в очереди; M_зан – среднее число каналов занятых обслуживанием; T – интервал времени расчета.

Функция стоимости потерь для системы с отказами

G n = (q k M зан + q y W ( s + k) ^ )T,       (2)

где λ - интенсивность входящего потока запросов; k – максимальное число мест ожидания в

очереди; ^q y - стоимость убытков, связанных с уходом из системы запросов; W _{( s +} k) - вероятность того, что все s каналы и k мест ожидания заняты обслуживанием.

Функция стоимости потер для смешанных (комбинированных) СМО

^G n = ^[q nk ^(s ~^М зан) ^{+ q} ож ■ ^М ож ⁺ q y - WW s + k ) "^ ⁺ q k " ^М зан ^]Т " ⁽³⁾

В комбинированных СМО могут найти применение следующие варианты ограничений:

• -    число запросов, стоящих в очереди, ограничено, на время пребывания запросов в очереди и системе ограничения не накладываются;

• -    число запросов, стоящих в очереди, и время пребывания запросов в системе ограничены.

При выборе оптимальных параметров коммутационных узлов, работающих по системе с ограниченной очередью, по экономическим показателям используем функцию стоимости потерь для комбинированной системы (3).

В ⁽³⁾ параметры W ( s + k ) , М ож , M зан для Коммутационного узла,работающего по системе с ограниченной очередью,определяются как функция распределения числа запросов системы массового обслуживания (СМО) в комбинированной системе [2]:

s

( s + k )

ρ

s    jt^      (s+2.>

W« =Z + Z , L j=0 j!     j=(s+1) s!s

⁽ j ^-s)

Wj=⎨

W , ,     0 < j < s ,

-P^- Wo, j > s s!s(j-s) 0

s + k ^{ρ WW} ( s + k )      s k s ! ^WW 0

w

ож

k

= Z jW ( s . k )

j = 1

w

зан

s

=∑jWj j=1

где ρ – интенсивность поступающей нагрузки; W ₀ – вероятность того, что в системе нет ни одного запроса; W j - если j <  s вероятность того, что s каналы заняты обслуживанием; W _j если j >  s вероятность того, что s каналы заняты обслуживанием и j запросов находятся в очереди.

Алгоритм определение минимальных значений функций стоимости потерь G _п для различных значений нагрузок ( ρ ), числа каналов ( s ) и мест ожиданий ( k ) имеет следующий вид.

1. Вводим исходные данные:

вания, реализован с помощью программы Excel 2003, а также составлена программа на алгоритмическом языке Turbo Pascal.

В качестве исходных данных использованы нормативные данные 2008 г. Министерства Связи и Информационных технологий Азербайджанской Республики.

Допустим:

• -    qnk = 0,445 $ в мин.;

• -    qож = 7,42.10-4 $ в мин.;

• -    qу = 0,004 $ в мин.;

• -    стоимость эксплуатации каждого канала в месяц составляет 0,937 ;

• -    q k = з⁰⁹^ = ^2,17 •10 ^{- 5} $ в мин.;

• -    Х = 25 пакетов/С;

• -    средняя длина пакета 144 байт = 144,8 = 1151 бит;

• -    пропускная скорость линии 64000 бит/С;

• -    среднее время обслуживания каждого пакета

  T_s =1152/64000 = 0,018 С;

• 2.    Вычисляем          ^ρ .

-    ρ = λ Ts = 25.

Расчеты выполняются для различных значений нагрузок ( ρ ). На рис. 1. приведены зависимости стоимости потерь для различного числа каналов ( s = 1…4) и определенного количества мест ожиданий ( k = 4).

s,    k, ρн , ρк , Δρ, qnk , qож , qу .

j

j!

ρj

• 3.    Вычисляем Q = Q +--——-.

• 4.    Вычисляем W 0 = ( P + Q ) ^{- 1}.

• 5.    W _j – вычисляется по формуле (5).

• 6.    W ( s + k ) — вычисляется по формуле (6).

• 7.    M _ож – вычисляется по формуле (7).

• 8.    M _зан – вычисляется по формуле (8).

• 9.    G _n вычисляется по формуле (3).

• 10.    Печатаем результаты: G _n ,ρ,s,k .

( j - s )

s ! s ⁽ j )

Алгоритм оптимизации числа каналов коммутационного узла, работающего по комбинированной системе обслуживания, так же, как и для коммутационного узла, работающего по системе с ожиданием, заключается в последовательном расчете значений целевой функции G _n при различных значениях числа каналов связи и количества мест ожиданий.

Данный алгоритм оптимизации стоимостной характеристики коммутационного узла, работающего по комбинированной системе обслужи-

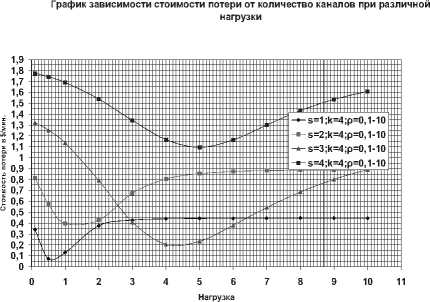
Рис.1. Зависимость стоимости потери от изменений нагрузки при различном количестве каналов ( s =1-4 ) для мест ожиданий k = 4

Из рис. 1. видно, что при многоканальном обслуживании ( s = 1…4) и при количестве мест ожиданий k = 4 минимальные значения стоимости потерь составляют:

• -    при s = 1 и ρ = 0,7; Gmin = 0,0516 $ в мин.;

• -    при s = 2 и ρ = 1,4; Gmin = 0,3488 $ в мин.;

• -    при s = 3 и ρ = 4,3; Gmin = 0,1928 $ в мин.;

• -    при s = 4 и ρ = 5; Gmin = 1,0958 $ в мин.

Из приведенных результатов можно сделать вывод о том, что при проектировании коммутационного узла,работающего по комбинированной системе обслуживания, для оптимизации числа каналов и количество мест ожиданий необходимо учитывать найденные минимальные значения стоимости потерь для оптимальных значений нагрузок и количества мест ожиданий.