Оптимизация параметров конструкции бионического плавающего робота для мониторинга природных и техногенных объектов в гидросфере

Мониторинг состояния гидросферы является частью общей системы наблюдений за окружающей природной средой. В настоящее время во всем мире ведется активная разработка различных роботизированных устройств, способных решать задачи исследования водных объектов, такие как:

• •    разведка недр мирового океана и поиск полезных ископаемых;

• •    мониторинг загрязнения вод и их очистка;

• •    поисковые и спасательные работы;

• •    проверка состояния подводных трубо-и топливопроводов;

• •    океанографические исследования (изучение морских течений, миграции морских животных, учёт их ареала и популяции и т.п.);

• •    обследование и подъем затонувших объектов;

• •    морская археология.

При этом комплексность научных исследований водных объектов требует определения множества физических и химических параметров, таких как температура воды, скорость и направление течения, химический состав воды, а также определения местоположения подводных объектов (подвижных и неподвижных). Обработка данной информации может осуществляться

Яцун Сергей Федорович, доктор технических наук, профессор, заведующий кафедрой теоретической механики и мехатроники

Политов Евгений Николаевич, кандидат технических наук, доцент кафедры теоретической механики и мехатроники

Тарасова Елена Сергеевна, аспирантка на стационарных пунктах мониторинга, но сбор подобной информации – задача именно подвижных подводных аппаратов. В данной статье представлено описание конструкции и методики оптимизации параметров опытного образца робота-рыбы, математическая модель которой предложена в [1]. Опытный образец предназначен для экспериментальной проверки предложенной конструкции робота и средств его управления в условиях натурных испытаний в водной среде.

Описание конструкции бионического плавающего робота. В соответствии с принятой и рассмотренной в [1] трехзвенной кинематической схемой (рис. 1) плавающего робота, основанного на бионических принципах движения, в конструкции робота необходимо предусмотреть следующие основные приводы и подсистемы: привод хвостового плавника; привод предхвостия; подсистему динамического погружения и всплытия с приводом боковых плавников; подсистему вертикального погружения и всплытия; подсистему видеонаблюдения; подсистему освещения; подсистему электропитания; подсистему навигации.

Хвостовой плавник и предхвостие приводятся в движение кривошипно-коромысловыми механизмами, в которых вращение кривошипов обеспечивается сервоприводом фирмы Parallax серии Standard Servo (#900-00005). Данные электроприводы оснащены встроенной системой автоматического управления, обеспечивающей точное позиционирование угла поворота вала в пределах от 0º до 180º или непрерывное вращение с заданной скоростью. В подсистеме динамического погружения и всплытия также используется сервопривод модели Standard Servo (#900-00005) для задания необходимого угла поворота парных боковых плавников в диапазоне от нуля до 180 градусов. Это позволяет изменять направление движения робота в вертикальной плоскости, то есть осуществлять погружение (всплытие) за счет движения хвостового плавника. Такое погружение или всплытие робота будем считать динамическим.

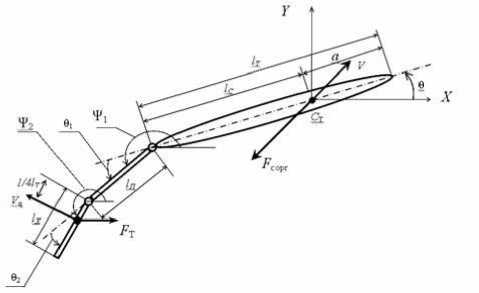
Рис. 1. Расчетная схема бионического плавающего робота в горизонтальной плоскости: X-Y – прямоугольная абсолютная система координат; l _T – длина «тела» робота; l _П – длина хвостового стебля; l _Х – длина хвостового плавника; V – вектор абсолютной скорости центра масс С Т ; V q – вектор линейной скорости точки хвостового плавника, отстоящей на расстоянии ¼ его длины от оси вращения; θ – угловая координата центральной продольной осевой линии тела робота; θ 1 и θ 2 –относительные углы поворота хвостового стебля и хвостового плавника соответственно вокруг своих осей вращения; ψ 1 и ψ 2 – абсолютные угловые координаты положения хвостового стебля и хвостового плавника соответственно.

Кроме того, предусмотрена система вертикального погружения (всплытия), необходимость которой продиктована возможной потребностью мониторинга вертикальных объектов в гидросфере (опорных колонн, свай, подводных бортов кораблей и т.д.), а также возможными ограничениями водного пространства. Подсистема вертикального погружения (всплытия) представляет собой гидроцилиндр с приводом линейного движения для приема или вытеснения забортной воды, что позволит управлять величиной архимедовой силы. Подсистема автономного электропитания включает основную аккумуляторную батарею, рассчитанную на бесперебойную работу всех приводов в штатном режиме (не менее 30 мин.), а также аварийную аккумуляторную батарею, необходимую для аварийного всплытия робота-рыбы.

Первые испытания изготовленного опытного образца робота-рыбы (рис. 2) с дистанционным управлением показали, что он может перемещаться в водной среде на расстояние до 150 м. Данное устройство позволяет исследовать влияние параметров конструкции (площади и длины хвоста, частоты и амплитуды колебаний хвоста) на динамические характеристики мобильного робота (скорость плавания, маневренность и т.д.), а также обеспечит возможность других экспериментальных натурных исследований.

Рис. 2. Фото испытания опытного образца бионического плавающего робота

Оптимизация параметров бионического плавающего робота. В качестве основных параметров, определяющих эффективность движения робота в горизонтальной плоскости, будем рассматривать следующие: ω 2 – частота угловых колебаний хвостового плавника; θ 2 – амплитуда угловых колебаний хвостового плавника; S – площадь боковой поверхности хвостового плавника; l х – условная длина хвостового плавника; M – масса тела робота-рыбы. Оценку функциональных возможностей движения плавающего бионического робота будем производить по следующим характеристикам:

• -    V – скорость плавания – скорость прямолинейного движения робота вдоль его основной оси симметрии. Определяет эффективность транспортировки средств мониторинга окружающего подводного пространства в горизонтальной плоскости;

• -    Y – боковое смещение центра масс робота. Определяет непостоянство направления средств мониторинга окружающего пространства;

• -    θ – угловое «виляние» тела робота относительно вертикальной оси, проходящей через его центр тяжести. Определяет нестабильность направления оптической оси аппаратуры

видеонаблюдения и углового обзора исследуемого подводного пространства;

• -    μ= R /( lх + l П + l t ) – коэффициент маневренности в горизонтальной плоскости, где R – радиус кривизны траектории поворота робота на 180 градусов, ( lх + l П + l t ) - общая длина робота. Определяет пространство для разворота робота в горизонтальной плоскости.

Для решения задач оптимизации используется стандартный план Рехтшафнера [2], на основании которого была составлена универсальная программа расчёта в среде MathCAD «Оптимальное планирование эксперимента» [3]. В качестве критериев оптимизации рассматриваемого устройства примем скорость плавания V и угол θ «виляния» корпуса робота относительно вертикальной оси, проходящей через центр тяжести робота. Причем первый из них необходимо получать наибольшим, а второй – наименьшим из возможных значений с учетом определенных ограничений, накладываемых на управляемые параметры системы. Тогда комплексный критерий оптимизации (целевая функция) может быть представлена в следующем виде:

K = k 1 V + k 2 /θ →max, (1)

где k 1 и k 2 – «весовые» коэффициенты, корректирующие вклад каждого из критериев качества в комплексный критерий оптимизации. С учетом диапазонов изменения критериев V и θ примем значения k 1 =10; k 2 =400 так, чтобы вклад каждого из составляющих критерия был одного порядка.

В результате предварительного исследования движения плавающего робота в горизонтальной плоскости установлены наиболее значимые параметры его модели, существенно влияющие на кинематические характеристики и функциональные возможности. Для оптимизации параметров конструкции разрабатываемого робота по принятой целевой функции (1) в качестве варьируемых факторов были приняты: X 1 – частота колебаний хвостового плавника ω ; X 2 – амплитуда угловых колебаний хвостового плавника θ 2 ; X 3 – площадь боковой поверхности хвостового плавника S ; X 4 – длина хвостового плавника lx . Интервалы изменения варьируемых факторов и значения их трёх уровней представлены в таблице 1.

Таблица 1 . Интервалы и уровни изменения варьируемых факторов

Факторы	Уровни			Интервал варьирования	Размерность
	-1	0	+1
X 1	2	4	6	2...6	рад/c
X 2	10	20	30	10...30	градусы
X 3	0,01	0,02	0,03	0,01...0,03	м2
X 4	0,10	0,15	0,20	0,1...0,2	м

Остальные параметры модели робота были приняты постоянными: M=2 кг; l п=0.1 м, lt =0.3 м ; J =0.04 кг м². Расчёт коэффициентов аппроксимации функции отклика полным полиномом второго порядка (регрессионный анализ) дал следующие результаты:

K( X )=9,0 + 8,93 X 1 – 2,0 X 2 – 2,62 X 3 + 8,64 X 4 + + 6,61 X 1 ² – 1,31 X 2 ²+3,54 X 3 ² – 5,11 X 4 ²–

– 4,83 X 1 X 2 ++ 4,13 X 1 X 3 +5,08 X 1 X 4 + 1,87 X 2 X 3 –

–7,26 X 2 X 4 + 4,39 X 3 X 4              (2)

Поиск максимума функции (2) в пятимерном пространстве выполнен методом половинного деления шага по каждой переменной и позволил определить значение вектора варьируемых факторов в нормированном виде X =( X 1, X 2, X 3, X 4), соответствующее точке максимума: X опт= (1, -1, 1, 1). В размерном виде этой точке соответствуют значения:

• X 1 =1 – частота колебаний хвостового плавника ω опт =6 рад/с;

X 2= –1 – амплитуда угловых колебаний хвостового плавника θ 2опт = 10⁰;

X 3 =1 – площадь боковой поверхности хвостового плавника S опт =0,03 м²;

X 4 =1 – длина хвостового плавника lt опт =0,2 м.

Определенным таким образом оптимальным значениям параметров модели робота соответствуют следующие кинематические характеристики его движения в горизонтальной плоскости: Vопт=0,214 м/с; θопт = 4,00. Анализ полученных результатов свидетельствует о том, что при найденном оптимальном соотношении параметров модели робота можно достичь достаточно высокой скорости плавания (Vопт=0,214 м/с) бионического робота-рыбы при малом (θопт = 4,00) «вилянии» его корпуса относительно вертикальной оси, что является важным при проведении видеомониторинга окружающего водного пространства, а также природных и техногенных объектов, находящихся в нем.

Выводы: в работе рассмотрены и приняты к использованию принципы оптимального планирования экспериментальных исследований, с их учетом были составлены методика и программа натурных испытаний разрабатываемого опытного образца бионического плавающего робота. Для целей оптимизации параметров конструкции робота и управляющих сигналов были выбраны варьируемые факторы, наиболее значимые и существенно влияющие на функциональные возможности и характеристики движения. В результате предварительных исследований был сформирован комплексный критерий оптимизации для целевой функции, учитывающий скоростные качества движения робота и стабильность положения тела робота, что является важным при проведении видеомониторинга окружающего водного пространства, а также природных и техногенных объектов, находящихся в нем.

Работа выполнена в рамках реализации Федеральной целевой программы «Научные и научнопедагогические кадры инновационной России» на 2009-2013 годы по проблеме «Разработка бионического плавающего робота для мониторинга природных и техногенных объектов в гидросфере» (гос. контракт № П971) .