Оптимизация параметров линейного сглаживания хроматографических пиков

Каждое измерение — это сумма исходного сигнала, случайных шумов и систематических погрешностей измерения. Шумы возникают в электронных системах регистрации при изменении условий окружающей среды и т.д. Основная задача при сглаживании цифрового сигнала — максимально точная оценка исходного сигнала или его параметров на основании массива измеренных данных. В этой работе изучается влияние линейных методов сглаживания на базовые метрологические параметры пика — его площадь и высоту. Эти параметры используются для оценки количества вещества, и минимизация их погрешности способна уменьшить погрешность оценки.

ТЕОРИЯ

О линейном сглаживании

Все методы, основанные на скользящем взвешенном среднем, называются линейными методами сглаживания. Это название происходит от математического термина "линейное преобразование" (в одномерном случае означающего примерно то же, что и "взвешенное среднее"), а не от аппроксимации функции прямолинейной зависимостью. Более строго — линейным является метод, для которого результат операции сглаживания S ( a + n ) суммы сигнала a и шума n совпадает с суммой результатов сглаживания сигнала и шума по отдельности S ( a + n ) = S ( a ) + S ( n ), а также для любого действительного k выполняется равенство S ( k ∙ a ) = k ∙ S ( a ).

Не соответствующие этим условиям методы называются нелинейными, и в данной работе их поведение исследоваться не будет.

Свертка функций и скользящее среднее

Скользящее взвешенное среднее имеет непосредственное отношение к операции над математическими функциями, называемой сверткой. Именно, сверткой двух функций f(x) и g(x) называ- со ется функция (f * g)(x)= J f (y)g(x - y)dy.

-о

Дискретный аналог свертки — скользящее взвешенное среднее, в котором интегрирование n превращается в суммирование Yk = ^ wyk -,, i=-n где прописной буквой Yk обозначено сглаженное значение в точке с индексом k, wi — вес точки с индексом (k – i), yk – i — несглаженное ("сырое") значение сигнала. Размер окна сглаживания Nf в таких обозначениях равен Nf = 2n + 1.

Математические моменты пиков и их изменения при сглаживании

Математические моменты пика определяются выражениями:

со

M 0 = J P ( x )d x ,

-о

1 Г

M 1 =--- [ xP ( x )d x ,

M 0 -о

to

Mi = M ^x - M1)‘P(x)dx, (3) -to где P(x) — функция от аргумента x, описывающая пик, i — порядок момента. Моменты порядка два и более называются центральными, поскольку начало координат оси x для этих моментов сдвинуто в центр масс распределения, равный M1.

M 0 — площадь. Нулевой момент свертки равен произведению нулевых моментов функций

M 0( f _* g ) = M 0( f ) ∙ M 0( g ).

Для того чтобы не изменилась площадь сглаживаемого пика, на веса налагаются ограничения. Именно, площадь не изменяется, если сумма весов взвешенного среднего равна единице.

M 1 — время удерживания (центр масс) свертки равен сумме первых моментов функций

M 1( f * g ) = M 1( f ) + M 1( g ) .

Для того чтобы первый момент не изменялся, нужно, чтобы сглаживание производилось таким окном, первый момент которого равен нулю. Проще всего это достигается симметричной формой щели: w_–i = w_i . Для того чтобы сглаживание не приводило к изменению сетки оцифровки, обычно используют окна с нечетным числом точек, как приведено в наших обозначениях. Симметричное окно с четным числом точек будет соответствовать сдвигу сетки оцифровки на половину отсчета.

В хроматографии удерживание обычно измеряется по положению вершины пика. Еще два метода оценки удерживания — положение "центра масс" M 1 и время выхода половины площади — обычно не используются.

M 2 — второй центральный момент. Величина σ = M 2 ^1/2 называется стандартным отклонением. Второй момент свертки равен сумме вторых моментов функций:

M 2( f * g ) = M 2( f ) + M 2( g ).

Другое название второго центрального момента — дисперсия. Тем не менее мы в данной работе для простоты понимания текста будем стараться называть дисперсией величины, относящиеся к оси ординат (шумы), а величины, относящиеся к протяженности пика по оси абсцисс, будем называть вторым моментом, подразумевая, что он центральный.

Свертка сглаживающей функции с неотрицательными коэффициентами с пиком приводит к увеличению второго момента сглаженного пика, причем он равен сумме вторых моментов исходного пика и сглаживающей функции. Доказательство этого факта можно найти в теории вероятностей:

неотрицательные пик и сглаживающую функцию можно рассматривать как плотность распределения двух независимых случайных величин, а для них вторые моменты (дисперсии) складываются.

Экспоненциально модифицированная гауссиана (ЭМГ)

Является результатом свертки гауссианы и экспоненты. Форма пика, хорошо описывающая хроматографические пики, может возникать как из-за применения для фильтрации шумов RC-цепочки или экспоненциального цифрового фильтра, так и по причинам, не имеющим отношения к электронике или сглаживанию. Такая форма, к примеру, получится, если после идеальной хроматографической колонки, дающей гауссову форму пика, поставить камеру смешения, моделирующую не-идеальность колонки. Обычно в литературе формула ЭМГ [1–3] записывается как f^ -1 ° 2 1

F (t ) =     I • e ^{V T} 2 erfc ^f( ^ -T ⁺ 7 )) , (4)

т 2               ^ V2 V °   т))

где t — время, h — высота гауссианы, σ — сигма гауссианы, μ — позиция гауссианы, τ — время релаксации (параметр экспоненты, используемый для модификации гауссианы),

2z erfc (z) = 1 - erf (z), erf (z) =     [ e"t dt.

π ₀

Момент ЭМГ нулевого порядка равен площади исходной гауссианы, M 1 = μ + τ , M 2 = σ ² + τ ² .

Методы сглаживания

Наиболее популярные варианты фильтров, основанных на скользящем взвешенном среднем, — скользящее среднее арифметическое, метод Са-вицкого—Голея, сглаживание гауссианой [4]. Пример распределения весов для этих методов приведен на рис. 1. Немного подробнее о каждом из методов.

Скользящее среднее арифметическое

Это — один из самых быстрых методов сглаживания. Число операций пропорционально числу точек сглаживаемого массива данных. Сглаженное значение — сумма, деленная на число точек.

Метод Савицкого—Голея

Савицкий и Голей (Голай) [4] предложили способ фильтрации шумов, основанный на методе наименьших квадратов (МНК), который, несмотря на сложность модели, имеет очень низкую вычислительную сложность. Согласно этому методу, 2 n + 1 последовательных равноотстоящих точек

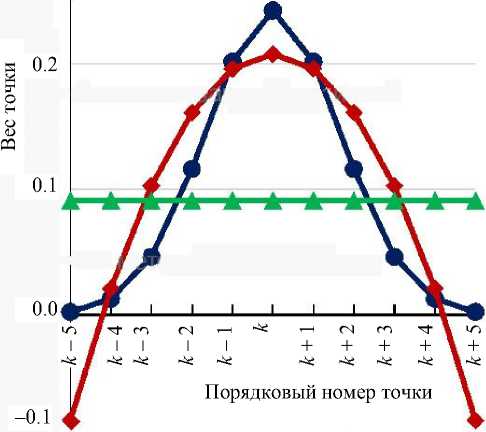
Скользящее среднее

Метод Савицкого—Галея

Сглаживание гауссианой

Рис. 1. Веса точек скользящего взвешенного среднего для нескольких популярных вариантов сглаживания аппроксимируются МНК полиномом 2k-й степени (k < n), и в качестве сглаженного значения используется значение полинома в (n + 1)-й точке. Оказалось, что математически это значение вычисляется путем скользящего взвешенного среднего с весами точек, положительными в центре окна фильтрации и отрицательными на периферии (рис. 1). Результаты фильтрации по Савицкому—Голею совпадают для полиномов степени 2k и 2k + 1. К примеру, скользящее среднее и аппроксимация прямой (соответствующие аппроксимации Савицкого—Голея 0-й и 1-й степеней) в качестве ответа дадут среднее значение сигнала: прямая всегда проходит через центр масс, равный среднему арифметическому, который и выдается в качестве сглаженного значения аппроксимации прямой.

Экспоненциально взвешенное скользящее среднее

Также чрезвычайно быстрый метод сглаживания. Отфильтрованное значение складывается из взвешенной суммы последнего измеренного значения и предыдущего сглаженного:

Y i = α∙y i + (1 – α ) ∙Y i- 1 .

При независящем от времени постоянном коэффициенте 0 <  α < 1 этот метод носит также название экспоненциального сглаживания. Применяющие этот метод обычно не осознают, что из-за того что первый момент сглаживающей функции не равен нулю, экспоненциально взвешенное среднее дает оценку для некоторого индекса (момента) j в прошлом: j = i + 1 – 1/ α , а также то, что такое сглаживание приводит к возрастанию асимметрии сглаживаемого сигнала, в частности гауссиана превращается в ЭМГ.

Многократное сглаживание и сглаживание гауссианой

В случае многократного сглаживания скользящим взвешенным средним отметим интересный эффект, следующий из центральной предельной теоремы теории вероятностей [5]. Если веса скользящего взвешенного среднего неотрицательны и их распределение имеет второй момент, равный M 2, то вне зависимости от метода сглаживания по мере роста числа N повторений результат будет приближаться к однократному сглаживанию скользящим взвешенным средним с весами, распределенными по закону Гаусса, и вторым моментом N∙M 2.

В любом случае, сочетание нескольких проходов взвешенным средним с разным распределением весов будет эквивалентно одному проходу с весами, которые легко вычисляются по весам использованных фильтров. Достаточно сначала выполнить свертку по фильтрам, получив комбинированный, которым затем и выполнять сглаживание функции. Сочетание разных способов сглаживания может иметь смысл, если принципы их работы различны: например сочетание медианного сглаживания и взвешенного среднего при наличии выбросов в исходных данных.

Безусловно, на практике веса гауссианы ограничиваются по величине для того, чтобы сократить размер окна. К примеру, в программе "МультиХром" [6] используются такие параметры гауссианы, что вклад каждой из граничных точек окна составляет 10% от вклада центральной точки и точка находится на расстоянии 2.15 σ от положения вершины.

Медианное сглаживание

В этом методе рассчитывают медианное среднее по 2n + 1 точкам, и оно считается сглаженным значением в центральной (n + 1) точке. Напомним, что медианное среднее находится в середине ок-на/интервала на (n+1)-й позиции (начиная с 1-й) в отсортированном массиве данных. Порядок — по возрастанию или убыванию — роли не играет, поскольку средний элемент в обоих случаях будет один и тот же. Этот метод очень эффективно уби- рает выбросы в данных (или, что то же самое, чрезвычайно устойчив), но меняет (уменьшает) площадь и высоту пика и не является линейным.

Фильтр Калмана

Это on-line фильтр [7], т.е. он ориентирован на фильтрацию значения в последней (по времени) из измеренных точек и использует при формировании нового значения предыдущий результат фильтрации (последнее свойство называется ре-курсивностью). В простейшей реализации — это экспоненциально взвешенное среднее. В общем случае фильтр строит некую самонастраивающуюся модель смены состояний системы и на ее основании производит сглаживание. Фильтр Кал-мана несимметричный, т.е. использует только точки, измеренные ранее анализируемой, игнорируя более поздние. Этот факт можно рассматривать как достоинство (оперативное on-line сглаживание), а можно и как недостаток (используется только половина информации, доступной для оценки сглаженного значения). Фильтр может быть линейным или чаще нелинейным. Свойства фильтра в силу его сложности могут быть переменными на разных участках массива данных.

Коэффициент подавления случайной составляющей погрешности

Коэффициент подавления случайной составляющей погрешности для взвешенного среднего легко вычисляется [8], если учесть тот факт, что сглаженное значение является линейной комбинацией соседних значений, а величина погрешности в суммируемых точках случайна и имеет одинаковую дисперсию. Шумоподавление в точке, вычисленной как взвешенное среднее, равно

K f = σ N ² / D[ Y i ] = 1 / ∑w i ² , (5) где D[ Y i ] — дисперсия сглаженного значения Y i . Обратим внимание, что этот коэффициент шумоподавления относится к подавлению мощности шума. Амплитуда шума при этом уменьшается в √ K f раз.

Нам потребуется зависимость коэффициента подавления погрешности от размера окна сглаживания N f . Проще всего посчитать эту зависимость для скользящего среднего с одинаковыми весами:

D[ Y i ] = σ N ² / N f и K f = N f .

Величина второго момента фильтра приблизительно пропорциональна квадрату размера окна, а стандартное отклонение — размеру. К примеру, второй центральный момент прямоугольной щели скользящего среднего равен M 2[ f ] = ( N f ² – 1) / 12.

В случае фильтра Савицкого—Голея [4] часть весов отрицательна (рис. 1), причем второй момент сглаживающего фильтра для полиномов 2-й и 3-й степеней в точности равен нулю [8]. Второй момент сглаженного фильтром Савицкого—Голея пика не увеличивается, однако платой за это является появление других систематических искажений его формы, которые мы увидим ниже. Выводы настоящей работы к фильтру Савицкого—Голея и любым другим фильтрам, у которых имеются отрицательные коэффициенты, не относятся.

Как и ожидалось, дисперсия случайной составляющей погрешности скользящего среднего уменьшается в N раз, а стандартное отклонение — в √ N раз. Такая же зависимость с точностью до коэффициента характерна для других вариантов распределения весов: сглаживание гауссианой, метод Савицкого—Голея. Указанную закономерность при больших N можно описать формулой как K f ≈ k∙M 2 f ^1/2 , где k — коэффициент пропорциональности, а M 2 f — второй момент фильтра.

Оптимальные параметры сглаживания

Прежде чем что-то оптимизировать, нужно понять, что именно и по каким критериям. Часто используемых параметров пика немного, и их можно разделить на две группы: базовые, используемые для идентификации и расчета количества вещества, и валидационные. Базовых параметров три: удерживание, площадь и высота. Из двух параметров — площадь и высота — обычно используется один. Важных валидационных тоже три: ширина, асимметрия и разрешение между пиками. Мы сознательно не приводим формул расчета валидаци-онных параметров, поскольку их обсуждение не входит в нашу задачу. Если не оговорено особо, пользуемся формулами фармакопеи РФ [9].

Обратим внимание на минимально допустимый темп сбора данных, гарантирующий незначимость погрешностей, связанных с темпом оцифровки. Индивидуальные данные по параметрам приведены в таблице.

Замечания по данным, представленным в таблице

• •    Ширина пика по основанию вычисляется как расстояние по оси абсцисс между точками пересечения базовой линии касательными, проведенными в точках перегиба на переднем и заднем склонах пика. Для пика гауссовой формы эта величина равна 4 σ .

• •    Цифры в таблице относятся к пикам ЭМГ с отношением τ / σ = 3 (фактор асимметрии 2.7), т.е. к "худшему приемлемому по форме" хроматографическому пику.

Минимальная ширина пика по основанию в точках, обеспечивающая приемлемую погрешность вычисления в зависимости от способа оценки параметра

Параметр	По моментам	По аппроксимации
Удерживание	3	7
Площадь	5	9
Высота	—	14
Ширина	5	14
Асимметрия	5	14

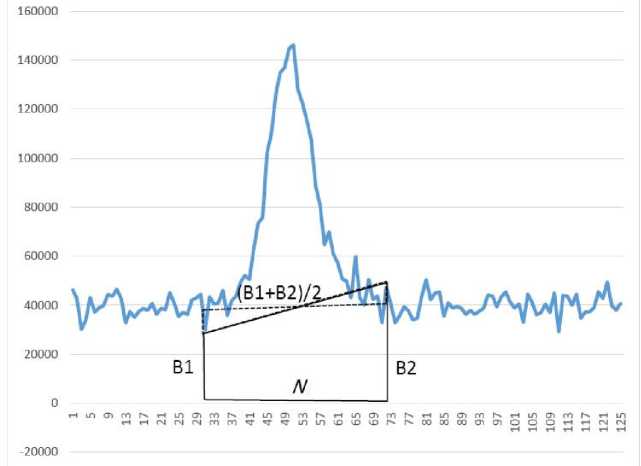
Рис. 2. Базовая линия проведена по фиксированным граничным точкам пика. Сплошной линией обозначена область трапеции под базовой линией. Пунктир обозначает область эквивалентного по площади прямоугольника. B1 — ордината точки начала пика, B2 — конца пика. N — число точек, приходящихся на пик

• •    Оценки выполнены для пиков без шума.

• •    Аппроксимация предполагается полиномиальной, в этом случае площадь вычисляется по методу Симпсона.

• •    Моменты вычисляются по методу трапеций.

• •    Высота не может быть вычислена по моментам пика.

• •    Величины в столбце "По моментам" вычислены по данным работы [10], оценки аппроксимации высоты, ширины и асимметрии — согласно рекомендациям из работы [11], и согласуются с нашими собственными оценками погрешностей параметров [12] при их вычислении с помощью полиномиальной аппроксимации окрестностей целевой точки.

• •    Погрешности параметров соответствуют потребностям валидационных методик, к примеру для площади это 0.1 %. Обратим особое внимание

на то, что оценка параметров пика на основании моментов имеет преимущество в случае узких пиков [10].

Оценка погрешности площади наиболее актуальна для малых пиков, вблизи пределов обнаружения и определения — для таких случаев сглаживание может дать максимальный эффект. Поскольку сигнал в этом случае небольшой, то погрешность измерения в области пика можно считать близкой к погрешности измерения сигнала в области базовой линии, т.е. модель погрешности можно считать гомоскедастичной (погрешности всех измерений одинаковы). Пусть погрешности измерения некоррелированы, имеют нормальное распределение с дисперсией σN2. Предположим, что алгоритм поиска пиков находит точки начала и конца пика по "идеальной" хроматограмме без шума. Базовая линия моделируется прямой, со- единяющей точки начала и конца пика. Площадь пика считается по правилу прямоугольников — для пиков такой способ является лучшим [10, 13, 14], поскольку характеризуется аномально низкой погрешностью интегрирования в случае узких пиков. Такая модель (рис. 2) не в полной мере отражает действительность, в реальности алгоритмы проведения базовой линии могут искать минимальную точку в определенной окрестности. Тем не менее для грубых оценок погрешностей интегрирования модель предопределенных границ удобна. Площадь вычисляется как

A = h (∑ Y i ) – h ∑ ( Y 1 +i (( Y i – Y 1 ) / N )) =

= h (∑ Y i ) – hN ( Y N + Y 1 ) / 2 =A N – A b , (6) где h — шаг оцифровки по абсциссе (постоянная времени), Y_i — отклик детектора в точке с индексом i , N — общее число измерений, приходящихся на пик. Считаем, что индекс первой точки пика равен единице. Тем самым площадь вычисляется как разница двух величин: уменьшаемое — сумма ординат точек внутри области пика, а вычитаемое — площадь под базовой линией, которая может быть вычислена как произведение полусуммы ординат точек начала и конца базовой линии. Введем обозначения Y 1 = B1, Y N = B2 и для простоты выражений положим h = 1, тогда

A b = N (B1 + B2) / 2. (7)

Дисперсия погрешности измерения площади равна сумме дисперсий погрешностей уменьшаемого и вычитаемого:

D[ A ] = D[ A N ] + D[ A b ]. (8)

Дисперсия площади, связанная с погрешностями вычисленной суммы откликов, может быть оценена через погрешности отдельных измерений:

D[ A N ] = ∑D[ y i ] = σ N ² ∙N . (9)

Большинство методов сглаживания сохраняют величину A_N неизменной. Эту часть погрешности можно оценить, но нельзя уменьшить линейными методами фильтрации шумов. Причиной этого является тот факт, что величина нулевого момента M 0 зависит только от исходных данных и остается почти неизменной при применении любого варианта взвешенного среднего.

Дисперсию площади под базовой линией (вычитаемое формулы (6) в отсутствие сглаживания можно оценить как

D[ A b ] = N ² ∙σ N ² / 2. (10)

Обратим внимание, что дисперсия суммы точек AN пропорциональна ширине пика, а дисперсия площади под базовой линией Ab — квадрату ширины, их отношение — N / 2. При оценке суммар- ной погрешности при N > 20 дисперсией площади D[AN] по сравнению с величиной D[Ab] можно пренебречь.

При применении линейной процедуры сглаживания одновременно увеличивается число точек N , относящихся к области пика, с N 0 до N , т.е. растет ширина пика и уменьшается погрешность оценки начальной и конечной точек базовой линии. Попытаемся найти минимум абсолютной погрешности площади трапеции (формула 7), соответствующей базовой линии. Для гауссового пика и га-уссового фильтра число точек, относящихся к пику, растет пропорционально квадратному корню из суммы вторых моментов исходного пика M 2 _p и щели сглаживания M 2 f :

N = N 0 ∙ (( M 2 p + M 2 f ) / M 2 p ) ^1/2 , (11)

а погрешность сомножителя ( B 1 + B 2) / 2 равна

D[( B 1 + B 2) / 2] = σ N ² / 2 K f = σ N ² / (2 k∙M 2 p ^1/2 ). (12)

Введем переменную s = M 2 f ^1/2 , обозначающую стандартное отклонение сглаживающей функции. Дисперсия площади под базовой линией A b равна

D[ A b ] = N²∙ D[( B 1 + B 2) / 2] =

= N 0² ∙σ N ² ∙ (1 + M 2 f / M 2 p ) / K f =

= N 0² ∙σ N ² ∙ (1 + s ² / M 2 p ) / (2 k∙s ) =

= N 0² ∙σ N ² ∙ (1 /s + s / M 2 p ) / 2 k .           (13)

Минимум этой функции по s достигается в точке, в которой производная выражения в скобке равна нулю d (1 / s + s / M2p) / ds = 0, –1/s2 + 1 / M2p = 0, s2 = M2p

или, другими словами, в точке минимума второй момент фильтра равен второму моменту сглаживающей функции. Таким образом, поскольку s ² = M 2 f — это второй момент фильтра, минимальная погрешность площади под базовой линией достигается при равенстве вторых моментов пика и фильтра или, другими словами, при одинаковой их ширине. В случае площади положение минимума абсолютной и относительной погрешностей совпадают в силу неизменности площади пика при сглаживании.

Погрешность высоты пика

При сглаживании пика линейным фильтром с положительными весами его высота получает систематическую ошибку — она уменьшается. Если как сам пик, так и сглаживающая функция имеют форму гауссианы, то в силу неизменности площади гауссианы при сглаживании высота изменяется как h ≈ h 0 ∙ ( M 2 p / M 2 ) ^1/2 .

Даже при наличии систематического искажения высоты пика ее можно использовать для расчета количества вещества, если алгоритм сглаживания идентичен при градуировке и анализе. Оценка абсолютной погрешности высоты на сглаженной хроматограмме складывается из погрешностей базовой линии и погрешности определения отклика вблизи вершины. Относительная погрешность высоты сглаженного пика оценивается выражением

D( Y i / h ) ≈ D( Y i / ( h 0 ∙ ( M 2 p / M 2) ^1/2 ) ≈

≈ 1.5 ∙σ N ² / ( K f h 0² ∙ ( M 2 p / M 2)) =

= 1.5 ∙σ N ² ∙h 0^–2 ∙ (1 + M 2 f / M 2 p ) / K f , (15) содержащим тот же сомножитель, что и площадь (уравнение 13): (1 + M 2 f / M 2 _p ) / K f . Положение минимума и аналогично случаю площади оптимальный фильтр оказывается таким, для которого второй момент фильтра равен второму моменту сглаживающей функции.

МОДЕЛИРОВАНИЕ СИГНАЛА

В качестве объекта моделирования мы выбрали отдельный пик гауссовой формы. Стандартное отклонение гауссианы, описывающей пик, равно σ p = 4.0 единиц оси абсцисс, высота пика H = 10 ⁵ единиц оси ординат. Ширина пика по основанию составляет для гауссианы 4 σ p = 16, что, в соответствии с данными вышеприведенной таблицы, допускает использование аппроксимационных методов оценки высоты пика. Для получения статистически значимых результатов смоделирована двухканальная хроматограмма с одной тысячей таких пиков на каждом канале, расстояние между пиками равно 100.001 единиц оси абсцисс. К одному из каналов добавлен нормальный некоррелированный шум с σ N = 3333 единиц оси ординат, что по формальным критериям [9] соответствует отношению сигнал/шум s / n = 10. Обратим внимание на принципиальную разницу между стандартными отклонениями пика σ p и шума σ N . Стандартное отклонение пика σ p = M 2 ^1/2 характеризует его протяженность по оси абсцисс, а стандартное отклонение шума относится к оси ординат. Разметка хроматограммы на пики производилась по каналу без шума, в область пика входили все точки, отклик в которых был отличен от нуля. Индексы точек границы пиков считались одинаковыми для двух каналов, базовая линия индивидуальна для каждого канала и для канала с наложенным шумом проведена, как показано на рис. 2. Расчет площадей и высот производился по каналу с шумом. Обработка данных производилась в программе "МультиХром" [6].

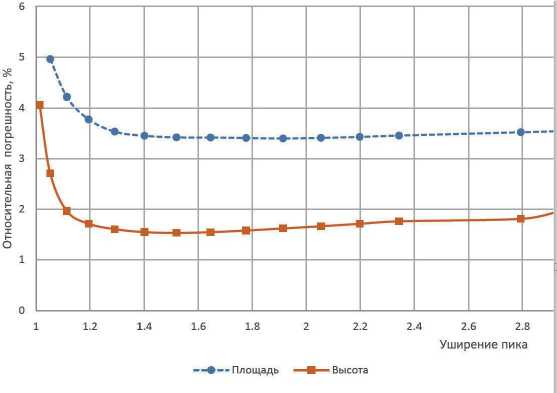
Рис. 3. Зависимость относительной случайной погрешности площади и высоты при сглаживании гауссианы гауссовым фильтром от сопутствующего сглаживанию уширения пика

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

На рис. 3 отображена зависимость случайной составляющей относительной погрешности площади и высоты пика, вычисленная по модельной хроматограмме с тысячей пиков, от его уширения. Как и ожидалось, графики имеют форму с характерным минимумом, ширина минимума больше для площади, чем для высоты. Точка √2 ≈ 1.4 в обоих случаях находится в области минимума. Данный график демонстрирует как эффект минимизации погрешности площади и высоты пика, так и побочный эффект такой оптимизации — уширение пика. Из рис. 3 следует, что применение окон фильтра более широких, чем сам пик, не имеет смысла, поскольку погрешность оценок площади и высоты существенно не улучшается, а ширина сглаженного пика растет (и высота соответственно падает). Погрешность высоты пика оказывается ниже ожидаемой по статистическим оценкам, поскольку в программе "МультиХром" при оценке высоты производится аппроксимация вершины параболой с параметрами, зависящими от ширины конкретного пика, что уменьшает суммарную погрешность оценки высоты. На выводы данной работы это влияния не оказывает, поскольку погрешность оценки положения базовой линии остается неизменной.

Появление оптимума параметров фильтра было отмечено в книге [15], правда, в ней не приводилось анализа причин появления этого оптимума и параметров фильтра, при котором оптимум достигается.

Площадь и высота модельного гауссова пика может быть измерена с низкой относительной погрешностью, но при этом высота оказывается в √2 раз ниже исходной, ширина растет во столько же раз. Разрешение между пиками падает так же, как растет их ширина — в √2 раз.

Если форма пика описывается ЭМГ, то после сглаживания гауссовым фильтром пик остается экспоненциально модифицированной гауссианой с неизменным параметром τ и изменившейся шириной гауссианы, коэффициент асимметрии при этом падает, т.е. пик становится более симметричным. Несимметричные нецентрированные фильтры, такие как экспоненциально взвешенное скользящее среднее, применять нежелательно, поскольку помимо уширения и сдвига положения первого момента они искажают симметрию пика, преобразуя, к примеру, симметричный гауссов пик в несимметричную экспоненциально модифицированную гауссиану.

Таким образом, в случае фильтрации шума симметричным линейным фильтром с неотрицательными коэффициентами платой за улучшение воспроизводимости базовых параметров пика является изменение всех валидационных параметров. В некоторых случаях такой подход может быть оправдан и весьма полезен, особенно в случаях хорошего разрешения между пиками, например в капиллярном электрофорезе.

Напомним, что в случае линейных фильтров сигнал и шум можно фильтровать независимо друг от друга, результат фильтрации сигнала даст систематическую составляющую погрешности, а шума — случайную. Посмотрим на результат приме- нения фильтров к сигналу без шума, отражающий систематическую погрешность сигнала. На рис. 4 изображены исходная гауссиана (сплошная кривая), результат применения к ней оптимального фильтра (штриховая линия) и результат применения фильтра Савицкого—Голея с таким же коэффициентом шумоподавления, как у оптимального гауссова фильтра (пунктир). Видно, что фильтр Савицкого—Голея заметно искажает исходный пик. Искажение площади оценить сложно, поскольку непонятно, каким образом ее мерить (где базу делать будем?). Если провести "истинную" базовую линию, расширив область пика за пределы провалов, в силу конструкции метода скользящего среднего площадь пика будет в точности равна площади исходной гауссианы. Высота сглаженного пика составила 65 % от исходной и появились провалы до и после пика глубиной 4.3 % высоты исходного пика. Высота даже меньше, чем у оптимально сглаженной гауссианы, где она составляет 71 % от исходной.

Сглаживание гауссианой позволяет достичь большего коэффициента шумоподавления, чем метод Савицкого—Голея, за счет более предсказуемого характера уширения пиков. Подбор оптимального окна фильтра Савицкого—Голея может быть произведен по нашей методике, разработанной для нелинейных фильтров [16]. Указанная методика позволяет выбрать максимальный размер окна, не приводящий к существенному изменению формы пика, и в этом случае в работе [16] показано, что фильтр Савицкого—Голея обеспечивает лучшее шумоподавление, чем фильтр Гаусса.

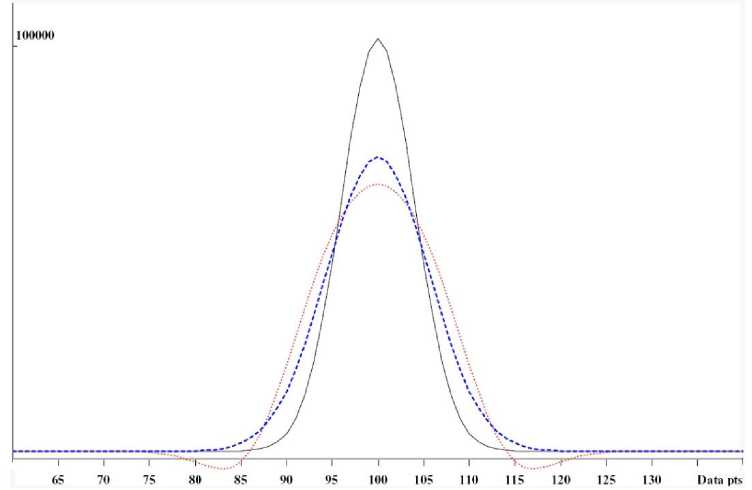
Рис. 4. Иллюстрация систематических искажений формы пика при сглаживании. Исходная гауссиана без шума (сплошная линия); гауссиана, к которой применен оптимальный фильтр Гаусса (штриховая линия); фильтр Савицкого—Голея (пунктирная линия), дающий такое же подавление случайной составляющей погрешности, как оптимальный фильтр Гаусса

Из изложенного следует, что причиной эффекта улучшения оценки площади при фильтрации шумов является более точное проведение базовой линии. Поэтому для получения минимальной погрешности площади следует уделять большее внимание фильтрации шумов не в области пика, а в области, где пиков нет, т.е. на базовой линии. В случае высоты погрешность базовой линии не столь значима, но характер зависимости погрешности от параметра фильтра оказывается таким же, как и для площади, и положение минимума относительной погрешности тоже приходится на случай одинаковых ширин пика и фильтра. Для узких пиков оценку высоты произвести затруднительно, но поскольку аппроксимационная оценка параметров проводится после сглаживания, то оказывается допустимой ширина несглаженного пика по основанию десять точек (10√2 ≈ 14, см. таблицу).

Подходы, связанные с уточнением положения базовой линии, разрабатывались нами в рамках он-лайн фильтрации шума без явного применения фильтров [17], через аппроксимацию точек начала и конца пиков. При такой аппроксимации не достигается минимальная погрешность проведения базовой линии и не уменьшается отношение сиг-нал/шум в соответствии с формальными критериями. Указанные недостатки преодолены в разрабатываемых нами адаптивных фильтрах, основанных на минимизации доверительного интервала аппроксимации в каждой точке обрабатываемого массива данных [16, 18]. Так, для приведенного в данной работе примера для одного из вариантов адаптивных фильтров случайная погрешность площади составляет 2.5 %, а погрешность высоты 1.9 %, т.е. погрешность площади меньше, а высоты больше, чем в случае оптимального гауссова фильтра, но при этом систематическое изменение высоты не превышает 1 %. Улучшение показателей по площади связано с тем, что коэффициент подавления шума базовой линии K f адаптивного фильтра для данного примера приблизительно в 1.9 раза выше, чем K f оптимального сглаживания гауссианой. Относительно высокая погрешность высоты связана с тем, что шумоподавление адаптивного фильтра внутри пика ниже, чем на базовой линии, поскольку перед адаптивным фильтром стоит задача сглаживания с сохранением формы пика. Напомним также, что вычислительная сложность и требования к оперативной памяти адаптивного фильтра существенно превышают таковые для сглаживания гауссианой, поэтому возможность его применения в микропроцессорной технике вызывает сомнения.

В данной работе не ставилась задача поиска оптимального алгоритма сглаживания, поставленная задача гораздо скромнее: выяснить оптималь- ные параметры симметричных линейных фильтров с неотрицательными коэффициентами. Оценки, подобные приведенной в данной работе, не встречались нам в литературе. Скользящее взвешенное среднее весьма популярно, требует малых вычислительных затрат, и выбор правильного размера окна фильтра гарантирует оптимальный результат, если конкретная аналитическая система обеспечивает избыточное разрешение пиков. Кроме того, при сравнении разных методов сглаживания появляется результат, на который можно ориентироваться.

ЗАКЛЮЧЕНИЕ

• •    Разработана модель формирования относительной погрешности высоты и площади пика.

• •    Показано, что погрешность оценки площади пика происходит главным образом от погрешности проведения базовой линии.

• •    Показано, что существуют параметры, при которых линейный фильтр c неотрицательными коэффициентами обеспечивает оптимальную относительную погрешность высоты и площади пика, причем второй момент фильтра близок ко второму моменту пика.

• •    Теоретические выкладки подтверждены численным моделированием сглаживания гауссова пика гауссовым фильтром.

• •    Проведено сравнение результатов численного моделирования с результатами альтернативных способов сглаживания.

Автор приносит свою благодарность Юрию Петровичу Козьмину и Андрею Сергеевичу Самохину за ценные советы по тексту статьи.

Данная работа не была поддержана никакими грантами