Оптимизация параметров низкоэнергетического сильноточного электронного пучка для эффективной транспортировки его в аргоне при низком давлении

Основной областью применения низкоэнергетических сильноточных электронных пучков (НСЭП) является модификация поверхностных слоев материалов. Преимущество таких пучков заключается в их способности без существенных потерь переносить энергию на достаточно большие расстояния и эффективно передавать ее объекту воздействия. Трудности, возникающие при транспортировке пучка, обусловлены образованием виртуального катода при неполной нейтрализации пучка, который запирает пучок на входе в пространство дрейфа. При полной зарядовой нейтрализации опасность потери тока вызывает самопинчевание пучка в собственном магнитном поле. Поэтому при транспортировке следует обеспечить полную нейтрализацию пучка, а эффект самопинчевания ослабить за счет внешнего магнитного поля. Возникает проблема хорошей воспроизводимости пучка с заданными параметрами, а также возможности управления параметрами пучка. Сложность этих задач обусловлена тем, что процесс формирования и транспортировки пучка электронов осуществляется в сильном электрическом и магнитном полях пучка, которые существенно зависят от проводимости плазмы, создаваемой самим пучком [1]. Поэтому, учитывая изложенное выше, очень важно найти оптимальные параметры системы.

Целью данной работы является оптимизация параметров пучка для эффективной транспортировки его к мишени. В качестве параметров использовались максимальное значение тока пучка, длительность импульса, радиус пучка и давление газа. В качестве критериев оптимизации были приняты наибольшее значение плотности ионов на оси и минимальная плотность полного тока на оси. Для определения оптимальных параметров ионизации был выбран метод Нелдера – Мида, при использовании которого не требуется вычислять градиент функции. Все вычисления проводились в пакете Matlab, содержащем реализованный метод Нелдера – Мида. Для ускорения поиска оптимальных параметров применялось распараллеливание.

При использовании электронного пучка в нанотехнологии его транспортировка осуществляется в пространстве дрейфа, заполненном аргоном, при давлении 0,13 - 13,3 Па. За время, много меньшее длительности фронта пучка, происходит ионизация газа и образуется плотный плазменный канал, по которому распространяется электронный пучок. Ионизация газа в пространстве дрейфа происходит как за счет ударной ионизации быстрыми электронами пучка, так и за счет полей, наводимых на фронте пучка. В зависимости от давления, геометрии камеры дрейфа и параметров пучка изменяются параметры плазменного канала, такие как плотность электронов, температура и проводимость плазмы, что в свою очередь приводит к изменению токовой нейтрализации пучка и условий его транспортировки. Математическая модель формирования плазменного канала в указанных условиях представляется в виде системы уравнений (цилиндрическая система координат ( r , ф , z )) [2]

1 д( дA )    4л, х

-—I r— 1 =--(jbz + jpz),

r д r V д r ) c

1 дjpz Def д t pz

д T e д t

2 e ² E ² c ²

eVef ( Te - Ta )=T----Г---, 3 mec V ef д n^1 д t

= ^ivbnbng + neKng - Kkn^ng - «r 1 n^ne - «r2nf’neng - «r3n^ ne , д n (2) д t

= Kkn,(1)n2 - an-2)n, g r e где   Az   – векторный потенциал поля с нулевыми граничными условиями:

д A z д r

= 0, r=0

Az |_r = R = 0 ; R_c — радиус трубы дрейфа; j_bz = ev_bn_b - плотность тока пучка; j pz -

плотность плазменного тока; vf = 1,3-109pTe + 2,86-10 5n Te 1,5 - эффективная частота столкно- ne2

вений электронов плазмы с тяжелыми частицами; с т = ^e /, _х - проводимость плазмы; / ( m e ^V ef )

2 e ² T    p ² c ²

газа; х =—^e— e

3 m e c V ^2.8 ) ^Te v ef

а                            б                             в

F n • IO ¹⁴ , мкс                                   F n • IO ¹³ , мкс                                F n • IO ¹³ , мкс

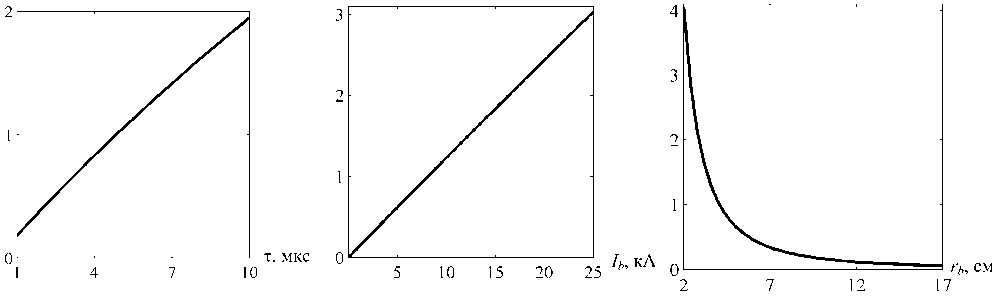
Рис. 1. Зависимость максимальных значений плотности ионов на оси от параметров T (а), Ib (б), rb (в) пучка

на; a i - сечение ионизации; n g = 3,5 - 10 16 p - n i - плотность газа; K i - постоянная ионизации;

Kk - коэффициент конверсии; ar 1, ar2,ar3, a rd - коэффициенты рекомбинации; n^\n^ - плот ность атомарных и молекулярных ионов аргона соответственно; пе = ni - nb - плотности электронов пучка; ni = n^ + n^2). Предполагается цилиндрическая симметрия процесса. В случае коротких труб дрейфа, когда время пролета пучка этой трубы значительно меньше длительности его импульса, зависимостью от z можно пренебречь.

Вычисления будем проводить для пучка с радиусом rb = 3 см, энергией 20 кэВ, максиму мом тока Ib = 15 кА, длительностью импульса т = 1 мкс. Труба дрейфа радиусом 9 см заполнена ионизованным аргоном, находящимся под давлением p = 2,66 Па. Считаем, что пучок имеет полную зарядовую нейтрализацию.

Рассмотрим критерий максимизации плотности ионов

Gn = max [ Fn (k )], Fn (k ) = max (n( r = 0, t, k )).

Сначала определяется временная зависимость плотности ионов на оси, затем вычисляется максимум этой зависимости F_N . Эта процедура повторяется для заданного параметра k . В результате получаем набор значений F_N ( k ) (рис. 1), после чего определяется максимум этого набора

G_N . На рис. 1 видно, что для всех параметров пучка функция не имеет экстремумов. Метод

Нелдера – Мида также не позволяет обнаружить их на заданных интервалах. В случае, когда па- раметром является длительность импульса, очевидно, что чем она больше, тем выше плотность ионов в конце импульса. Поэтому целесообразно нормировать функцию на величину длительности импульса. Аналогичное действие нужно выполнить для тока пучка. Следует отметить, что при других значениях давления газа характер кривых на рис. 1 качественно не меняется.

На рис. 2 представлены графики нормированного критерия

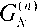
= max [ Fⁿ ) ( k ) ] , F n n ) ( k ) =

max

^ n i ( r = 0, t , k p

v      T Ib      >

а                                                б

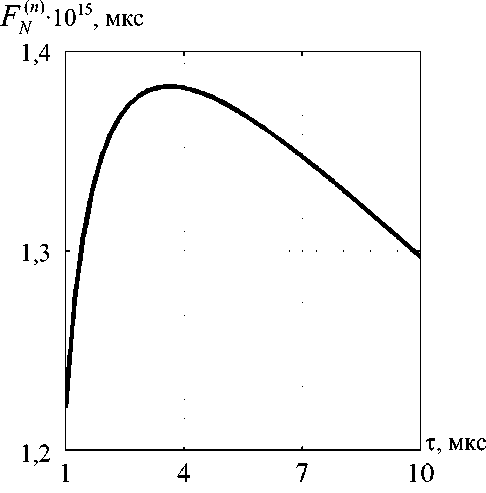
Рис. 2. Зависимости максимальных значений плотности ионов на оси, нормированных на длительность импульса и максимум тока пучка, от различных параметров Т ( а ), I_b ( б ) пучка

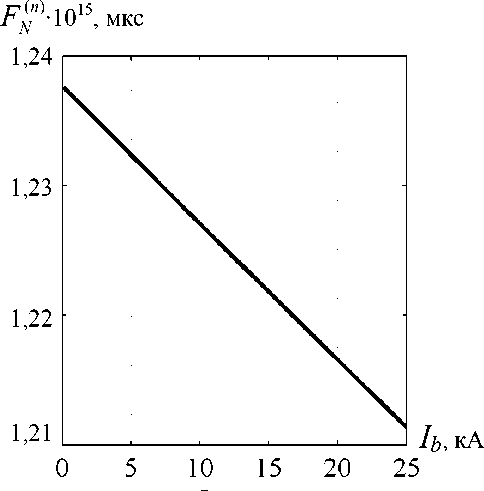
Видно, что функция F Nn ) ( k ) имеет экстремум. Проверка, выполненная с помощью метода Нелдера – Мида, подтвердила полученный результат. В данном случае точка оптимума соответствует длительности импульса т = 3,6365 мкс.

Рассмотрим критерий плотности полного тока (рис. 3):

G j = min [ F j ( k ) ] , F j ( k ) = max ( j b^ ( r = 0, t , k ) + j p _3Z ( r = 0, t , k ) ) .

Во всех случаях экстремум не обнаружен, что подтверждает метод Нелдера – Мида.

Следует отметить, что при нормировке в указанных выше случаях оптимальные экстремумы не были найдены. Например, при

G ^{( n )} = min [ F ⁽ n ⁾ ( k ) ] , F ⁽ n ⁾ ( k ) = max [ ^{jbz (} r = 0’ t , k ^{) +} j ^z ⁽ r = 0, t , k )'

L J                  I              Tib              J получаем результат, представленный на рис. 4.

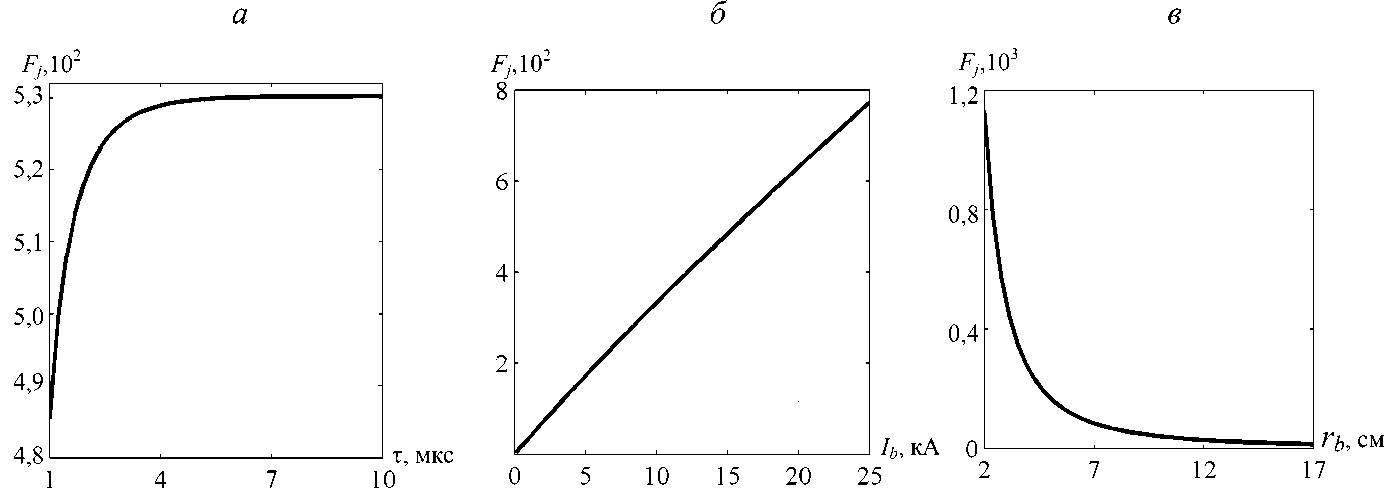
Рис. 3. Зависимости максимальных значений плотности полного тока на оси от параметров T ( а ), I b ( б ), r b ( в ) пучка

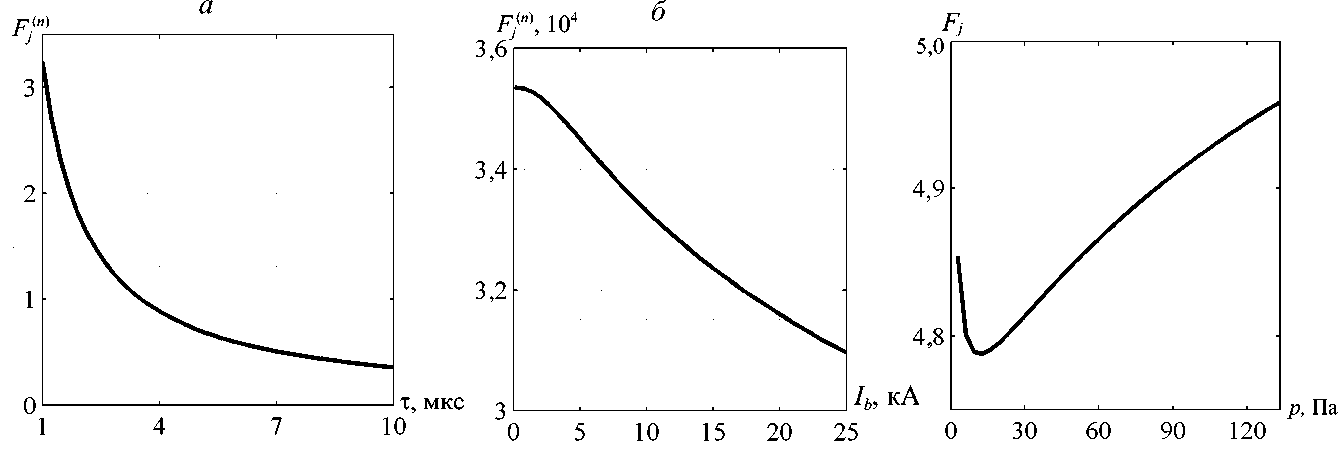
Рис. 4. Зависимости максимальных значений плотности значений плотности полного тока на оси от давления газа полного тока на оси, нормированных на длительность импульса и максимум тока пучка, Т (а), Ib (б) пучка

Рис. 5. Зависимость максимальных

Если в качестве параметра используется давление, то в случае критерия минимальности G_j экстремум будет существовать ( p = 12,7 Па ) , и он будет оптимальным (рис. 5).

На рис. 6 видно, что одновременное использование двух полученных выше оптимальных параметров (давления газа и длительности импульса пучка) не обеспечивает выполнение критерия минимума плотности полного тока, в то время как из рис. 7 следует возможность выполнения критерия нормированной плотности ионов.

В работе рассмотрены широкие диапазоны параметров с целью более полного анализа математической модели. Вследствие недостатка точек оптимума отсутствует возможность искать экстремум сразу по двум параметрам. Установлено, что оптимальный минимум

а

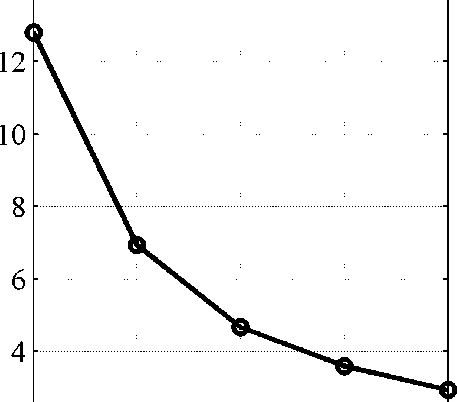
2------------1------------'------------1------------т, мкс

1,0 1,5 2,0       2,5 3,0

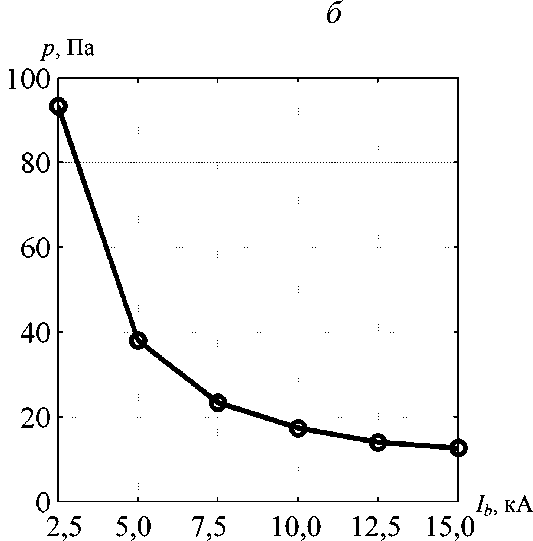
Рис. 6. Зависимости между параметрами, при которых достигаются оптимальные значения критерия минимума плотности полного тока:

а - Р ( ^Т ) ; б - Р ( I b )

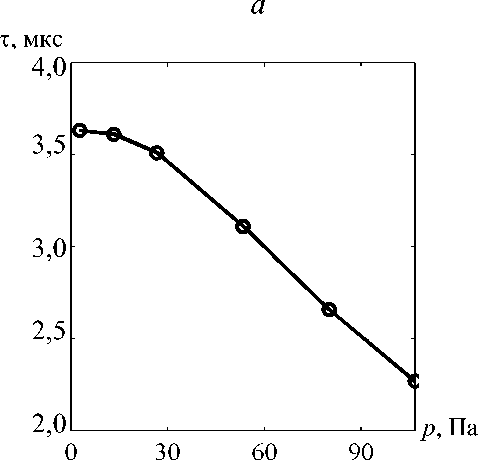
Рис. 7. Зависимости между параметрами, при которых достигаются оптимальные значения критерия максимума нормированной плотности ионов:

б

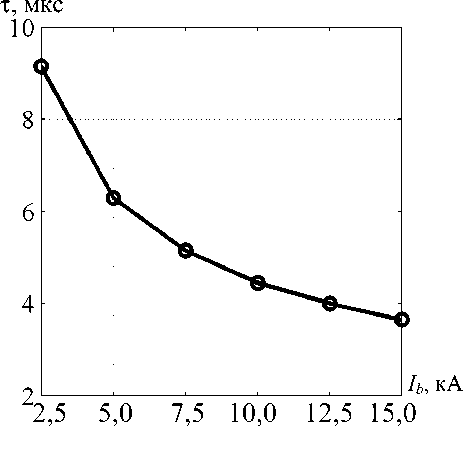
а - ^т ( p ) ; б - т ( I b )

плотности полного тока имеет место при давлении p = 12,7 Па, а оптимальный максимум нормированной плотности ионов достигается при длительности импульса пучка т = 3,6365 мкс.