Оптимизация параметров планарной бинарной линзы для видимого диапазона излучения

Актуальной задачей является уменьшение диаметра фокусного пятна фокусирующей системы. Например, в работах [1 –4] использовались бинарные и полутоновые дифракционные элементы, дополняющие основной объектив. В этих работах использовался радиально-поляризованный свет. В [5] для получения острой фокусировки света с целью достижения нанотурбулентностей в жидкостях использовались микродиски. Диски из нитрида кремния Si3N4 (показатель преломления n = 2,1) высотой 400 нм и диаметром от 1 до 10 мкм облучались светом с длиной волны 488, 532 и 633 нм. В работе достигнута фокусировка света внутри диска в фокусное пятно овальной формы по полуспаду интенсивности FWHM=460 нм, то есть 0,72λ в лучшем случае. При моделировании в [6] достигнута фокусировка света в пятно шириной 0,4λ. Для этого использовалась градиентная 3D линза Микаэляна, фокусирующая радиально-поляризованный свет, максимальный показатель преломления в центре линзы n = 1,5. Моделирование проводилось с помощью FDTD – метода. В [7] было получено изображение точечного источника света с помощью градиентной 2D микролинзы Микаэляна с максимальным показателем преломления в центре линзы n =3,47 (кремний) для длины волны света λ = 1,55 мкм. Ширина максимума интенсивности по полуспаду составила FWHM=0,12λ. А в [8] с помощью дифракционного элемента с числовой апертурой NA=0,95 удалось сфокусировать радиально-поляризованный свет в пятно шириной FWHM=0,7λ. Как видно из приведённых работ, наилучшая фокусировка света FWHM=0,12λ достигнута при использовании 2D градиентной линзы с максимальным показателем преломления в центре n =3,47, что соответствует кремнию. Для показателя преломления в центре линзы n = 1,5 достигнута фокусировка света диаметром не менее 0,4λ. Кремний пропускает свет с длинами волн от 1,2 мкм до 7 мкм, при этом при прохождении светом 10 мм в кремнии наблюдается его затухание вдвое [9], что делает его удобным для изготовления оптики для телекоммуникационной дли- ны волны света (λ = 1,55 мкм) и практически невозможным его использование для линз, работающих в видимой области спектра. Однако для изучения свойств градиентных линз удобно использовать лазерное излучение с длиной волны λ =532 нм. Эта длина волны соответствует зелёному цвету видимой части спектра и может быть сгенерирована полупроводниковым лазером, а также твёрдотельным лазером на неодимовом стекле (с двукратным умножением основной частоты). У этих лазеров высокий КПД и видимое глазом и CCD– камерами излучение, они широко распространены и относительно дёшевы.

В данной работе проведено 3D моделирование фокусировки линейно-поляризованного света планарной бинарной микролинзой или фотонно-кристаллической (ФК) линзой, аналогичной градиентной линзе Микаэляна для длины волны света λ = 0,532 нм. Фотонные кристаллы использовались для фокусировки света и ранее, например в [11] моделировалась фокусировка световых импульсов многослойным фотонным кристаллом, однако полученное фокусное пятно было порядка длины волны света 1,55 мкм. Кроме того, фотонный кристалл в [11] не рассчитывался как аппроксимация градиентной секансной линзы.

Предполагается, что линза, рассчитанная в данной работе, выполнена в плёнке электронного резиста, имеющего показатель преломления n = 1,56, нанесённого на подложку из плавленого кварца ( n 0 = 1,46). Такой вариант моделирования линзы выбран потому, что возможно изготовление такой линзы средствами электронной литографии. Моделирование проводилось FDTD-методом, реализованным в программе FullWave фирмы RSoft.

Моделирование в двумерном случае

Для начала рассмотрим двумерный вариант. На рис. 1 приведена схема рассматриваемой задачи в 2D случае. Свет с длиной волны λ =532 нм распространяется в планарном волноводе шириной W и фокусируется градиентной секансной линзой. На линзу падала плоская волна с ТЕ-поляризацией. Вектор электриче- ского поля направлен вдоль оси Y. Волноводом является плёнка электронного резиста, нанесённая на плав-лёный кварц. Показатель преломления резиста n1= 1,56. Для удобства изготовления линза выполнена в виде фотонного кристалла (ФК). Градиентный показатель преломления в линзе [6] формируется за счёт травления отверстий в электронном резисте до подложки. Линза рассчитывалась в предположении возможности изготовления средствами электронной литографии с разрешением 100 нм.

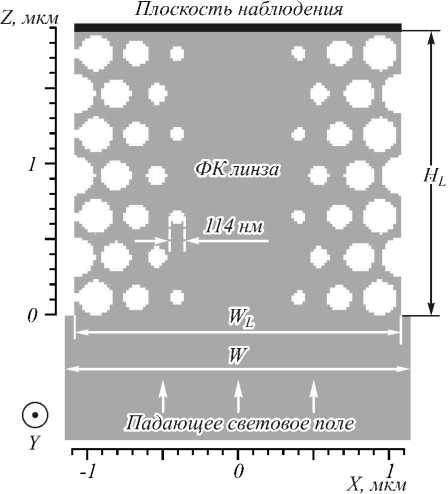
Рис. 1. Схема рассматриваемой задачи в двумерном случае (серый цвет – n = 1,56, белый – n = 1)

Минимальный диаметр отверстия в градиентном фотонном кристалле, образующем линзу, равен 114 нм. Показатель преломления подложки n ₀ = 1,46. Для получения острой фокусировки света на границе ФК линзы её ширина была выбрана W_L = 2,55 мкм, длина H_L = 1,83 мкм. При таких параметрах в двумерном случае ширина фокусного пятна по полуспаду интенсивности составила FWHM=0,361λ, эффективность фокусировки по полуспаду интенсивности составила 65%. Расположение и диаметр отверстий в ФК были рассчитаны для данных параметров ширины и высоты линзы, после чего была проведена оптимизация величин W_L и H_L с целью уменьшения фокусного пятна. Для ускорения расчётов оптимизация размеров ФК линзы была проведена в двумерном случае для ТЕ-поляризации.

При изменении ширины W_L и высоты H_L линзы координаты центров отверстий сдвигались пропорционально, но их диаметры оставались неизменными. На рис. 2 представлены графики распределения интенсивности излучения в плоскости наблюдения в 10 нм за линзой до и после оптимизации.

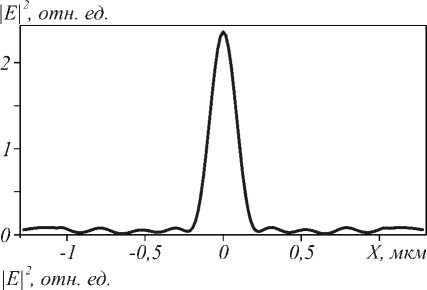
При начальных расчётных параметрах в плоскости наблюдения имеется только фокусное пятно практически с полным отсутствием боковых лепест- ков (рис. 2а). Однако при некотором появлении боковых лепестков (их высота составляет около 30% от основного максимума интенсивности) можно уменьшить ширину фокусного пятна. Минимальная ширина фокусного пятна (рис. 2б) FWHM=0,28λ и достигается при ширине и высоте линзы WL = 2,652 мкм, HL = 1,39 мкм (рис. 3). Эффектив- ность фокусировки при этом упала до 39,8%.

б)

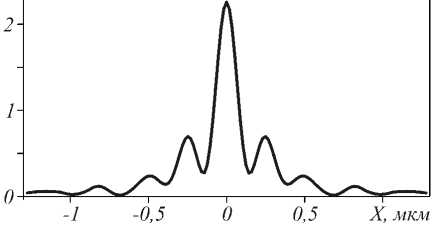
Рис. 2. Распределение интенсивности в 10 нм за линзой в двумерном случае до оптимизации (а) и после оптимизации (б) размеров линзы. Падающая на волновод плоская волна, интервал разбиения сетки отсчётов по всем трём координатам равен λ/30

Оптимизированный профиль показателя преломления линзы показан на рис. 3.

Z, л/юи-

X, мкм

-10   1

Рис. 3. Распределение показателя преломления в линзе в плоскости XZ после оптимизации ширины и высоты (серый цвет – n=1,56, белый цвет – n=1)

Наибольшее значение для получения острой фокусировки имеет часть света, падающего на края линзы. Если линза освещается светом с гауссовым распределением интенсивности с радиусом σ вдоль оси X, равным половине ширины линзы, острота фокусировки падает значительно. На рис. 4 пред- ставлено распределение интенсивности поля на расстоянии 10 нм за линзой для гауссова источника света с радиусом вдоль оси X σ = 1,275 мкм в двумерном случае. Для рис. 4 ширина фокусного пятна FWHM = 0,35 λ, что примерно на 30% больше, чем в случае плоской падающей волны. Однако в волноводе с постоянным показателем преломления устанавливается основная мода с почти гауссовым распределением интенсивности. Для увеличения интенсивности падающего света на края линзы ширина волновода W была выбрана больше ширины линзы, а радиус гауссова пучка вдоль оси X был принят σ = 2,75. Таким образом, на линзу попадает центральная часть гауссова пучка, амплитуда которого на краях линзы падает приблизительно до 0,8 от максимума по центру линзы. Это улучшает остроту фокусировки, хотя и уменьшает её эффективность.

|Е|\ опт. ед.

1,2

1,0

0,8

0,6

0,4

0,2

О

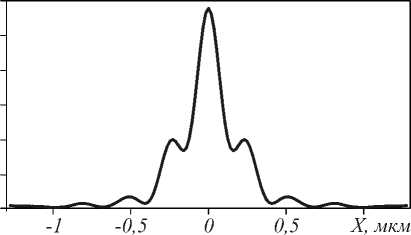
Рис. 4. Распределение интенсивности за линзой, освещённой гауссовым пучком с радиусом вдоль оси X σ=1,275 мкм в двумерном случае, W=WL

Моделирование в трёхмерном случае

Трёхмерная оптическая схема и внешний вид линзы с волноводом изображены на рис. 5. Ось Z проходит через оптическую ось системы – по центру планарного волновода (хотя на рис. 5 она нарисована сбоку).

Основной волновод шириной W продолжается по бокам линзы, при этом между ним и ФК-линзой имеются щели шириной x ₁ . Таким образом часть света, не попавшая на линзу, распространяется дальше за неё и может быть отведена по двум волноводам за пределы области фокуса. Моделирование показало, что в трёхмерном случае на ширину фокусного пятна ФК-линзы влияет как толщина плёнки волновода, так и величина зазора x ₁ по бокам линзы.

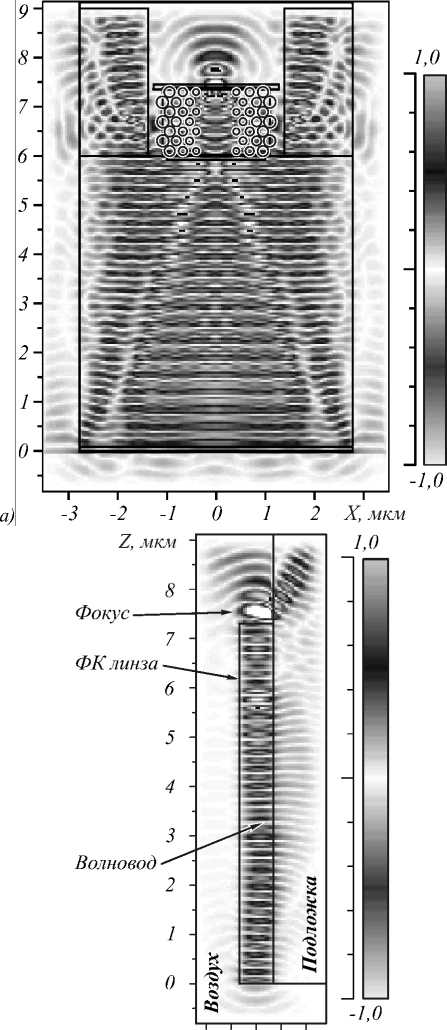
Моделирование трёхмерной оптической схемы проводилось при следующих параметрах: радиус распространяющегося в волноводе гауссова пучка σ = 2,75 мкм, длина волновода между источником и линзой L =6 мкм, ширина волновода W =5,5 мкм, интервал разбиения сетки отсчётов по всем трём координатам равен λ/20. Размеры линзы WL и HL те же, что и на рис. 4. На рис. 6 показаны мгновенные распределения амплитуды поля Ey в момент времени cT = 12 мкм, где c – скорость света в вакууме. Волновод освещён волной с напряжённостью электри- ческого поля Ey , а в фокусе линзы рассчитывалась интенсивность I = E2| = |Ey| + |Ez |2, где Ez - про- дольная составляющая электрического вектора.

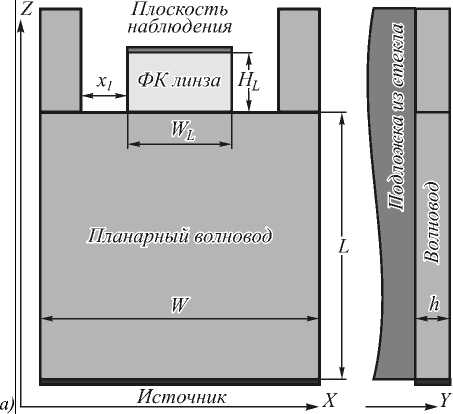
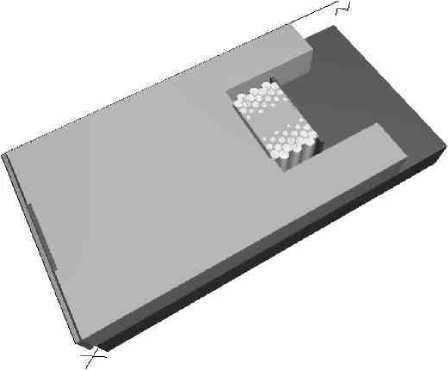
Рис. 5. Трёхмерная оптическая схема планарной ФК– линзы на подложке из плавленого кварца (а) и 3D вид (б)

Из мгновенных распределений поля E y видно, что после достижения конца линзы часть света переходит в подложку и начинает распространяться вглубь, другая часть выходит в окружающее пространство над подложкой. Также видно, что за счёт избыточной ширины W волновода по отношению к ширине линзы W_L на линзу попадает центральная часть из гауссова пучка в волноводе. За счёт этого достигается более равномерная интенсивность падающего поля как по центру, так и на краях ФК– линзы, что улучшает остроту фокусировки.

На рис. 7 а представлена зависимость ширины фокусного пятна по полуспаду интенсивности от толщины волновода, измеренная по центру волновода. Зазор по краям линзы при этом был принят x 1 =0,11 мкм.

Из рис. 7 а видно, что чем меньше толщина волновода h , тем шире фокусное пятно вдоль оси X . С другой стороны, чем меньше толщина волновода h , тем меньше доля света, распространяющаяся в плёнке волновода в виде моды.

Z, мкм

-1    0     1

б)                     Y. мкм

Рис. 6. Мгновенное распределение поля Ey в момент времени cT=12 мкм в плоскости XZ, Y=0 (а) и в плоскости YZ, X=0 (б), TE-поляризация

Зависимость максимума усреднённой по времени интенсивности в фокусе линзы от толщины волновода показана на рис. 7 б . Видно, что с уменьшением толщины волновода h менее 0,75 мкм интенсивность света в фокусе линзы падает, что свидетельствует о потере света, уходящего в подложку. Однако с увеличением толщины волновода увеличивается соотношение глубины травления к диаметру отверстий, составляющих фотонный кристалл (аспектное отношение), что усложняет изготовление ФК–линзы средствами электронной литографии. Оптимальным было выбрано значение высоты h =0,6 мкм.

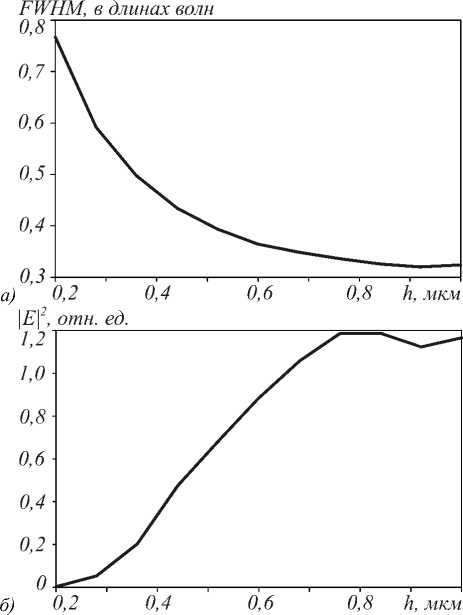
Рис. 7. Зависимость ширины фокусного пятна линзы от толщины плёнки волновода (а); зависимость величины максимума интенсивности |E|2 в фокусе от толщины волновода (б); x1=0,11 мкм для обоих графиков

На рис. 8 показана зависимость ширины фокусного пятна вдоль оси X через центр волновода по полуспаду интенсивности от расстояния x ₁. Видно, что наиболее оптимальное расстояние x ₁ = 0,11 мкм. При этом достигается минимальное фокусное пятно FWHM = 0,365λ и максимальная интенсивность в фокусе. Эффективность фокусировки по полуспаду интенсивности при этом равна 41%. При другой толщине волновода h меняется только интенсивность в фокусном пятне, оптимальное расстояние x ₁ остаётся постоянным.

На рис. 9 показана форма фокусного пятна за линзой при оптимальных параметрах: x ₁ = 0,11 мкм, h =0,6 мкм. Видно, что в трёхмерном случае боковые лепестки проявляются слабее (15%), чем в двумерном случае (30%), как в случае плоской падающей волны на линзу (рис. 2 б ), так и в случае гауссова распределения (рис. 4). Ширина фокусного пятна вдоль оси X FWHM=0,365λ.

Поскольку линза планарная, вдоль оси Y фокус не наблюдается, ширина по полуспаду интенсивности вдоль оси Y FWHM=0,74λ.

Если же убрать фотонный кристалл (заполнить отверстия тем же материалом), то фокус в плоскости наблюдения превращается в интерференционную картину, состоящую из трёх пиков интенсивности равной величины, причём центральный пик интенсивности становится шире, в этом случае его ширина FWHM=0,46λ. Это показано на рис. 10. Все остальные параметры моделирования те же, что и на рис. 9.

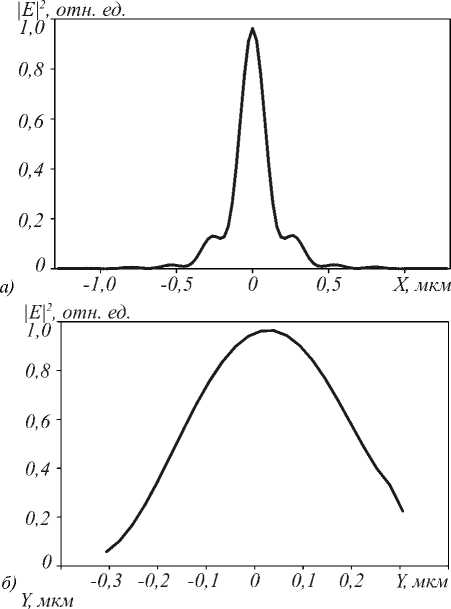
Рис. 9. Распределение интенсивности |E|2 за линзой по линии вдоль оси X через максимум интенсивности (по центру волновода) с ФК–линзой (а); вдоль оси Y через центр волновода (б); двумерное распределение интенсивности |E|2 в плоскости наблюдения (негатив) (в)

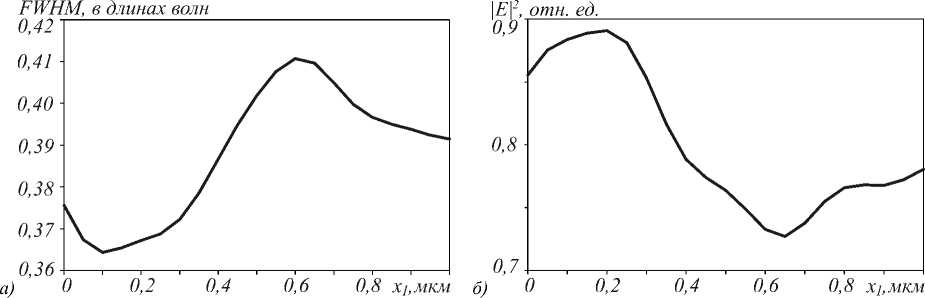
Рис. 8. Зависимость ширины фокуса FWHM вдоль оси X (а) и зависимость интенсивности |E|2 в центральной части фокусного пятна (б) от расстояния x1 между линзой и частями волновода вдоль линзы, толщина волновода h=0,6 мкм

Из рис. 10 также видно, что в случае отсутствия ФК–линзы несимметричность оптической схемы вдоль оси Y (наличие подложки с близким показателем преломления) сказывается на положении максимумов интенсивности, они смещены в сторону подложки примерно на 60 нм. При наличии фотонного кристалла, образующего линзу, этого эффекта не наблюдается.

Заключение

В работе получены следующие результаты:

|Е|-. отн. ед. 0,4

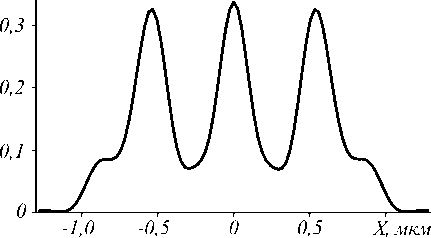
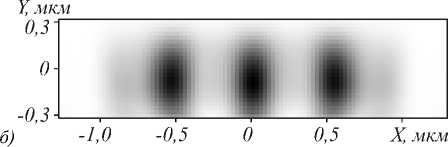
Рис. 10. Распределение интенсивности за линзой (|E|2) по линии вдоль оси X через максимум интенсивности (на расстоянии 0,24 мкм от подложки) без фотонного кристалла (отверстия отсутствуют) (а); двумерное распределение |E|2 в плоскости наблюдения (негатив) (б)

• •    Рассчитана цилиндрическая планарная бинарная линза, аналог градиентной линзы Микаэляна [6, 7], шириной W L = 2,652 мкм, длиной H L = 1,39 мкм, выполненная в виде фотонного кристалла в плёнке резиста с показателем преломления n 1 = 1,56 на подложке из плавленого кварца с показателем преломления n 0 = 1,46, которая фокусирует свет с ТЕ-поляризацией, λ =532 нм на своей границе с шириной по полуспаду интенсивности вдоль оси, поперечной волноводу, FWHM=0,28λ в двумерном случае и FWHM=0,365λ в трёхмерном случае; эффективность фокусировки света в трёхмерном случае равна 41%. Этот диаметр меньше, чем было получено для 3D цилиндрической линзы Микаэляна в [6], и меньше, чем диаметр фокусного пятна, полученный с помощью микросфер из латекса ( n = 1,59) диаметром 3 мкм [10].

• •    Показано, что за счёт изменения длины и ширины бинарной линзы от расчётных значений удалось уменьшить ширину фокусного пятна с FWHM=0,361λ до FWHM=0,28λ в двумерном слу-

• чае, при этом возникли дополнительные боковые лепестки рядом с основным максимумом интенсивности, составляющие 30% от основного максимума.

Работа выполнена при поддержке ФЦП «Научные и научно-педагогические кадры инновационной России» (госконтракт № 14.740.11.0016), грантов Президента РФ поддержки ведущих научных школ (НШ-4128.2012.9) и молодого кандидата наук (МК-3912.2012.2), а также гранта РФФИ № 12-07-00269.