Оптимизация параметров слоистых плит при динамическом проникании жесткого индентора с учетом трения и ослабляющего эффекта свободных поверхностей

Проблема ударного взаимодействия деформируемых тел представляет широкую область экспериментальных и теоретических исследований, некоторый подкласс которой составляют задачи оптимизации. Возможны различные постановки оптимизационных задач – оптимизация формы ударника, поиск оптимального распределения механических характеристик по толщине плиты, определение параметров разнесенной преграды и т.д. Задачи могут различаться по критерию качества – минимизация веса либо толщины преграды, способной обеспечить полную остановку ударника заданной формы и энергии; максимизация начальной скорости ударника, удерживаемого преградой; минимизация конечной скорости ударника после его полного пробития преграды.

Изучению процесса динамического проникания посвящено большое число работ, связанных с экспериментальными или численными исследованиями, аналитическими решениями. Классификация этих работ возможна не только по указанным выше критериям качества и геометрии ударника, но и по типу математической модели процесса и метода решения. Разнообразие моделей и методов связано с тем, что не существует единой схемы, с помощью которой возможно достаточно эффективно решить любую поставленную задачу из указанного класса.

В одной из первых моделей ударного внедрения жесткого осесимметричного тела в деформируемую преграду по нормали для удельной силы сопротивления внедрению о была принята эмпирическая зависимость [1,2], справедливая для условий вязкого образования кратера о= Hd + к ри2, (1)

где ρ, H d – плотность и динамическая твердость материала преграды; к - коэффициент формы головной части ударника; и - текущая скорость ударника. Слагаемые в соотношении (1) отражают собственное и инерционное сопротивление преграды.

Иной подход для определения силы сопротивления внедрению был предложен в работах Форрестола [3, 4], где движение ударника рассматривается на двух стадиях и на участке инерционного торможения силы сопротивления и в отличие от (1) описывается трехчленным выражением, в которое включается также и вязкостная составляющая.

В модели Сагомоняна [5] задача определения силы сопротивления, действующей на ударник, сводится к исследованию процесса расширения круговой цилиндрической полости в упруго-идеальнопластической несжимаемой среде. Этот подход позволяет аналитически получить выражение для давления, действующего на ударник, однако при довольно сильном допущении движение частиц материала преграды, соприкасающихся с поверхностью внедряющегося ударника, происходит в направлении, перпендикулярном направлению проникания. При таких допущениях решение ограничивается случаями проникания тонких заостренных тел вращения.

Ряд исследований посвящен задаче определения оптимальной формы внедряющегося тела. В работе [6] была поставлена задача оп- тимизации формы жесткого тела вращения, внедряющегося в деформируемую среду. Для описания процесса была использована двухстадийная модель, предложенная Форрестолом, критерием качества служила максимальная глубина проникания. В результате расчетов с помощью методов, основанных на генетическом алгоритме, получено, что оптимальный ударник имеет форму затупленного тела. В аналогичной постановке была рассмотрена задача для ударника, имеющего форму пирамидального тела, при ограничении на его объем [7]. Показано, что при одних значениях параметров задачи оптимальная форма ударника стремится к трехграннику, в других случаях максимальная глубина проникания отвечает круговому сечению ударника. Кроме того, были рассмотрены ударники, имеющие форму усеченных пирамидальных тел, и установлено, что небольшое усечение пирамидального ударника может увеличить глубину проникания.

Обзор [8] включает в себя свыше 50 работ, посвященных проблемам оптимизации форм внедряющихся тел. Сводка обозреваемых работ представлена в виде таблицы, в которой приведена классификация работ по моделям, критериям оптимизации, формам ударника и методам решения.

Выделим ряд работ, посвященных проблеме повышения защитных свойств неоднородных преград. В работе [9] экспериментально исследовалось проникание конического ударника в стальную преграду. Показано, что сопротивление прониканию монолитных плит выше слоистых при одинаковой общей толщине. Однако появление воздушных прослоек может повысить баллистическую сопротивляемость. Этот результат подтвержден и для алюминиевых преград авторами [10]. В экспериментальной работе [11] исследовалась перфорация стальных плит пулями и сравнивались между собой монолитные, слоистые и разнесенные преграды. Получено, что монолитные плиты эффективнее слоистых в баллистическом смысле. Кроме того, показано, что повышение числа слоев в преграде отрицательно сказывается на ее баллистической сопротивляемости.

В работе [12] доказано, что баллистические свойства преграды зависят от порядка расположения и толщины пластин, при этом эффект разнесения может привести как к повышению, так и снижению сопротивляемости преграды. В [13] численными методами авторами получен следующий результат: эффект расслоения может ослабить баллистические характеристики тонких и средней толщины преград по сравнению с их монолитными эквивалентами, однако на толстые преграды данный эффект влияет незначительно. Сравнительный анализ эффективности защитных свойств монолитных и разнесенных преград был проведен также в работе [14]. Задача динамического проникания алюминиевого цилиндра в диапазоне скоростей удара от 750 до 3000 м/c решалась в трехмерной постановке методом конечных элементов. Показано, что эффективность разнесенных конструкций возрастает с увеличением скорости взаимодействия и определяется характером разрушения в преградах. В работе [15] исследовался эффект воздушных прослоек в разнесенных преградах. Установлено, что в рамках модели локального взаимодействия баллистический предел разнесенных преград не зависит от воздушных прослоек и их ширины для конических ударников. Кроме того, в случае неконических ударников при данном эффекте величина баллистического предела подвергается малым изменениям.

В серии работ [16–18] авторами решалась следующая задача оптимизации: определить последовательность материалов и толщины слоев преграды, обеспечивающих максимальный баллистический предел. В работе [16] исследовался нормальный удар конического ударника в слоистую преграду, состоящую из пластин, в которых чередовались два заданных материала. Причем суммарная толщина пластин, изготовленных из каждого материала, считалась заданной величиной. Доказано, что оптимальная преграда является двухслойной, а также получен критерий, позволяющий определить один из двух возможных вариантов структуры в качестве оптимальной. Позже авторы получили правило определения последовательности пластин в оптимальной преграде для большего числа материалов. В работе [17] доказано, что это правило пригодно к использованию и для случая внедрения ударника с оживальной головной частью. В [18] была рассмотрена более общая постановка задачи определения последовательности материалов и толщин слоев в предположении существования ограничений на толщины пластин, а также верхнего ограничения на суммарную толщину всей преграды.

В работе [19] была поставлена задача оптимизации структуры защитной преграды заданной толщины, обеспечивающей максимум предельной баллистической скорости ударника. Решение задачи определялось выявлением последовательности укладки и толщины слоев для заданного набора материалов. Задача была решена с использованием эмпирической модели (1). Авторы получили аналитические выражения для предельной баллистической скорости, продемонстрировали способ получения оптимальной структуры защитной преграды, провели теоретическую оценку параметра, характеризующего форму головной части ударника. В работе [20] рассмотрена более сложная задача многоцелевой оптимизации защитной слоистой плиты, когда одновременно учитывались требования максимизации величины баллистических предельных скоростей и минимальности весовых или стоимостных характеристик используемого материала. В рамках такой постановки задачи с использованием эволюционного метода поиска глобального экстремума были найдены наилучшие слоистые структуры защитных конструкций.

В работах [21–23] впервые поставлена задача оптимального распределения механических характеристик по толщине плиты минимального погонного веса, обеспечивающей полную остановку ударника в момент его выхода из преграды. В рамках эмпирической модели (1) при помощи принципа максимума Понтрягина была получена оптимальная структура неоднородной преграды для цилиндрических, конических ударников, а также цилиндрических ударников с конической головной частью [22]. В работе [22] предполагалась линейная зависимость между динамической твердостью и плотностью материалов, что приводило к оптимальным конструкциям в виде слоистых плит. В работе [23] для цилиндрического ударника исследовался случай нелинейной связи H d ( р ) , при этом предположении получено, что оптимальные преграды могут иметь непрерывное распределение свойств по толщине. В работе [24] представлен иной подход к проблеме поиска оптимальной структуры преграды минимального погонного веса. Исследована задача проектирования слоистой плиты минимального погонного веса из заданного конечного набора материалов, обеспечивающей полную остановку цилиндрического ударника с конической головкой в момент его выхода из преграды. Решение задачи в рамках модели Сагомоняна получено при помощи метода игольчатых вариаций .

Данная статья посвящена развитию работ [21–24], в том числе, поиску оптимального решения на основе модернизированной эмпирической зависимости (1) с учетом трения и ослабляющего влияния свободных поверхностей плиты.

1. Классическая постановка и качественные результаты

Рассмотрим процесс динамического проникания жесткого осесимметричного тела в плиту при ударе по нормали и поставим следующую задачу: требуется из заданного конечного набора материалов спроектировать слоистую преграду минимального веса, которая обеспечивает остановку движущегося в ней ударника в момент выхода его носовой части на тыльную сторону плиты. Для описания процесса динамического проникания используем эмпирическую зависимость (1) для удельной силы сопротивления прониканию о (рис. 1).

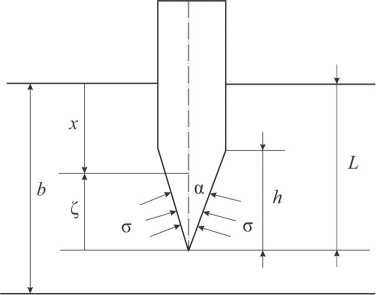
Рис. 1. Схема внедрения цилиндрического тела с конической головной частью в плиту

Рассмотрим случай динамического проникания в слоистую плиту ударника конической формы. В случае произвольного распределения плотности р и динамической твердости H d по толщине плиты силу сопротивления прониканию ударника F можно вычислить, учитывая (1), по следующей формуле [21, 22]:

L

F ( L ) = 2 п tg² a f ( L - x )[ H d ( x ) + k р ( x ) u ² ( L )] dx , 0

где L - текущая глубина внедрения ударника; x - координата, отсчитываемая от лицевой поверхности преграды; a - угол полураствора конуса; k = sin² a для конуса.

Учитывая (2) и равенство — = и, можно при помощи второго зако-dt на Ньютона Mи = -F записать уравнение движения ударника в преграде d^- = - EJ (L - x)[ Hd (x) + k p( x )u2 (L)] dx,            (3)

dL о

„ 4ntg2a где E = —m—, M - масса ударника.

Граничные условия для уравнения (3): в момент соударения с плитой скорость ударника равна и ₀, а движение ударника в преграде происходит до полной его остановки в момент выхода носовой части на тыльную сторону плиты.

U ( L = 0) = U ₀, и ( L = b ) = 0.                     (4)

Введем дополнительные фазовые координаты

У 1 =U ², У 2 = L ( L - x ) H d ( x ) dx , y 3 = J H d ( x ) dx , 0                                  0

LL y ₄ = J ( L - x ) p ( x ) dx , y ₅ = J p ( x ) dx , 00

тогда уравнение (3) с помощью новых переменных y t; г = 1,^,5 можно записать в виде системы обыкновенных дифференциальных уравнений, а полный процесс движения, учитывая (4), описывается системой y‘=-E(у2+kyi у4), у2 = у3, у3=Hd, у4=у5, у5=p,

У 1 ( 0 ) = u 0 , y , ( 0 ) = 0, i = 2, ^ ,5.                     (5)

Систему (5) можно записать в векторной форме:

У ' = f ( У , p ) , x >  0,

У 1 ( 0 ) = и 0 , У , ( 0 ) = 0, I = 2, ^ ,5.                     (6)

Соотношения (6) определяют управляемую систему, роль управления играет пара { p ( x ), b } , где p - распределение плотности по толщине плиты; b - общая толщина плиты. Управляющая функция p принадлежит классу кусочно-постоянных функций с областью значений из конечного дискретного множества.

Критерий качества управления имеет вид функционала

b

F0[p, b ] = J p( x) dx ^ min, а граничные условия представляют собой условие обращения в нуль скорости ударника в момент выхода носовой части на тыльную сторону плиты

F 1 [ p , b ] = У 1 ( b ) = 0.

Соотношения (6)–(8) определяют математическую постановку оптимизационной задачи. Отметим, что для создания оптимальной преграды имеется конечный набор материалов – это приводит к дискретной структуре области значений управляющей функции ρ. Для такого класса функций нельзя построить малые вариации управления, поэтому при решении задачи применяется метод игольчатых вариаций [25]. Этот метод заключается в построении конечных вариаций управления на множестве малой меры.

Конечная вариация управления p определяется на множестве малой меры М значением го :

Р * ⁽ x ) =

го , x еМ , 1

p, xё М, при этом возмущенное управление р* порождает вариацию функционалов (7)–(8):

5F0 = J[го-р]dx+ р(b)5b,(10)

М

• 5F1 = J V [ f (го)-f (р)] dx+dyb 5 b,

м где V - вектор сопряженных переменных, который находится из сопряженной системы уравнений

• V’ = Eky 4 V i , V 2 = E V i , V 3 = —V 2 , V 4 = Eky 1 V 1 , V 5 = —V 4 ,

V1 (b) = 1, V,(b) = 0, i = 2,^,5.(12)

Из условия (8) и первого уравнения системы (5) можно получить равенство ddb = -E[У2 (b) + kyi (b)У4 (b)] = -Ey2 (b) .

Согласно (8) на возмущенном управлении получаем 5 F 1 = 0, используя последнее равенство и соотношения (11), (13), выражаем вариацию 5 b через вариацию управления р

• 6 b =      ^V [ f И—f (р)] dx.

ЕУ 2 ( b ) м

Подставив (14) в (10), найдем

5F = J|[r( У М)—Г( y ,V,®)] dx,(15)

м где

Г ( у , V , ® ) = — ( 1 + a V 5 ) ®— a V з Н а ( ® ) +Ф ( У , V ) ,

Р(b)

a =----г—.

^Е У 2 ( ^b )

При оптимальном управлении 5 F 0 >  0, что, при учете (15), можно представить в виде принципа максимума Понтрягина

Г( у ,у,р opt) = max Г( у ,v, to), оеО где Q - заданный набор материалов.

Анализируя полученное выражение для гамильтониана Г , можно сделать ряд качественных выводов относительно оптимальной структуры преграды. Для этого рассмотрим геометрическую интерпретацию необходимых условий оптимальности.

Отложим в прямоугольной системе координат по оси абсцисс плотность р , а по оси ординат - динамическую твердость Н_а . Материалу из заданного множества Q будет соответствовать точка на плоскости. Таким образом, множеству исходных материалов соответствует совокупность точек на плоскости, выпуклая оболочка которой образует многоугольник (рис. 2). Максимум гамильтониана достигается на одной из вершин многоугольника – это означает, что в оптимальную преграду входят только материалы, лежащие на границе множества исходных материалов. Следовательно, смена материала в слоистой плите осуществляется лишь по смежным вершинам многоугольника.

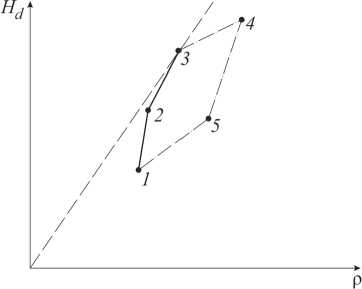
Рис. 2. Многоугольник исходных материалов

Можно сформулировать ряд свойств оптимальной структуры слоистой плиты.

Свойство 1. В допустимый набор могут входить только материалы, которым соответствуют вершины части границы многоугольника, заключенной между вершиной, соответствующей материалу с минимальной плотностью, и вершиной, через которую проходит касательная (пунктирная линия на рис. 2), проведенная через начало координат.

Свойство 2. С тыльной стороны плиты всегда расположен материал с наименьшей плотностью.

Свойство 3. В оптимальной плите материалы могут располагаться только в такой же последовательности, в которой расположены соответствующие им вершины на части границы многоугольника, соответствующей допустимому набору.

Свойство 4. Если касательная к многоугольнику проходит через точку, соответствующую материалу с минимальной плотностью, то оптимальная плита является однослойной из материала с минимальной плотностью.

Из свойств 1–4 следует, что в оптимальной конструкции плиты слои из разных материалов располагаются в порядке убывания плотности в направлении от лицевой поверхности к тыльной.

Используя свойства 1–4, можно получить качественные результаты оптимизационной задачи с несколькими материалами при динамическом проникании конуса в слоистую плиту.

В задаче с двумя материалами для конического ударника оптимальная структура полностью определяется параметром В, который зависит лишь от механических характеристик данных материалов. Ес- ли для двух материалов с параметрами р1,H 1 и р2,H2, р1 <р2 выполняется соотношение H2/ р2 < H 1/ р1, то оптимальная преграда однослойная легкая р1,H 1. В противном случае оптимальная преграда является двухслойной с лицевым твердым и тыльным легким слоем р2 ир1. Условие H2/ р2 < H 1/ р1 в эквивалентной форме имеет вид B > 0, где B = (H 1р2 - H 2р1)/(р2-р1). Условие B > 0 геометрически означает, что прямая, проходящая через точки (р1,H 1) и (р2,H2), пересекает ось Hd выше оси р . В противном случае B < 0 прямая пересечет ось Hd ниже оси р.

Обобщим результат на случай задачи о трех материалах. Требуется из заданного набора трех материалов р 1 , H ₁; р * , H * и р ₂, H ₂ сконструировать плиту минимального погонного веса, обеспечивающую полную остановку конического ударника в момент его выхода из преграды. Рассмотрим задачу в условиях кусочно-линейной связи динамической твердости H d и плотности р:

H d ( р ) = А р + B ( реQ 1 ) , H d ( р ) = D р + B i ( реQ 2 ) ,

B i = B + р * ( A - D ) , Q i = { р ( t ) : R i <р ( t ) <р * , ( t е [ 0, t , ] ) } ,       (17)

Q 2 = { р ( t ) : р * < р ( t ) < р 2 , ( t е [ 0, t k ] ) } , Q i uQ 2 = Q .

Анализируя свойства оптимальной преграды, можно получить критерии оптимальной структуры в зависимости от параметров В и В ₁.

Рассмотрим варианты оптимальной структуры плиты для различных значений параметров В и В ₁.

• А)    B >  0, В ₁ >  0. В этом случае обе прямые, проходящие через точки ( р^ H ₁ ) , ( р * , H * ) и точки ( р * , H * ) , ( р ₂, H ₂ ) , пересекают ось H d выше оси р . Это означает, что касательная к многоугольнику проходит через точку ( р ₁, H ₁ ) , и оптимальной является однослойная плита из материала р ₁, H ₁ (рис. 3, а ).

  

  а

  
  
  

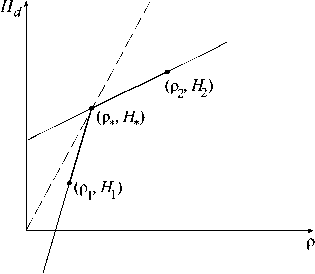
  б

  Рис. 3. Расположение материалов в случае А ( а ) и Б ( б)

  
  

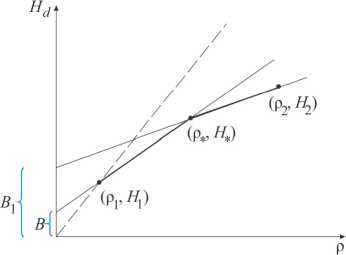
Б) B <  0, B 1 >  0 . Для этого случая получен следующий результат: прямая, проходящая через точки ( р 1 , H 1 ) , ( р * , H * ) , пересекает ось H d ниже оси р , а прямая, проходящая через точки ( р * , H * ) , ( р ₂, H ₂ ) , пересекают ось H d выше оси р . Следовательно, касательная к многоугольнику проходит через точку ( р * , H * ) , и оптимальной является двухслойная плита вида р * ир ₁ (рис. 3, б ).

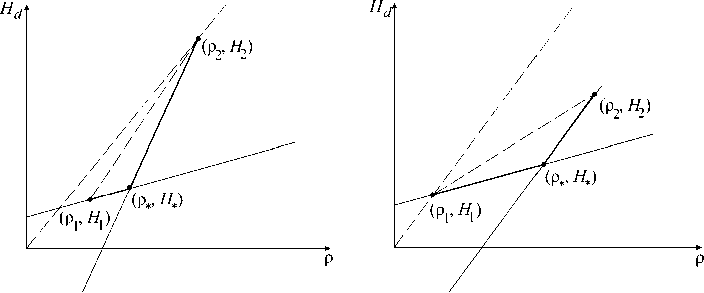
а                              б

Рис. 4. Расположение материалов в случае В: а - вариант 1; б - вариант 2

• В)    B >  0, B 1 <  0 . В этом случае прямая, проходящая через точки ( р 1 , H 1 ) , ( р * , H * ) , пересекает ось H d выше оси р, а прямая, проходящая через точки ( р * , H * ) , ( р ₂, H ₂ ) , пересекает ось H d ниже оси р. Возможны два варианта: касательная к многоугольнику проходит через точку

( р ₂, H ₂ ) , тогда оптимальная плита имеет двухслойную структуру вида р ₂ ир ₁ (рис. 4, а ); касательная к многоугольнику проходит через точку ( р ₁, H 1 ) , при этом оптимальной является однослойная преграда из материала р 1 , H ₁ (рис. 4, б ).

Граничное положение оптимальных областей соответствует следующему случаю: обе точки ( р ₁, H ₁ ) и ( р ₂, H ₂ ) лежат на касательной к многоугольнику. Отсюда следует, что если B <  X В₁ , то оптимальная преграда - двухслойная вида р ₂ up _1? иначе - однослойная р ₁, H ₁. Параметр ^Х = ^- ( р 1 / р 2 ) - ( р 2 ^-р * ) / ( р * ^-р 1 ) ■

Г) B <  0, В ₁ <  0 . Этому случаю геометрически соответствует следующая ситуация: обе прямые, проходящие через точки ( р ₁, H ₁ ) , ( р * , H * ) и точки ( р * , H * ) , ( р ₂, H ₂ ) , пересекают ось H d ниже оси р. Касательная к многоугольнику проходит через точку ( р ₂, H ₂ ) .

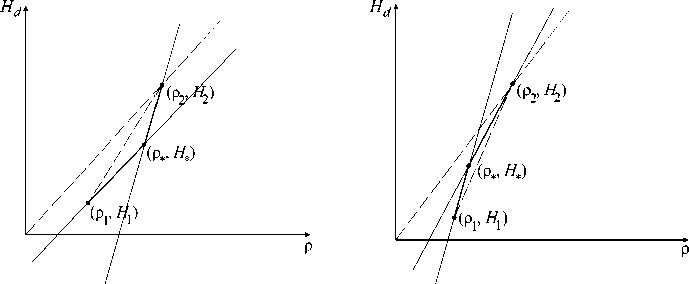
а                                   б

Рис. 5. Расположение материалов в случае Г: а - вариант 1; б - вариант 2

В рассматриваемом случае также возможны два варианта: точка ( р * , H * ) лежит ниже прямой, проходящей через точки ( р ₁, H ₁ ) и ( р ₂, H ₂ ) , при этом в оптимальную плиту входят два материала р ₂ ир ₁ (рис. 5, а ); точка ( р * , H * ) лежит выше прямой, проходящей через точки ( р ₁, H ₁ ) и ( р ₂, H ₂ ) , при этом в оптимальную плиту входят три материала р ₂ ир * ир ₁ (рис. 5, б )

Граничное положение оптимальных областей определяет условие B = B 1 . Следовательно, при условии B <  B 1 оптимальной является трехслойная плита вида p ₂ up * up , , а при условии B >  B 1 - двухслойная плита p ₂ up 1 . Основные результаты представлены на рис. 6.

Рассмотрим задачу с n материалами для конического ударника. Предположим, что проектировщик располагает набором из n материалов p 1 , H 1 ; ^ ; p _n , H_n , из которого нужно синтезировать плиту минимального погонного веса, гасящую скорость конического ударника до нуля.

Условие кусочно-линейной зависимости динамической твердости H d от плотности p примет вид

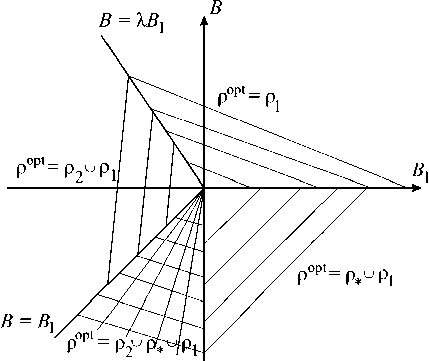
Рис. 6. Оптимальные области параметров В и В 1

H d ( p ) = A i p + ^B1 ( p^e « 1 );.■■; H d ( p ) = A n p + B ( p^e« n ) , « 1 = { p ( t ) : p i ^p ( t ) ^p 2 , ( t e [ 0, t k ] ) } ;...;

« n - 1 = { p ( t ) ^: p n - 1 ^p ( t ) ^p n , ( t ^e [ ⁰, t k ] ) } ,

B i = ( Hp_M - H + 1 p . )/( p i + 1 - p i ), « 1 u ^ uQ n - 1 =« .

Сформулированные выше свойства позволяют отобрать материалы, которые входят в оптимальную плиту. Таким образом, можно получить качественное решение динамической оптимизационной задачи для общего случая - задачи с n материалами.

Рассмотрим варианты оптимальной структуры плиты в зависимости от параметров B i ; i = 1, . , n .

А) B 1 < 0, . ,B_n - 1 < 0; B 1 <...< B_n - 1 . Только в этом случае возможен n -слойный вариант структуры в качестве оптимальной. Касательная к многоугольнику проходит через точку ( р n , H_n ) , а точки исходного множества ( р 1 , H 1 ) , . , ( р _n,H_n ) лежат на выпуклой вверх части границы многоугольника. В случае нарушения одного из условий случая А из оптимального набора исключаются определенные материалы.

Б) B i >  0 или B i >  B i _{+ 1}. В этом случае ( i +1)-й материал исключается из оптимального набора, и задача сводится к задаче с ( n –1) материалами. Геометрическая интерпретация случая Б соответствует следующей картине: точка ( р i _{+ 1}, H i _{+ 1} ) лежит ниже выпуклой вверх оболочки точечного множества. Так как точки, которым соответствуют материалы из оптимального набора, лежат на границе многоугольника, то материал р i _{+ 1}, H i _{+ 1} не войдет в оптимальную структуру плиты.

Суммируя вышесказанное, можно построить алгоритм определения оптимальной структуры плиты для задачи с n материалами. Вычисляем значения параметров B 1 , . , B_n 1 , последовательно проверяя условия А. Если условия А верны, то в оптимальную структуру входит n материалов. В противном случае при выполнении условия Б из оптимального набора исключается ( i +1)-й материал, ( i +2)-й материал становится ( i +1)-м, вычисляется новое значение параметра B_i , и данная процедура повторяется снова. В итоге останется некоторое количество материалов, которые войдут в оптимальную плиту, либо задача сведется к разобранной выше задаче о трех материалах.

2.    Влияние трения и свободных поверхностей плиты

Исследуем процесс ударного внедрения конического тела в слоистую преграду при учете дополнительных факторов – влияния краевых эффектов свободных поверхностей и трения на сопротивление прониканию.

Приведем постановку задачи оптимизации в более общем виде. С помощью введения коэффициента k _oc эмпирическая зависимость (1) записывается в виде

O = k oc H d ⁺ k P^U 2 ,

где k _oc – коэффициент ослабления.

Основываясь на экспериментальном факте [1, 26], что значение динамической твердости (имеющей смысл удельной работы вытеснения материала преграды) вблизи свободных поверхностей будет существенно отличаться от значения, которое она принимает в глубинных слоях, можно определить коэффициент k _oc следующим образом:

0 r 0

—L + kr. ,

, 1- k ^k oc =—Г" l ₀

0 ,

koc = 1, k0

^k oc = —.

l

-

^- L + 1 -

l 0

1 0 < L < b - 1 0 ,

, b - 1 0 <  L <  b ,

где b – конечная глубина внедрения; l ₀ , k_r ⁰ – параметры ослабления (рис. 7). Отметим, что соотношения (20) верны при условии 2 1 0 <  L_k . Случай 2 1 ₀ >  L_k соответствует тонким преградам.

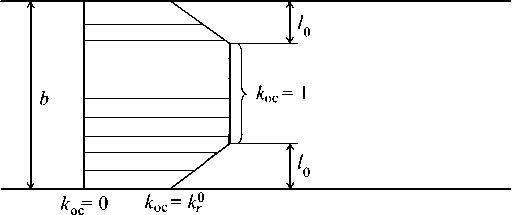
Рис. 7. Зависимость коэффициента ослабления от глубины внедрения

Учет трения приводит к появлению дополнительного слагаемого в соотношении (2):

L

F ⁽ L ) = 2 ⁿ tg² a f ⁽ L ^- x ^)[ k oc ( x ) H d ⁽ x ) +

L

+k p( x) и2 (L)] dx+2n tga f (L - x )т( x) dx, где т - удельная сила трения.

Уравнение движения ударника в преграде примет вид

d ( u ²)         L, .              .         . _ . L .

-----= -EJ(L - x)[k (x)H (x) + kp(x)u2 (L)]dx - DJ(L -x)т(x)dx, dL 00

_ 4ntg2a      4ntga где E=—M—, D=—M—, M - масса ударника.

Уравнение (22) с помощью новых переменных запишем в системы обыкновенных дифференциальных уравнений:

y‘=-E(y2+kyy4)-Dy6, y2 = yз,y3=kocHd, y4=y5, y5 =p, y‘= y7, y7 = т, y 1 (0) = u0, y,(0) = 0, i = 2,^,7.

Сопряженная система уравнений имеет вид

V 1 = Eky 4 V 1 , V 2 = E V i , v 3 = -V 2 , v' 4 = Eky 1 ^ 1 , V 5 = -V 4 ,

V 6 = D V i , V‘ 7 =-V 6 , V i ( b ) = 1, V i ( b ) = 0, , = 2, ^ ,7.

Гамильтониан системы (23) запишется в виде

Г ( y , v , w ) = - ( 1 + a V 5 ) ®- a V з k_o=Hd ( ® ) - a V 7 т ( ю ) +Ф ( y , v ) ,

виде

a =

p( b)

Ey 2 ( b ) ⁺ Dy 6 ( b )

Анализируя коэффициенты при to , H_d и т в выражении (25), можно сформулировать свойства оптимальной плиты. Рассмотрим по отдельности каждый из случаев – учет трения и учет краевых эффектов свободных поверхностей.

При учете трения гамильтониан (25) принимает вид

Г ( y , v , to ) = - ( 1 + a V 5 ) to- a V 3 H d ( to ) - a V 7 T ( to ) +Ф ( y , v ) .

Функции V3, V5 и V7 являются отрицательными и монотонно возрастающими. Следовательно, коэффициенты при Hd и т положительны и монотонно убывают, коэффициент при to убывает, достигая на правом конце значения –1. Это означает, в предположении, что материал с большим значением Hd имеет и большее значение т, что в оптимальной плите материалы могут располагаться лишь по мере убы- вания плотности в направлении от лицевой поверхности к тыльной, причем в окрестности тыльной поверхности располагается материал с минимальной плотностью. Таким образом, учет трения для конуса не приводит к качественно новым результатам по сравнению с базовой постановкой задачи.

При учете фактора влияния свободных поверхностей преграды на сопротивление прониканию гамильтониан приводится к следующему виду:

r ( y лмо ) - ( 1 + a v 5 ) ю^- a V 3 k oc H d И^+ф ( y , v ) .

Коэффициенты при H _d и to ведут себя подобно разобранным выше случаям на промежутке [ l 0 , L k ] , следовательно, с тыльной стороны плиты на толщине [ l 0 , L_k ] справедлив тот же качественный результат – материалы располагаются в порядке убывания. Так как функция a V 3 отрицательна и монотонно возрастает, а k oc положительна и монотонно возрастает, то учет эффекта ослабления приводит к тому, что с лицевой стороны поверхности оптимальной преграды (в области [ 0, l 0 ] ) материалы могут расположиться в порядке возрастания - это качественно новый результат.

Рассмотрим динамическое внедрение в слоистую преграду цилиндрического ударника с конической головной частью высотой h . Приведем постановку задачи в общем виде: удельная сила сопротивления вычисляется по уточненной эмпирической зависимости (19), в соотношении для силы сопротивления учтено трение. Соотношение для силы сопротивления прониканию ударника F разбивается на две части:

L

2 п tg² a J ( L - x )[ k oc ( x ) H d ( x ) + k p ( x ) u ² ( L )] dx +

L

+ 2 n tg a J ( L - x ) t ( x ) dx , L <  h ,

F ( L ) = ^

L

2 n tg 2 a J ( L - x )[ k oc ( x ) H_d ( x ) + k p ( x ) u ²( L )] dx +

L - h

L

+ 2 n tg a J ( L - x ) t ( x ) dx , L >  h .

L - h

Уравнение движения ударника при этом будет иметь вид

d ( и ²) = <  dL

L

E J ( L - x )[ k _oc ( x ) H_d ( x ) + k p ( x ) u ² ( L )] dx -

L

D J ( L - x ) t ( x ) dx , L <  h ,

L

E J ( L - x )[ k _oc ( x ) H_d ( x ) + k p ( x ) u ²( L )] dx -

L - h

L

D J ( L - x ) t ( x ) dx , L >  h .

L - h

При помощи введения новых переменных уравнение (27) запишется в виде системы уравнений

У ’ = - E ( У 2 + кУ 1 У 4 ) - Dy 6 , У 2 = У з - hk oc ( x - h ) H ( x - h ) ,

У 3 = ^k oc ( ^x ) H d ( ^x ) ^{- k} oc ( ^{x - h} ) H d ( ^{x - h} ) , У 4 = У 5 ^- h p ( ^{x - h} ) ,

У ³=p ( x ) -p ( x - h ) , y ‘= y 7 - h t ( x - h ) , y 7 = т ( x ) -т ( x - h ) ,

У 1 ( 0 ) = u 0 , y , ( 0 ) = 0, i = 2, ^ ,7.

Для данной системы введем следующие обозначения: y = { у₄ } ; f = { f } - вектор, составленный из первых слагаемых правых частей системы; g = { g i. } - вектор, составленный из вторых слагаемых правых частей системы. Эту систему с помощью единичной функции

1, x >  0,

I ( ^x ) =‘

запишем в векторной форме:

0, x <  0

У ‘ = f ( У , p ) - g ( x - h ) I ( x - h ) , x > 0,

У ! ( 0 ) = u 0 , y , ( 0 ) = 0, i = 2, ^ ,7.                    (28)

Вектор сопряженных переменных находится из системы

¥‘ = - f> , V t ( b ) = 1, V i ( b ) = 0, i = 2, ^ ,7.            (29)

Функция Гамильтона примет различный вид на отрезках [ 0, L - h ] и [ L - h , L ] :

Г ( y , V , w ) =-to- a { [v ₃ ( x ) - h v ₂ ( x + h ) — V ₃ ( x + h ) ] k _oc H d ( w ) + + [v 5 ( x ) — h V 4 ( x + h )— V 5 ( x + h ) ] w+

+[v 7 ( x ) — h V 6 ( x + h ) —V 7 ( x + h ) ] t ( w ) } , [ 0, L — h ] ,

Г(y,v, w) = —w—a[vз (x) • kocHd (w)+V5 (x) " w+V7 (x)" T(w)], [L—h,L], где a p(b)

Ey 2 ( ^b ) ⁺ Dy 6 ( ^b )

3.    Численный пример

Конкретные толщины слоев оптимальной плиты определяются численно. Численный алгоритм решения оптимизационной задачи аналогичен [22]. Выбирается некоторое допустимое управление p ( x ) и малый параметр A x , моделирующий множество малой меры. Вводится равномерная сетка x , = 0, x j = x j _{— 1} + A x , j = 1, S ( x_{S — 1} <  b <  x_S ) . В точках x j + A x /2 вычисляются значения y и V , они предполагаются постоянными для всего отрезка [ x j , x j _{+ 1} ] . Затем интегрируется система уравнений (28), находятся в узлах сетки значения y ( x ) и b . В полученной точке x = b задаются граничные условия для сопряженных функций и интегрируется система (29). На отрезке [ x j , x j _{+ 1} ] находится новое значение p j из условия максимума:

Г( yj,Vj,Pj) = max Г( yj,Vj,p), если pj =p(xj + Ax /2), то осуществляется переход к отрезку [xj+1,xj+2] и определяется новое значение pj+1; если pj ^p(xj +Ax/2), то выбирается новое управление

*

p = 1

pj, xe [xj,xj+1 ], p( x), x ё [ xj, xj+1 ], затем выполняется переход к первому этапу, и вновь интегрируется исходная система уравнений (28) при x = xj+1.

Управление улучшается до правого конца интервала x = b ; процесс завершается, когда р ( x ) не меняется ни при каких j .

В качестве примера было рассмотрено динамическое проникание жесткого цилиндрического ударника с конической головной частью высотой 1,6 - 10² м при угле полураствора конуса 15° и начальной скоростью 500 м/с. В таблице представлены механические характеристики исходных материалов.

Механические свойства материалов

Номер материала	H d , кгс/см2	ρ, г/см3	Номер материала	H d , кгс/см2	ρ, г/см3
1	1500	2,8	4	6500	4,59
2	2500	2,8	5	12500	7,95
3	4500	4,59	6	13200	7,95

В результате расчетов получено, что оптимальной является трехслойная плита, сконструированная из 6-го, 4-го и 2-го материалов. Их относительная толщина в процентном соотношении составляет 70,5 : 2,33 : 27,17.

Численные расчеты подтвердили, что учет краевого эффекта ослабления может привести к качественно новому результату. При данных к ^ = 0,5 и 1 ₀ = 1,5 и двух исходных материалах H ₂ = 13200 кг/см², р ₂ = 7,95 г/см³, H 1 = 4500 кг/см², р 1 = 2,8 г/см³ в задаче об ударе цилиндрического ударника с конической головкой оптимальной является трехслойная преграда вида р 1 ир ₂ ир 1 . Относительная толщина (%) составляет соответственно 16,85 : 54,2 : 28,95. В задаче о трех материалах при исходных данных к Г = 0,1, l ₀ = 1,0, H ₃ = 13200 кг/см², р ₃ = 7,95 г/см 3 , H ₂ = 6500 кг/см², р ₂ = 4,59 г/см³, H 1 = 2500 кг/см², р 1 = 2,8 г/см 3 оптимальная плита синтезируется из пяти слоев р 1 ир ₂ ир ₃ ир ₂ ир 1 при процентном соотношении их относительной толщины 5,7 : 0,62 : 65,67 : 0,44 : 27,57.