Оптимизация параметров тестового воздействия для повышения чувствительности методов вибродиагностики силы сухого трения при вынужденных колебаниях динамических систем

связи определение динамических, т.е. постоянно изменяющихся во времени и функций других величин параметров сухого трения, является сложной, но актуальной задачей.

Эффективность диагностических процедур нелинейной вибродиагностики может быть значительно повышена путем оптимизации тестового воздействия для достижения наилучшей чувствительности. Использование теории чувствительности для анализа и синтеза сложных механических систем детально рассмотрено в [2], где также представлен подробный аналитический обзор отечественных и зарубежных публикаций по данной теме.

При решении задачи диагностировании функция чувствительности диагностического признака П к изменению контролируемого параметра q (например, коэффициента жесткости или диссипации) определяется выражением

Δ ПП Δ qq

где А П - абсолютное изменение диагностического признака П , соответствующее абсолютному изменению контролируемого параметра q на величину А q .

Из анализа выражения (1) следует, что, если относительное изменение отклика (диагностического признака П) численно равно относительному изменению контролируемого параметра q, то чувствительность диагностического метода равна единице (µ=1). При разработке диагностических процедур или при оптимизации тестовых воздействий следует стремиться к достижению максимально возможных значений функции чувствительности. Это позволит получать более достоверные и качественные результаты вибрационного контроля даже при использовании достаточно «грубой» и более дешевой контрольноизмерительной аппаратуры. Использование функции чувствительности (1) вследствие ее безразмерности позволяет сравнивать различные диагностические методы и алгоритмы между собой и выявлять наиболее предпочтительные диагностические признаки по критерию максимальной чувствительности к возникающему дефекту.

Для возможности исследования поведения функции чувствительности при изменении параметров тестового воздействия (например, амплитуды и частоты гармонической вынуждающей силы) или собственных параметров диагностируемого объекта вместо выражения (1) возможно использовать выражение частной производной функциональной зависимости информативного признака П по контролируемому параметру q i :

дП(q1, q2, q3,..., qj, P-, to,...)

.  (2)

В качестве примера рассмотрим возможность выбора оптимизированного тестового воздействия для повышения чувствительности диагностического метода, заключающегося в идентификации силы сухого кулонова трения в упруго-диссипативной колебательной системе с одной степенью свободы на основе определения «правых» асимптот фазо-частотных характеристик. В основе метода лежит нелинейный эффект наличия «правых» асимптот ФЧХ (рис. 1) вынужденных колебаний системы с сухим трением и линейно-вязким сопротивлением [1], принятый в качестве диагностического признака. Аналитическое выражение для «правых» асимптот ФЧХ можно получить, находя значения следующего предела [3]:

Ф = Нт Ф = - arcsin ф/ ^да

p

— ^jm

Р  од/_>оо

Po Р р

¹Ф р ) ' to/ ^p

,  (3)

где F - модуль силы сухого кулонова трения; P о - амплитуда вынуждающей гармонической силы; ш - частота вынуждающего гармонического воздействия; p - собственная частота колебательной системы.

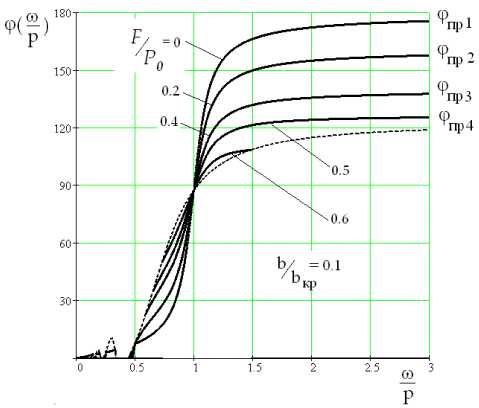
Рис. 1. Семейство ФЧХ безостановочных режимов движения системы с сухим кулоновым и вязким трением

Тогда

п * F              п * F

Ф„„ = 180 - arcsin----= 90 + arccos---- пр

² * P o                 ² * P o (4)

. F/ .< I ¹

при ограничении на значение / P - J i + ^ y ^)2 для обеспечения безостановочных режимов движения. Таким образом, функция Ф пр = f ( Fp ) (рис. 2) представляет собой фрагмент арккоси-нусоиды.

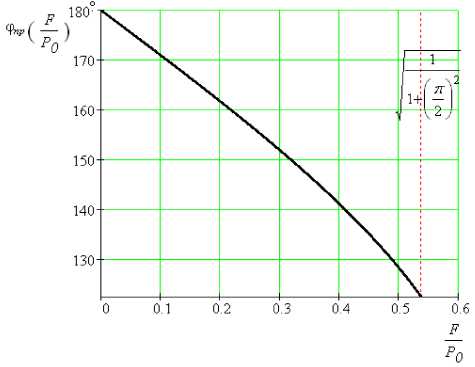
Рис. 2. Зависимость значений «правых» асимптот ФЧХ от относительной силы сухого трения F / P ₀

Следовательно, определив асимптоты

ФЧХ при го/p>>1, представляется возможным количественно оценить силу сухого трения к 2 * P

F =     - * ^sin Ф пр

П ,

2       о или в безразмерной форме Fp^ - — * sin Фпр при ограничении на значение

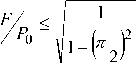
« 0,537

Ввиду нелинейности функциональной зависимости (5) функция чувствительности

~ ₌ ^д Ф пр ₌        1

^d F   1 1 - ( n F / 2 P o ) 2

рассматриваемого спо-

соба идентификации также имеет нелинейный характер, что видно из анализа ее графика (рис. 3).

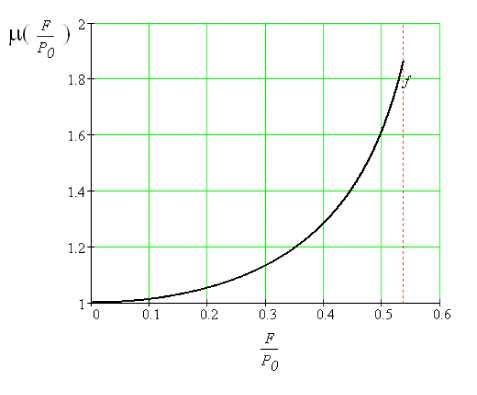
Рис. 3. График зависимости безразмерной функции чувствительности µ от относительной силы сухого трения F/P 0

Из анализа рис. 3 следует, что за счет соответствующего выбора амплитуды P 0 гармонической вынуждающей силы тестового воздействия, а именно такой, чтобы отношение

F / P 0 стремилось «слева» к значению J_{1 +} (п/ ) 2 , чувствительность рассматриваемого идентификационного метода может быть существенно увеличена.

Выводы: определив и реализовав оптимальные значения тестового воздействия, в данном случае, соответствующую амплитуду вынуждающей гармонической силы Р 0 , представляется возможным значительно повысить чувствительность диагностической процедуры нелинейной вибродиагностики контроля уровня диссипативных параметров сухого трения в механической системе. Такая возможность увеличения чувствительности при реализации методов нелинейной вибродиагностики является их ощутимым преимуществом по сравнению с линейными подходами.