Оптимизация поворотного маневра и синтез законов гиросилового наведения космических аппаратов и свободнолетающих роботов

Проблемы синтеза оптимального [1] программного углового движения механической конструкции космического аппарата (КА) при его пространственном поворотном маневре (ПМ) наиболее актуальны для решения задач оптико-электронного наблюдения заданных участков поверхности Земли и пространственной транспортировки грузов космическими роботизированными модулями (КРМ). В предыдущих работах автора [2,3] представлены некоторые результаты аналитического синтеза программы ПМ КА на заданном интервале времени t е T p = [ t 0 , t f ], t f = t 0 + T _p с краевыми условиями общего вида и аналитического расчета [3] соответствующего программного управления силовым гироскопическим комплексом (СГК) минимально избыточной структуры. Полученные при этом программы ПМ КА не являются единственными, поэтому возникают задачи расчета как строго оптимальной программы пространственного ПМ, представляющей ее предельные свойства по функционалу “управлений” из пространства Соболева W₂³[ t ₀ ^p , t _f ^p ] [4], так и приближенно оптимальной программы ПМ, которая рассчитывается по явным аналитическим соотношениям. Статья содержит решение этих задач, результаты сопоставления полученных программ ПМ КА, а также результаты аналитического синтеза законов гиросилового наведения КА с помощью СГК кратной схемы на основе шести гиродинов (ГД) [5].

Задача оптимизацииповоротного маневра

Задача оптимизации ПМ КА на заданном интервале времени T_p состоит в определении кватерниона ориентации Л ( t ) связанного с корпусом КА базиса B = { b i } относительно известного инерциального базиса I , векторов угловой скорости to ( t )и ускорения g ( t ) для кинематических соотношений

Л ( t ) = 2 Л ( t ) ® to ( t );

to ( t ) = g ( t );                    ⁽¹⁾

g ( t ) = v = g * ( t ) + to ( t ) x g ( t );

из условия минимизации интегрального квадратичного критерия tfp                                      tfp

I o = 1 f < v ( t ) , v ( t ) >  d т = 1 f v² ( t ) d т ^ min (2) pp 00

при заданных краевых условиях для кватерниона Л = ( X ₀, X ), X = { X i }, векторов to = { ro i } и g = { g i } = to на левом ( t = 1 0 ) и правом ( t = t f ) концах ПМ:

Л ( 1 0 0 ) = Л o ; to ( 1 0 0 ) = to o ; g ( 1 0 0 ) = g o ; (3) Л ( t f ) = Л f ; to ( t f ) = to f ; ^{g (} t f ) = ^g f . (4) Здесь вектор v = g ( t ) считается “управлением” и физически представляет собой абсолютную производную вектора ускорения g ( t ) базиса B относительно базиса I .

Определение углового положения КА в инерциальном базисе I с помощью кватерниона Л(t) весьма рационально, но не является единственным. При применении углов Эйлера-Крылова в последовательности 31'2'' (первый элементарный поворот на угол 0, второй поворот на угол у и, наконец, третий поворот на угол v) исходные прямые и обратные кинематические соотношения с использованием составленного из указанных углов вектора-столбца ф = {0, у, и} имеют вид ф = D(ф)to; го = С(ф)ф. (5)

Здесь матрицы

С ( Ф ) =

C v

5 V

- ⁵ V C Y

⁵ Y ^C V ^C Y

DW = .’

CY

C v C Y 5 v 5 Y

-

5 v

^{0    5} V C Y

Y    ^vUY

0     C v

где введены обозначения C _a = cos а и 5 _a = sin a .

Отметим, что задача оптимизации функционала (2) топологически эквивалентна

что оптимальное “управление” имеет вид v( t ) = p ( t ). Решение сопряженной системы (10) получается в явном виде как v ( ‘ ) = c _ф ; ^{ц (} ‘ ) = ^c ю - ^c ф ⁽ ‘ ^- ‘ 0 p ) ^; Р ( ‘ ) = c s ^- c o ( ‘ ^- ‘ 0 p ) ⁺ c ф ( ‘ ^- ‘ 0 p )² / ² , где постоянные c _ф , c _ю и c ₈ следует определить по заданным краевым условиям (8) и (9).

Структура оптимального “управления” v( t ) = p ( t ) известна, поэтому решение исходной системы (7) также представляется в явном аналитическом виде

s ( t ) = 8 0 + c . ( t - 1 0 ) - c ^{ю (} t ^- * « ⁾²

+ cф (t - tp )3 6;

ю ( t ) = ю° +8° ( t - 1 0 ) + c ^{8 (} t ^- t p ⁾²

- c„ (t - tp )3 + cф (t - tp )4

6           24

задаче оптимизации pp

₁ t_{f                         1} t_f

I 1 = ... /1 ^{v ( T )|} d ^т=₇- J v ^{( t )} d ^T ^ min (6)

Tp t0p                Tp t0p наиболее важного для практики функционала I1 , имеющего ясный физический смысл – среднее значение модуля ускорения КА (либо КРМ) относительно инерциального базиса I в процессе его поворотного маневра.

Оптимальное одноосное движение

Такая задача конечно является элементарной: на заданном интервале времени t e T p = [ t 0 , t f ], t f = t 0 + T p для системы

ф = ю; О = s; 8 = v (7)

с заданными краевыми условиями

Ф ( t p ) = ф ⁰; ю ( t _o p ) = ю ⁰; 8 ( t _o p ) = s ⁰, (8)

ф ⁽ ‘ f ) = Ф ^f ; ^{ю (} ‘ f ) = ^{ю f} ; ^{s (} ‘ f ) = ^{8 f} (9) необходимо найти скалярное “управление” v( t ) в задаче оптимизации (2). Вводится функция Гамильтона H = - v² /2 + uo + Ц8 + p v и система дифференциальных уравнений для сопряженных переменных

V = -5H / 5ф = 0 ;

ц = -dH / am = -v; (10) p = -dH / 5s = -ц.

Из условия оптимальности c H/ d v =- v + p = 0 принципа максимума Понтрягина следует,

ф ( t ) = ф ⁰ +ю ⁰( t - 1 0 ) + ⁸ 0 ⁽ t 2 ‘ 00 ) 2

+ c , ( t - t p ) 3 - c „ ( t - ‘ 0 )⁴ + c ф ( t - t p ) 5 . 6         24        120

Наконец, три постоянные c _ф , c _ю и c ₈ определяются в явном виде при подстановке ф ( t f ), ю ( t f ) и s ( t f ) решения (11) в заданные краевые условия (9).

Таким образом, оптимальное по критерию (2) движение КА относительно произвольной k-ой оси представляется функцией ф _k( t ) в классе полиномов (сплайнов) пятой степени нормированного времени т = ( t - 1 0 )/ T p с [0,1] с аналитическими зависимостями

Фк ( ^{т )} = ⁸ к ^{( т )} = ⁸ k

+ т (6 a ₃ + 12 a ₄ т + 20 a ₅ т ²)/ T p ²;

^ф к ^{( т )} = ^ю к ^{( т )} = ^ю к ⁺⁸ k T p ^т

+ т ²(3 a ₃ + 4 a ₄ т + 5 a ₅ т ²)/ T p ; (12)

ф к ^{( т )} = ф к ^{+ T} ( ° k T p ⁺ ^ k T^ ^/2

+ т2( a 3 + a 4т + a 5т2)), где юк,sk, к = 1,2,3 - начальные скорость и ускорение в элементарном повороте, а коэффициенты ai, i = 3 ^ 5 определяются в явном виде по векторно-матричному соотношению a3

a ₄

a ₅

= A

f 0   0     02

Ф к - Ф к - ^ю k T p - ^£ k T p /2 T p « -ю k -s k T p ) tX -s k )

с матрицей

10    - 4 1/2

A = - 15  7    - 1

6    - 3 1/2

Приближенно оптимальное пространственное движение

Приближенное оптимальное решение пространственной задачи основывается на необходимом и достаточном условии разрешимости классической задачи Дарбу – определения Л ( t ) в аналитическом виде (в том числе в квадратурах) из уравнения Л ( t ) = 1 Л ( t ) ® to ( t ) при известных Л ₀ и to ( t ).

Введем базис E0 , фиксированный в инерциальном базисе I кватернионом Л0 (1), и подвижные базисы Ek (k = 1,...n), где базис En совпадает со связанным базисом B . Необходимое и достаточное условия разрешимости задачи Дарбу состоят в возможности представления вектора угловой скорости to (t) в виде to (t) = to n( t) + to n.1( t) + • • • +to 1( t), где вектор to k(t) имеет неизменное направление в базисе Ek-1 и является вектором угловой скорости базиса Ek относительно базиса Eк-1, т.е. в виде to (t) = to n-1( t)+~„( t )®(tont( t) + л n ,< t )®(ton-3( t) n            n           n-1           n-1           n-2

+ Л n-2(t)®( + to0(t)) • ®Л n-2(t) )®Л n-1(t) )®Л n(t), где вектор-столбец to k-1(t), k = 1,...n составлен из проекций вектора to k(t) фиксированного направления в базисе Ek-1, а Л k(t) является кватернионом ориентации базиса Ek относительно базиса Ek-1.

Решение поставленной задачи представляется как результат сложения трех одновременно происходящих элементарных поворотов “вложенных” базисов E _k вокруг ортов e _k осей Эйлера, положение которых определяется из краевых условий (3), (4) исходной пространственной задачи. Кватернион Л ( t ) ориентации КА в базисе I определяется произведением

Л ( t ) = Л ₀ ® Л 1 ( t ) ® Л ₂( t ) ® Л ₃( t ).   (14)

Здесь для k = 1,2,3 кватернион ^Л k ⁽ t ) = (^cos( Ф k ( t ^)/2), e k sin Ф k ⁽ t )^/2)),     ^где

Ф _k( t ) и e _k - текущий угол и орт оси Эйлера k-го поворота. В силу неподвижности орта e _k в базисе E _{k - 1} имеем to _k( t ) = ф _k( t ) e _k, e k ( t ) = Ф k ( t ) e k ^и e k ( t ) = p; ( t ) e k . Обозначения краевых условий всех 3 элементарных поворотов относительно ортов e _k приведены в табл. 1.

Пусть кватернион Л * = ( Х * ₀ , X * ) = Л ₀ ® Л f имеет орт оси Эйлера e ₃ = X * /sin( р * /2) третьего поворота, где угол р * = 2arccos( X 0 ) вычисляется по значениям кватернионов Л ₀ и Л f . Для первого и второго элементарных поворотов принимаются начальные и конечные значения кватернионов в виде

Л 1 ( t p ) = Л 1 ( t f ) = Л 2 ( 1 0- ) = Л 2 ( t f ) = 1 , (15) а краевые условия по кватерниону для третьего элементарного поворота – в виде (мат ф)

Л 3 ( t o ) = 1.   _г

Л ₃( t f ) = (cos( p; f /2), e ₃ sin( рз /2)), где p f = р * , 1 - единичный кватернион, чт о соответствует значениям углов p 0 =p 2 = 0, p 0 =р 2 = 0 и фЗ = 0 , представленным в табл.. Орт e ₁ оси Эйлера первого поворота назначается из условия его ортогональнос-

Таблица. Краевые условия

k Тип элементарного движения Краевые условия на левом конце траектории (t = t0p) Краевые условия на правом конце траектории (t = tf) Ф ю £ Ф ю £ 1 Движение по орту e1 Ф0 ю0 S0 Ф f ю[ £f 2 Движение по орту e2 ф 2 ю 2 £ 2 ф 2 ю 2 £ 2 3 Движение по орту e3 ф 3 ю 3 £ 3 ф 3 ю 3 £ 3 ти к орту e3 по следующему простому алгоритму:

ef ^ to 0/w 0; ef = to f/to f;

e O = £ o / s 0 ; e f = ^£ f ^{/ s} f ;

• 1)    a = : e f - <  e f , e ₃ >  e ₃ и если a = | a | > 0, то e 1 = a / a ;

• 2)    иначе

a = : e f -< e f , e ₃ >  e ₃ и если | a | > 0, то e 1 = a / a ;

• 3)    иначе

a =: eO -< e0, e3 > e3 и если | a |> 0, то e1 = a / a; (16) 4) иначе a =: e£f -< e£f, e3 >• e3 и если | a |> 0, то e1 = a / a;

• 5) иначе

третий поворот относительно орта оси Эйлера e ₃ является единственным, т.е. кватернионы Л 1 ( t ) = Л 2 ( t ) = 1 .

Наконец, орт e ₂ оси Эйлера второго поворота определяется по стандартной формуле e ₂ = e ₃ x e 1 из условия аналитического построения правого ортонормированного базиса на совокупности ортов e ₁ , e ₂ и e ₃ .

Все векторы to k(t) = pk(t)ek, £k(t) = pk(t)ek и £k(t) =Pk(t)ek в каждом элементарном повороте представляются в аналитическом виде при явном задании функций времени pk(t) (12), оптимальных по критерию (2) для элементарных вращений. Вектор угловой скорости to (t), векторы углового ускорения £(t) (и при необходимости его производной £(t) - “управления” v(t) в (1)) при начальных обозначениях векторов to (1)(t) = to 1(t), £ (1)(t) = £ 1(t), £ (1)(t) = £ 1(t) определяются аналитически по рекуррентному алгоритму: для верхних индексов k = 2,3 последовательно вычисляются to k (t) =: Лк( t )®to (k-1)( t )®Л k( t);

to ^(k)( t ) = to k ( t ) + to k ( t );

• £ k ( t ) = : Л _к( t ) ® £ ^(k-1)( t ) ® Л k ( t );

£ ^(k)( t ) = £ k ( t ) + £ k ( t ) + to k ( t ) x to k ( t ); (17)

£ k ( t ) = : ~ k ( t ) ® £ ^(k-1)( t ) ® Л k ( t );

£ ^(k)( t ) = £ k ( t ) + £ k ( t ) + (2 £ k ( t )

+ to k (t) x to k(t)) x to k(t) + to k (t) x £k(t) , в итоге искомые векторы получаются как to (t) = to(3) (t) , £ (t) = £(3) (t) и £ (t) = v (t) = £ (3) (t) .

Функции переходов р _k( t ) по углам поворота в элементарных движениях относительно ортов e _k,k = 1,2,3 должныудовлетво-рять краевым условиям (см. табл. 1):

по угловым скоростям р k=< to0, ek >,    k = 1,2,3;

p^ f =< to f , e 3 > , _f                     ~         (18)

p ik =< Л*®(tof - e3p 3)®Л*,ek > k = 1,2;

по угловым ускорениям p0=< £0,61 >-p2p3;

^p 2 =< ^£ 0 , e 2 >  ^+p 1 ^p 3 ^;

p 3 =< £ 0 , ^e 3 > ^- P 1 P 2 ^;

£ mm = Л *® £f ® v~ *;(19)

f m       ff pi =< £ f, e1 >-P2 pf;

p 2=< £^m, e2 >+pifpf; f m       ff p3 =< £f, e3 >-p1p2

Краевые условия (18) и (19 получаются на основе рекуррентного алгоритма (17) с учетом условий (15) для значений кватернионов первого и второго поворотов на правом и левом краях поворотного маневра.

Элементарные повороты конечно можно выполнять и при совмещении ортов Эйлера ek с ортами bk базиса B . При этом функции переходов p k(t) по углам поворота в элементарных движениях соответствуют углам Эйлера-Крылова в выбранной последовательности и краевые условия должны вычисляться с использованием нелинейных кинематических соотношений (5). Рассмотрим практический пример ПМ, соответствующий пространственному угловому переходу к цели наблюдения на противоположенной стороне полосы обзора за время Tp = 76 с. Пусть заданы краевые условия ф0 = {-35.4,37.28,39.09}°;

ф f = {20,56.92,-30} ° ;

to ₀ = {0.05,0.485, -0.125} ° / c ;

to f = {0.286, -0.265, -0.142} ° / c ;

• 8    0 = {0.002459,0.000575, - 0.000240} ° / c 2

• 8    f = {-0.003241, - 0.002348,0.000320} ° / c и пространственный поворотный маневр выполняется по оптимальному закону для каждого элементарного поворота в двух вариантах:

• a )    для указанных углов Эйлера-Крылова относительно ортов b _k базиса B ;

• b )    для последовательности поворотов относительно выбранных ортов Эйлера e _k .

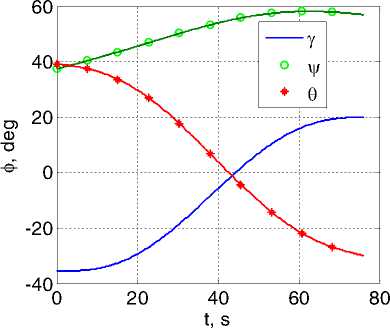
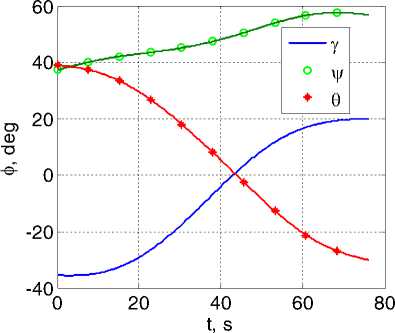
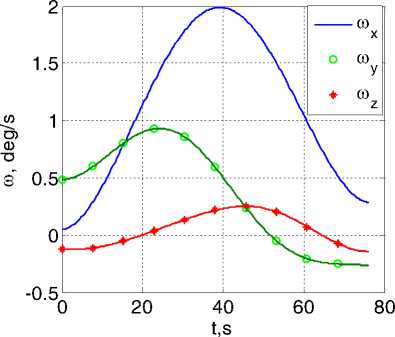
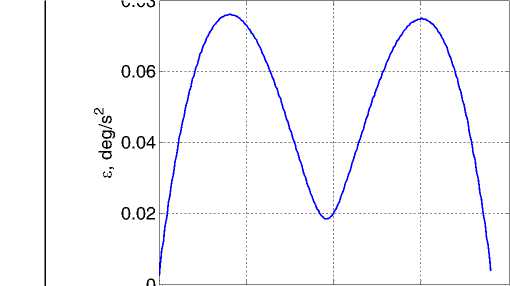
Полученные численные результаты представлены на рис. 1 и рис. 2. Функционал I1 (6) принимает значения I1 = 0.057рад/c2 в варианте a) и I1 = 0.051рад/c2 в варианте b) , т.е. по функционалу I1 вариант b) имеет “выигрыш” в 11%. По исходному функционалу I0 (2) такой “выигрыш” составляет 22%. Рис. 2 ясно иллюстрирует преимущества варианта b) также в отношении максимального уровня модуля ускорения. На основании многочисленных расчетов с самыми разнообразными краевыми условиями установлено, что вариант b) формирования приближенно оптимального ПМ всегда имеет выигрыш по сравнению с вариантом a) – до 40% по фун-

U)

15) о

"О

-0.

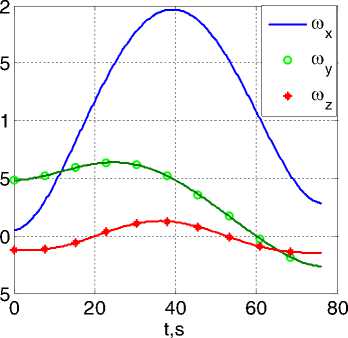
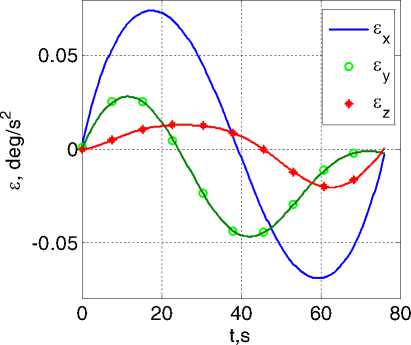
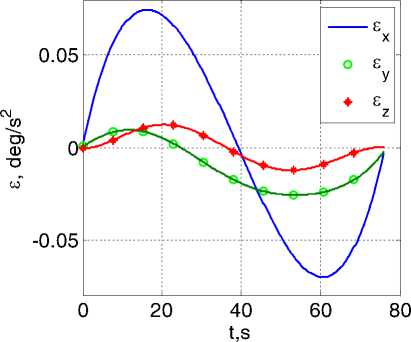
Рис. 1. Изменение кинематических параметров при поворотном маневре: вариант a ) слева

г8/6эр ‘з

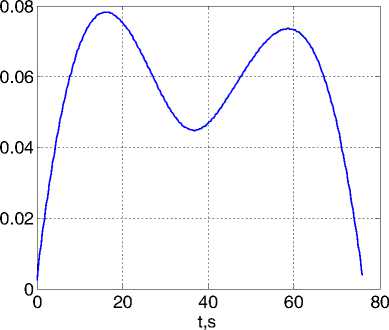
0.08

40 t,s

Рис. 2. Изменение модуля ускорения при поворотном маневре: вариант a) слева кционалу I1 для ПМ при больших углах.

Оптимальный поворотный маневр

Для исходной нелинейной задачи (1) –

• (4) составляется функция Гамильтона

H = —1 < v, v >+ 1 < Т, Л® to >

+ < Ц, 8 > + < p, V >, а для сопряженных переменных (кватерниона т и векторов Ц,P) — сопряженная система дифференциальных уравнений

Т =—дH / дЛ = 1Т® to ;

Ц = —дH / dto = -1Л ®Т = -1Л ®сф®Л;

p = —дH / д8 = —Ц, где постоянный [1] вектор сф = {cфк} в дальнейшем должен определяться. Условие оптимальности дH / dv = —v + p = 0 в соответ- ствии с принципом максимума приводит к оптимальному управлению v(t) = p(t). Структура решения необходимых далее компонентов сопряженной системы (20) такова:

Ц ⁽ t ) = c _m

t

— ¹ J Л ( т ) ® С ф ® Л ( т ) d т ;

t

^p 0

p ⁽ t ) = ^{v (} t ) = c _e ^— c _m ⁽ t ^— t o’ )

+1J J (Л(s)®сф®Л(s)ds) dт, t0pt0p где векторы cm = {cmk} и cE = {cek} подлежат определению. Это позволяет представить структуру решения всех компонентов исход- ной прямой системы (1) также в аналитическом виде, где постоянные векторы сф, cm и сЕ должны быть выбраны на основе численных методов с удовлетворением краевых условий (3) и (4). Несложно убедиться, что в этой структуре при движении КА относительно только одной оси имеется полное совпадение оптимального управления с представленными выше результатами (10), (11).

Для численного построения строго оптимального по критерию (2) управления для нелинейной задачи (1) – (4) применяется стандартный итерационный метод Ньютона. При этом в качестве решения “стартовой” задачи принимается аналитическое приближенно оптимальное движение, составленное из трех одновременно выполняемых элементарных вращений относительно специально выбранных трех ортов Эйлера e _k . В такой “стартовой” задаче постоянные векторы ^с ф = ^{ c ф к ^}, c _m = ^{ c _m k ^} и c _e= ^{ c J имеют компоненты, аналитически полученные для оптимального движения в каждом элементарном повороте. Уточнение значений этих постоянных векторов выполняется итерационно, с использованием совместного численного интегрирования прямой и сопряженной систем дифференциальных уравнений, линеаризованных в окрестности решения на предыдущей итерации.

Установлено, что таком выборе начальной точки (“стартовой” задачи) итерационного процесса по методу Ньютона имеется быстрая сходимость – обычно необходимо 23 итерации для получения численного решения с приемлемой точностью. Различие меж- ду приближенно оптимальным управлением (аналитическим решением “стартовой” задачи) и строго оптимальным управлением весьма незначительное – до 3% по функционалу I1 для практически важных поворотных маневров КА и КРМ с произвольными краевыми условиями (3) и (4).