Оптимизация прессового инструмента при производстве низкотемпературных сверхпроводников

В работе предложена методика определения оптимальных углов технологического инструмента при прессовании моно-, би- и триме-таллических заготовок. В основу оптимизации положено минимальное напряжение прессования, обеспечивающее минимальные энергозатраты. Задача совершенствования и оптимизации технологии производства низкотемпературных композиционных сверхпроводников для достижения необходимых производственных объемов выпуска при соответствии требованиям качества является актуальной. Важным является разработка теоретических основ и методик проектирования технологических процессов применительно к технологии производства низкотемпературных композиционных сверхпроводников, научно обосновывающих выбор технологических режимов и технологической оснастки для повышения качества низкотемпературных композиционных сверхпроводников и обеспечения высоких технико-экономических показателей их производства [9].

При обработке металлов давлением широкое применение находит процесс прессования. Сущность прессования заключается в выдавливании материала, помещенного в замкнутый объем, через канал, образованный прессовым инструментом [1, 6]. Достоинством прессования является благоприятная схема напряженного состояния с преобладающим влиянием сжимающих напряжений, обеспечивающих повышенную пластичность прессуемого материала. Поэтому прессование широко используется при обработке давлением малопластичных трудно-деформируемых металлов и сплавов [2].

Одним из основных параметров прессования является усилие прессования. При этом необходимо иметь минимальное усилие прессования с целью снижения энергозатрат. Полное усилие при прессовании представляется в виде суммы составляющих [1, 7]:

P = T + Т + Т + Т + Т ± Q,                (1)

кр м пл к ш ,                               V 7

где Ткр - результирующая сила трения на поверхности контейнера; Тм -результирующая сила трения в зоне деформации на поверхности контакта прессовой матрицы и заготовки; Тпл - усилие, затраченное на пластическую деформацию; Тк - результирующая сила трения на поверхности калибрующего пояска матрицы; Тш - усилие, затрачиваемое на преодоление сил трения между металлом и пресс-шайбой; Q - усилие противодавления или переднего натяжения (±Q).

Полное усилие прессования (1) приводится к среднему напряжению прессования,

% = P / F o ,                         (2)

где F _o - площадь сечения исходной заготовки.

Соответствующие отдельные составляющие уравнения (1) приводятся к удельным нормальным и касательным напряжениям системы внешних сил (рис. 1).

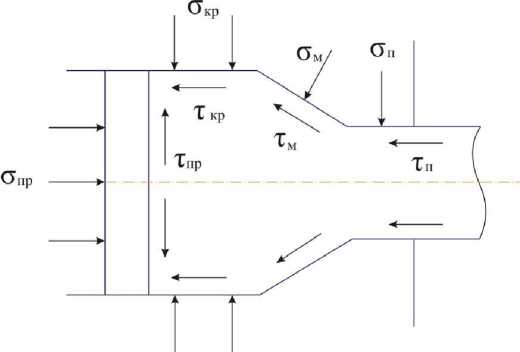
Рис. 1. Схема сил, действующих при прессовании

Из практики прессования известно наличие оптимальных углов наклона образующей конической матрицы к оси прессования ам. От угла ам в соотношении (1) зависят составляющие Тпл и Тм, поэтому оптимизация геометрии прессовой матрицы заключается в определении оптимального значения угла ам . В работе излагается методика определения оптимального значения угла ам из условия обеспечения минимального значения усилия прессования изделий круглого сечения.

Напряжение прессования при пластическом деформировании [1]

£

° пл = J° , ^d£ ,                               ⁽³⁾

где о _s - сопротивление деформации прессуемого материала; £ - степень деформации при прессовании.

В работах [3, 4] степень деформации определена с учетом вытяжки и дополнительных деформаций сдвига на входе в конический технологический инструмент и выходе из него в следующем виде:

еср =ln X+тд^ШОм, где X = R021R12 - коэффициент вытяжки; R0 и R 1 - радиусы исходной заготовки и пресс-изделия соответственно.

Для усредненного значения сопротивления деформации составляющая напряжения прессования, связанная с пластической деформацией, с учетом соотношения (4), может быть определена следующим образом:

°пл = ° s I ^lnX + :Лг^^ам I -

В свою очередь проекция результирующей сил трения на ось прессования для конической поверхности рабочей части матрицы выглядит так:

Тм = Fm • f • °, • cosа_м, м м J s        м ⁷

где f - коэффициент трения в зоне деформации; т_м - касательное напряжение; F - поверхность конической части матрицы.

Из геометрических соотношений для боковой поверхности конуса имеем о лR12 ( s = . 1 ■

sin а,

■ м V R

1 -

С учетом соотношения (7) проекция результирующей силы трения на ось прессования будет выглядеть следующим образом:

T = ° s • ^л R ^{2 (X - 1)} f ^ctS^a M ,

В общее среднее напряжение прессования вклад от преодоления сил трения в зоне деформации можно определить как

° м = ° s (^X - 1) f C^M I X .

Оптимальный угол наклона образующей матрицы к оси прессования определяется из условия минимума полного напряжения прессования:

^ ( о 5 tga_M

+ о ) = 0.

M

После дифференцирования соотношений (5) и (9), преобразований и упрощений получим tg^ =1,14

/f (X - 1)

N X

и соответственно а™т м

= arctg 1,14 V

f (X - 1) "

X )

.

На рис. 2 приведены расчетные значения оптимальных углов матриц при прессовании в зависимости от вытяжки для различных значений коэффициента трения. Из рис. 2 следует, что с увеличением X и уменьшением f оптимальные углы матриц возрастают.

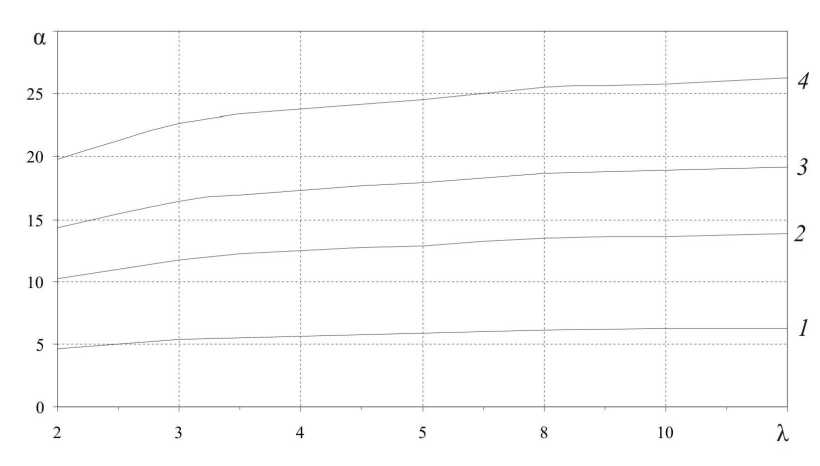
Рис. 2. Расчетные значения оптимальных углов при прессовании в зависимости от вытяжки для различных значений коэффициента трения: 1 - f = 0,01; 2 - f = 0,05; 3 - f = 0,1; 4 - f = 0,2

Рассмотрим деформацию прессованием биметаллической сверхпроводниковой сборной заготовки, состоящей из сердечника (Nb-Ti или Nb) и медной оболочки (рис. 3). Полагаем, что при прессовании составной заготовки коэффициент вытяжки одинаков и для сердечника, и для оболочки.

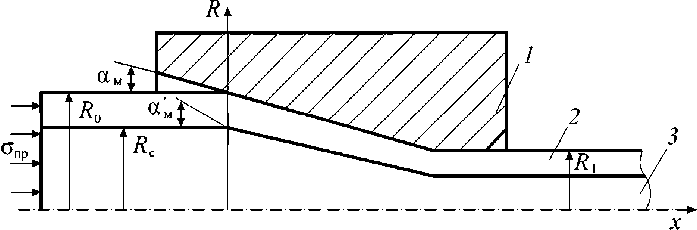
Рис. 3. Схема прессования биметаллической сборной заготовки: 1 - пресс-форма; 2 - оболочка; 3 - сердечник

Для центральной части (сердечника) степень деформации [2]

£_с = lnX 4

4 tg<,

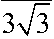
где а М - угол наклона образующей сердечника к оси прессования; X -вытяжка.

Из геометрических соотношений рис. 3 следует

R tgам = -tgам,                           (14)

где R _с - радиус сердечника; R 0 - наружный радиус заготовки.

С учетом уравнения (14) средняя степень деформации сердечника описывается следующим образом:

£ = lnX + —tga_M. ^с 3^ R ₀ ^{6 м}

Для усредненного значения сопротивления деформации сердечника составляющая напряжения, связанная с его пластической деформацией, с учетом соотношения (15), может быть определена следующим образом:

R ^

о ^с = о ^с lnX 4—4=— tga .                 (16)

“ ⁵ (     3Д R 0 g ^м J

Напряжению (16) соответствует доля полного усилия прессования центральной части (сердечника) биметаллической заготовки [3]:

P c = ” R X

lnX + 4 R c

(     3-J3 R о

^

^tg^a м

)

Аналогичный расчет выполнен для наружной части (оболочки) биметаллической заготовки.

Напряжение прессования оболочки для усредненного значения сопротивления деформации

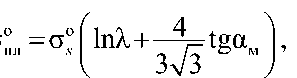
° o ( ^{lnX +} 34з^“ м

где о О - усредненное значение сопротивления деформации материала оболочки.

Соответственно, доля общего усилия прессования, затраченного на деформацию,

P c = я ( R ² - R c )

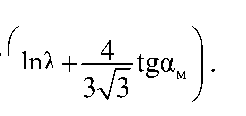
_v      3V3      у

Для оболочки необходим учет сил трения в рабочей части зоны деформации. Проекция результирующей сил трения на ось прессования запишется в виде формулы

Т м = о О я К> - 1) f йд« м ,

где R 1 - радиус наружной поверхности биметаллической заготовки на выходе.

Вклад от преодоления сил трения в зоне деформации в общее среднее напряжение прессования можно определить следующим образом:

° м = ^{о О (Х - 1)} f *ё^а м ^/Х •

Оптимальный угол наклона образующей матрицы к оси прессования определен из условия минимума полного напряжения прессования, и а_м зависит лишь от о п _р, ° п _р, ° м , поэтому

—; К + о ^, + о м ) = ^0.

При этом суммарное напряжение прессования, включающее лишь величины, зависящие от ам

R 2 (

° = ° c    ^Ы+

4 R c

3 3 R 0

Л

R=)

^tg^a м ⁺ ° " ¹   „2

V R У

У

х

(.

х lnX +—4

V 3

) tg«M + °.

У

o R 1²

^s R 0²

Выражение (23) после преобразований можно представить в виде

° z

= ° ^R c² ln^X +A R c tg« M + ° о ( i - 1 ) f -1

V     3^3       У V Xyv tga,

+ lnX+

43tg« M У , (24)

где X = R 0² / R 1² - вытяжка; R _c = R _c / R 0 .

После дифференцирования уравнения (24) по tgaM, преобразований и упрощений получим аМпт = arctg

₁₉₇ 1     -^f (^X - 1) -

’ \/X ( 1 - R _c ² + ° s /° o^o R c³ )

На рис. 4 представлены результаты расчетов по формуле (25) при коэффициенте трения f = 0,1 и отношении ° c /о ^ = 3,33. Данное отношение сопротивлений деформации сердечника и оболочки соответствует горячему прессованию биметаллической сверхпроводящей заготовки, состоящей из ниобиевого сердечника и медной оболочки, для температуры 600 °C. При этой температуре для Nb ° c = 30 МПа, для меди ° 0 = 9 МПа [5].

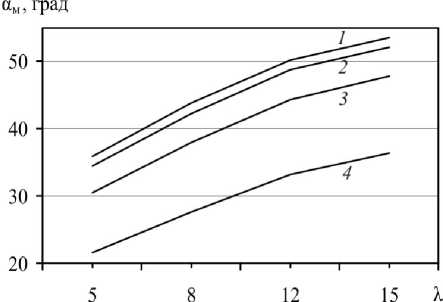
Рис. 4. Зависимость оптимального угла конусности от коэффициента вытяжки при прессовании биметаллической заготовки для коэффициента трения f = 0,1 и при отношении ° ; /о ^ = 3,33 ; 1 - R_с = 0,25; 2 - 0,45; 3 - 0,65; 4 - 1

Как следует из рис. 4, при прессовании биметаллической заготовки размер угла конусности зависит не только от вытяжки, но и от соотношений геометрических размеров заготовки и условий трения.

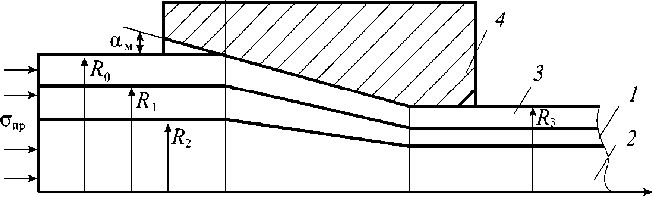
На рис. 5 рассмотрена деформация прессованием триметалличе-ской сверхпроводниковой сборной заготовки [8, 10], состоящей из сердечника (медь) радиусом R 2 ; промежуточного слоя из сверхпроводникового материала (Nb-Ti или Nb) радиусом R 1 и медной оболочки радиусом R о .

х

Рис. 5. Схема прессования триметаллической сборной заготовки: 1 - промежуточный слой из сверхпроводникового материала (Nb-Ti или Nb); 2 - сердечник из меди; 3 -оболочка; 4 - прессовый инструмент

Аналогично расчетам для биметаллической заготовки выполним расчеты, полагая, что при прессовании составной заготовки коэффициент вытяжки одинаков и для сердечника, и для оболочки. Для сердечника из меди (см. рис. 5) степень деформации [1]

^е ср ⁼ ln ^{Х +} A?tg< ’

где «м - угол наклона образующей сердечника к оси прессования. Из геометрических соотношений следует tgаM ^ тг^ам, R0

где R 2 - радиус сердечника из меди; R ₀ - наружный радиус заготовки.

Для промежуточного слоя из сверхпроводникового материала степень деформации

^Е ср = ln X ⁺ Аг^ .

где а м - угол наклона образующей сердечника к оси прессования.

Из геометрических соотношений следует

R

tg«M = ^1tgaM , где R1 - радиус промежуточного слоя; R0 - наружный радиус заготовки. Тогда средняя степень деформации сердечника из меди [4]

R

р ⁼ ln^{X +} 373 - ^tg“ M •

Для промежуточного слоя

R р=lnX+373 - *д“м •

Для оболочки еср=ln X+3 4л^ •

Для усредненного значения сопротивления деформации сердечника составляющая напряжения, связанная с пластической деформацией сердечника, с учетом соотношений (31) и (32), может быть определена следующим образом:

с    „с О — О л пл      5 2	( ln X + V	4 R 2 3 3 R 0	tg^	^ 7	•                       (33)
°L = О 5 1	( ln X + V	4 R 1 3 3 R 0	Шам	7	.                       (34)

Напряжению (33) и (34) соответствует доля полного усилия прессования центральной части сердечника триметаллической заготовки:

р =F

1 c 1 2

° $2

( л R      ^

ln ^{X +} 343" R O     I

+ F 1

О " 1

I ^lnX+37

( R ^ — tg«,

V R0 7

м

Л

,(35)

)_

где F 1 и F ₂ - соответствующие площади.

Аналогичный расчет выполнен для наружной части (оболочки) триметаллической заготовки.

Напряжение прессования оболочки для усредненного значения сопротивления деформации

< = ° o о ( in ^X + 343^

где о О0 - усредненное значение сопротивления деформации материала оболочки.

Соответственно доля общего усилия прессования, пошедшего на деформацию, может быть определена следующим образом:

(.                   Л

^Pc = ^Я • ( ^-О - [ ^- 2 ^{+ -} 1 ] ) • ° . 0 ^ In^{X +} ^^

Для оболочки необходим учет сил трения в рабочей части зоны деформации. Проекция результирующей сил трения на ось прессования запишется в виде

Т м = ° о • я • ^(X - 1) f ctga м ,

где R з - радиус наружной поверхности триметаллической заготовки.

В общее среднее напряжение прессования вклад от преодоления сил трения в зоне деформации составил

° м = ° Оo (X - 1) f ctg^ / X .                     (39)

Оптимальный угол наклона образующей матрицы к оси прессования определен из условия минимума полного напряжения прессования, при этом от угла а_м зависят лишь о ^л , о^, ° м , поэтому условие минимума усилия прессования получено в виде

—(о ^с + о ^о + о ^о ) = 0.                   (40)

\Х пл пл м/                                  V /

5 ( tg^ )

При этом суммарное напряжение прессования, включающее лишь величины, зависящие от ам,

— 2 (

° ° 2    ln ^{X +}

4 ^R 2

3 3 R 0

Л tg^ ⁺ ° 7

п 2 (

■ c     in X+ s1    2

—4=—tga + з73 - о   ^м )

( — 2 — 2 Л(                Л — 2

⁺ ° oо I ^- Ч ^- тт ^{lnX +} T^т^tg^a м ⁺ ° oo-ZT ( ^{X - 1 )} f ^С^« м .

у ^- о ^- о )V 3V³     7      ^- о

Выражение (41) после преобразований представлено в виде

О

Г.

= ^О s2 R 2 ln^X + V

^3 ^R 2 ' ^tgtt M

+ О 1 R ln X ■

V

343 R •    J+

+ ° o 0 ( ^{1 -}[ R² + ^R 12 ] ) ^{ln X} +           ^{+ О} o0 X ( ^X ' • ^{f Ctga} M ’

R2              R R где X = —0- - вытяжка; R = —; R. =—

R 3^{2                 1} R 0    ² R 0

При производстве триметаллических сверхпроводников сердечник и оболочка изготавливаются из меди, а промежуточный слой (см. рис. 5) из сверхпроводника (Nb-Ti или Nb).

После дифференцирования выражения (42) по tga_M, учитывая, что a S ₂ = о О 0 , преобразований и упрощений получим

<^т = arctg

1,97

г

a

f (X - 1)

c

X     R ³ - ( R - R 2 + R - 1 )

V ° s 0                         J

.

На рис. 6 представлены результаты расчетов по формуле (43) при коэффициенте трения f = 0,1 и отношении a C/°0 = 3,33. Данное отношение сопротивлений деформации сердечника и оболочки соответствует горячему прессованию биметаллической сверхпроводящей заготовки, состоящей из ниобиевого сердечника и медной оболочки, для температуры 600 °C [5].

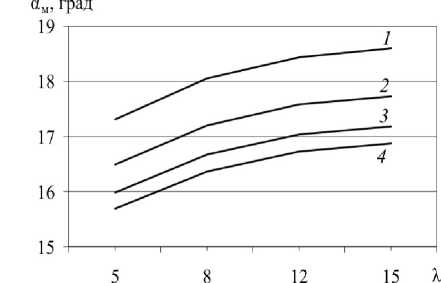
Рис. 6. Зависимость оптимального угла конусности от коэффициента вытяжки при прессовании триметаллической заготовки для коэффициента трения f = 0,1 и при отношении o S /п ^ = 3,33 ; 1 - R 1 = 1; R 2 = 0, 75; 2 - R 1 = 0,75; R 2 = 0,5;

3 – R ₁ = 0,55; R ₂ = 0,3; 4 – R ₁= 0,5; R ₂= 0,25

Таким образом, из условий минимума усилия прессования определены оптимальные углы матриц для прессования моно-, би- и триме-таллической заготовки. При этом учитываются составляющие усилия прессования, содержащие угол конусности технологического инструмента. Выявлены технологические параметры, влияющие на усилие прессования. Показано влияние вытяжки и коэффициента трения на значения оптимальных углов. Применение матриц с оптимальным углом конусности позволяет снизить энергоемкость процесса прессования при производстве низкотемпературных сверхпроводниковых изделий.