Оптимизация процесса прямого прессования проволоки из сплава ПОИН-52 методом обобщенного приведенного градиента

Прямое прессование – процесс обработки металлов давлением, который широко используется при изготовлении изделий из металлов как с низкими, так и высокими пластическими свойствами. Благодаря осуществлению трехосного сжатия, повышающего пластичность металла и позволяющего значительно деформировать его при прессовании, достигаются коэффициенты вытяжки до 1000. Прессование широко применяется при производстве изделий из алюминиевых, медных, магниевых, титановых, цинковых и других сплавов, а также стали.

В работах [1, 2] нами показано, что процесс прямого холодного прессования является весьма эффективным при производстве проволочного припоя из сплава ПОИн-52, который относится к низкотемпературным бес-свинцовым припоям. Предложенная технология производства пруткового и проволочного припоя различного типоразмера показала на практике [3] свою высокую рентабельность и конкурентоспособность при мелкосерийном производстве, однако остается открытым вопрос об оптимальности применяемых технологических параметров процесса прессования.

Основными параметрами при прессовании, которые определяют его эффективность, являются усилие прессования и скорость истечения. При этом логично, что усилие прессования как показатель энергоэффективности процесса должно быть минимальным, а скорость истечения, которая определяет производительность – максимальным.

Оптимизации процессов обработки металлов давлением посвящено большое количество работ [3–7], связано это с необходимостью повышать конкурентоспособность металлопродукции, которая определяется качеством продукции при минимизации ресурсов на ее обеспечение. Процесс прессования в данном случае не является исключением, и вопросам его оптимизации посвящены такие работы, как [8–11].

Целью настоящей работы является оптимизация процесса прямого прессования проволоки и прутков различного типоразмера из легкоплавких материалов.

В работе [12] нами разработана математическая модель прямого прессования припоя из легкоплавких материалов, позволяющая определять энергосиловые режимы прессования проволоки и прутков различного диаметра. В модели энергозатраты на процесс прессования (при пренебрежении силами трения скольжения на контактной поверхности пресс-штемпеля и контейнера) предлагается оценивать в виде суммы сил

Г = Г деф +Г_Т р , (1) где Г_де ф - усилие, осуществляющее формоизменение (пластическую деформацию); F_Tp -усилия, преодолевающие силы трения скольжения на контактной поверхности обрабатываемого металла с контейнером и с матрицей.

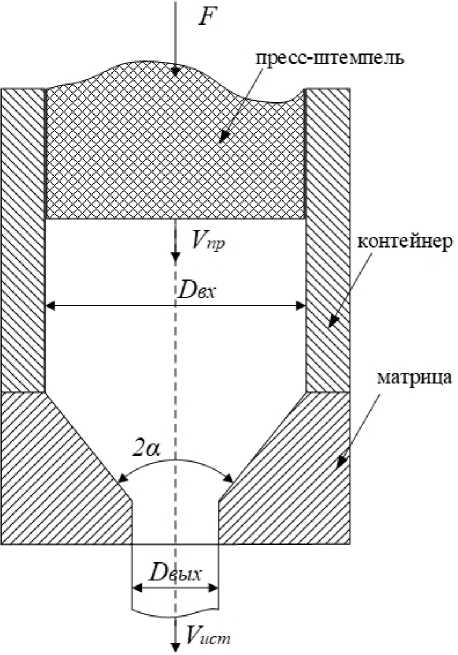
Рис. 1. Схема очага деформации при прессовании: О _вх = О _кон - диаметр заготовки на входе в матрицу равный диаметру контейнера; О _вых - диаметр проволоки (прутка) на выходе из матрицы; α – полуугол матрицы (волоки); Г _пр - скорость прессования (скорость перемещения пресс-штемпеля); У _ист -скорость истечения (скорость выхода металла из матрицы)

Факторами, влияющими на процесс прессования проволоки или прутка заданного размера, являются диаметр заготовки, полуугол матрицы, длина заготовки, скорость прессования (рис. 1). Варьируя этими факторами, можно снизить или увеличить скорость истечения и энергосиловые параметры процесса прессования. Эффективность процесса прессования определяется именно через эти два показателя, т. е. скорость истечения определяет производительность процесса, и она должна стремиться к максимуму, а энергозатраты на объем произведенной продукции должны быть минимальными.

Диаметр готовой продукции в нашем случае колеблется от 2,0 до 15,0 мм, и его определяет заказчик, следовательно, его в процессе оптимизации принимаем за постоянную величину, а вот диаметр заготовки остается на усмотрение производителя продукции, и его мы можем выбирать с целью получения оптимальных условий процесса прессования. Нужно отметить, что диаметр заготовки все же имеет ограничения по максимальному значению и связано это с технологическими ограничениями: стабильность процесса, мощность используемого гидравлического пресса, прочностные свойства применяемой оснасти. Из этих соображений ограничим максимальный диаметр заготовки для исследуемого процесса величиной 50 мм, а длину – величиной 150 мм. Для теоретических оптимизационных расчетов полуугол матрицы рассмотрим в диапазоне 2…75°, скорость прессования от 1 до 6 мм/с, а коэффициент трения будем варьировать в пределах 0,3…0,6.

Составим математическую модель задачи оптимизации процесса прямого прессования проволоки и прутков из легкоплавкого сплава ПОИн-52.

Анализ математической модели показал, что задачу следует отнести к классу задач нелинейного программирования. Поэтому в качестве инструмента для оптимизационных расчетов выберем метод обобщенного приведенного градиента (ОПГ), который часто используется на практике и широко распространен во многих программных пакетах [13–15]. В частности, будем использовать надстройку «Поиск решения» из группы команд анализа данных MS Excel [16].

Метод обобщенного приведенного градиента представляет обобщенную версию метода приведенного градиента и тоже базируется на сокращении размерности оптимизационной задачи за счет представления зависимых

переменных через множество независимых

путем применения приведенного градиента для определения направления поиска оптимума и в качестве целевой функции. Данный

подход используется для задач выпуклого про-

граммирования, но в случае с ОПГ оптимум функции f ( x ) ищется при нелинейных ограничениях h i ( x ), i = 1, m, L j <  X j <  Uj, j = 1,n, где x i и x j – элементы подмножества базисных ( x_B = { x i }, i E Г) и небазисных ( x_N = { X j }, j £ Г) переменных, соответственно. При этом I = {1, 2, …, m }, а J = { m +1, m +2, …, n }.

Тогда, с учетом обозначений

Мх)

h=I :   l;

L h_m(x)\

dH

Эхв

- dh t (x) •

;

dh _m (x)

;i E Г;

dx i

dH

Эхв

- dh t (x) ■ dh _m (x)

;jEl;

тор H ( x ) = ( H i ( x ), H ₂( x )), х E X - набор оценок решения х E X по двум критериям. В нашем случае степень предпочтительности решения х E X возрастает с уменьшением первой и увеличением второй компонент вектора H , т. е. чем меньше значение H ₁( x ) и больше значение H 2 ( x ), тем лучше решение x по двум критериям. Решение х * E X называется парето-оптимальным (оптимальным по Парето, эффективным), если не существует другого решения х E X , для которого

H 1 ( x ) ≤ H 1 ( x ^* ); (8)

H 2 ( x ) ≥ H 2 ( x ^* ). (9)

Если множество возможных оценок H ( x ) представить некоторой областью ОАВ на координатной плоскости ( H 1 , H 2 ) (рис. 2), то эффективной границей этого множества с недо-менирующими оценками будет кривая ОА.

_ dxj _

n           Гd/(x)     d/(x)     d/(x)

(х) =      .....ad = 1-dxrJ,1E Г;(5)

d/(x)     d/(x)     d/(x)

^Hf(x) =[d;—.....-^-J = hx-pE71 (6)

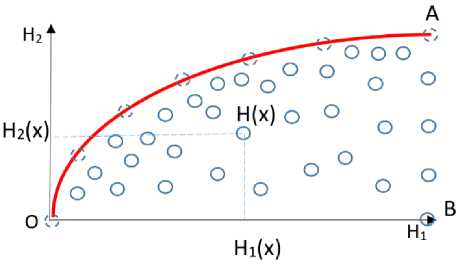
Рис. 2. Гипотетическое множество возможных оценок H ( x ), представленное областью ОАВ на координатной плоскости критерия H 1 и H 2

ОПГ вычисляется по выражению rT = d/(x) = dx^

= ^_Nf(x)^T - 4_Bf(x)^T [^ H ] "¹ dH . .     (7)

dx B    dx ^

Итак, определим целевую функцию и назначим ограничения оптимизационной задачи. В случае многокритериального поиска необходимо сформулировать понятие эффективного или оптимального решения по Парето.

Исходя из условий рассматриваемая задача двухкритериальная, так как эффектив-

ность процесса прессования оценивается усилием, которое стремится к минимуму, и скоростью истечения, которая должна быть максимальной.

Через X обозначим множество допустимых решений в нашей задаче, х E X - допустимое решение. Каждое решение х E X оценивается по двум критериям. Через H i ( x ), х E X обозначим вещественную функцию, значениями которой являются оценки решения х E X по критерию i , i = 1,2 . Тогда век-

Применительно к процедуре «Поиск решения» целевая функция должна быть одна, поэтому преобразуем нашу задачу. Вместо двух будем улучшать один критерий – отношение скорости истечения заготовки к усилию прессования. Естественно, критерии будем использовать в нормализованном (безразмерном) виде.

Исходя их практики производства данной проволоки, в качестве норм возьмём максимальную скорость истечения проволоки V ист^max = 2000 мм/с и максимальное усилие прессования F ^max = 280 000 Н. После деления фактических значений критериев на их максимальные получим нормализованные V ист^* и F ^* , т. е. значения будут находиться в интервале [0; 1].

Представим разработанную нами ранее [1, 12] математическую модель в виде электронной таблицы и определим ограничения. Из четырнадцати параметров восемь будут

зафиксированы (табл. 1). Варьироваться будут только шесть:

диаметр готовой проволоки D_BSX = 2…15 мм ( Х 1 );

длина заготовки L = 80…150 мм ( Х 2 );

диаметр контейнера D кон = 20…50 мм ( Х 3 );

скорость прессования V пр = 1…6 мм/с ( Х 4 );

полуугол матрицы (волоки) α = 2…75° ( Х 5 );

коэффициент f = 0,3…0,6 ( Х 6 ).

Из всех расчетных параметров нас будут интересовать только два – V ист ( Y 1 ) и F ( Y 2 ) (табл. 2), которые в оптимизационной задаче будут представлены одним безразмерным отношением V ист^* / F ^* ( Y 1^* / Y 2^* ) с пятью предельными вариантами (табл. 3):

V ист^max = 2000 мм/с;

V ист^max = 1500 мм/с;

V ист^max = 1000 мм/с;

V ист^max = 500 мм/с;

V ист^max = 1,8 мм/с.

В качестве граничных условий зададим требование, чтобы все параметры модели имели неотрицательные значения.

После настройки и запуска процедуры «Поиск решения» получим пять вариантов расчетов, соответствующих предельным скоростям истечения проволоки (рис. 3). По данным табл. 3 (см. рис. 3) видно, что от первого варианта к пятому значение отношений критериев оптимизации увеличивается. Наибольшее отношение Y 1^* / Y 2^* = 3,545 достига-

Таблица 1

Параметр	Размерность	Величина	Диапазон значений	Фактор
Диаметр заготовки (прутка), D вх	мм	43,64	const	-
Диаметр готовой проволоки, D вsх	мм	2,5	2…15	X1
Длина заготовки, L	мм	80	80…150	X2
Длина распресованной заготовки, L	мм	73,1	const	-
Диаметр контейнера, D кон	мм	45,64	20…50	X3
Скорость прессования, V пр	мм/с	6	1…6	X4
Сопротивление деформации заготовки, σ	МПа	10,5	const	-
Сопротивление деформации в зоне калибр. пояска, σ кп	МПа	9,5	const	-
Теплоемкость, c	Дж/(кг·К)	230	const	-
Плотность, ρ	кг/м3	7 300	const	-
Теплопроводность	Вт/ммК	86	const	-
Полуугол волоки, α	°	75	2…75	X5
Коэффициент, f	-	0,3	0,3…0,6	X6
Длина калибрующего пояска, L кп	мм	5	const	-

Таблица 2

Параметр	Размерность	Величина	Функция отклика
Коэффициент вытяжки, μ	-	333,3
Сопротивление деформации	МПа	9,99
Скорость истечения, V ист	мм/с	2000,0	Y 1
Параметр формы по Бэкофену	-	0,8
Сила деформации, F деф	Н	80 649
Сила трения, F тр	Н	35 665
в контейнере F тр I	Н	33 021
в матрице F тр II	Н	2 532
в калибр. пояске F тр II	Н	112
Усилие в момент начала прессования, F	Н	116 314	Y 2
Усилие в момент завершения прессования, F	Н	87 807

Таблица 3

Параметры модели прессования проволоки ∅ 2,0 мм из сплава ПОИн-52 для пяти предельных скоростей истечения

Yl*/Y2*	Вариант	Параметры модели прессования						проволоки
0.016235	1	¥Р	Y2*	Y1	Y2	XI	Х2		Х4	Х5	Х6
		0.0009	0.055437	1.8	15555.77	15	80	20	1.0125	75	0.3
2.664662	2	Y1*	Y2*	Y!	Y2	X!	Х2	хз	Х4	Х5	Х6
		0.25	0.093821	500	26326.23	2.1909	80	20	6	75	0.3
3.34603	3	YP	Y2*	Y1	Y2	XI	Х2		Х4	Х5	Х6
		0,5	0.149431	1000	41930.59	2	80	25.82	6	75	0.3
3.472146	4	YP	Y2*	Y1	Y2	XI	Х2	ХЗ	Х4	Х5	Хб
		0.75	0.216005	1500	60611.35	2	80	31.623	6	75	0.3
3.545636	5	YP	Y2*	Y1	Y2	XI	Х2		Х4	Х5	Хб
		1	0282037	2000	79140.1	2	80	36.515	6	75	0.3

Входные параметры математической модели прямого прессования проволоки (прутков) из сплава ПОИн-52

Выходные параметры математической модели прямого прессования проволоки (прутка) из сплава ПОИн-52

ется в пятом в а риа н те , сле д ов а тельн о, в э том случае имеет место оптимум: V _ист = 2000 мм/с; F = 79 140 H; D_BSX = 2 мм ; д ли на за гот ов к и L = 80 м м ; д иа ме тр к он т е й н е ра D кон = 36 мм; скорость прессования V пр = 6 мм / с; полу у гол матрицы (волоки) α = 7 5 ° ; ко эф ф ициент f = 0,3.

Анализируя табличные данные (см. табл. 3), можно выявить следующую тенденцию. По ме- ре увеличения значения отношений критериев Y1*/Y2* поиск методом обобщенного приведенного градиента сводится к отысканию оптимального диаметра контейнера Dкон, т. е. поиск начинается с 20 мм и заканчивается 36,515 мм. Вариант 5 является оптимальным, так как в этом случае имеет место максимальное отношение критериев Y1*/Y2* = 3,545.

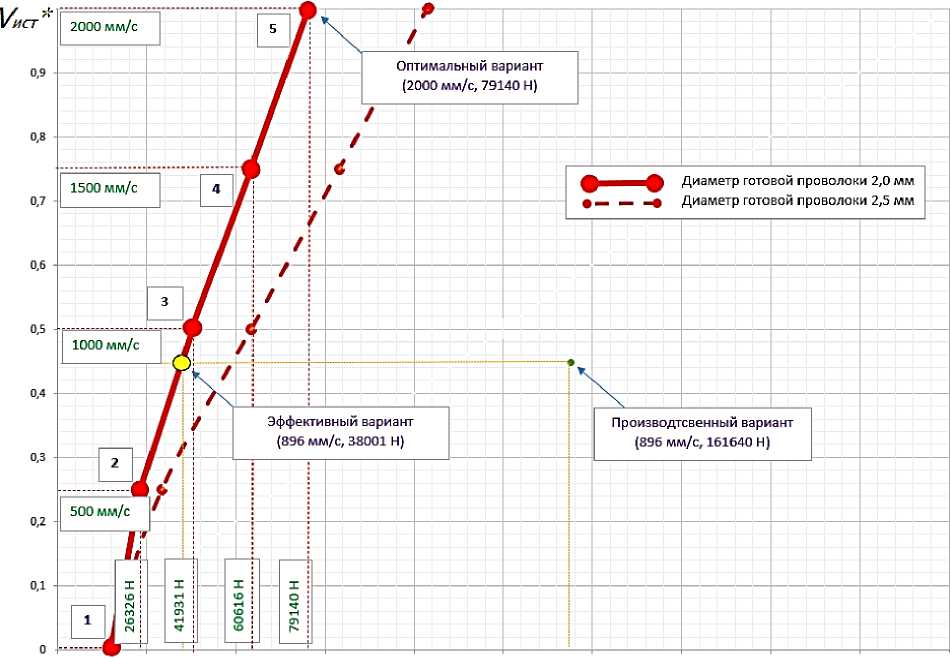
Рис. 3. Фронт Парето по пяти точкам для критерия V ист* и F при прямом прессовании проволоки из сплава ПОИн-52: 1–5 – варианты расчета оптимизационной задачи, сплошная красная линия фронта соответствует случаю выпуска готовой проволоки 2,0 мм; пунктирная красная линия фронта соответствует случаю выпуска готовой проволоки 2,5 мм; зеленая точка соответствует интуитивно разработанному производственному варианту процесса, а желтая – его эффективному варианту

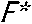
Остальные параметры принимают граничные значения: диаметр готовой проволоки D_BSX = min; длина заготовки L = max; скорость прессования V пр = max; полуугол волоки α = max; коэффициент f = min.

Если указанные пять точек нанесем на плоскость возможных оценок для критериев V ист^* и F ^* , соединим их красной жирной линией, то получим фронт Парето рассматриваемой задачи (рис. 3).

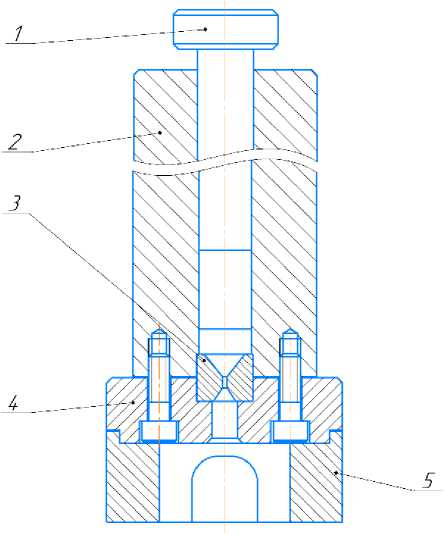
Рис. 4. Эскиз оснастки: 1 – пуансон; 2 – контейнер; 3 – матрица (волока); 4 – прижим; 5 – седло

Ранее интуитивным путем была спроектирована и изготовлена технологическая оснастка для прямого прессования данной проволоки (рис. 4). Конструктивные параметры оснастки при практическом применении обеспечивали скорость истечения сплава из матрицы (волоки) 896 мм/с, при этом усилие прессования в начальном моменте составляло 161 640 Н [3].

Если решить оптимизационную задачу для предельной скорости V ист^max = 896 мм/с, то можно снизить усилие прессования с 161 640 до 38 001 Н за счет уменьшения длины заготовки с 120 до 80 мм, уменьшения диаметра контейнера с 32 до 24 мм, увеличения полуугла матрицы (волоки) с 23 до 75°. При этом скорость прессования возрастет с 3,5 до 6 мм/с при постоянном диаметре готовой проволоки D BSX = 2 мм и коэффициенте трения f = 0,3. В результате чего производство проволоки станет эффективнее. Параметры трех процессов – оптимального, производственного и эффективного показаны в табл. 4.

Из табл. 4 видно, что по критерию Y 1^* / Y 2^* эффективность производственной технологии увеличена в 4,2 раза и только на 8 % уступает оптимальному варианту. На рис. 3 с фронтом Парето производственному варианту соответствует зеленая точка, а эффективному – желтая.

В случае выпуска готовой продукции большего диаметра фронт Парето будет изгибаться в правую сторону, как показано на рис. 3. Пунктирная линия соответствует случаю D BSX = 2,5 мм. Пять вариантов расчета координат характерных точек для новой кривой представлены в табл. 5.

Сравнительный анализ 5-го и 10-го оптимальных вариантов (см. табл. 3 и 5) позволил выявить следующую закономерность. Производство проволоки большего диаметра снижает эффективность в 1,4 раза (оценено по отношению Y ₁ ^* / Y ₂ ^* ), что отражается в увеличении усилия прессования с 79 140 до 116 314 Н. Связано это с необходимостью увеличения диаметра контейнера с 36 до 45 мм. Таким образом, повышение эффективности процесса прессования в большей степени зависит от диаметра контейнера и для изготовления проволоки увеличенного диаметра требуется большая по размерам оснастка.

Дальнейшее увеличение размера выпускаемой проволоки искажает нелинейный фронт

Таблица 4

Параметры модели прессования проволоки из сплава ПОИн-52 для оптимального (вариант 5), производственного и эффективного вариантов

Yl*/Y2*	Вариант	Параметры модели прессования						проволоки
	5	YP	Y2*	Y1	Y2	XI	Х2	хз	Х4	Х5	Х6
Л ,)4)0.5 о		1     0,282037		2000	79140,1	2	80	36,515	6	75	0,3
0,777778		YP	Y2*	Y1	Y2	XI	Х2	ХЗ	Х4	Х5	Х6
		0,448	0,576	896	161640,5	2	120	32	3,5	23	0,3
		YP	Y2*	Y1	Y2	XI	Х2	ХЗ	Х4	Х5	Х6
		0,448	0,135429	896	38001,53	2	80	24.44	6	75	0,3

Таблица 5

Параметры модели прессования проволоки из сплава ПОИн-52

для пяти предельных скоростей истечения и условии выпуска проволоки диаметром 2,5 мм

Yl*/Y2*	Вариант	Пара			метры модели прессования проволоки
0,0162	6	Yl*	Y2*	Yl	Y2	XI	Х2	ХЗ	Х4	Х5	Х6
		0.0009	0.0554	1,8	15556	15	80	20	1.0125	75	0,3
2,1516	7	Yl*	Y2*	Yl	¥2	XI	Х2	ХЗ	Х4	Х5	Х6
		0,25	0.1162	500	32604	2,5	80	22,822	6	75	0,3
2,3079	8	Yl*	Y2*	Yl	Y2	XI	Х2	ХЗ	Х4	Х5	Х6
		0,5	0.2166	1000	60791	2,5	80	32.275	б	75	0.3
2.3763	9	Yl*	Y2*	Yl	¥2	XI	Х2	ХЗ	Х4	Х5	Х6
		0,75	0,3156	1500	88562	2,5	80	39,528	6	75	0,3
	10	Yl*	Y2*	Yl	¥2	XI	Х2	ХЗ	Х4	Х5	Х6
1 2,4125		i	0.4145	2000	116314	2.5	80	45.644	б	75	0,3

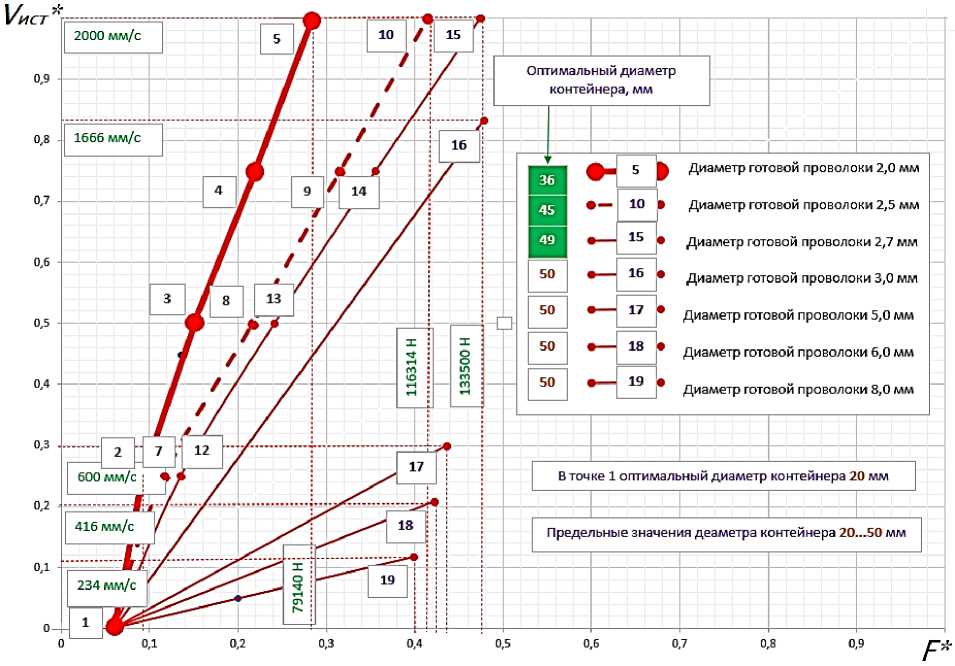
Рис. 5. Семейство кривых Парето для проволоки диаметром от 2,0 до 8,0 мм

Паре то, с м е щ а я е го в п ра во ( ри с . 5) , а п ри до сти ж е н ии д и а м е тра п ров о лок и в 3, 0 мм ли н ии ф онта п е р е ме ща ю тс я в н и жн юю ча с ть к оорди н а тн ой пл оск ос ти , что с в яз ан о с д о с ти жен и е м верхней п ре де льн о й гра н и ц ы п а р а ме тр а D кон = 50 мм.

Рассматривая графические зависимости (см. рис. 5) можно обнаружить, что область эффективных процессов прямого прессования находится в верхнем левом квадранте коор- динатной плоскости. Характерной особенностью этой области также является и то, что в ней выполняется условие Vист* > 0,5 и F* < 0,5.

Дальнейший анализ оптимальных решений позволил установить наиболее важный параметр. Оказалось, что наибольшее влияние на эффективность прессования оказывает диаметр контейнера. Именно его размеры главным образом определяют усилие прессования и скорость истечения сплава из матрицы.

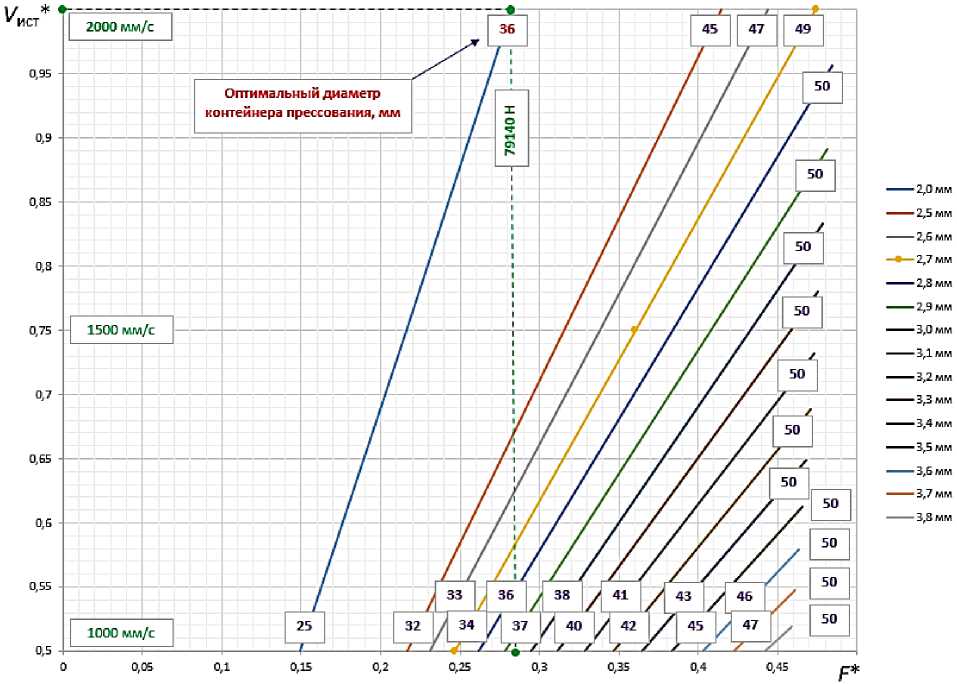
Рис. 6. Номограмма для определения оптимального диаметра контейнера прессования ( D кон ) *

в зависимости от скорости истечения ( V _ист ^* ) и заданного диаметра готовой продукции ( D_BSX )

Целе с оо б ра зн о пос троить н омогр а мму , п озв оляю щую оп ред е лят ь оп ти ма льный д и а мет р к онтейн ера прес с о в а н и я в за ви симос ти о т с к орос ти и с т е че н и я и за д а н н ого ра зм е р а в ы пу с к ае мой продукци и ( ри с. 6) . На г ори з о н тальн ой ос и у к а за н ы зн аче н и я н орма ли зован *

н ого к ри т ери я усил и я п ре с с ов а н и я F , чем мень ш е е г о зн а че н и е , тем н и же у с и ли е п рес сов а н ия. П о верт и к альн о й ос и п ри в е д е н ы зн а ч е н ия норма л и з ов а н н ого к ри те ри я ск орос ти истечения V ист^* , с оотв е тс тв е н н о, че м в ыше е г о зн а чен и е , т е м б ольш е с к орос ть и с теч е ни я спла в а и з м а т ри ц ы и п ро и з в оди те льн е е п ро ц е с с . С е ме й с т в о л и н ий п ок а зы в ае т опти ма л ьн ый д иа ме тр к он тей н е ра д ля провол ок и от 2, 0 д о 3,8 мм в з ави с и мос ти от с к ор ос ти и с те че н и я и л и у с и л и я прес с ов а н и я. На п ри м ер, п ри п рои з в одс тв е п ров оло к и д и а м е тром 2, 0 мм оп тимал ьн ый д и а ме тр к он те йн е ра б у д е т с оотв ет ствов а ть 36 м м, а у с и л ие п ре сс ов а н и я составит 79 140 Н п ри с корос т и и с те чен ия 200 0 м м/с . Так ж е можн о обра ти ть в н и ма н и е и н а то, что, н ачин ая с д и а ме тр а п роволок и 2, 8 мм, опт и мальн ым б у д е т д и а м е т р к он те й не ра 5 0 мм

(максимально допустимый условиями поставленной задачи F ^max = 280 000 Н).

Номограмма позволяет не только определить оптимальные условия изготовления проволоки заданного диаметра, но и выбрать эффективный режим прессования при имеющемся типоразмере контейнера путем определения эффективной скорости прессования и истечения материала.

На основании проведенного математического анализа сформулированы следующие выводы.

• 1.    Впервые изучен процесс прямого прессования проволоки из сплава ПОИн-52, учитывающий повышение его эффективности по двум критериям: скорость истечения сплава из матрицы V ист и усилие прессования F .

• 2.    Методом обобщенного приведенного градиента найден оптимум при максимальной скорости истечения и минимальном усилии прессования ( V ист^max = 2000 мм/с и F = 79 140 Н) технологии изготовления проволоки диаметром 2,0 мм ( Х 1 ) из сплава ПОИн-52 с параметрами: длина заготовки L = 80 мм ( Х 2 ); диаметр

• 3.    Достичь снижения усилия прессования с 161 640 Н до 38 001 Н без изменения скорости истечения ( V ист^max = 896 мм/с) можно за счет уменьшения длины заготовки с 120 до 80 мм, уменьшения диаметра контейнера с 32 до 24 мм, увеличения скорости прессования с 3,5 до 6 мм/с и полуугла матрицы (волоки) с 23 до 75° при постоянном диаметре готовой проволоки D BSX = 2 мм и коэффициенте трения f = 0,3.

• 4.    Технологическим параметром, относительно которого можно оптимизировать про-

• цесс прессования, является диаметр контейнера. Такие параметры процесса, как длина заготовки, коэффициент трения для снижения усилия прессования, должны находиться на минимальном значении, а полуугол волоки (матрицы) и скорость прессования – на максимальном значении, допустимом технологией процесса. При этом диаметр готовой проволоки (прутка), как правило, жестко задается заказчиком.

• 5.    С целью выбора оптимального значения диаметра контейнера в зависимости от диаметра готовой проволоки построена номограмма.

контейнера D кон = 24 ( Х 3 ); скорость прессования V _пр = 6 мм/с ( Х ₄); полуугол матрицы (волоки) α = 75° ( Х 5 ); коэффициент f = 0,3 ( Х 6 ).