Оптимизация процессов эмиссии летучих органических соединений из океана в атмосферу в период цветения фитопланктонов

DOI:

Как сообщается в работе [1], процессы эмиссии из океана летучих органических соединений в атмосферу изучены не полностью. Согласно [1], океанические эмиссии метанола, ацетона, ацетальдегида, изопрена и диме-тилсульфида (DMS) зависит от величины фотосинтетически активной радиации (PAR) и некоторых биологических параметров. Исследования на границе океан – атмосфера, проведенные в [1] показали, что после цветения фитопланктонов летучие органические соединения, измеренные протонным масс – спектрометром (PTR-MS) в небольшой замкнутой акватической экосистеме (mesocosm) имели следующую закономерность: изопрен и асе-тальдегид эмитировался в количестве, хорошо коррелирующимся количеством света (r AVCORR,ISOPRENE = 0,49; r AVCORR, ASETALDEHYDE = 0,70), а также количеством фитопланктонов. DMS также эмитируется в атмосферу, однако количество DMS значительно не коррелирует величиной света (r_AVCORR,DMS = 0,01).

Исследования, проведенные в [1], показывают, что PAR и биологические факторы должны быть использованы при оценке влияния океанов на баланс летучих органических соединений в атмосфере.

Прежде всего отметим, что изопрен (CH2=CH-C(CH3)=CH2) является биогенич-ным углеводородом, эмитируемым деревьями, травой и океаническими фитопланктона-ми. Целью эмиссии является противодействие абиотическому стрессу. Изопрен играет важную роль в формировании атмосферного озона, аэрозолей и облаков.

Согласно работе [4, 5, 8, 9, 11], существует корреляционная связь между изопреном и концентрацией хлорофилла а в морской воде. Графически такая корреляционная связь отображена на рисунке 1 [3]. Как видно из графиков, приве- денных на рисунке 1 максимум концентрации изопрена находится на более низкой глубине, чем максимум концентрации хлорофилла.

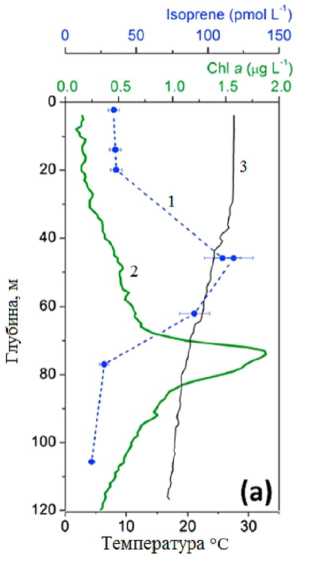
Рис. 1. Графическое отображение наличия корреляционной связи между изопреном и хлорофиллом в океанской воде в зависимости от глубины и температуры. Цифрами указаны:

• 1    – кривая изменения концентрации изопрена по глубине;

• 2    – кривая изменения концентрации хлорофилла по глубине; 3 – кривая изменения температуры воды по глубине [3]

Согласно [3], справедливы следующие регрессионные уравнения между количеством изопрена и концентрацией Chl в морской воде

ISO = 37,9 • [ Chla ] + 17,5; R ² = 0,37       (1)

ISO = 15,1 ^ [ Chla ] + 18,4; R ² = 0,55       (2)

Согласно работе [10], существует прямая корреляция между концентрациями изопрена и хлорофилла в воде (рис. 2), зависящая от сезона. Так, для Северного моря в июне r2 = 0,62 , а в апреле r2 = 0,43.

Согласно работе [7], важнейшими факторами, влияющими на эмиссию изопрена в атмосферу являются скорость ветра и интенсивность фотосинтетически активного света (400 – 800 нм).

На рисунках 3 и 4 показаны соответствующие скатерограммы зависимости концентрации изопрена в атмосфере над Средиземным морем. Cогласно [3], при скорости ветра ниже 4 м/с концентрация изопрена уменьша- ется по экспоненциальному закону, а при значениях выше 4 м/с не изменяется (рис. 3). Зависимость концентрации изопрена в атмосфере над морем от интенсивности света также экспоненциальна (рис. 4).

В настоящее время существуют несколько математических моделей, отображающих процесс эмиссии в атмосферу морского изопрена. Например, согласно модели, изложенной в [6], эмиссионный поток может быть вычислен по формуле

F voc = k w (U , SST ) • Chla • b , (3) где k_w – коэффициент передачи изопрена, зависящая от скорости ветра U и поверхностной темпе-

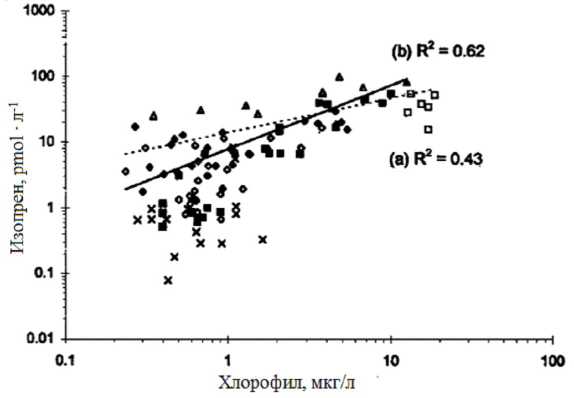
Рис. 2. Концентрация изопрена в морской воде как функция концентрации хлорофилла в Северном Море (июнь – обозначены треугольниками), (апрель – обозначены полыми ромбами), (декабрь – обозначены крестиками), а также в море Беллингкаузена (черные ромбы), в береговой зоне Северного моря (полые квадраты)

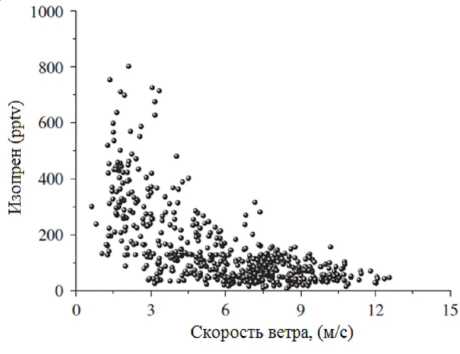
Рис. 3. Зависимость концентрации изопрена над морем от скорости ветра

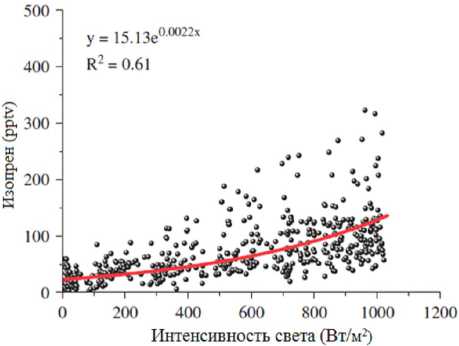
Рис. 4. Зависимость концентрации изопрена над морем от интенсивности света

ратуры моря; b – коэффициент пропорциональности; Chla – концентрация хлорофилла а в морской воде.

Согласно работе [2], общее колонное количество эмитированного в атмосферу изопрена EISO может быть вычислено по следующей формуле

H max

E iso = SA ■ H max ■ Chla ■ F iso ■ J Pdh (4)

где SA – площадь поверхности рассматриваемого участка, м2; FISO – эмиссионная фракция, то есть фракция водной колонны, эмитирующей изопрен; Hmax – общая глубина водяного слоя, способного продуцировать изопрен.

H

max

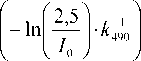
где: I 0 - интенсивность солнечной радиации; k 49'0 -коэффициент диффузного ослабления в воде.

Далее, в настоящей статье рассматриваются вопросы оптимального выбора таких внешне воздействующих факторов как I0 и U, при котором можно было бы минимизировать суммарную эмиссию изопрена в атмосферу с учетом моделей (3) и (4). Модель (3) с учетом графиков, представленных на рис. 3 и 4 при SST = const можно представить в виде

_ u

F vocm = k • e a ' e" 2" 0 ' Chla ,          (6)

где k = const; U – скорость ветра; a = const; a2 = const.

Интегрируя (6) в пределах I0 = 0 – I0max имеем

I о max        _ ^U

F oc m . ин = J k ■ e    ■ e a 2 ' I 0 ■ Chla ' dI о (7)

Так как исследуется оптимальная взаимосвязь параметров U и I₀, при которой F_VOC.m.ин достиг бы минимума, в функционал (7) вводим функцию U = U(I₀), на которую налагается следующее ограничительное условие

F = Ju(Iо)diо = C,; C, = const,

В простейшем случае условие (8) подразумевает наличие функций U(I0) в виде

U, = Uo, + k, I о

U2 = U02 _ k210

где U01, U02, k1, k2 = const.

Общий вид функций (9), (10) показан на рисунке 5.

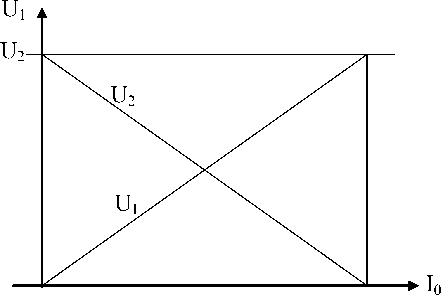
Рис. 5. Общий вид функций U1 и U2 определенных выражениями (9) и (10)

С учетом выражений (7) и (8) можно сформировать следующий функционал безусловной вариационной оптимизации

• ¹    Omax        _ ^U ( ¹ 0 )                                    ¹ Omax

F o = J k - e ^a' -e‘ 2 ' ^{1 0} -Cha-dl о + X J U ( I o ) di о - C , о                                                       о

где λ – множитель Лагранжа.

Согласно уравнению Эйлера решение вышеуказанной оптимизационной задачи на экстремум должно удовлетворить условию d ^

_ U ( I » ) k - e    a'    e a^{a 2} ' ^{I о}

■ Chla + X\U (Iо) - C, ]> dU(I0)

= о (12)

С учетом выражений (8), (12) можно показать, что минимальное значение F0 обеспечивается при линейной зависимости между U и I0, то есть

U = C₂ I₀ + C₃, где C₂, C₃ = const

Решим аналогичную оптимизационную задачу применительно к модели (4) и (5). С учетом выражений (4) и (5) имеем

E iso = SA • ln l | • • Chla • F iso • P • H max (13) V 2,5 7

При выводе формулы (13) принято упрощающее предположение о том, что Р не зависит от h.

С учетом информации, представленной на рис. 3 функционал (13) модифицируем в следующем виде

_ U ( I 0 )          I I \

E =e ^{a 1} Л-lnl — U^-1 -Chla-F PH

E ISO . m e ^{SA ш} ~ - k 490 Chla F ISO P H max⁽¹⁴⁾

V ^2,5 7

Выражение (14), при перепишем как

U ( I 0)

Eisom = C г e a¹ •ln|^^ !• Chla       (15)

V ^2,5 7

где C4 = const

На основе выражения (15) сформируем целевой функционал

I 0 max            U ( I 0 )

I

i                    V ^2,5 7

0 min

С учетом выражений (8) и (16) сформируем оптимизационную задачу безусловной вариационной оптимизации

U ( I 0 )

a ¹ • ln^{|0 ,} °- ]• Chla • dL + V 2,5 7           ⁰

¹ 0max          _^

^E ISO m .0 = J ^C 4 • e

¹ 0 max

+ X J U ( 1 0 ) dI 0 _ C 1

_ 1 0,m„

Можно показать, что при оптимальной зависимости

U ( 1 0 ) = In

C • ln l - ^ ^ ]• Chla . ⁵ V 2,5 7         .

где C5 = const функционал (17) достигает минимума

Таким образом, обе рассмотренные модели эмиссии изопрена в атмосферу обладают экстремальным свойством, точнее говоря минимумов интегрального значения эмитированного изопрена в некотором интервале величин фотосинтетически активного оптического излучения Солнца при соблюдении выявленных оптимальных функций взаимосвязи между интенсивностью оптического излучения и скоростью ветра При этом выявлено существенное несовпадение видов этих функций для двух рассмотренных моделей процесса эмиссии изопрена из океанических вод в атмосферу при наложении некоторого фиксированного функционального ограничения на искомую оптимальную функцию Такое различие в выявленных оптимальных режимах эмиссии указывает на необходимость дальнейшего усовершенствования математических моделей потоков летучих органических соединений, исходящих из океанических вод