Оптимизация процессов контроля погрешности идентификации изображения микрообъектов

DOI:

В настоящее время, существует множество работ, посвященные интеллектуализации и автоматизации функции идентификации, распознавания, классификации изображения микрообъектов таких, как пыльцевые зерна, одноклеточные микроорганизмы медицинских объектов, картинки полезных минералов в горной массе и других предметных областях знания [1].

Микрообъекты имеют сложные структуры, характеризуются большой вариабельностью точек и признаков, высокой зашумленностью и наличиям дефектных изображений из-за смази, сдвигов точек и влияния других факторов. Все эти факторы приводят к искаженным результатам идентификации микрообъектов [2].

В существующих системах микрообъекты регистрируются, анализируются, визуализируются в ручном режиме реального времени, которые не позволяют оперативно распознавать и классифицировать изображения с сложными динамическими структурами [3].

Востребовано исследование, которое направлено на развитие, совершенствование существующих подходов и методов, а также разработку новых механизмов оптимизации процессов идентификации, распознавания, классификации изображения микрообъектов. Востребованность этого исследования состоит еще в том, что микрообъекты отличаются друг от друга своей внешней структурой, требуется быстро и точно определять разновидности, принадлежность объектов к какому-либо классу по их геометрическим формам и другим специфических характеристикам.

Таким образом, необходима компьютерная система, способствующая обеспечению большей оперативности учета изображений исследуемых микрообъектов, формированию их в базе данных, в базе знаний со статистическими параметрами (математическое ожидание, дисперсии, корреляционные характеристики, функции вероятностей распределения), динамическими свойствами (вариативность статистических параметров), специфическими характеристиками (текстурные, фрактальные особенности и др.). Такая система освободит специалистов от утомительного перерасчета микрообъектов большого количества, пересмотра больших объемов данных. В публикациях по этому направлению исследования отмечается, что существующие стандарты крайне недостаточны, а также некорректны для принятия их в качестве методологии идентификации, распознавания, классификации микрообъектов [4].

Необходимо, чтобы система проводила оперативный учет и анализ изображения со слайдов,     представляемых     оптическими микроскопами. Кроме того, требуется удаление инородных частиц, мусора, помех, размытия точек с целью значительного уменьшения погрешности идентификации изображений [5].

МЕХАНИЗМЫ ОПТИМИЗАЦИИ ИДЕНТИФИКАЦИИ, РАСПОЗНАВАНИЯ И КЛАССИФИКАЦИИ МИКРООБЪЕКТОВ НА ОСНОВЕ ИСПОЛЬЗОВАНИЯ СТАТИСТИЧЕСКИХ И ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК ИЗОБРАЖЕНИЙ

В работе решение задач идентификации, распознавания и классификации изображения микрообъектов существенно усиливается за счет построения и реализации инструментов выделения, сегментирования фрагментов и контура, фиксирования опорных точек, связывания точек перепадов, переходов, а также использования статистических и динамических характеристик информации [6, 7].

Реализован подход, который направлен на построении новых механизмов – моделей, алгоритмов,    программных    инструментов обработки информации микрообъектов, в которых учитываются внутренние и внешние воздействия, присутствия шума (помех), дефектов из-за сдвигов точек и другие отрицательные факторы, приводящие к значительным    значениям    погрешности идентификации изображений [8, 9].

Разработан механизм оптимизации процессов идентификации   микрообъектов,    который направлен на использование ансамбля статистических - трендовых моделей для адекватного      описания      изображения.

Инструменты этого механизма идентификации микрообъектов основаны на применении принципов декорреляции и редуцирования избыточных (нулевых) точек контура во временном ряду последовательности точек изображения [10].

Ансамблевые модели включают 47 трендовых зависимостей,      моделей      адаптивного экспоненциального сглаживания (Р. Брауна), авторегрессионного анализа, статистического предсказания по одной, двум и п - точкам [11, 12]. Эффективность этих моделей проверена по 14 наборам обучения и по критерию минимальной среднеквадратической погрешности.

Оцениваются результаты реализации вычислительных схем инструментов описания и регулирования переменных точек контура, отбора опорных точек, контроля погрешности идентификации для рассмотренных моделей.

Эффективность инструментов оптимизации идентификации микрообъектов оценены также по коэффициентам трудоемкости и стоимости обработки информации изображения. Рассмотрен вариант выбора адекватного алгоритма путем эвристического подбора на основе исходных наборов обучения без применения механизма оптимизации.

Доказано, что низкая эффективность алгоритмов идентификации обуславливается при присутствии случайных вспышек, воздействия помех, недостаточности априорных сведений.

Для повышения эффективности механизма идентификации микрообъектов включен инструмент декорреляции путем определения коэффициентов автокорреляции. При этом, инструмент редукции точек в наборе обучения начинает с пустого множества, затем отыскиваются все возможные одиночные точки. Исключается та точка кривой контура, которая имеет значимый коэффициент автокорреляции.

Эффективность реализованных инструментов оптимизации процессов идентификации повышается на основе синтеза алгоритмов статистического контроля погрешности на основе использования следующих правил: последовательного анализа, Байесовской оценки, правило ±3a, контроля по доверительному интервалу [13, 14].

Инструмент оптимизации контроля погрешности при идентификации изображения микрообъектов применяет модели авторегрессии (АР) и проводит контроль информации по нижней и верхней границам доверительного интервала

S^y-^22.

‘Н - ^ j - t kpJ Т^Т^;

।      ^^Z^-Z²^

1B - Aij + tkp J ^N^y , где у^- АР; yi=AtjXi - выход АР; A,j -коэффициент АР; xf - значение точек контура; у - N — к - число степеней свободы, к — inf{kl,kj], к, и kj - корреляционные коэффициенты i -й, j -й точек контура; tkp -критерий Стьюдента [15].

ОПТИМИЗАЦИЯ КОНТРОЛЯ

ПОГРЕШНОСТИ ИДЕНТИФИКАЦИИ МИКРООБЪЕКТОВ ПО ГРАНИЦАМ ПРИРАЩЕНИЙ ВРЕМЕННЫХ РЯДОВ ТОЧЕК ИЗОБРАЖЕНИЯ

Разработан инструмент оптимизации контроля погрешности идентификации изображения, который основывается на использовании нижнего а _а — x и верхнего а _а + у порогов, разделяющих множество значений переменных точек контура {P j } на подмножества разрешенных значений {P _p } а _а — x < P _p < а _а + у и запрещенных значений {P 3 } a3_am;_па а _а + у < ^ 3 <  ^amax .

Когда точка P j принадлежит подмножеству {P_p}, то ее значение считается разрешенным. Когда значение P j принадлежит подмножеству запрещенных значений {P 3 }, тогда значение точки считается не разрешенным. Инструмент при контроле оставляет необнаруженными ошибки двух родов. Вероятность ошибки первого рода

{W-^.

Вероятность ошибки второго рода

P{a _t - P j .P , e {P 3 }}; P ₂ - P{a _t * Py.P , e {P 3 }}-(1 — ^p )[1 — X^a_a2Z /-x _/S f(a _i )].

Представляет интерес исправлении искаженных значений, т.е., значений не разрешенных точек изображения.

Инструмент контроля погрешности A°_n .

Обозначим, диапазон значений точек a контура изображения через aminmax. Значения точек P эталонного контура изображения верными у - Pk (^ ()),  т.е.

считаются подобласть

запрещенных значений точек {P3} считается пустой.

Инструмент контроля погрешности А^_п .

Область значения параметра точки a в трех подобластях идентификации разбивается на нижний x и верхний у пороги контура и соответствуют следующим правилам:

xx,  при  amin - Pmin у - \р,  при  x < P < у;

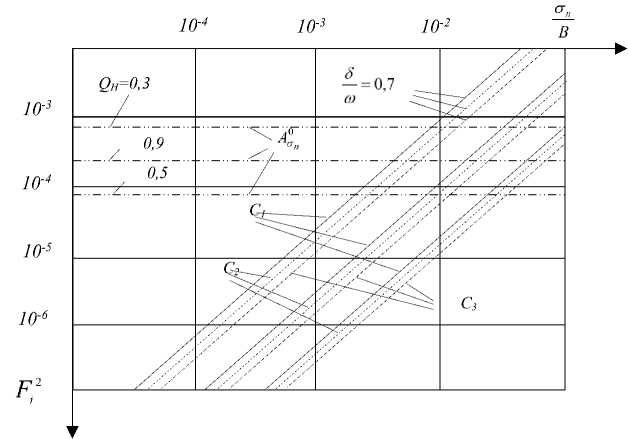
(у,  при   у

max

Значение точки контура, которое выходит за границы разрешенной подобласти сглаживается путем отождествления с верхней или нижней границами контроля. Инструмент контроля погрешности Л"п. Значения погрешности точки контура изображения контролируется по следующим правилам:

(Р,  при х < Р <у;

{аа,  при  amin = Pmin < Р < х;у < Р < Pmaxmax т.е. недопустимые значения точек контура Р сглаживается путем отождествления со средним значением аа.

Инструмент контроля погрешности Б^. Пусть точки контура изображения описываются случайным процессом а( t) с двумерной функцией плотности распределения вероятностей ((«1, а₂, т), математическим ожиданием а_а, дисперсией о^ и коэффициентом корреляции В(т) (здесь т — t/* — t _к-1 шаг квантования по времени). Обозначим через Да_к разность (приращение) а_к— а_к-1 между к и (к — 1)-м дискретными точками последовательности (0 < Дал < В) - входного изображения и (0 < ДРл < В) эталонного.

По оси множества значений точек контура {ДР} установим отрицательную (—Дх) и положительную (Ду) границы, которые разделяют множество приращений {ДР} на разрешенное {ДР*}, где —Дх < ДР_р< Ду и запрещенное {ДР3}, где —В < —ДР3 < —Дх, Ду < ДР3 < В подмножества.

Принцип контроля информации заключается в следующем: значение точки контура а_к считается разрешенной, если ДР_к £ {ДРр} и неразрешенной, если ДР_к£ {ДР3}.

Не разрешенное значение точки исправляется по правилу

₌ (Рк, если ЛРк £ {Р_р};

^{Ук {}Рк-1, если ЛРк £ {Рз}.

Недопустимое значение точки исправляется путем отождествления со значением предыдущей точки Р_к-1 контура.

Инструмент контроля погрешности Вап. По оси ДР* устанавливается отрицательная (—Дх*) и положительная (Ду*) границы контроля значений погрешности идентификации точки, которые разделяют множество значений точек контура {ДР*} на разрешенное  {ДРр} и запрещенное {ДР*} подмножества.

Инструмент значения точки контура считает разрешенной, если оно ДРк* £ {ДР*}, —Дх* < ДРк* < Ду* и недопустимой, если ДРк* £ {ДР*}, —В < —ДРк < —Дх*,Ду* < ДРк < В.

Исследована    эффективность    следующих инструментов     контроля     погрешности идентификации    с    такими    моделями статистического предсказания, как В^  - со ступенчатой экстраполяцией; В^ ,В^  - со статистической экстраполяцией, соответственно, по одной и двум предыдущим точкам.

Для инструмента с предсказанием значение недопустимой точки исправляется по следующим правилам

₌ ГРк, если ЛР*_к £ {Рр};

^Гк   [р* если ЛРк£{Р3].

Исправленное значение точки Рк — Р_к-1 - для алгоритма В^; Рк*- алгоритмов Вк2_п,В;3_п.

ОБЩЕЕ РЕШЕНИЕ ЗАДАЧИ ОПТИМИЗАЦИИ КОНТРОЛЯ ПОГРЕШНОСТИ ИДЕНТИФИКАЦИИ ИЗОБРАЖЕНИЯ МИКРООБЪЕКТОВ

Получены общее и частные решения задач.

Решение задачи по инструменту А¹*^.

Среднеквадратическая            погрешность идентификации при использование этого инструмента оценивается, как

°п - ^М[(У ^— РУ] - ^Ма^Р;Р£{Р_р}[^{(а —} РУУ + ^М а* $■ $£{$₃}^{[(а — х}УУ + ^Ма^Р;Р£{Р3}[^{(а — у)}2] + ^+Ма=Р;Р£{Р₃};Р<х^{[(а — х}УУ + ^Ма=Д;Д£{Д₃};Д>у^{[(а — у)}2^].

Математическое выражение запишем в явном виде:

On

— ^J^^da^ (a —x)2d/? + J (a —/?)2d/? + J (a —y)2d/?] + +(1 - P) [/^(a — x)2co(a)da + ^ (a — y)2w(a)da].

После вычисления интегралов и замены

M(a²) — о² + a2 и M(a) = a_a выражение (1)

примет вид:

Pr

°n=B [x(o2 + a2 — 2a„x + x2) + (B — y)^ + a2 + aay + y2) + ^(y — x)(3o2 + 3a2 — 3a„x —

—3a2y + x2 + y2 + xy)] + (1 — P) [j (a — x)2w(a)da + J (a — y)2w(a) da]

Приравняв к нулю, частные производные по пределам порогов x и y от среднеквадратической ошибки, получаем уравнения оптимальных порогов.

Из этих уравнений находятся экстремальное значение среднеквадратической погрешности инструмента для различных сочетаний значений порогов x и y.

Решение задачи по инструменту Л₂ .

Среднеквадратическая           погрешности претерпевает ряд преобразований и записывается в виде

°п - М[(У — Ю2] - M2*£;£e{£p}[(a — Ю2] + M2*^;^e{^3};^y[(a — a2)2] +

^+M2=^;^e{^₃};^[^{(a — a}2^{)2] + M}2=^;^e{^₃};^>y^{[(a — a}2)2^].

Затем переписывается в виде

(1 — P) [j (a — a2)2w(a)da + J (a — a2)2w(a)da]

после вычисления интегралов в несложных преобразованиях принимает, как

O2 - p [xo2 + (B — y)^2 + j(y — x)^ + 3a2 + x2 + y2 B                 3

— 3a2x — 3a2y + xy)] +

+(1 —P)[o22 —J (a — aa)2w(a)da].

Определив частные производные Д^т — 0; “р" —

0 из выражения, находим уравнение оптимальных порогов механизма А^

о         о        1

"(x) — "(y) —

Решение задачи по инструменту  Б_СТп.

Погрешность контроля оценивается, как

°2 ^{— M}2_k*£_k;^_ke{^p}^[(afc ^—^k^{)2] + M}2_k=p_k;AP_ke{Ap₃}^[(ak^—^fc-1)²] ^{+ M}2_k*£_k;^_ke{4£₃}^[(ak ^—РкУ].

Выражение среднеквадратической погрешности механизма определяется в виде

о?2 — — J w(^a)d(^a)[^a2(B — 4x) + -(4x + 4y)(3^a2 + 3^a^x — 4a4y + 4x2 + 4y2 — B a                          3

-AyAx) + (В — Ay)Aa²] + (1 - P)

к-Г

-Дх

Aa2u(Aa)d(Aa)

]

Решение задачи по инструменту В°.

Инструмент с линейным предсказанием задается моделью вида L(t) - Yh=irkP(tk), rk — весовые коэффициенты; L(t) - экстраполирующий многочлен, который зависит от интервала экстраполяции и значения Pk в экстраполируемых точках.

Решение задачи проведено для ступенчатой и статистической экстраполяции по одной и двум предыдущим точкам, которые задаются в виде

L₀(tk) = Mk-j + A?(tk-1); L1(tk) = 5) Wk-0 - a_a] + a_a; °a

^L2^(tk)

_ °ав(2т)-В^а(т) _n^       оав(т)-В(т)В(2т) _n^   _A   _  [B(2t)-B(t)

=  °a-B2(T)  ^^{(tk-2) +} -^-в²^^^-1) ^{- a}«[ °a-_B(T) -

^1],

где т - интервал корреляции.

Среднеквадратическая          погрешность экстраполяции значений  параметра точки определены для: ступенчатой модели в виде -°ла* - 2[aa - В(т)]; для статистической модели В2(т)

по одной точке в виде - Од * -ri--—; для “           °а статистической модели по двум предыдущим точкам в виде о2а>

2 _ °а2В²(т)-2В²(т) + °аВ²(2т)

“             °а-в^а(т)         ■

Общее математическое выражение для получения оценке среднеквадратической погрешности инструмента В°_п запишется в виде

^h - ^M[(Yk ^{- a}k^)2]- ^Ma_k^p_k;APpe{Ap^,_p}^[(ak ^{- P}k^{)2] + M}a_k=p_k;ap_ke{apl}[^(ak ^-Pk)²] ⁺

^+Ma_k^p_k;ap^t_ke{ap^}^[(ak - Р’к')²]-

Получены оптимальные границы контроля, математические выражения оценки минимальной среднеквадратической погрешности идентификации точек.

Математическое выражение среднеквадратической погрешности контроля точек задается, как ri - M[(Yk - P^2] - Mak^kMkeWP}[(ak - P^2] +

^+Ma_k=p_k;AP*_ke{AP^k}^[(ak ^-Pk)^{2 + M}a_k^p_k;AP^ke{AP*}^[(ak ^-Pk^Y                    ⁽²⁾

Выражение распишем согласно правилам (2), которое представляется в виде p    В                         у                    В(+да)

ah - I u(a) II   (a-a_a)²dp+l (a-p^dp+I    (a

Q       ^В  0(-да)                   х                   у

-

a_a)²dp] da +

+(1 - P)[I_Q(a - a_a)²M(a)da - ^(a - a^u^da].                   (3)

Экстремальные значения среднеквадратической погрешности идентификации определяются следующим образом

0 ri

^- в [^rii ⁺ l^(-2aH 1^п^°т)^{] + (1 - p)}|°и ^-i_a^_°^{(a - a}H)^2u

(a)da].

При этом, использован способ вычисления интеграла вида

Ii = Q+(a-a_Hy

—L-g-ta-anf/Zah^. n2hoh

При t = (a - aH)/V2aH,  da = j2oHdt,а нижний и верхний  пределы  интеграла,

Xу соответственно, равны t = —f—; t = -f—.

^{,        H}     J^H  ¹¹   ^2a_H

Для вычисления интеграла (6) использована функция аппроксимации Лапласа в виде

11=^ ^-^1п^ (1 - ^Г - ^1п^).

Подставив значение интеграла (5) в выражение (4) и после несложных преобразований, х = у = ±2оН определяется минимальное значение среднеквадратической погрешности, допускаемой инструментом [16, 17].

Частные решения задачи оптимизации контроля погрешности при идентификации изображения микрообъектов. Рассмотрены различные функции распределения вероятностей. Приведем оптимальные границы контроля при нормальном законе распределения для инструмента В_а:

{-[1- В (тЖп^-В^}², (6)

где оН - погрешность предсказания; В(т) -автокорреляционная функция предсказываемой последовательности; т - предыстория предсказания.

Подставляя значение границ контроля (6) в выражение (2), находим экстремальное значение погрешности:

о

Оп = 2 [1 — В (т)]ап

■

, ^4п[1- В (т) oh

1п~-----------------

1-Р

X

f^4п[1-В(t)]qh _|_ ^ ^4п[1-В(г)]ан

(     1-Р                1-Р

1}}

Получены также решения задач для логнормального, экспоненциального распределений, и законов Вейбула, Релея [18, 19]. Однако, эти результаты представляются трансцендентными уравнениями, сложность выражений которых связана с привлечением

7-точечной   b_t =   (-f- + Mf- -

75f-1 + 344f - 75f_i+1 + 12f_i+2 - f^.

Установлено, что при идентификации изображения микрообъектов на основе базиса сплайнов    с    увеличением    количества численных методов.

используемых точек уменьшается значение

ОПТИМИЗАЦИЯ КОНТРОЛЯ

ПОГРЕШНОСТИ ИДЕНТИФИКАЦИИ МИКРООБЪЕКТОВ С УЧЕТОМ

НЕСТАЦИОНАРНОЙ ДИНАМИКИ ВРЕМЕННОЙ ПОСЛЕДОВАТЕЛЬНОСТИ ТОЧЕК ИЗОБРАЖЕНИЯ

Исследована эффективность применения интерполяционной, экстраполяционной сплайн -функции, которые могут представлены полиномиальными или базисными моделями. Предложены инструменты, которые основаны на следующих сплайнах:

3-точечный bt=- (-ft-1 + 8ft - f^); 6

5-точечный b, = — (f- - 10ft-1 + 54ft -^10ft + 1 ■ ^ft+2)^;

погрешности, а инструмент контроля достигается с меньшим объемом вычислительных операций.

Инструменты, применяющие кубические базисные сплайны по сравнению полиномиальными дают в 1,39 раза меньше погрешность округления и выполняются в 1,8 раз меньшей методической погрешностью.

Время идентификации в 2,33 раза становится меньше по сравнению с механизмом, использующим полиномы третьей степени.

Эти преимущества механизмов идентификации микрообъектов особенно ярко проявляются при использовании инструментов с вариативным математическим ожиданием, дисперсией, автокорреляционной функцией, а также регулировании степени сплайн - функции.

На рис. 1 проиллюстрированы графики относительной среднеквадратической погрешности идентификации Fj² = о^/В, которые построены в зависимости от различных значений относительной дисперсии о_Н/В.

Графики получены при различных значениях вероятности ошибок точки Р, моделях статистического предсказания (график С1), сглаживающего фильтра (график С₂), кубического сплайна (график С₃).

Рисунок 1. График функции среднеквадратической погрешности.

Figure 1. Graph of the mean square error function.

В расчетах заданы различные значения колоколообразной функции автокорреляции.

Для наглядности график функции F^ показан для значений параметра 6/ш = 0.7,Р = 10^-3. Определено, что в таких условиях o_a(t)< 0,1, Р = 3,7 ■ 10^-3 , очень близких к практическим инструменты контроля погрешности при идентификации изображения микрообъектов уменьшают значения относительной среднеквадратической погрешности на два – три порядка.

Реализованные инструменты позволяют достигнуть требуемую точность распознавания, интерпретации и аппроксимации изображения микрообъектов.

ЗАКЛЮЧЕНИЕ

Разработана методология оптимизации идентификации, распознавания и классификации микрообъектов на основе широкого спектра инструментов использования статистических и динамических характеристик информации изображения. Разработаны механизмы идентификации микрообъектов на основе инструментов фильтрации помех, дефектных точек, применения статистических приемов контроля погрешности, реализованы инструменты оптимизации контроля погрешности точек на основе порогов допустимых значений, приращений, предсказанных значений.

Предложена методика для получения общего и частных решений задач контроля погрешности идентификации при стационарном, квазистационарном и нестационарном процессах. Разработан программный комплекс (ПК) идентификации, распознавания, классификации и систематизации изображений пыльцевых зерен, поддерживающий решения задач селекции и семеноводства зерна, анализа одноклеточных микроорганизмов медицинских объектов.

ПК включает вычислительные схемы трехслойной НС прямого и обратного распространения ошибок; алгоритмов обучения с учителем и без учителя; сети Кохонена с процедурами векторного квантования, кластеризации, сегментации и образования «скользящего окна»; инструменты предварительной обработки изображения, проведения линейного, нелинейных, комбинированных трендовых описаний, применения базис сплайн - функции, линейных и нелинейных сглаживающих фильтров, а также инструментов     контроля     погрешности идентификации. Рекомендовано применение для предметных областей геофизики, экологии, сейсмологии, радиолокации, фильтрации и др.