Оптимизация процессов разделения многокомпонентных смесей

Исследование и проектирование систем химической технологии представляет собой сложную задачу, так как при ее постановке используются нелинейные системы дифференциальных уравнений в частных производных [1–5]. Математическая формулировка таких задач и вопросы их корректности, как правило, требуют специального рассмотрения. Трудности, прежде всего, связаны с нелинейностью уравнений и сложностью граничных условий, содержащих обыкновенные дифференциальные уравнения. С другой стороны, эти трудности обусловлены многомерностью задач, поскольку технологические процессы характеризуются довольно большим числом теплофизических и конструктивных параметров. Выбор эффективной методики решения задач моделирования и управления принято считать центральным вопросом в проблеме моделирования нестационарных режимов управляемых процессов разделения.

Основным инструментом проектирования технологических процессов и систем управления является вычислительный эксперимент, включающий в себя анализ многообразия технологических режимов, по- строение их физических и математических моделей, разработку и исследование вычислительных алгоритмов, их программную реализацию и проведение серии расчетов [3].

В настоящей работе формулируются и решаются задачи анализа математических моделей процессов разделения, задачи оптимального управления и численных экспериментов с целью проектирования энергосберегающих технологий разделения многокомпонентных смесей для промышленных объектов и создания соответствующих оптимальных систем управления.

Процесс разделения многокомпонентных смесей осуществляется в ректификационных колоннах на контактных устройствах (тарелках), распределенных по длине аппарата. Технологический процесс происходит в конечном числе точек объекта, однако его можно рассматривать непрерывным по длине, поэтому для моделирования возможно применение дифференциальных уравнений в частных производных. Оценка погрешности перехода от дискретной модели к непрерывной приведена в [1]. Концентрации целе- вого продукта в жидкости x = x(l, t) и паре y = y (l, t) -управляемые параметры, они определяются в результате решения соответствующей краевой задачи.

Разделяемая смесь в количестве F = F ( t ) с содержанием целевого продукта x_F = x_F ( t ) подается в среднюю часть колонны. В нижней ее части (кубе) происходит испарение смеси, и паровой поток V = V ( l , t ), поднимаясь вверх, контактируя со стекающей жидкостью L = L ( l , t ) и обогащаясь целевым продуктом, конденсируется в верхней части колонны (дефлегматоре) и отбирается в количестве D с концентрацией целевого продукта x d = x d ( t ). Часть сконденсированного пара L d = L d ( t ) из дефлегматора возвращается в колонну для повышения качества конечного продукта. В кубе отбирается остаток в количестве W = W ( t ) с содержанием целевого продукта ^x- = ^x- ⁽ t ) (ри^{с. 1).}

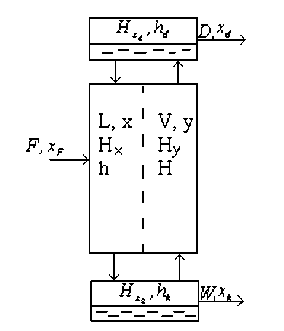
Рис. 1. Схема потоков пара и жидкости в колонне

Одним из требований к такому промышленному объекту является его способность к увеличению содержания целевого продукта в верхней части колонны и уменьшению в нижней. Важными параметрами объекта являются фазовые удерживающие способности: в колонне H_x = H_x ( l , t ),       H y = H y ( l , t ), кубе

H = H (l, t) и дефлегматоре H = H (l, t). Индек-xk        xr                                            xd        xd сы x и y указывают на принадлежность параметра жидкости или пару, k и d – кубу или дефлегматору. В колонне происходит теплообмен между жидкой и паровой средами, которые характеризуются теплосодержаниями жидкости h = h(l, t) и пара H = H(l, t); аналогично, в кубе hk = hk (t) и в дефлегматоре hB = hB (t), Hd = Hd (t). В куб подводится тепло Qk, а из дефлегматора оно отводится – Qd . Коэффициент массопередачи ky характеризует процесс массообме-на между жидкой и паровой фазами, а зависимость y* = y*(x) - равновесную концентрацию в паре. Функции x(l, t), y(l, t), xk(t), xd (t) и yd (t) могут быть скалярными (для бинарных смесей) или вектор- ными (для многокомпонентных). Более подробная физическая интерпретация математической модели содержится, например, в [5].

Используя законы сохранения массы и энергии, получим математическую модель нестационарных режимов процессов разделения для колонны, куба и дефлегматора:

^д ( ^Hx^x ) ^д ( ^Lx ) — д t        д l

= k y ( y ^- y * ) + ^{F (} t ^{) Ф} x ⁽ l ) x F ,

^д ( ^Hy y ) Л Vy )    _   .

—----+——=ky -y , дt       д l A ’

д( HyH) , д( Hxh) д(Lh) , д(VH) = ф +ф

д t          д t         д l        д l        h H’

д V д l

дL дHx дH

--+ —- + —- = Ф V + Ф,, д l д t     д t

x ( l ,0) = x o ( l ), y ( l ,0) = y o ( l ), V ( l ,0) = V _o( l ), L ( l ,0) = L ₀( l );

с граничными условиями при l = 0

д ( H_x x_k )

= L (0, t ) x (0, t ) - V (0, t ) y (0, t ) - W ( t ) x - ( t ), д t

y ^(0, t ) = ⁽ y ' ^{( x}- ) ^{- x}- ) a ^{+ x}- ⁽ t ),

( H x - h k¹ )

д t

= L (0, t) h (0, t) - V (0, t) H (0, t) - W (t) h- (t) + Qk, дHx

-= - = L (0, t ) - V (0, t ) - W ( t ),   x - (0) = x - ₀;

дt и при l = 1

д ( H x_d )

= V d y d - ( L d + D ) x d ( t ),   x d (0) = x d ,0

д t

Vd (t) yd (t) - V (1, t) y (1, t) = Ld (t) xd (t) - L (1, t) x (1, t), yd(t) = y(1, t) + Ed(y'(x (1, t)- y(1, t)),

д ( H h_d )

= V d ( t ) H d - ( L d + D ) h d ( t ) - Q d ,

д t

д ^

-fV = V d ( t ) - ( L d ( t ) + D ( t )),   V d - V (1, t ) = L d - L (1, t ),

дt

H d V d - V (1, t ) H (1, t ) = L d h d - L (1, t ) h (1, t ).

Решение       ищется       в       области

Q = { ( l , t )| l e [ 0,1 ] , t g [ 0 , T ] } , где l , t - пространственная и временная независимые переменные соответственно; T – время управления.

Считаем в дальнейшем, что    H_x = const,

H = const, kx = k = const, H, = const, H, = const, y                  y                         xk                    xd x = x (l, t),      y = y (l, t),     L = L (l, t),      V = V (l, t),

Ф H = Ф H ( l , t ),         Ф h = Ф h ( l , t ),         Ф L = Ф L ( l , t );

Ф_у = Ф у ( l,t )        - известные функции,

H = a, x + a2 y + a3 V + a4 L, h = P, x + P2 y + в3 V + в 4 L, где ai = const, вi = const, i = 1,4. При Ed = 0 пола- гаем, что yd = y(1, t), xd = x(1, t), xd (0) = x(1,0) = xd,0, Ld = L(1, t), Vd = V(1, t).

Кроме того, H_y a , + H_x P 1 = A , H_y a ₂ + H_x P ₂ = B , H y а з + H x Р з = C , H y a 4 + H x P 4 = D ⁰.

В качестве управляющих воздействий из технологических соображений выбираем потоки жидкости и пара на входах в управляемый аппарат L ( 1, t ) и V (0, t ). На эти управляющие потоки накладываются ограничения

L min <  L ( t ) < L max ,     V ^ <  V ( t ) < V ^.       (5)

J । = JJ ^{( y -@} * ) ⁺ E ^X ' f X-"й VM^? 1 ^- "й J ^dldt = q _                 ' = 1     V       ^д t 7 ' = 1 V       ³ⁱ 7]

= JJ H ^I³^³^ ' ^{dldt +} jE (^- ^{dt -X} '^dl ) z .

Q L       ' = 1 V ^d t      ^{3 i} 7 ]         SQ ' = 1

Пусть t = a ( c ), l = P ( c ) - параметрическое задание границы dQ . Тогда

J = [ Й + vf^X + ^Ь,X dldt + ^{1 J} _fi ^J L      1 :1 Vd t    d l J ' ]

Поскольку в дальнейшем для решения задачи оптимального управления будет использован метод вариационного исчисления, введем дополнительные управляющие функции u ( t ), z ( t ), с помощью которых ограничения сводятся к равенствам:

( L (1, t ) - L m, )( L max - L (1, t ) ) — U 2 = 0,

( V (0, t ) — V min )( V max - V (0, t ) ) — z 2 = 0.

В качестве критерия оптимизации выбираем интеграл, характеризующий качество продуктов разделения на выходе управляемого объекта:

T 1                                   ₂

S = JJ ( У ( l , t ) -© * ( l , t ) ) dldt ^ min,        (7)

+ J]T ( _h a' ( c ) -X ' p' C c ) ) zd a . an ' = 1

Получим вариацию J ₁ , вызванную вариациями управлений L ( 1, t ) и V (0, t ):

a J 1 = JJ

Q

:

' = 1

d H dX, дц, --+ —^L + —-д 2 ' д t д l

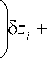
V д ^Я х

> -----о u,.

tr д U'   ¹

+ J : ( ^-a' ( o ) -X j P' C g ) ) zd a . дQ ' = 1

dldt +

Вариация для вспомогательного функционала 0 J ₂

на границе дQ вычисляется аналогично:

где 0 ( l , t ) - заданный состав выходного продукта.

Сформулируем следующую задачу: во множестве кусочно-непрерывных функций, удовлетворяющих ограничениям (5) найти такие, которые в силу системы (1)–(4) минимизируют выражение (7).

Для получения необходимых условий оптимальности воспользуемся методами вариационного исчисления. Построим скалярные функции – гамильтонианы Й uh в области Q и на границе 3Q соответственно:

5 J 2 = J

5Q _

д h            д h            д h

-------5 x (0, t ) +--5 y (0, t ) +--5 L (0, t ) + д x (0, t )           S y (0, t )          д L (0, t )

д h      n а  д h    д h      д h

+--5 V (0, t) +--5 u +--5z +--5y (1, t) + д V (0, t)           ди      дz     дy (1, t

д h            д h

+--5L (1, t) +-- дl (1, t)   v ’  д V (1, t)

. 1,   г ( д h   d X^ Y

5 V (1, t ) dt +11--1--5 x^dt +

_      ддn V^д xk     ^dt 7

Г 7 дhld

+ I+— дЪVдx (1, t)

Таким образом, вычислена вариация вспомога тельного функционала 5J = 5J1 +5J2. Используя ар-

>x (1, t ) dt - ( X k ⁰5 x k + X d °5 x (1, t ) )|

H = ( У -о * )² + ^ Х Л + Е ц , ^, i = 1                  ' = 1

где X ' , ц - множители Лагранжа;

l

h = -^ [ L (0, t ) - V (0, t ) y (0, t ) - W ( t ) x k ( t ) ] + H

гументацию вариационного исчисления, получим следующую сопряженную задачу относительно функций Лагранжа, на основе которой разработан численный алгоритм расчета оптимальных управляющих функций [1; 2; 5].

В области Q имеет место следующее:

xk

^{+ X} k ²⁾ [ У ^(0, t ) ^{- x}k ^- a ⁽ У * ^{( x}k ) ^{- x}k ) ] ⁺

+X k ” [ L (0, t ) - V (0, t ) - W ( t ) ] + X d ¹) Щ) X H x d

X [ y (1, t ) - x (1, t ) ] + X d ²⁾ [ V (1, t ) - L (1, t ) - D ( t ) ] + ^{+ y[( L (1}, t ) ^{- L} min ^{)( L} max - ^{L (1}, t ) ^)- u ² ] ⁺ + s[ ( V (0, t ) - V min )( V max - V (0, t ) ) - z ² ] ,

3X 1 +дЦ 1 = _ д t    д l	[ k ( у ) x _	7 X X —L + —— + HH V x y	X 3 C	7 AL - А1			1 + 7
				V	H x H	y 7
7 X, + U 4\й~~ V Hx	X 3 A 1 H x C J	u 4 +Ф V +Ф +     C	L a	1	u 4 R " - C в 1 ]	,

3X 2 дц₂ "дТ⁺"дТ

- u 4

2( y -9 * ) + k

( H ^x

X 2    X 3 A. X 3 B 1

H y H x C H y C J

X 2

где X k' ) , X *' ) , y , £ - множители Лагранжа.

Будем считать, что x = z 1 , y = z ₂ , V = z 3 , L = z 4 . Рассмотрим вспомогательный функционал:

V H y

X 3 b I ф _к +ф l Y

X2

H y ^{C J}    H y  V ²

7 U 4 +Ф V +Ф L

'3 I                       ^a 2

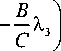
^U 4 e

C ²

дХ - дц - _ --1--= —		u	Г - 2 X - B +	Х3    ' —- а2	—
д t    д l		2	1 НУ  НУС	C 2
u 4 Х 3 ( —	—а - C	+ а 4 )   Х - а - ( ф С ( V		+Ф L ) —
Х 3 и 1 а 1 —— C	X ,	^ и 4 х	+ Фи +Ф/, ----V-----L а3 C 3	u ^ в Т с в - 7]	,
дХ 4 +5^ д t    д l	= —	-u 1- Гх, — х3 A Xх - в2 u _ Нх X 1   3 С J С 22			+
Х + "С u 4	( в -	— в 4 ) + С^ в - (ф V +ф L ) +
Х - и 1 в 1 + C	Х 3	u 4	+ ф V +ф L ex	u ^ Т1 с в 4 7]
			С      4		.

В этой системе неизвестные ц i или X i ( i = 1, 4) исключаются с помощью соотношений

Х 1 г ц +-- L 1 _H x

Х2 v ц2---+

² H y

-

X - AL

-

V а1 - L в,

X

X . — C D *

Г A

B

HC x

- Bv

H y C

C

¹ X - = 0,

— C (V“2 — Le2 ) = 0,

ХХ

= 0, Ц - + Ц + — x ^— — у HH

x

y

X3 --- X

C

— х--у l Н х    Н у

+ H — h — L (в- +в4) + V (a4 —

) ^а 3 ) = 0.

Граничные условия 0 <  t <  T при l = 0 имеют вид

d X?  Х^ф

—

dt

H- W ( t ) — Х™ [ 1 + a ( у * ( х , ) '- 1 x

xk

)] = 0,

^ц 1 +

х , ¹

(1)                                           (1)

^L (0, t ) = 0, ц ;; - (0, t ) + Х,2) = 0, H xk

H x k

Ц

+ x ( 0, t ) + X ( ^-) = 0, 2 s z = 0, ^Hx k ^k

grad S V =

^{+ S} ( ^V max

Ц — ^ у (0, t) —Х™ +

H x

+ V min — 2 V ( 0, t ) ) = 0;

при l = 1

(1)         (1)

Х - 1 (1, tbh (1, t ) = 0, dt H xd

-^V ( 1, t ) —ц ( 1, t ) = 0, H_{x d}

Х/ (У (1, t)— x (1, t)) + -2 — Ц- (1, t) = 0, Hxd grad SL = X + Y (Lmax + Lm, — 2 L (1, t)) — Ц4 (1, t) = 0, 2y и = 0.

Начальные условия при t = T , 0 <  l <  1 выглядят так:

Х 1 =Х 2 =Х - = Х 4 = 0, Х < ¹⁾( T ) = 0, Х^( Т ) = 0.

Для вычисления оптимальных управляющих функций V (0, t ) и L (1, t ) применяется итерационный метод, который заключается в следующем:

• 1)    задаются начальные приближения V ⁰(0, t ) и L ⁰(1, t );

• 2)    если известны Vⁿ (0, t ) и Lⁿ (1, t ), то находятся решения прямой и сопряженной задач;

• 3)    полагаем, что V ” ^{+ 1}(0, t ) = V n (0, t ) — T 1 grad S V , L n ^{+ 1}(1, t ) = L ” (1, t ) — T 2 grad S l ;

• 4)    предельные значения L (1, t ) и V (0, t ) дают решение задачи оптимального управления.

Для численного решения краевых задач и задач оптимального управления разработан численный алгоритм с использованием метода центральных разностей и треугольных сеток [1]. В качестве примера приведены результаты расчетов оптимальной управляющей функции L ( l , t ) при оптимизации пускового режима для промышленной колонны К-34 установки серно-кислотного алкилирования изобутана бутиленами (разделяемая многокомпонентная смесь сведена к бинарной). На рис. 2 показано изменение концентрации бутана в сырье (рис. 2, а ), в дефлегматоре (рис. 2, б ), в кубе (рис. 2, в ) при управлении потоком жидкости. Оптимальная управляющая функция L ( l , t ) изображена на рис. 3. При оптимальном управлении выход на заданное значение концентрации целевого продукта происходит быстрее, чем при неоптимальном. Подробное описание установки и экспериментальные значения основных параметров процесса приведены в [5].