Оптимизация проектно-баллистических параметров космического аппарата с солнечной тепловой двигательной установкой при формировании и коррекции низких околоземных орбит

тепловую, которая накапливается в тепловом аккумуляторе (ТА). Перед подачей рабочего тела (водород) в двигатель осуществляется его подогрев в ТА, что повышает удельный импульс тяги двигателя. СТДУ может работать в режиме жидкостного ракетного двигателя (ЖРД) на холодных компонентах топлива (водород-кислород). Характерной особенностью рассматриваемой двигательной системы является ограниченное время работы за одно включение, определяемое рабочей ёмкостью ТА, а также достаточно высокий уровень тяги, что позволяет сократить время манёвра при некотором уменьшении массы полезной нагрузки по сравнению с ЭРД.

В состав СТДУ могут входить следующие основные системы [1]:

• -    система электроснабжения КА, включающая солнечные батареи, аппаратуру преобразования и регулирования;

• -    двигательная установка, включающая маршевый двигатель и тепловой аккумулятор –теп-лообменник с электронагревателем для подогрева водорода перед подачей в двигатель;

• -    система хранения и подачи компонентов топлива.

Основная задача оптимизации в динамике космических аппаратов заключается в доставке полезной нагрузки максимальной массы mпн на заданную орбиту при заданных граничных условиях перелёта, начальной массе КА m0 и времени перелёта Т. Для решения задачи будем использовать проектную модель КА с нерегулируемым двигателем ограниченной мощности с аккумулятором энергии [2]. Предполагается, что ДУ работает в двух режимах: двигатель включён, тяга P и ско- рость истечения рабочего тела с постоянны, происходит разрядка теплового аккумулятора с постоянной мощностью NE ; двигатель выключен – параметры P и с равны нулю, производится зарядка аккумулятора от солнечных батарей с постоянной мощностью NS . Для анализа вводится массовая модель КА, представляемая в виде суммы масс отдельных компонентов аппарата:

mn = m + m + mc + m„ + mA + m + m

0 пн к E S д рт спх ^, где m пн – масса полезной нагрузки, m к – масса элементов конструкции, системы управления и пр., m E – масса ТА, m S – масса СБ, m_д – масса двигателя, m_рт – масса рабочего тела, m_спх – масса системы подачи и хранения рабочего тела.

Массы отдельных компонентов КА принимаются в виде функций:

m k = ^ к ^m 0 , m E = У е^Е 0 , m s = Y s N s ,

m пн = arg max ^m пн И V x = ^V x mm ⁽ У , ^X 0 , x k , ^{T ) ) .} у eY

Для решения динамической задачи используется модель движения в оскулирующих элементах [3]. Вследствие ограниченного времени работы ДУ (до 20 мин.) и относительно небольшой тяги (до 100 Н) приращения элементов орбиты за виток незначительны, а траектория перелёта является многовитковой. Это позволяет упростить систему уравнений движения на основе метода усреднения.

Используя оптимальное управление на витке, полученное в работе [3], модель движения на длительных интервалах времени с учётом второй зональной гармоники в разложении геопотенциала Земли представляется в виде:

m g = У д P , m рт = — T M , m cnx = Р спх m рт , (2)

где E 0 – максимальная накапливаемая аккумулятором энергия (рабочая ёмкость аккумулятора), N S – мощность солнечных батарей, P – тяга двигательной установки, c – эффективная скорость истечения, Т м - моторное время, д к , у _Е , y _s , У ду , Р _спх - соответствующие удельные массовые характеристики. Так как при проектировании КА удельные характеристики аппарата, как правило, известны, то принимаем их постоянными заданными величинами.

Для массы полезной нагрузки можно записать:

dA = 2 dt

dq = 4 dt

A 3 w ₀

д Л

[ 2 ^ — ( л — a ) ],

cos( ^ ) — bk ,

dk a W w₀ . f„ a ) (a V _z , — = 4--sin l q + — I cosl — I sin( ^ ) + bq, dt ]/ д л ( 2 ) (2)

dVx

dt

1 —

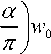
m = mn(1— д ) — у „Б,. — уN„ — пн 0 к E 0 S S

— Уд P — (1 + Рспх )m 0

(    ( v W

1 — expl —II      < c ))

Здесь A – большая полуось орбиты, q и k – компоненты вектора Лапласа, ^ - половина ширины разгонного участка с аргументом широты его центра ^ , a - длительность пассивного участка по аргументу широты, V_x – характеристическая скорость перелёта, д - гравитацион-

ный параметр, b =

В состав вектора оптимизируемых проектных параметров входят тяга ДУ, мощность СБ и рабочая ёмкость ТА: у = ( P , N S , E 0 ) . Если зафиксировать проектные параметры, то максимум полезной нагрузки m пн соответствует минимуму затрат характеристической скорости V x . При этом общая вариационная задача разделяется на динамическую и параметрическую части.

Динамическая задача заключается в поиске оптимального управления, доставляющего минимум затратам характеристической скорости при ограничениях на векторы управления u и состояния x :

A 3,5

A 3,5 ср

, A ср

A 0 ⁺ A k

2 ^,

B = _f ⁽5cos^ ^— 1) , _£ = 2,6333 _Г|

27 Д

км ⁵

_с 2 , i –

наклонение орбиты.

Для поиска оптимальной по быстродействию программы управления воспользуемся принципом максимума Понтрягина. Гамильтониан для системы (4) имеет вид:

— - I +

T = fixe , u opt ^{( t )} = arg min ^V x ⁽ u , ^x 0 , ^X K , ^{T ) x} 0 = fixe , ueU, x e X

Параметрическая часть задачи формализуется следующим образом:

H = 4

0- ^ + sin( E, + -)

V д л          2

cos —X

> +

X ( у _q cos ^ + у _k sin r^

+ b(qy k — kyq )— 1 •

Здесь V A , V _q , V k - сопряжённые множители, уравнения для которых запишутся в виде:

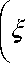
я - a ^

--------I +

2 )

H = 4

. •     . a    a

< + sin( 5 +— )cos— x

2     2

^ +

x ( v _q cos M + V k sin M )

⁺ b ⁽ q V k ^- k V_q ^{) -} 1.

Законы изменения параметров управления определяются из необходимого условия максимума гамильтониана:

tg M opt = — = tg M ⁺ bt ) , M opt = M ⁺ bt . (7) p V q p

Таким образом, оптимальное расположение центра активных участков относительно линии узлов M линейно зависит от времени.

Системы (4) и (5) с полученным управлением (6) и (7) при заданных граничных условиях образуют краевую задачу. Неизвестными являются начальные значения сопряжённых множителей V A 0 , V _q 0 , V k ₀ и время перелёта T . В качестве невязок используются отклонения конечных значений фазовых параметров от требуемых и значение гамильтониана H , которое должно быть равно нулю на оптимальной траектории.

Сформулированная краевая задача может быть решена приближённо. Для первого и третьего этапов уравнения движения (4) интегрируются аналитически:

dH

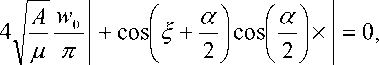
^x( V q cos M ⁺ V k sin ^

dH A W w_n a ) (a ) ----= 4„-sin l 5 + — | cos l — | x d M \ д я ( 2 ) ( 2 )

x ( - v _q sin M + V k cos ^ ) = 0.

A ₀

( 1 - ф! ) 2 , q = e ₀ cos( to ₀ + bt ) - V ln ( 1 - Ф t ) cos( M ₀ + bt ) , (8) k = e ₀ sin( to ₀ + bt ) - v ln ( 1 - Ф t ) sin( M ₀ + bt ) .

После преобразований с учётом ограничения на величину активных участков на витке ( 0 — 5 — я — a ) длительность разгонного участка равна:

k ₀

Здесь e 0 = ^k 0 + q 0 , № 0 = arctg --экс- q ₀

центриситет и аргумент перигея начальной ор-

, _                         A f, a)

биты соответственно, ф = ± w„ —- 1--,

V д l я;

при

при

5 opt

я - a

A V + arcsin , A

a \va\

V V^0 (1 + tg M

— cos ²

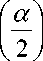
2 q 0

, 1 + sign ( y_A L x

5 opt =----V     ( я - a ) = const

a \va\

V V'o(1 + tg M

> cos

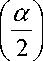
В общем случае программа изменения 5 ( t ) может включать три этапа: первый содержит один разгонный участок на витке: 5 = я - a = const , второй - разгонный и тормозной участки: 0 <  5 <  я - a = var , третий -один тормозной участок: 5 = 0 .

Из условия максимума для параметра M по-

лучаем:

, , sin a

V = ±2-----, знак «плюс» соответствует пер- я - a

вому этапу, знак «минус» – третьему.

Для описания движения КА на втором этапе необходимо получить в явном виде зависимость параметра 5 ( t ) . Система (4) и сопряжённая с ней система (5) допускает интеграл вида:

d (Ay А )    H + 1 - b(qVk - kVq)

—---— =--— = const .

dt 2

Так как для задачи на быстродействие справедливо тождество: H = 0 , то

A V A

A 0 V A 0

^{1 - b (} q 0 V k 0 ^- k V q 0 t

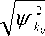
2 a

+ V„ cos — q 0

При этом закон изменения длительности раз-

гонного участка записывается в виде:

^{я - a} ■ /

—-— ⁺ arcsin ⁽ ф , ^- ф 2 t ⁾ ,     (9)

a o V a 0            _ ¹ ~ b ⁽ q 0 V к 0 ~ k V q 0 ⁾

____________        , ^ф2       ____________

а               а

V V k0 ⁺ V q0 cos 2       ² V ^ k 0 + V q0 cos у

3 д acp w0     а где A = 4 —-—-cos — .

у ц л    2

При полученной программе управления параметром L аналитическое решение можно получить только для изменения большой полуоси орбиты:

A =

A

1 _{+ 2} A w 0 f ^{( 1 )} у ц л ф ₂

где f ( 1 ) = ( ф , ~ ф ₂ 1 ) arcsin ( ф , ~ ф ₂ 1 ) ~ ~ ф , arcsin ф , + 7, ~ ( ф , ~ ф 2 1 ) ~ 7, ~ ф , .

Приближённый закон изменения компонентов вектора Лапласа можно получить, полагая, что длительность активных участков на витке мала и большая полуось орбиты меняется незначительно, и можно принять: A ( t ) » Aср = const . Учитывая (9), запишем:

л ~ а

С использованием полученных решений (10) и (11) приближённо-оптимальное управление и траектория перелёта определяются посредством следующего алгоритма:

• 1)    задаются начальные значения коэффициента ф , , начальное значение аргумента широты линии переключения П ₀ и время манёвра T ;

• 2)    с учётом H = 0 вычисляется коэффициент ф : ф 2 = ²_А^ A ⁰-— ^{( 1 +} ф ,^{2 )} ;

у ц л

• 3)    вычисляются начальное и конечное значения длительности разгонного участка:

_е л - а _е л - а /        х

^ 0 =        + ф , , ^ к =        +⁽ ф , ~ ф 2 T ⁾ ;

4) с учётом ограничения на длительность активных участков на витке ( 0 <  ^ <  л ~ а ) определяется время каждого из этапов:

sin l L

= sin у = sin ( ф , ~ ф ₂ 1 ) . При ма-

лых значениях ( у <  5 ⁰ ): sin у = у = ( ф , ~ ф ₂ 1 ) . Тогда искомое решение имеет вид:

L ~ L

0 n      kn ln =              , ф2

A q = e0 cos( ^ + bl)--х 2b

ф , ф ₂l 1 sin ( n ₀ + bl ) ~

sin n ₀ sin bl b

ф 22

2 b

,--у- 1 1 cos ( n ₀ + bl ) ~

I     ф 2 )

cos ^ 0 ^{sin b1}

l b

~ ф-1 ² sin ( n ₀ + b1 )

k = e ₀ sin( ^ + b1 ) + — х 2 b

[ z          cos ^ sin b1

ффl ~ 1 cos(^ + b1) +---------- l                         b

2 b

^, _r 1 ^{1 sin (} ^ 0 + ^{b1 )}~

l    ф2^

~ sin n0 sin b1

l b )

ф 2

+ ^22- 1 ² cos ( n ₀ + b1 )

~

У , (11)

где n = 1..3 - номер этапа, L , L - конечное и kn 0 n начальное значения продолжительности разгонного участка для n-го этапа;

• 5)    по соотношениям (10), (11) последовательно определяются значения фазовых параметров в конце каждого этапа A kn , q kn , k kn , при этом конечное значение параметра для предыдущего этапа является начальным для последующего;

• 6)    определяются отклонения полученных конечных значений параметров орбиты от требуемых, по которым определяется следующее приближение коэффициента ф , , аргумент широты линии переключения П ₀ и времени манёвра T .

Затраты характеристической скорости опре-

I ^а делятся как: V = l ,--I w ₀ T . Полученный ал

" l Л)

горитм может использоваться при незначительных изменениях большой полуоси орбиты A и малых (менее 200) длительностях активных участков на витке.

Результаты могут использоваться для решения краевой задачи в исходной постановке, где начальное приближение сопряжённых множителей определяются как:

W A 0

ф ,

_{2 ф} , ^{b (} q 0 ^1g ^ 0 ~ ^к0^^{д ( cos n} J ²       7, + 1g 2 П ₀ cos а /2

/ A 0 ,

V q 0

Л^О        I   a

---- ⁰ A ° - ------ Sign I cos—

Ф 17 ( 1 ⁺ tg 2 ^ 0 ) cos f    ^{к     2}

V k 0 = V q 0№ .

При наличии пассивных участков на витке полученное управление обеспечивает ограниченную область существования оптимальных перелётов. Границу области можно определить по управлению, состоящему из одного активного участка (разгонного или тормозного) на витке максимальной продолжительности:

^-^ > и sin a

где А = .    lⁿ⁽ A^k / A ⁰ )      , Леи = to k ^-Щ ^- bT

л]e k ^{- 2} e k e 0^{cos АЮ} а ⁺ e 0

– изменение аргумента перигея под действием тяги ДУ. При малых длительностях активных участков ( a ^ Л ) условие (12) определяет множество пересекающихся начальных и конечных орбит. С увеличением активных участков область существования перелётов расширяется и захватывает часть множества непересекающихся орбит. В пределе, при управлении без пассивных участков ( a = 0 ) эта область включает в себя любые замкнутые орбиты.

Если условие (12) не выполняется, то оптимальное управление содержит максимальный разгонный или тормозной участок на витке с переключением аргумента широты центра его приложения на 1800 в определённый момент времени t 1. При этом параметры управления определятся как:

^ =

1 + sign ⁽ A k ^- A 0 ⁾

( л - a ),

V 1 =V 0 + bt , V 2 =V 0 +Л + b (t 1 + t ).

Здесь V о = arctg

~

А k

А ~

Л )

- bT

– аргумент ши-

роты центра активного участка в начальный мо-

ф

к

мент времени, T = — 1

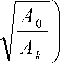
– время манёв-

Затраты характеристической скорости в данном случае зависят только от требуемого изменения большой полуоси орбиты:

Vx = (Л - Л ]Si8" (A1- A0 ’.

Полученные приближённо-оптимальные программы управления позволяют перейти к решению параметрической задачи, заключающейся в определении оптимальных проектных параметров по критерию максимизации массы полезной нагрузки при заданном времени и граничных условиях перелёта.

Задача оптимизации сводится к итерационной процедуре, где оптимизируемым параметром является величина тяги ДУ и в которой каждая итерация включает следующие этапы:

• 1)    Задаются тяга двигательной установки ( P _min <  P <  P _max ), начальная масса КА m 0 , граничные условия x 0 , x k и время перелёта T . Минимальная величина тяги P min ограничивается временем перелёта без выключения ДУ; максимальная P_ = 100Н – техническими ограни- max

чениями.

• 2)    Определяется оптимальное управление и соответствующая траектория перелёта. Рассчитываются затраты характеристической скорости Vx , максимальное значение большой полуоси орбиты Amax и длительность пассивного участка на витке a .

• 3)    Из условия эффективного использования ТА, предполагающего полный его разряд после активного участка максимальной длительности, рассчитывается рабочая ёмкость теплового аккумулятора:

A 3 Pc

E0 =Аta max NE = (л - a)J ^ma^ ~ , \ Д Vt где Аta max - максимальное время работы ДУ; NE -мощность, отводимая от теплового аккумулятора к двигателю.

• 4)    Мощность СБ рассчитывается из условия полного заряда ТА от СБ после цикла работы двигательной установки, включающего в общем случае два активных и два пассивных участка:

ра, V 1 , V ₂ — программы изменения расположения

= Аta max N = Л - a Pc

T,-Аt E a 2v об a max                       T

центров активн ~ ых участков до и после переключения, А k = e_k sin to _k - e ₀ sin ( to ₀ + bT ) , А ~ = e_k cos to _k - e ₀ cos ( to ₀ + bT ) .

Момент переключения t 1 равен:

t ₁

ф

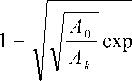
>1 ^А ~ 2 ^{+ А} ~ 2 '

V к                   7

. (14)

где T об - период обращения, V _T - тяговый КПД.

5) Рассчитывается масса полезной нагрузки по соотношению (3).

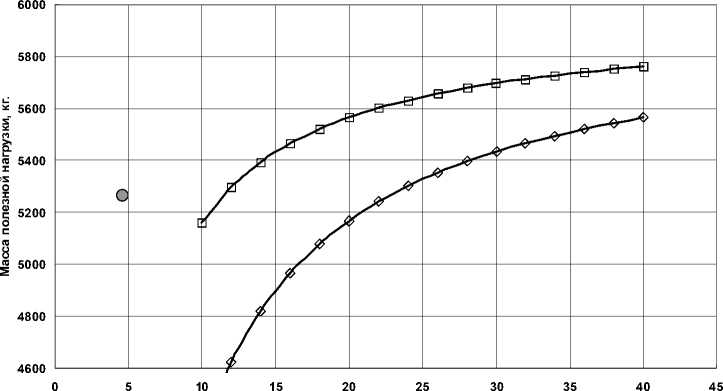
На рис. 1 приведены результаты параметрической оптимизации при формировании рабочей орбиты для исходных данных, представленных в табл. 1, 2. Формирование рабочей ор-

Таблица 1. Параметры КА с СТДУ

Ц	Y e , кг/Мдж	Y s , кг/кВт	Y g , кг/Н	p сп х	П т ,%	m 0 ,кг	P -, н жрд,	c, м/с
0,1	1,18	50 (СТДУ-1) 20 (СТДУ-2)	0,39	0,5	80	7700	234	4532 (режим 1) 7456 (режим 2)

Таблица 2. Параметры орбиты выведения и рабочей орбиты

Орбита выведения			Рабочая орбита
A 0,км	e 0	2 0, град	Ak ,км	e k	® k, град
6578	0,00205	0	7858	0,00248	0

СТДУ-1    СТДУ-2    ЖРД

Время, сут.

Рис. 1. Зависимость массы полезной нагрузки от времени манёвра биты КА осуществляется в два этапа: переход с орбиты выведения на круговую орбиту высотой 300 км на холодных компонентах топлива в режиме ЖРД (режим 1) и многовитковый переход на рабочую орбиту в режиме без дожигания водорода, нагретого в тепловом аккумуляторе (режим 2).

Результаты параметрической оптимизации при коррекции орбиты в режиме работы СТДУ без дожигания водорода приведены на рис. 2 для исходных данных, представленных в табл. 1, 3. Начальная масса КА принималась равной 6570 кг, наклонение орбит при коррек-

ции 69,9 град.

Результаты расчётов показывают, что при определённом увеличении времени межорбитального манёвра СТДУ может обеспечить выведение полезной нагрузки большей массы по сравнению с кислород-водородным ЖРД. Эффективность рассматриваемой двигательной установки в значительной мере определяется энергомассовым совершенством системы электроснабжения. Приведённая методика определения проектных параметров может использоваться на начальных этапах проектирования КА с СТДУ.

Таблица 3. Параметры начальной и конечной орбиты при коррекции

Началь ная орбита			Конечная орбита
A 0,км	e 0	<2 0 , град	Ak , км	e k	2 k , град
6750	0,0149	120	6896	0,0239	0

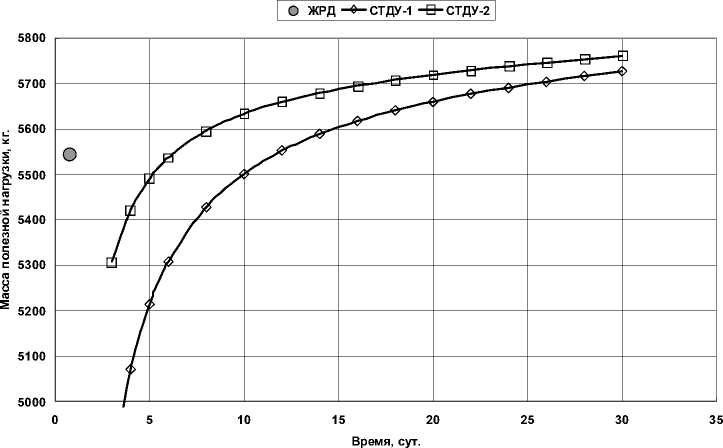
Рис. 2. Зависимость массы полезной нагрузки от времени манёвра