Оптимизация производственной программы выпуска инновационной продукции промышленного предприятия

Инновации, их реализация в значительной мере зависят от многих параметров производственной стадии инновационного процесса. К ним относятся цели, которые стремится достигнуть руководитель промышленной компании, ограничения производственных мощностей и ресурсов, характерные для имеющихся на предприятии технологий производства, использование имеющегося трудового потенциала по максимуму без возможных простоев и значительных избытков, эффективное внедрение в производственную цепочку собственной продукции для изготовления более перспективных товаров и услуг, возможность сделать процесс производства более стабильным и гибким по отношению к возможным рискам и неучтенным факторам. Все эти вопросы указывают на то, что планирование производства инновационной продукции имеет ряд нерешенных проблем, которые в свою очередь обусловливают актуальность проведенного исследования. Целью исследования является разработка математического аппарата, позволяющего оптимизировать производственную программу выпуска инновационной продукции промышленного предприятия. На основе научных работ и трудов Л.В. Канторовича, В.В. Леонтьева и В.В. Новожилова автором спроектирована математическая модель линейного программирования, оптимизирующая выпуск инновационной продукции на промышленном предприятии. Данная модель учитывает различные ограничения, связанные с имеющимися на предприятии ресурсами и мощностями, а также использование собственной продукции при производстве другой. На ее основе разобран пример, в котором оптимизирован выпуск продукции промышленной организации при выборе четырех локальных критериев (максимальная выручка, минимальные производственные затраты, максимальная прибыль и рентабельность продукции). При выборе целевой функции «рентабельность» смоделированная система неравенств теряет свойство линейности (критерий оптимальности - дробь). В связи с этим предложена схема сведения данной задачи к задаче линейного программирования, после чего сформирован подробный ее алгоритм и представлено его применение на наглядном примере. Предложена схема компромиссной программы, учитывающая найденные производственные планы. Дальнейшими направлениями исследования могут быть использование элементов динамического программирования и расчет полученных решений на устойчивость.

Инновации, управление и планирование, производство, линейное программирование, компромисс, промышленные предприятия, оптимизация, эффективность.

Инновационная деятельность является драйвером экономического роста и развития. В своих работах известный австрийский и американский экономист Й.А. Шумпетер [14; 19] указывал на то, что именно инновации, а точнее их беспрерывное производство, позволяют хозяйствующим субъектам заручиться в рыночной среде действенными конкурентными преимуществами. Они могут быть выражены в неповторимости и уникальности оказываемых компаниями услуг и производимых товаров, более качественной и менее затратной технологии производства, снижении рисков при изготовлении продукции и др. [8; 17].

Для активизации инновационной деятельности в регионах РФ необходимо решение проблем, возникающих перед субъектами, непосредственно осуществляющими инновации. В первую очередь к ним относятся промышленные предприятия. Рост их конкурентоспособности благоприятно отразится на социальноэкономическом положении тех территорий, в пределах которых данные предприятия находятся. Речь идет об увеличении притока финансовых средств на территории, создании высокотехнологичных рабочих мест, обеспечении дополнительных налоговых отчислений и т. д.

Инновационная деятельность может быть охарактеризована последовательностью различных стадий и этапов внутри них, которые в своей совокупности описываются в научной литературе как инновационный процесс [3; 13; 20]. Каждой из них соответствует определенный круг специфических задач, которые могут быть решены при помощи различных методов экономико-математического моделирования. Подобная задача присутствует и на стадии производства, и на стадии выпуска инновационной продукции. Ее можно выразить как потребность в обосновании и оптимизации производственной программы предприятия [4; 11]. Правильно сформированный план производства позволяет управляющему предприятием извлечь максимальную выгоду при выборе и достижении конкретных целей, а также оптимальным образом использовать те ресурсы и возможности, которыми он располагает в настоящий момент.

Из вышесказанного следует, что планирование производства является одной из важнейших задач экономической науки. Таким образом, цель данного исследования можно сформулировать как создание математического инструмента, позволяющего оптимизировать программу выпуска инновационной продукции промышленного предприятия.

В ранних работах, опубликованных автором [1; 2], данная задача была смоделирована и решена при условии достижения единой цели методами линейного программирования [5; 16; 18]. В общем виде ее запись выглядит следующим образом:

F_t(X =

^P y t / ^max;          (1.1)

jT

^Cj^xi + C ^ min;        (1.2)

'-1

^(P j - ^Cj)X j ^-C ^ max; (1.3) j^

Z j^1⁽ P j - ^Cj)X j - ^C .   Z j^i C j X j + C

^ max. (1.4)

i = 1,4;

j = 1Д; I E N;

X = {% j };

• (1) –    совокупность целевых индикаторов ( F i ), зависящих от производимой продукции ( X ) (как имеющегося ассортиментного ряда, так и инновационного характера), которых промышленное предприятие стремится достигнуть:

• (1.1)    – функция выручки, значение которой предприниматель стремится увеличить, где x j – объем, производимой продукции (шт. или ед.); p j – цена ед. производимой продукции, по которой промышленное предприятие реализует ее на рынке (ден. ед.);

• (1.2)    – функция затрат на производство, значение которой предприниматель стремится сократить, где c j – переменные затраты ед. производимой продукции (ден. ед.); C – постоянные затраты на производство (ден. ед.);

• (1.3)    – функция прибыли (стремление получить наибольший экономический эффект);

• (1.4)    – функция рентабельности (стремление извлечь максимальную отдачу от используемых единиц затрат).

  ^ a y kX j <  (>)bk;	(2.1)
  ,	(2)
  X j — ^ ' ^ Z X Z + Q j . ^      Z=1 z = j:	(2.2)

• (2) –    совокупность основных ограничений и условий задачи:

• (2.1)    – ограничение или условие на ресурсы (или предписание об их обязательном использовании), которые расходуются во время изготовления товаров промышленными предприятиями (как инновационного характера, так и старого ассортиментного ряда);

• (2.2)    – условие использования одной продукции при изготовлении другой при их одновременном производстве на рассматриваемом предприятии [6; 7; 9].

X ≥ 0 (3)

• (3) –    частные условия. Данное условие характерно для экономических систем и описывает тот факт, что выпуск продукции не может иметь отрицательных значений.

Следует отметить, что данная математическая модель прежде всего направлена на поиск оптимального количества ресурсов, отмеченных в условиях и ограничениях, при достижении ключевых показателей, характеризующих экономическую эффективность хозяйственной деятельности промышленного предприятия при реализации инновационных проектов. Помимо этого планирование производства инновационной продукции имеет ряд других задач, которые организация также пытается решить. Для примера можно отметить следующее: оптимальное размещение производственных мощностей в пространстве цеха; определение временных запасов и возможных простоев в технологической цепочке производства продукции; ликвидация возможного экологического ущерба и др.

Разработанную в статье математическую модель можно иллюстрировать на примере промышленной компании Вологодской области, занимающейся металлообработкой и производством комплектующих и изделий для предприятий, производящих производственные транспортные системы. Исходные данные для нее представлены в табл. 1.

Промышленное предприятие в настоящий момент занимается производством 3 видов продукции ( X = {x 1 , x 2 , x 3 } ): роликов для конвейерных лент и транспортных шестерней. Ролик с износостойкой поверхностью является модификацией продукции старого ассортиментного ряда и по своей сущности является инновационной разработкой. Соответственно для изготовления единицы данного изделия необходим как минимум один обычный ролик ( x 1 ).

Также на основе продаж продукции предприятия в предыдущем году и проводимых им маркетинговых исследований имеется дополнительная информация о спросе на выпускаемую им продукцию. Так, реализация обычных конвейерных роликов (x1) по опыту прошлых лет не встречала каких-либо ограничений, т. е. весь выпуск данной продукции был всегда и полностью реализован на рынке. Более того, на данный момент имеется заказ на 1 тыс. шт. В связи с этим условие их выпуска может быть прописано как – x1 ≥ 1. Новые ролики (x2) в настоящий момент являются неапробированным товаром, но в ходе маркетинговых исследований установлено, что совокупный спрос на них на рынке не должен превышать 25 тыс. штук. Данное условие может быть записано как – x2 ≤ 25. По третьему виду товара (транспортная шестерня – x3) на данный момент уже имеется 2 заказа (по 1000 шт. каждый). А по опыту предыдущих лет было установлено, что не следует производить их в настоящее время в количестве большем, чем 15 тыс. штук. Условие примет вид – 2 ≤ x3 ≤ 15. Математическая модель данной оптимизационной задачи:

F t (^) =

14000(x_! — x , ) + 30000x , + 17000x₃ ^ max;

12000%_! + 12000% , + 14750%₃ + 5000 ^ min;

2000% ! + 4000% , + 2500%₃ — 5000 ^ max;

2000% ! + 4000% , + 2250%₃ — 5000 .12000%_! + 12000% , + 14750%₃ + 5000 ^ max'

i = 1,4;

^r4%_! + 2% , + 2%₃< 48; % ! +% , + 2% 3 < 45;

3%_! + % , + 2%₃< 30;

• - % ! > 1;

% , < 25;

2 < % 3 < 15;

<%_! - 1 > % 2 '

X ≥ 0.

При решении системы уравнений и целевом условии оптимальности – «максимизация рентабельности» симплекс-алгоритм для поиска оптимального значения не подойдет, т. к. функция рентабельности является дробью (нелинейное условие), но тем не менее она может быть сведена к задаче линейного программирования. Для этого функцию (1.4) необходимо преобразовать следующим образом:

Таблица 1. Исходные данные для оптимизации производственной программы (на год) промышленной компании

Ресурсы	Нормы затрат ресурсов при производстве изделия			Запасы ресурсов
	Ролики для конвейерной ленты, тыс. шт. ( x 1 )	Ролик с износостойкой поверхностью, тыс. шт. ( x 2 )	Транспортные шестерни, тыс. шт. ( x 3 )
Экономические показатели
Трудовые, чел.-год	4	2	2	48
Фторопласт, тыс. кг	1	1	2	45
Станочное оборудование, станко-смен	3	1	2	30
Финансовые показатели
Цена за штуку, руб.	14000	30000	12000
Переменные затраты за ед. изделия, руб.	12000	12000	9500
Постоянные затраты, тыс. руб.	5000

S /-i diXi - С

F₄(X) = _vГ^{1 7 7}    ^ max. (7)

S j=1 C j X j + С

В данном примере преобразование уже выполнено и имеет вид (4), функция F 4 . Далее преобразуем знаменатель как:

I

^CjXj ■ С v ■ 12000x₁ + 12000* 2 + 14750x₃ + 5000 = v (8)

и разделим ограничения системы (5) и уравнения (8), а затем введем следующие переменные:

У 1 = ^ У 2 = ^ У з = ^ У о = 1. v v v v

В результате система (4)–(6) при F 4 примет следующий вид:

F₄(Г) = 2000у₁ + 4000у₂ + 2250у_з - 5000у_о ^ max. (10)

'4y i + 2y 2 + 2y₃ - 48у о < 0;

• У 1 + У 2 + 2у₃ - 45у о < 0;

3У 1 + У 2 + 2У з - 30У о < 0;

• У 1 - У о > 0;

• * У 2 -25У о <0;                         (11)

У з - 2У о > 0;

У з ^{- 15} У о < 0;

• У 1 - У 2 - У о > 0;

112000у₁+12000у₂+ 14750у₃ + 5000у_о = 1

Таблица 2. Результаты расчетов по оптимизации программы выпуска промышленного предприятия и достижению локального критерия оптимальности

Целевые критерии опт. Показатели	ZT I s Го s - о ^ = 5 £ о	zr н лэ и S о i S Н 5 с s	1 1 | Б § И ® S н 2 с О	S h В 5 | ^ О- с
Производство продукции, тыс. шт.
Ролики для конвейерной ленты	1	1	6	6
Ролик с износостойкой поверхностью	0	0	5	5
Транспортирные шестерни	13	2	3	2
Использование ресурсов
Трудовые, чел.-год	30	8	40	38
Фторопласт, тыс. кг	27	5	17	15
Станочное оборудование, станко-смен	29	7	29	27
Показатели результативности производственной и коммерческой деятельности промышленного предприятия
Выручка от продаж, тыс. руб.	235000	48000	215000	198000
Производств. затраты, тыс. руб.	208750	46500	181250	166500
Прибыль от реализации, тыс. руб.	26250	1500	33750	31500
Рентабельн. продукции %	12,5749	3,2258	18,6207	18,9189

Y ≥ 0.

Теперь система (10)–(12) является задачей линейного программирования, таким образом, ее решение может быть найдено при помощи симплекс-метода [5].

Определив оптимальные значения y₁, y₂, y₃, y₀ можно рассчитать оптимальные значения переменных из условия (9) для исходной задачи по формулам:

^Х1 =

У 1

—; * 2 = У о

У 2        У з

—; х з = —.

У о        У о

Результаты расчетов алгебраических систем уравнений (4)–(6) и (10)–(12) при единственном критерии оптимальности представлены в табл. 2.

Анализ результатов расчетов оптимизационных программ выпуска продукции промышленным предприятием позволяет сделать следующие выводы:

– максимальная выручка от продажи, которую может получить предприятие при выставленных им ограничениях, равна 235 млн руб. При этом производственные затраты будут составлять 208,75 млн руб., прибыль от реализации – 26,25 млн руб., рентабельность продукции – 12,57%. Будет произведено 1 тыс. роликов для конвейерной ленты и 13 тыс. транспортных шестерней; задействовано 30 человек за год (из 48 возможных); использовано 27 тыс. кг фторопласта из имеющихся складских запасов в 45 тыс. кг; станкопарк в размере 29 ед. оборудования. На основе этого можно отметить, что на предприятии имеется явный избыток фторопласта, который при недостатке складских площадей может быть без каких-либо потерь для выручки устранен в размере 18 тыс. кг. Для производства дополнительных единиц продукции, в первую очередь, необходимо расширение станкопарка;

– минимальные производственные затраты, которые предприятие может понести при выполнении уже имеющихся гарантированных заказов, составляют 46,5 млн руб. При этом будут изготовлены 1 тыс. роликов для конвейерной ленты и 2 тыс. транспортных шестерней. Прибыль от реализации – 1,5 млн руб.; рентабельность продукции – 3,22%;

– максимальная прибыль от реализации, полученная при имеющихся ограничениях, составляет 33,75 млн руб. Производственные затраты составят 181,25 млн руб.; рентабельность продукции – 18,62%. При этом будет изготовлено 6 тыс. обычных роликов; 5 тыс. износостойких и 3 тыс. транспортных шестерней. Будет задействовано 40 рабочих (из 48 имеющихся); 17 тыс. кг фторопласта (складские запасы – 45 тыс. кг); 29 ед. станочного оборудования (из 30 ед. возможного). Как и в случае с максимизацией выручки, имеется явный избыток фторопласта, который составляет 28 тыс. кг. В сравнении с оптимизацией производственной программы по выручке в производственном процессе дополнительно задействованы 10 ед. рабочих. Для производства дополнительной единицы какой-либо продукции в первую очередь необходимы дополнительные единицы оборудования;

– максимальная отдача от производственных затрат (рентабельность продукции) составит 18,92%. При этом производственные затраты составят 166,5 млн руб., а прибыль от реализации – 31,5 млн руб. Будет изготовлено 6 тыс. конвейерных роликов; 5 тыс. роликов с износостойкой поверхностью и 2 тыс. транспортных шестерней. Количество задействованных рабочих в год в размере 38 человек (10 человек свободны); 27 тыс.

кг фторопласта израсходовано; станки и оборудование задействованы в размере 27 штук.

В данном случае имеется возможность производства дополнительной тысячи конвейерных роликов либо транспортных шестерней, т. к. имеющиеся ресурсы предприятия использованы не в полной мере. Но подобное увеличение производства снизит рентабельность продукции в случае с роликами на 0,15 п. п. (значение рентабельности 18,77%); с транспортными шестернями на 0,3 п. п. (значение рентабельности 18,62%). Данная ситуация указывает на то, что производство возможной дополнительной тысячи конвейерных роликов является более рентабельным, чем производство шестерней. Дальнейшее увеличение рентабельности продукции при тех же условиях возможно лишь при увеличении производства инновационной продукции. Производство дополнительной тысячи роликов с износостойкой поверхностью увеличит рентабельность продукции на 0,45 п. п. (значение рентабельности 19,37%), но в имеющихся условиях на предприятии подобная схема невозможна, т. к. не хватает мощностей станкопарка. Дефицит имеющегося у компании оборудования может быть устранен при помощи приобретения новых дополнительных единиц оборудования либо модернизации имеющихся при условии увеличения их производственных мощностей.

Результаты расчетов показывают, что одновременное достижение поставленных локальных целей невозможно за счет выбора какого-то отдельного плана производства продукции. Выход может заключаться в том, чтобы прибегнуть к некоему компромиссному решению. Варианты компромиссов и критерии их формирования подробно разобраны в трудах по теории игр [10; 12; 15]. Примером может служить «минимальное откло- нение от наилучших значений найденных вариантов решения».

Для этого введем следующее условия. Пусть f 1 , f 2 , …, f 3 – веса разных (отличающихся между собой) вариантов производственной программы, полученных при поиске решения задачи с различными целевыми критериями оптимальности. Следует отметить, что s ≤ i . При этом f 1 + f 2 + … + + f s = 1; f 1 ≥ 0, f 2 ≥ 0, ..., f s ≥ 0.

Тогда F 1^max – (F 1¹ f 1 + F 1² f 2 + ... + F 1^s f s ) – отклонение выручки от продаж продукции при компромиссном плане от максимальной (ден. ед.);

(F 2¹ f 1 + F 2² f 2 + ... + F 2^s f s ) – F 1^min – отклонение производственных затрат при компромиссном плане от минимальных (ден. ед.);

F 3^max – (F 3¹ f 1 + F 3² f 2 + ... + F 3^s f s ) – отклонение прибыли от реализации при компромиссном плане от максимальной (ден. ед.);

F₄ ^max – (F₄ ¹ f₁ + F₄ ² f₂ + ... + F₄ ^s f_s ) – отклонение рентабельности продукции при компромиссном плане от максимальной (%).

Если максимальное из рассмотренных отклонений равно e при e ≥ 0 , то выполняются следующие условия:

f F , ^max - (F^f , + F²f₂ + • + TO <  e, I (F^f , + F₂²f₂ + • + TO — F2™ < e, I F₃^max - (F^f , + Fjf 2 + • + F₃^sf_s) < e, (F™^ax - (F^f , + F₄²f 2 + • + F^) < e.

Веса f₁ , f₂ , …, f_s следует установить так, чтобы e было минимальным, т. е. F (f, e) = = e → min.

Таким образом, можно смоделировать следующую задачу линейного программирования:

F (f, e) = e → min(15)

Г^Л + F , ²f 2 + - + F,^f_s + e> TO M ■ M- ■ •■ M e < Г/'^п.

’ F31f1+F32f2 + - + F3sfs + e>F3max,

F^ + F 4 ²f 2 + ■■• + F^ + e — F 4 ^max,

< ^f, ^+f2 ⁺----- + ^fS = ¹

f1 ≥ 0, f2 ≥ 0, ..., fs ≥ 0, e ≥ 0.(17)

Так как те показатели, которые были использованы при составлении математической модели, разнородны, то их необходимо подвергнуть процедуре нормализации. Под ней мы будем понимать приведение каких-либо значений к единому безразмерному масштабу измерения. Для этого обе части неравенств построенной нами системы следует разделить на F 1^max , F 2^min , F 3^max и F 4^max соответственно. Тогда система (15)–(17) примет следующий вид:

F (f, eн) = eн → min.(18)

' F,        F,2             F,н pmax f, + pmax f2 + ^ + ^max fs + e — 1,

F, F2F

² A+ ² f + ^+ ² f p min ^^, p min ²       p min ^s

F,        F32             F3S pmax f, + pmax f2 + ^ + ^max fs + e > 1,

_FLf ^_FLfн^.,

^ max ^f, ⁺ ^ max ^f2 ⁺ ^ ⁺ ^max fs ^{+ e} — 1, .   f , +f 2 +- + f s = 1-

f 1 ≥ 0, f 2 ≥ 0, ..., f s ≥ 0, e ^н ≥ 0. (20)

Найдя веса f₁ , f₂ , …, f_s , можно вычислить значения объемов выпуска продукции промышленного предприятия при найденном компромиссном плане. Для продукции исследуемого в статье предприятия формулы для расчета объемов продукции следующие:

• X , = X^ , + X^ + ••• + X [ f s,

• * 2 = X 2 ^,f , + X 2 ²f 2 + •+ X 2 ^Sf s, (21)

X 3 = X 3 ^,f , + X t ²f 2 + •+ X 3 ^Sf s,

Таким образом, f₁, f₂ ,f₃ ,f₄ – веса найденных 4 вариантов (максимизация выручки, минимизация затрат, максимизация прибыли, максимизация рентабельности) производственной программы. Для них характерно условие неотрицательности и в сумме они равны 1.

235000 – (235000f 1 + 48000f 2 + 215000f 3 + + 198000f 4 ) – отклонение выручки от реализации продукции при компромиссном плане от максимальной (тыс. руб.);

(208750f 1 + 46500f 2 + 181250f 3 + 166500f 4 ) – – 46500 – отклонение минимальных производственных затрат от затрат, которые будут получены при компромиссном плане производства (тыс. руб.);

33750 – (26250f 1 + 1500f 2 + 33750f 3 + + 31500f 4 ) – отклонение максимально возможной прибыли от реализации продукции при компромиссном плане (тыс. руб.);

18,9189 – (12,5749f 1 + 3,2258f 2 + 18,6207f 3 + + 18,9189f 4 ) – отклонение рентабельности продукции при сформированном компромиссном плане от максимально возможной (%).

Если максимальное из выделенных отклонений принять за e (при e ≥ 0 ) и найти такие веса f 1 , f 2 , f 3 , f 4 , чтобы e → min , то можно построить следующую систему неравенств:

F (f, eн) = eн → min.(22)

(235000/ ; + 48000/ , + 215000/ , + 198000/ ; ) + е > 235000, (208750/ ; + 46500/ , + 181250/ , + 166500/ ; ) - е < 46500,

- (26250/; + 1500/, + 33750/, + 31500/;) + е > 33750,

(12,5749/ ; + 3,2258/, + 18,6207/ , + 18,9189/ ; ) + е > 18,9189

/ 1 +/ z +/ з +/ ; = 1.

f1 ≥ 0, f2 ≥ 0, f3 ≥ 0, f4 ≥ 0, e ≥ 0.(24)

Как уже было отмечено выше, показатели «выручка», «производственные затраты», «прибыль» и «рентабельность» являются разнородными, даже несмотря на то что 3 из них рассчитаны в рублях (в абсолютном выражении отклонения по каждому из них могут отличаться в несколько раз, а то и на целые порядки). Нормализовать неравенства можно за счет их деления на соответствующие максимальные (235000 тыс. руб., 33750 тыс. руб. и 18,9189%) или минимальные значения (46500 тыс. руб.). Значения в скобках: выручка, прибыль, рентабельность и затраты, соответственно. Тогда математическая модель линейного программирования примет следующий вид:

F (f, e ^н ) = e ^н → min.                   (25)

-    48000    215000    198000 н

/; + 235000/z + 235000/з + 235000 + е > 1,

208750,   ,

46500 /; + /z +

А +

46500 /;

— ен < 1,

26250    1500        31500 н

33750^{/; +} 33750^{/z + /з +} 33750^{/; + е} > 1, ¹²⁵⁷⁴⁹ / + 3²²⁵⁸ / + ¹⁸⁶²⁰⁷ / , / , _с н >1 18,9189^yi 18,9189^/z 18,9189^{/з /;}         ,

' / 1 ⁺ f z ⁺ Л ⁺ f t = 1.

f 1 ≥ 0, f 2 ≥ 0, f 3 ≥ 0, f 4 ≥ 0, e ^н ≥ 0. (27)

Переменные, полученные в ходе расчетов системы (25)–(27), представлены в табл. 3.

Таблица 3. Рассчитанные веса компромиссного плана при достижении минимального отклонения от максимально возможных результатов производственных программ по заданным критериям оптимальности

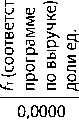
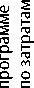
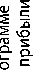
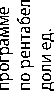
0J S X

0J X о н о

0J о X

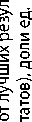
0,7246     0,0000     0,2754     0,7107

Согласно полученному решению минимальное отклонение одновременно для всех наилучших результатов (наибольшая выручка – 235 млн руб.; наименьшие производственные затраты – 46,5 млн руб.; наибольшая прибыль – 33,75 млн руб.; наибольшая рентабельность – 18,9189%) составляет 71,07%. При этом компромиссная оптимизационная программа будет на 72,46% соответствовать плану, построенному по критерию «Минимум производственных затрат», и на 27,54% – по критерию «Максимум рентабельности продукции».

Таким образом, объем производства роликов для конвейерной ленты составит: 1 × 0 + 1 × 0,7246 + 6 × 0 + 6 × 0,2754 ≈ 2 тыс. шт.;

– ролики с износостойкой поверхностью: 0 × 0 + 0 × 0,7246 + 5 × 0 + 5 × 0,2754 ≈1 тыс. шт.;

– транспортные шестерни: 13 × 0 + 2 × × 0,7246 + 3 × 0 + 2 × 0,2754 = 2 тыс. шт.

Полученная полная производственная программа по выпуску продукции промышленного предприятия согласно компромиссному плану в разрезе 4 критериев оптимальности представлена в табл. 4.

Таблица 4. Компромиссный план производственной программы промышленного предприятия

Производство продукции, тыс. шт.
Ролики для конвейерной ленты	2
Ролик с износостойкой поверхностью	1
Транспортные шестерни	2
Объем использованных ресурсов
Трудовые, чел.-год	14
Фторопласт, тыс. кг	7
Станочное оборудование, станко-смен	11
Результативные показатели
Выручка от продаж, тыс. руб.	78000
Производственные затраты, тыс. руб.	70500
Прибыль от реализации, тыс. руб.	7500
Рентабельность продукции, %	10,6383

Используемая в данной работе математическая модель позволяет оптимизировать производственный процесс промышленного предприятия таким образом, чтобы при достижении конкретных финансовых целей можно было в наилучшей мере использовать имеющиеся у него ресурсы. При помощи ее может быть обоснован выпуск инновационной продукции, проиллюстрированы положительные и отрицательные стороны организации ее производства с точки зрения затрат и экономической выгоды по сравнению с прочим ассортиментным рядом.

Также следует отметить, что в статье разобран пример на основе выпуска продукции трех видов при трех производственных ограничениях. В случае с крупной промышленной организацией ассортимент продукции может измеряться десятками и даже сотнями единиц номенклатуры. Аналогично ситуация обстоит и с возможными производственными ограничениями. В связи с этим адекватное и достоверное обоснование производственной программы промышленного предприятия без использования данного математического аппарата попросту является недостижимым. Оптимальное планирование производства позволяет промышленным компаниям достигать наилучших финансовых результатов, что, в свою очередь, запускает новые циклы по созданию инновационной продукции. Для территорий в целом это обеспечивает создание новых рабочих мест, повышение совокупной добавленной стоимости доходов, устойчивое поступление налоговых отчислений в бюджетные фонды. Таким образом, методы линейного программирования могут успешно применяться для планирования и оптимизации производственных программ промышленных предприятий, в структуре которых может присутствовать продукция инновационного характера, а также есть категории товаров, комплектующие для которых производятся непосредственно самой фирмой.