Оптимизация расположения мест крепления приборной панели космического аппарата на основе модального анализа

Проектирование современных космических аппаратов (КА) характеризуется высокой плотностью размещения приборов на панелях для снижения габаритов КА.

Определение мест крепления приборов на панели и мест крепления самой бортовой панели к силовым элементам КА в конечном итоге влияет на диапазон собственных частот КА и его отдельных элементов.

Для выполнения требований по обеспечению несущей способности космических аппаратов требуется его параметрический анализ с целью сравнения полученных характеристик с допускаемым диапазоном, определенным требованиями технического задания.

В процессе проектирования ракетно-космической техники, в целом, и космических аппаратов (КА), в частности, одним из этапов анализа несущей способности конструкции является моделирование её собственных частот и частот её отдельных элементов, например, приборных панелей, с целью обеспечения требований к значениям нижней границы исследуемого частотного диапазона [1–6].

Постановка задачи

Рассмотрим приборную панель, входящую в состав антенны Ка-диапазона в качестве силового элемента, для установки на нее оборудования ретранслятора. Конструкция представляет из себя трехслойный сотопакет, состоящий из двух силовых элементов в виде алюминиевых пластин, между которыми расположены ячейки из алюминиевой фольги гексагональной формы (рис. 1). Общая толщина панели составляет 22 мм.

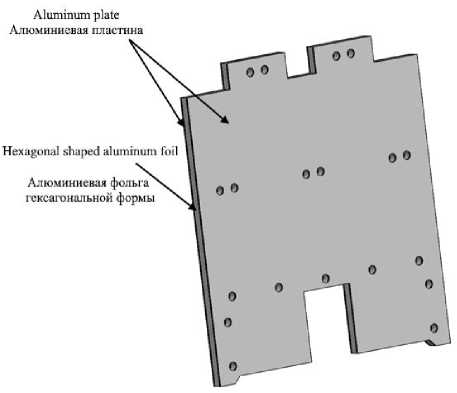
Рис. 1. Модель приборной панели космического аппарата

Fig. 1. Spacecraft instrument panel model

Основные нагрузки панель испытывает при ее транспортировке и на участке выведения КА. Исходя из требований норм прочности к аналогичным приборам, при проектировании необходимо обеспечить минимальную собственную частоту не менее 150 Гц.

Во многих случаях заключение о несущей способности сотовых конструкций принимается в результате обработки результатов натурных испытаний, которые являются достаточно дорогостоящими и трудоемкими. Поэтому оценка параметров конструкции по результатам численного моделирования, имитирующего условия натурных испытаний, является актуальной задачей для снижения себестоимости процесса проектирования [7].

Для проведения параметрического анализа приборной панели КА нами были определены следующие задачи:

• -    сформировать конечно-элементную модель приборной панели;

• -    провести её модальный анализ и сравнить диапазон собственных частот с допустимым нижним значением;

• -    оценить несущую способность приборной панели от действия квазистатических нагрузок;

• -    изучить влияние расположения точек крепления панели на изменение диапазона собственных частот панели и повышение её несущей способности.

Конечно-элементная дискретизация поверхности приборной панели представлена на рис. 2.

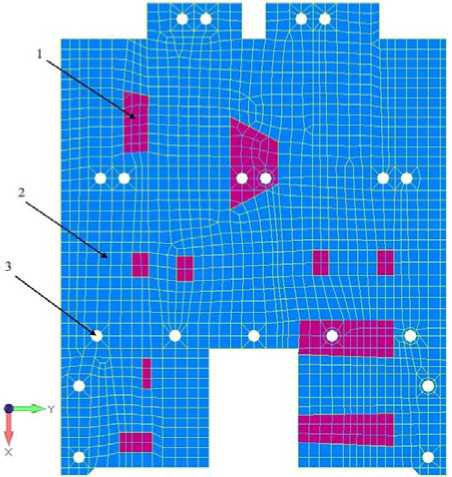
Рис. 2. Конечно-элементная дискретизация приборной панели КА: 1 – расположение приборов; 2 – точки крепления приборной панели – интерфейсные точки; 3 – приборная панель

Fig. 2. Creating a finite element dashboard model:

1 – device location; 2 – dashboard mounting points-interface points;

3 –dashboard

В табл. 1 а и 1 б приведены физико-механические характеристики материалов, применяемых в приборной панели.

Физико-механические свойства алюминиевой пластины

Таблица 1а

Марка материала	Модуль упругости, ГПа	Предел прочности, МПа	Предел текучести, МПа
Алюминиевая пластина В95	74	520	440

Физико-механические свойства сотового заполнителя

Таблица 1б

Материал	Предел прочности, МПА			Модуль упругости при сдвиге, МПА		Объемная масса, кг/м3
	При сжатии	При сдвиге		Параллельно клеевым полосам	Перпендикулярно клеевым полосам
		Параллельно клеевым полосам	Перпендикулярно клеевым полосам
Алюминиевый сотовый заполнитель 5056-2,6-23п	1,177	0,981	0,588	147,1	78,5	40,0

В качестве расчетных нагрузок нами были приняты массовые силы от веса панели с приборами при перегрузке n = 20g, приложенные попеременно в направлении трех координатных осей, согласно регламенту требований к таким конструкциям.

Параметрический анализ конструкции панели позволяет решить задачи определения напряженно-деформированного состояния в ее основных конструктивных элементах, усилий и деформаций в характерных узлах, анализа собственных форм и частот панели в целом и ее отдельных частей в частности.

Расчетная модель приборной панели

При составлении расчетной модели нами были приняты следующие допущения:

• –    все материалы элементов конструкции считаются сплошными и однородными;

• –    металлические сплавы принимаем изотропными и линейно-упругими материалами;

• –    деформации в точках конструкции считаются малыми (геометрически линейная система) и жесткость конструкции не меняется в процессе нагружения;

• –    толщины и размеры деталей соответствуют номинальному значению (введен коэффициент безопасности на отклонения размеров от номинальных).

В конечно-элементной модели (КЭМ) реальный объект заменяется дискретной моделью, которая представляет собой совокупность узлов и связанных с ними конечных элементов с заданными свойствами.

КЭМ приборной панели, разработанная с учетом принятых допущений, представлена на рис. 2. Свойства материалов КЭМ заданы в соответствии с табл. 1 а и 1 б . В качестве граничных условий была принята жесткая заделка по девятнадцати интерфейсным точкам (рис. 2).

Готовая КЭМ для расчета панели была сформирована с использованием программного комплекса FEMAP [8–10]. Крепление приборов в интерфейсных точках было реализовано с помощью жесткой связи – элемент Rigid, масса приборов распределена по элементам панели. Сама приборная панель составлена из конечных элементов типа laminate (рис. 2).

Для аналитического расчета собственных частот рассмотрим классические уравнения колебаний пластин [11; 12]. При пренебрежении демпфированием дифференциальное уравнение движения свободных колебаний системы с n степеням свободы описывается уравнением [11; 12]:

[ M ]{ и } + [ K ]{ и } = 0,                                       (1)

где [ K] и [ M] - матрицы жесткости и масс; { u } и { и } - векторы ускорений и перемещений в узлах КЭМ.

Уравнение (1) имеет вещественное периодическое решение вида

{ и } = { u ₀ } cos ю t .                                              (2)

При выполнении условия

( [ K ] -® ² [ M ] ) { u 0 } = 0.                                    (3)

Задача расчета собственных форм и частот колебаний сводится к задаче о собственных значениях rek и векторах {u0}k, которые обращают в ноль определитель det |[ K ] re' [ M ]| = 0.                                         (4)

Подобная задача для многослойных пластины из композиционных материалов и прямоугольных ортотропных пластин ранее уже была решена [13; 14]. Процесс деформирования прописан уравнениями нелинейной теории пластин, полученная система уравнений решена с помощью метода Галеркина. Полученная формула позволяет определить перемещения, деформации и напряжения в заданных точках конструкции. Кроме того, была выведена формула для определения собственных частот пластины.

Воспользуемся аналитическими формулами, выведенными в работах [13; 14], для вычисления собственных частот пластины.

Для верификации результатов, полученных с помощью аналитических формул, решим задачу модального анализа неоднородной изотропной пластины с помощью метода конечных элементов. Определим собственные частоты конструкции, используя пакет MSC Nastran [8; 10]. Значения собственных частот, найденные с помощью метода конечных элементов, сравним со значениями, полученными аналитически. Максимальная относительная погрешность между этими перемещениями не превышает 5 %, что подтверждает корректность принятой нами конечно-элементной модели приборной панели.

Результаты модального анализа конечно-элементной модели пластины приведены в табл. 2. Первое значение собственной частоты колебаний составило 76,13 Гц.

Таблица 2

Результаты модального анализа исходной панели

Номер тона	Частота, Гц	Эффективная масса, %
		X	Y	Z	RX	RY	RZ
1	76,13	—	—	15,29	—	6,16	—
2	173,00	—	—	5,10	—	2,03	—
3	189,10	—	—	9,53	—	7,36	—
5	276,34	—	—	2,12	—	—	—
6	282,97	—	—	6,98	—	3,82	—
7	291,93	—	—	1,04	—	—	—
8	297,15	—	—	24,67	—	16,26	—
9	336,53	9,79	10,18	—	10,06	4,26	8,61
Итого		9,79	10,18	68,71	10,82	43,40	8,61

Расчет на прочность от квазистатического нагружения

Для проверки несущей способности панели нами был проведен расчет напряженно-деформированного состояния конструкции от массовых сил при перегрузке n = 20g приложенных в направлении трех координатных осей. Ниже приведены результаты квазистатического расчета, в которых отражены максимальные напряжения в приборной панели и её запас прочности (табл. 3 и 4).

При этом запас прочности для обшивочного материала был определен по формуле (5):

[a] n= , ^экв

где [σ] – допускаемое напряжение.

Запас прочности для сотового заполнителя определялся по формуле (6):

' т~-^ kmsi xz yz

'

- 1 - 100 %,

где т xz , т yz - расчетные напряжения сдвига в плоскости, параллельной клеевым полосам, и плоскости, перпендикулярной клеевым полосам, соответственно, Па; т l , т w - предел прочности по сдвигу в плоскости, параллельной клеевым полосам, и плоскости, перпендикулярной клеевым полосам, соответственно, Па [15].

Таблица 3

Результаты квазистатического расчета обшивочного материала до модификации панели

Материал	σ	η
Алюминиевая пластина	216	1,65

Таблица 4

Результаты квазистатического расчета сотового заполнителя до модификации панели

Материал	τ yz	τ xz	η
Алюминиевый сотовый заполнитель	0,29	0,18	2,63

Примечание. η – коэффициент запаса; σ – нормальные напряжения; τ – касательные напряжения.

Распределение напряжений по поверхности приборной панели показано на рис. 3.

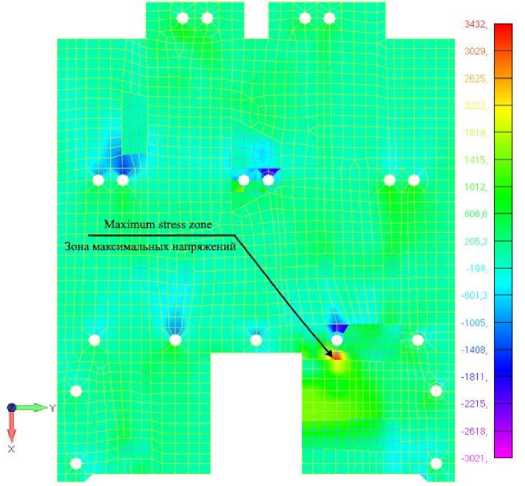
Рис. 3. Зона максимальных напряжений до модификации расположения точек крепления панели

Fig. 3. Maximum stress zone before modifying the location of the panel mounting points

Результаты расчета показали допустимый запас прочности, что подтверждает обеспечение несущей способности панели в процессе её эксплуатации.

Конструктивные изменения приборной панели

Поскольку минимальное значение собственной частоты колебаний панели с базовым расположением кронштейнов не соответствует необходимым требованиям по частотам и, следовательно, предельным величинам линейных перемещений, было решено изменить первоначальную конфигурацию панели, скорректировав места расположения интерфейсных точек крепления. Анализ форм колебаний панели (рис. 4) по зонам с максимальными линейными отклонениями позволил нам определить места корректировки интерфейсных точек. Изменив расположение точек для крепления панели к корпусу КА (рис. 5), нам удалось добиться повышения собственной частоты колебаний всей конструкции.

В табл. 5 приведены значения параметров модального анализа панели с измененными точками расположения кронштейнов крепления. Минимальная собственная частота колебаний модифицированной приборной панели составила 212,96 Гц.

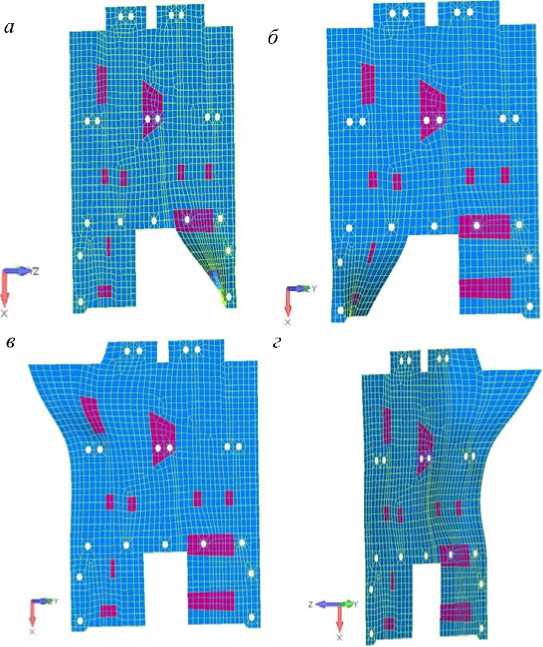
Рис. 4. Основные формы колебаний панели до модификации: а – первая; б – вторая; в – третья; г – пятая

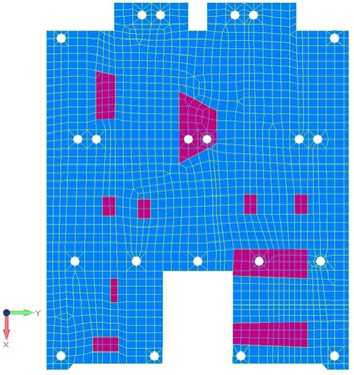
Рис. 5. Измененная конфигурация приборной панели

Fig. 4. Basic panel forms of oscillation before modification: а – first; b – second; c – third; d – fifth

Fig. 5. Modified dashboard configuration

На рис. 6 приведена первая форма колебаний модифицированной панели с измененными интерфейсными точками установки кронштейнов.

Таблица 5

Номер тона	Частота, Гц	Эффективная масса, %
		X	Y	Z	RX	RY	RZ
1	212,96	—	—	18,21	—	7,43	—
2	238,35	—	—	12,58	—	9,62	—
3	282,14	—	—	19,43	—	11,19	—
5	313,60	—	—	8,85	—	6,08	—
6	322,80	—	—	8,63	—	3,73	—
7	373,70	—	—	2,73	—	1,23	—
8	399,98	—	—	3,44	—	1,68	—
9	421,65	—	—	1,44	—	—	—
10	448,78	7,73	17,01	—	16,81	3,37	14,31
Итого		7,73	17,01	75,72	17,66	45,22	14,31

Fig. 6. The first form of oscillation of the modified panel

Расчет на прочность модифицированной панели от квазистатического нагружения

Проведенный квазистатический расчет конструкции приборной панели (табл. 6, 7) подтверждает наличие требуемого запаса прочности для её безопасной эксплуатации, что подтверждается картиной распределения напряжений (рис. 7).

Таблица 6

Результаты квазистатического расчета обшивочного материала после модификации панели

Материал	σ	η
Алюминиевая пластина	65	5,44

Таблица 7

Результаты квазистатического расчета сотового заполнителя после модификации панели

Материал	τ yz	τ xz	η
Алюминиевый сотовый заполнитель	0,05	0,16	6,65

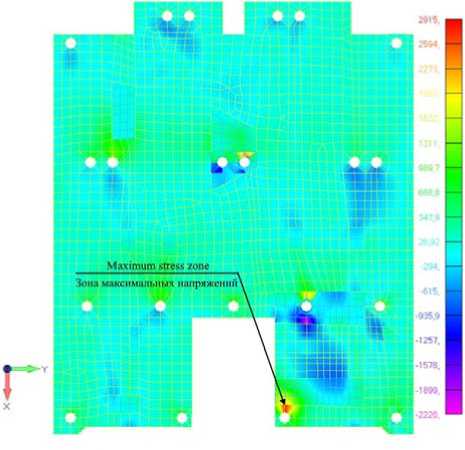
Рис. 7. Зона максимальных напряжений после модификации расположения креплений панели

Fig. 7. Maximum stress zone after modification of the panel mounting configuration

Заключение

Проведенный нами модальный анализ позволил модифицировать приборную панель КА и привести ее в соответствие с требованиями по собственным частотам колебаний. С помощью рационального перераспределения интерфейсных точек удалось достичь увеличения нижней границы частот собственных колебаний до 212, 96 Гц без увеличения массы конструкции. Ква-зистатический анализ подтвердил наличие достаточного запаса прочности у приборной панели и возможность расположения на ней дополнительных приборов за счет увеличения запаса прочности после изменения мест расположения точек крепления панели к корпусу КА. Предлагаемый подход к проведению модального анализа элементов конструкции может быть использован в инженерных расчетах при проектировании КА.