Оптимизация распределенных информационно-измерительных систем
Автор: Демиденко Н.Д., Кулагина Л.В.
Журнал: Журнал Сибирского федерального университета. Серия: Техника и технологии @technologies-sfu
Статья в выпуске: 8 т.13, 2020 года.
Бесплатный доступ
Рассмотрена задача оптимизации информационно-измерительной системы для управления объектами с распределенными параметрами. Сформулирована задача оптимального управления с использованием функций распределенного контроля (измерения). Получены необходимые условия оптимальности. На основе этих условий построен численный алгоритм вычисления оптимальных функций распределенного контроля. Проведены численные эксперименты.
Математическое моделирование, системы оптимального управления, функции распределенного контроля
Короткий адрес: https://sciup.org/146281621
IDR: 146281621 | УДК: 517.977.56 | DOI: 10.17516/1999-494X-0275
Текст научной статьи Оптимизация распределенных информационно-измерительных систем
Цитирование: Демиденко, Н.Д. Оптимизация распределенных информационно-измерительных систем / Н.Д. Демиденко, Л.В. Кулагина // Журн. Сиб. федер. ун-та. Техника и технологии, 2020. 13(8). С. 923–932. DOI: 10.17516/1999-494X-0275
Система распределенного контроля, содержащая п линейных точечных датчиков, характеризуется вектором распределенного контроля: у = ( х 1 , ... , х п ; д 1 , - — , дп ), где x i — координаты установки датчиков; д 1 , — , дп - коэффициенты усиления датчиков. Теоретически, если датчики устанавливаются во всех точках области D , мы приходим к понятию системы непрерывно-распределенного контроля, которая характеризуется весовой функцией распределенного контроля д ( х ) с Q .
Аналогичным будет представление о системе распределенного воздействия как о совокупности устройств, установленных в различных точках управляемого объекта с распределенными параметрами и предназначенных для изменения состояния объекта.
Система распределенного воздействия вместе с управляющим устройством (которое получает информацию от системы распределенного контроля) образует систему распределенного управления. При увеличении объема поступающей информации необходимо освободить человека-оператора как слабое звено в системе. Это обусловлено не только возрастанием непосильной нагрузки на человека, но и субъективностью суждений оператора при оценке состояния процесса. Необходима строго обоснованная автоматическая оценка поступающей информации о состоянии процесса, а также рациональная организация самой системы контроля.
Достаточно общая задача состоит в том, что требуется найти оптимальную оценку состояния данного процесса для формирования регулирующих воздействий по каждому каналу по данным распределенного контроля. Найденная оптимальная оценка состояния процесса дает решение рациональной организации системы контроля для получения необходимой информации. В частности, может быть полезна идея оптимизации систем управления типовыми технологическими процессами, состоящая в следующем.
Предполагается, что используемый класс управляющих устройств ограничен и большей частью состоит из типовых регуляторов. Решается задача установления наиболее рационального способа контроля управляемого объекта, обеспечивающего при данных условиях наилучшее управление им. Другими словами, оптимизируется процесс управления, прежде всего за счет удачного выбора критерия состояния процесса и использования распределенного контроля.
В наиболее простом случае эта задача приводит к нахождению той или иной весовой функции распределенного контроля. Тогда реализация систем управления сводится к установке на объекте некоторого количества датчиков, сигналы которых определенным образом усредняются и поступают на управляющее устройство. Условная схема системы изображена на рис. 1.
В более сложном случае при управлении учитывается изменение не только самих функций, характеризующих процесс в объекте, но и их производных (скоростей) по временнóй и пространственной координате.
Результаты исследований [1-3] показали, что применение данного метода дает возможность повысить качество управления процессов при использовании сравнительно простых технических средств. Таким образом, с помощью рациональной организации распределенного контроля могут решаться важные задачи оптимизации систем регулирования.
Постановка задачи
Мы рассмотрим простейшие математические постановки задач оптимального сбора информации в замкнутых автоматических системах, содержащих объекты с распределенными
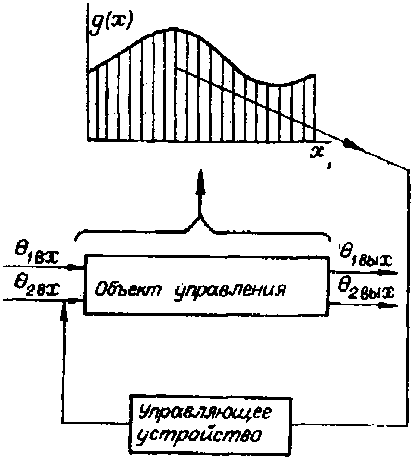
Рис. 1. Принципиальная схема использования непрерывно-распределенного контроля
Fig. 1. Schematic diagram of continuously distributed control application параметрами. В системах управления технологическими объектами большинство используемых датчиков по своим характеристикам близко к точечным. Тем не менее полезно начать обсуждение вопросов оптимального сбора информации в системах с распределенными параметрами системы, содержащей распределенный датчик.
Способ обработки информации в такой системе простейший, он заключается в интегрировании с некоторым весом функции состояния объекта по всей области пространства, в которой распределен процесс.
Такая постановка оправдана, во-первых, тем, что в некоторых производствах все же используют датчики с распределенными параметрами (например, при производстве стеклопластиков применяют датчик, распределенный по длине объекта [4]). Bo-вторых, она позволяет выяснить предельные возможности улучшения качества управляемых систем за счет рационального сбора информации, поскольку оценка состояния объекта, сформулированная указанным способом, является наиболее общей в классе линейных безынерционных оценок. В-третьих, имея весовую функцию распределенного контроля, можно поставить задачу об «аппроксимации» этой функции некоторой решетчатой функцией, что соответствует замене распределенного датчика конечным числом точечных датчиков. Подобный путь хотя в принципе и возможен, однако не кратчайший.
Постановка задач об отыскании оптимальных весовых функций распределенного контроля представляет и методический интерес, поскольку обнаруживается общность задач оптимального сбора информации с задачами оптимального управления пространственно-распределенными объектами. Поэтому для решения задач оптимального контроля можно использовать математический аппарат теории оптимального управления объектами с распределенными параметрами.
Управляемый процесс описывается следующей системой дифференциальных уравнений:
50/x, t) 50/x, t) dt + Эх
Э02(х, t) d02(x,t)
------to?--------- dt dx
= k^^x, t) - 02(х, О) + №>(1)
= k2(02(x, t) - Q^x, t)),
где f ( x)w ( t ) - внешнее воздействие с управляемой функцией w ( t ); w, (i = 1, 2) - скорость течения взаимодействующих сред; k i , (i = 1, 2 ) - теплофизические параметры; ai=^ - обобщенные параметры объекта.
Дополним систему (1) начальными
61(^011=0 = 6ito, 02toOlt = O = 02 to
и граничными условиями
0/0, t) = 0iB1(t), 02С1/ 0 = ЭгвгСО-
Система (1)-(3) представляет собой простейшую математическую модель управляемого процесса с распределенными параметрами, например динамику теплообменных аппаратов с тонкими стенками.
Будем полагать целью системы управления объектов (1)–(3) минимизацию функционала качества
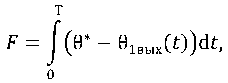
где 9 * - заданное значение управляемого параметра.
Переходный процесс в регулируемой среде в оригиналах можно представить следующей формулой:
J G11(x,t,T)01BX(T)dT + о
di,
о где G 11, G12, G12 - импульсные переходные функции, представляющие собой реакцию объекта на воздействие в виде δ-функции по соответствующим каналам воздействий. Оба регулятора определяются функциями
v
J it/^/ipZ/dT, w(t) = -j it2(t,T)(p2(T)dT, о о
где u 1(t, т), u2(t, т) - ядра, которые считаются заданными; ф1(t) и ф2(t) - сигналы, поступающие на регуляторы и выражающиеся следующими соотношениями:
Ставится задача нахождения таких функций распределенного контроля
д
1
(
X)
и
д
2(
x),
которые минимизируют функционал качества (4).
Подставим (6) в 9
1
(
x,t
) и получим
где введены следующие векторные функции:
м^х,
сЛтА) = е^т)
м^сЛтА) = е^т)
J
G12(x, ^и^.т)^,
О
J
G12(x,
t,r|)ii2(r|,T)dr|.
О
Поварьируем оптимальную весовую вектор-функцию
g
(
x
):
д№ = to to, U, x e [0,11/6, x e 6,
где
g
(
x
) и
G
e
Q; 5 - сколь угодно малый отрезок внутри [0, 1], длина которого равна е. Функционал качества
F
получит следующее значение:
т
Р(Ю = 1^*-
(е^СО + Д01вых(О))2 dt = о
т = У ((0* - 01вь,х(О)2 - 2(0* - 01вых(О)Д01вв1х(О) dt. О После несложных тождественных преобразований найдем Д01вых(О = -Е ((6 - до. XМ(1, г, 5,Т, 0J dT + + /^ £ Г(1, t, 5, т) /от м (^, Т, n, ejdndTd^, где резольвента Г(x, t, ξ, τ) удовлетворяет уравнению
Подставляя теперь Д01вых(
t
) в выражение для
F(д),
получим
Р(Ю = F(g)
- 2E(n(^',G) - П^дЮ)
где Далее имеем AF = F(g) - F(g) = -2е(П(^, G) - П(^.дО) > 0, откуда
Поскольку
g
(
x) -
оптимальная вектор-функция, a
G
- произвольный элемент Q, то последнее условие означает, что для оптимальности
g
(
x
) необходимо, чтобы функция П(^,
g
©) достигала максимума при любом фиксированном ξ
.
Если Q определяют неравенства |
g
i
(
x
)| < 1,
i =
1, 2, получаем
Результаты численного моделирования, их обсуждение и выводы Рассмотрим результаты численного анализа переходных процессов и весовых функций распределенного измерения в объектах с распределенными параметрами в замкнутой системе регулирования при распределенном управляющем воздействии. Эти результаты сравнивают с кривыми переходных процессов и весовыми функциями распределенного измерения без распределенного управления, когда управление осуществляли только за счет изменения граничных условий (при регулирующем воздействии, поступающем только на вход объекта).
Весовые функции
g
1
(
x
) и
g
2(
x)
находили из полученных необходимых условий оптимальности методом последовательных приближений.
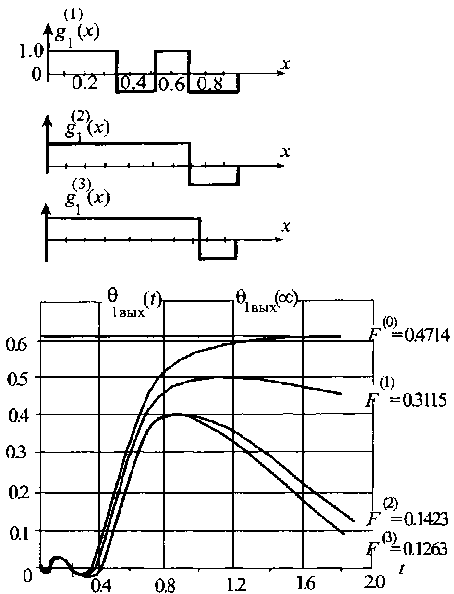
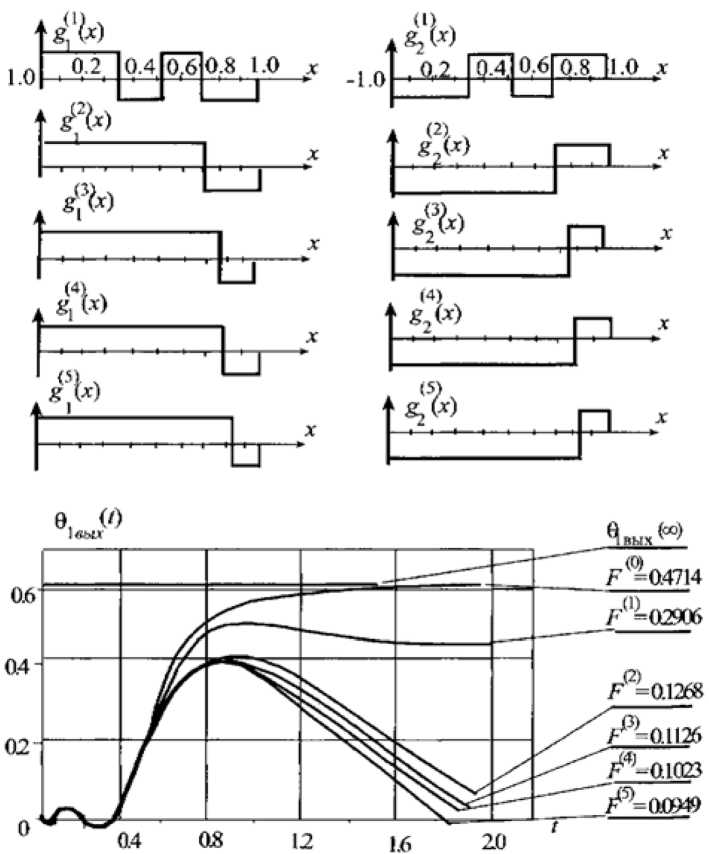
На рис. 2 и 3 представлены кривые переходных процессов и весовых функций, получающихся на каждой итерации. Анализ переходных процессов проводили для параметров технологических аппаратов а
1
с [0, 10] и а2 е [0, 10]. Время регулирования
Т =
2, 0. Как показали расчеты, для устойчивых переходных процессов итеративный процесс довольно быстро сходится. В пределах требуемой точности обычно делают 5–6 итераций. Кривые, обозначенные
Рис. 2. Кривые регулирования в одноконтурной системе [5] Fig. 2. Control curves in a single-loop system [5]
F
(0)
, соответствуют переходному процессу в разомкнутой системе регулирования. При этом новое установившееся значение выходной величины совпадает с полученными стационарными значениями по методу инерционности.
Проведенные расчеты показывают, что качество регулирования при распределенном управляющем воздействии повышается. Так, для параметров а1 = 1, a2 = 2 (см. рис. 2) показатель качества
F
опт
= 0,1263 без распределенного воздействия, а при распределенном управлении (рис. 3) с подачей управляющего воздействия в точку аппарата с координатой
x
;
= 0,7
F
опт
= 0,0949. При этом показатель качества улучшился примерно на 20 %.
Ниже приведем описание блок-схемы программы расчета оптимальных весовых функций, соответствующих функций переходного процесса и функционала качества системы регулирования. Основные этапы вычислительного алгоритма:
1) задается начальное приближение весовых функций распределенного контроля
д®
(Z),
i =
1, 2, ^ ,
п
;
2) вычисляются значения функций 91(0,
t),
91(1,
t
), А91(0,
t
), А91(1,
t
) в замкнутой системе регулирования;
3) по формуле (4) рассчитывается значение функционала
F
;
4) по формулам (7) определяются новые значения функций
g
i
(
l
);
5) уточняются функции
g
i
(l
),
i
= 1, 2, ...,
п,
начиная с пункта 2, до совпадения с заданной точностью двух последовательных приближений.
Рис. 3. Кривые регулирования в двухконтурной системе [5] Fig. 3. Control curves in dual-system [5] Исследования показывают, что алгоритм достаточно быстро сходится к искомым решениям. Благодарности / Acknowledgments Исследование выполнено при финансовой поддержке РФФИ и Правительства Красноярского края в рамках научных проектов № 18-48-242001 «Теплофизические и гидродинамические особенности кинетики смесеобразования при иммобилизации радиоактивных отходов в цементную матрицу с использованием эффектов кавитации» и 18-41-242004 «Теоретические основы кондиционирования вод питьевого назначения на базе эффектов гидродинамической кавитации».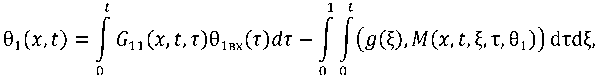
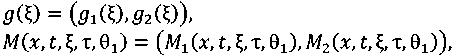
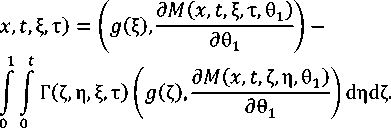
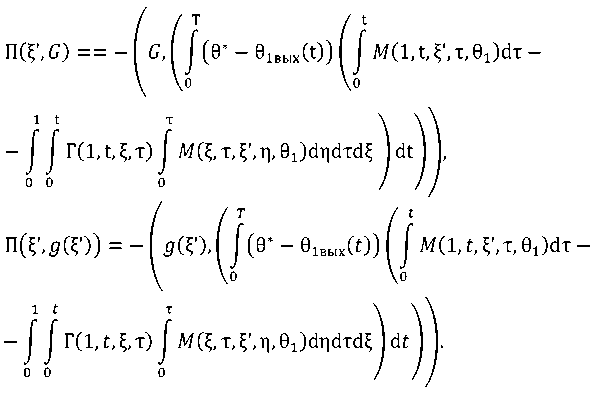
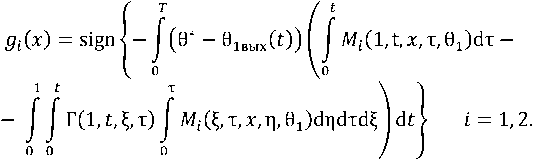
Список литературы Оптимизация распределенных информационно-измерительных систем
- Демиденко Н.Д. Моделирование и оптимизация тепломассообменных процессов в химической технологии. М.: Наука, 1991. 240 с.
- Демиденко Н.Д. Управляемые распределенные системы. Новосибирск: Наука, 1999. 393 с.
- Демиденко Н.Д., Кулагин В.А., Шокин Ю.И. Моделирование и вычислительные технологии распределенных систем. Новосибирск: Наука, 2012. 424 с.
- Бугров А.В., Дудкин Н.И., Масленников И.М. Об управлении химико-технологическими объектами с пространственно распределенными параметрами с использованием емкостных измерительных преобразователей. Автоматизация химических производств. М.: НИИТЭХИМ, 1973. Вып. 1. С. 34-47.
- Demidenko N.D., Kulagina L.V., Pyanykh A.A. Optimal control of systems with distributed parameters, J. Sib. Fed. Univ. Eng. technol. 2019, 12(8), 903-915. 10.17516/1999-494X-0190 (in Russian). DOI: 10.17516/1999-494X-0190(inRussian)


