Оптимизация размеров стального гнутого швеллера

Введение. Прокатные и гнутые швеллеры (рис. 1) используются в различных видах стальных конструкций: фермах, колоннах, связях, мостах и др. Также широко применяются швеллеры в качестве прогонов покрытия (рис. 2). Сравнение весовых характеристик швеллеров показывает, что при равном моменте сопротивления расход стали на гнутые швеллеры несколько меньше, чем на прокатные. Следовательно, их применение в конструкциях является экономически более целесообразным.

А) Б)

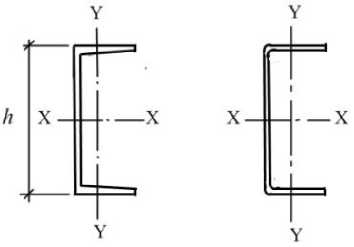
Рисунок 1 – Швеллеры стальные горячекатаные (А) по ГОСТ 8240-97 и швеллеры стальные гнутые равнополочные (Б) по ГОСТ 8278-83

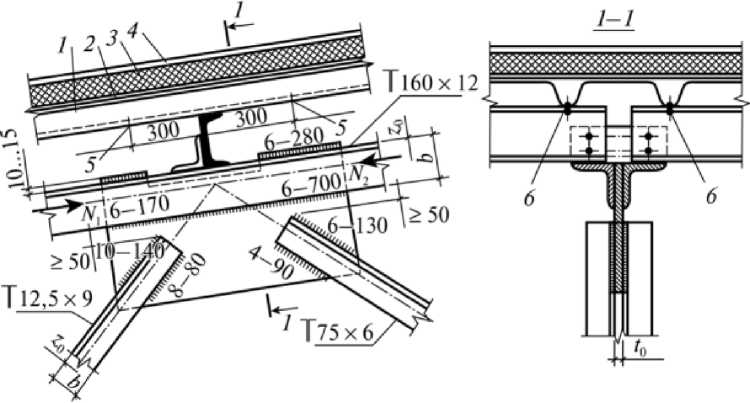
Рисунок 2 – Опирание стального прогона на верхний пояс фермы покрытия

Стальные гнутые равнополочные швеллеры изготовляют на профилегибочных станах из полосовой холоднокатаной и горячекатаной стали различного качества толщиной от 2 до 9 мм. Высота швеллеров может изменяться от 25 до 160мм, длина – от 3 до 12м. Как показало рассмотрение ГОСТ 8278-83 на гнутые стальные швеллеры и технической литературы [1-4], размеры формируемых из исходной полосы гнутых профилей не всегда соответствуют максимально возможному моменту сопротивления сечения, от которого зависит несущая способность изгибаемого элемента.

В связи с этим цель исследования предусматривала определение в общем виде зависимости между параметрами прогона из гнутого швеллера и соответствующим им максимальному моменту сопротивления поперечного сечения.

Результаты исследования. Известны различные методы оптимизации стальных конструкций по различным критериям: минимум массы, стоимости и др.[5-7]. Для достижения поставленной цели признано целесообразным использование аналитического метода.

При подборе сечения однопролётных стальных гнутых прогонов швеллерного типа проверка их прочности и прогиба выполняется соответственно по формулам (1) и (2)

о = М/ W_nc (1)

f = 5 /384 < (/) (2)

• ¹    EWh/ 2 ^{v У X} '

В оба уравнения входит момент сопротивления сечения W и, как следует из формул, чем больше его значение, тем в элементе будут меньше напряжения о и его прогиб f . Следовательно, для снижения расхода стали на прогон размеры его стенки и полок должны соответствовать максимальному моменту сопротивления сечения W.

Задачу оптимизации размеров гнутого швеллера можно сформулировать следующим образом: из полосы шириной S , толщиной t , площадью поперечного сечения A изготовить (согнуть) швеллер, имеющий максимальный момент сопротивления W Х . Определить соответствующие значения высоты швеллера h и ширины полок b (рис. 3).

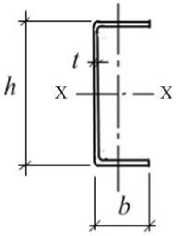
Рисунок 3 – Параметры оптимизируемого сечения швеллера

Установим, при каких условиях момент сопротивления швеллера будет максимальным. Осевой момент сопротивления при изгибе вычисляется по формуле

W. = 21. /h ,                  (3)

где I X - момент инерции сечения относительно оси Х-Х.

Для швеллера на рис. 3

th^{3 1} х ~

Выразив ширину полок швеллера через ширину

+ 2 ^bt (h)²                   (4)

исходной полосы S , после

подстановки b в формулу (4) и преобразований получим b = ^

После подстановки b в формулу (4) получим

1. = v^+s-*)4 (s -^

Тогда момент сопротивления швеллера будет равен th²         2h 2     th

^W > =-^{(s -} 4-)» = т V

Продифференцируем W X по h

2Ж , = я -2^₌t(£-S.

dh       2       3        \2     3 .

-

23h)

Приравняв производную нулю, получим

\ 2

t (2 - 3 h ) = 0 ,

Откуда               h = -3-S                (7)

Вторая производная меньше нуля

Cледовательно, выражение (7) определяет высоту гнутого швеллера, соответствующую максимальному моменту сопротивления W max (рис. 4).

Ширина полки швеллера b=(s-ℎ)=i(5- 4^)= I =       (8)

Максимальный момент W max по формуле (5) с учётом установленного оптимального значения высоты швеллера h= 3/4 S

W_{max =}  ^(s- 3 4^)=<        0)

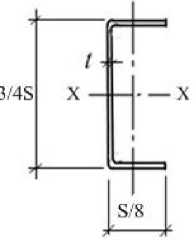
Рисунок 4 – Оптимизированное сечение швеллера

Установим, как соотносятся между собой моменты сопротивления стенки и полок швеллера.

Момент сопротивления стенки швеллера wст=^ =(-s)2=              (10)

ст 6     6 \4 /      32                  X '

Вычтя из W max по формуле (9) момент сопротивления стенки W СТ по формуле

(10), определим момент сопротивления двух полок швеллера

...    3tS2 3tS2 3tS2

W = ^п 16

-

32     32

Следовательно, в оптимальном сечении гнутого швеллера момент сопротивления стенки равен сумме моментов сопротивления двух полок.

Выводы. 1. В оптимально запроектированном сечении гнутого швеллера высота стенки равна 3/4 ширины исходной заготовки (полосы), ширина полки – 1/8 ширины исходной полосы. При этом момент сопротивления стенки швеллера равен сумме моментов сопротивления двух его полок.

• 2.    Установленные оптимальные соотношения размеров элементов гнутого швеллера целесообразно использовать при проектировании и изготовлении прогонов покрытия.