Оптимизация размещения на акватории сил и средств поисково-спасательной службы: модель зимнего периода

Вопросы обеспечения безопасности людей на водных объектах находились и находятся в зоне пристального внимания Правительства Российской Федерации. Так, в соответствии с Федеральным законом от 27.01.2023 № 4-ФЗ «О внесении изменений в отдельные законодательные акты Российской Федерации»1 были внесены дополнения по обеспечению безопасности людей на водных объектах.

Президент Российской Федерации в своем Указе от 16.10.2019 № 501 «О Стратегии в области развития гражданской обороны, защиты населения и территорий от чрезвычайных ситуаций, обеспечения пожарной безопасности и безопасности людей на водных объектах на период до 2030 года»2 поставил конкретные задачи перед руководителями субъектов РФ по обеспечению безопасности людей на водных объектах, снижению количества происшествий и числа погибших на воде.

Приказом от 15 февраля 2021 года № 71 Министерство экономического развития Российской Федерации утвердило Методические рекомендации для субъектов Российской Федерации по подготовке нормативов градостроительного проектирования3. В рекомендациях, в частности, установлено, что минимальная обеспеченность спасательными станциями (далее – СПС) и спасательными постами (далее – СП) на акваториях должна составлять не менее двух СПС или СП на каждые 1000 человек отдыхающих при условии, что расстояние до любой точки обслуживаемой территории водного объекта в зоне спасания не должен быть более 200 м.

На основании методических рекомендаций для субъектов РФ в Санкт-Петербурге в 2023 году правительством Санкт-Петербурга разработана новая редакция по подготовке и утверждению нормативов градостроительного проектирования, где определен показатель обеспеченности спасательными станциями не менее 1 единицы на каждые 15 км береговой линии водных объектов.

Обзор литературы

Анализ научных трудов и литературы по заявленной теме показывает, что научные исследования по указанной теме в прямой постановке вопроса практически не проводились, не говоря уже о создании математических моделей, позволяющих решить вопросы оптимального размещения на акватории спасательных подразделений.

Вопросы размещения спасательных сил и средств, точнее, взаимного их расположения в существующих международных и отечественных научных работах, международных конвенциях и литературе рассматриваются только применительно к процессу поиска, то есть

Вестник Российского нового университета

Серия «Сложные системы: модели, анализ и управление», выпуск 2 за 2025 год в ходе проведения поисковых и спасательных операций на акваториях. При этом очень подробно описаны маршруты движения поисковых средств, необходимых для обнаружения объекта поиска, наряд сил для увеличения вероятности успешного проведения поисковых и спасательных действий и др.

Особенно подробно разработаны вопросы взаимодействия различных поисково-спасательных сил и средств при проведении совместных действий на акватории. В первую очередь это бассейновые планы поиска и спасания людей на акватории, требования международных конвенций и национальных нормативных правовых актов, при этом вопросы размещения спасательных сил и средств на акватории практически не рассматриваются. Не рассматриваются вопросы о моделях и методах построения и размещения на акватории сил и средств поисково-спасательной службы ни в научной, ни в учебной литературе МЧС России [1–5].

В учебной литературе МЧС России главное место отведено вопросам подготовки спасателей при проведении поисково-спасательных мероприятий на акватории.

Не нашли должного отражения вопросы моделирования размещения на акватории сил и средств поисково-спасательной службы в научных трудах и публикациях ВНИИ ГОЧС (НИИ ГПС МЧС России). В них, как и в целом в учебной и научной литературе, главное внимание уделено вопросам пожарной безопасности, а вопросы обеспечения безопасности людей на акваториях не рассматриваются. В то же время вопросы моделирования и методы построения и размещения сил и средств противопожарной службы достаточно подробно представлены в научных работах и публикациях, в том числе при защите диссертаций [6–9]. Все они изначально базируются на действующих нормативных актах, принятых в МЧС России.

При изучении степени научной разработанности проблемы были проанализированы некоторые научные работы Санкт-Петербургского университета Государственной противопожарной службы Министерства Российской Федерации по делам гражданской обороны, чрезвычайным ситуациям и ликвидации последствий стихийных бедствий имени Героя Российской Федерации генерала армии Е.Н. Зиничева, в частности [8; 9]. Цель анализа – выяснение возможности применения математического аппарата моделирования, разработанного в диссертациях, к решению задачи по созданию модели и разработки метода построения и размещения на акватории сил и средств поисково-спасательной службы.

В изученных работах при разработке темы в качестве исходных точек расчета были взяты узаконенные требования МЧС России к пожарным частям4. Подробно расписаны типы пожарных депо, их количество, количество в них пожарных автомобилей и техники, а также зависимость между ними и числом жителей в населенном пункте. Установлены и нормативы расстояний (радиусы реагирования) пожарных депо, которые не должны превышать 3 км.

Всего этого (населенные пункты, дороги) нет на акваториях, не утверждены нормативы размещения на акватории сил и средств поисково-спасательной службы ни в документах МЧС России, ни в документах субъектов Российской Федерации, регламентирующих

Оптимизация размещения на акватории сил и средств поисково-спасательной службы: модель зимнего периода вопросы обеспечения безопасности людей на водных объектах (акваториях). Поэтому методики, разработанные для пожарных частей, применить к моделированию построения и размещения на акватории сил и средств поисково-спасательной службы не представляется возможным.

В то же время в широком смысле вопросы моделирования и решения различных задач оптимального размещения объектов различного типа (мобильных, стационарных) рассматривались в достаточном количестве работ как отечественных, так и зарубежных ученых [10–13].

Анализ этих работ показывает большое разнообразие используемых моделей, применимых для решения однотипных задач, разные методы решения задач оптимального размещения с учетом случайных факторов (статистические данные о событиях и др.) и при наличии ограничений [6; 7]. Например, в [9] один из разделов научной работы озаглавлен как «Математические модели размещения поисково-спасательных подразделений на внутренних водоемах». Но так как тема научной работы – математические модели управления, то в отдельном разделе о размещении поисково-спасательных подразделений главное внимание уделено определению их минимального количества с точки зрения экономической целесообразности в рамках выделяемых средств.

При разработке темы настоящей статьи упомянутая выше модель размещения поисково-спасательных подразделений на внутренних водоемах может быть частично применена к расчету количества спасательных постов на пляжах, но только в летнее время и с большой натяжкой, так как жестко привязана к количеству людей, находящихся в данной области водоема.

Таким образом, актуальной является задача выработки общего (универсального) подхода к решению задачи оптимального построения модели размещения на акватории сил и средств поисково-спасательной службы.

Статистические данные для моделирования

Для построения модели был проведен анализ несчастных случаев, происшествий и чрезвычайных ситуаций (далее – ЧС) за последние 10 лет на акватории, пляжах и объектах морской и речной инфраструктуры Санкт-Петербурга. Кроме того, проведен анализ использования на акватории сил и средств территориального пожарно-спасательного гарнизона Санкт-Петербурга.

Одной из основных задач Санкт-Петербургского государственного казенного учреждения «Поисково-спасательная служба Санкт-Петербурга» (далее – ПСС Санкт-Петербурга или Служба) является проведение аварийно-спасательных работ, в том числе работ по поиску и спасению терпящих бедствие людей на водных объектах. В соответствии с методическими рекомендациями Комитета по вопросам законности, правопорядка и безопасности Санкт-Петербурга в ПСС Санкт-Петербурга организована работа по сбору статистических данных о происшествиях на водных объектах города, мерах, принятых для ликвидации ЧС и их последствий, о случаях гибели людей, об авариях маломерных судов. Такие данные ежедневно заносятся оперативным дежурным ПСС в специально разработанную форму программы Miсrosoft Excel.

Таким образом, в ПСС Санкт-Петербурга накапливаются статистические данные по обстановке на водных объектах города, которые затем анализируются для принятия управленческих решений и подготовки докладов в Комитет о результатах деятельности Службы.

Вестник Российского нового университета

Серия «Сложные системы: модели, анализ и управление», выпуск 2 за 2025 год

Данные собираются и анализируются с 2014 года. Статистические данные о происшествиях на водных объектах представлены на Рисунке 1.

Происшествия с людьми           Происшествия с МС                  Погибло

■ 2014    ■ 2015    «2016    «2017    «2018    «2019 В2О2О 12021    >2022    «2023

Рисунок 1. Статистические данные о происшествиях на водных объектах в Санкт-Петербурге Источник: здесь и далее схемы рисунки предоставлены СПБ ГКУ «Поисково-спасательная служба Санкт-Петербурга».

Одним из главных вопросов, который необходимо решить для улучшения безопасности людей на водных объектах города, – уменьшение времени прибытия спасательных сил и средств к месту возникновения ЧС, что напрямую связано с оптимальным размещением спасательных станций.

Сложностей в этом вопросе много: постоянное увеличение числа граждан, отдыхающих на водных объектах города летом и рыбаков в зимний период. Частая ненастная и переменчивая погода создает сильное волнение на акватории, уменьшает видимость, а зимой способствует изменению характера ледяного покрова и возникновению торосов.

На акватории Невской губы и Финского залива в административных границах города размещены оставшиеся еще с советских времен 10 спасательных станций. Их размещение на побережье не совпадает с размещением официальных городских пляжей, соответственно, не способствует в должной мере уменьшению времени прибытия спасательных судов в любую возможную точку бедствия на акватории.

Это еще раз подчеркивает необходимость разработки модели оптимального размещения на акватории сил и средств поисково-спасательной службы для уменьшения времени прибытия спасателей к месту бедствия на водном объекте и увеличения вероятности спасания людей.

Математическое моделирование

Для достижения поставленной цели моделирования были решены следующие вопросы:

• •    сбор статистических данных о гибели людей на водных объектах Санкт-Петербурга;

• •    анализ статистических показателей гибели людей на водных объектах и возникновения происшествий с людьми и маломерными судами;

• •    выбор и сопоставление различных методов решения вопроса по оптимизации размещения на акватории сил и средств поисково-спасательной службы;

Оптимизация размещения на акватории сил и средств поисково-спасательной службы: модель зимнего периода

• •    разработка математической модели оптимального размещения на акватории сил и средств поисково-спасательной службы;

• •    создание компьютерной программы для решения задачи в соответствии с математической моделью.

Обоснование необходимости поставленных целей было выведено из «аксиомы успеха»: «чем быстрее к месту бедствия на воде или месту возникновения чрезвычайной ситуации прибудут спасательные силы и средства, тем выше вероятность спасения людей, терпящих бедствие, и меньше ущерб от ЧС».

Настоящая работа посвящена построению имитационных моделей и применению методов оптимизации размещения спасательных станций с учетом различных факторов: плотность водного движения; данные о предыдущих происшествиях; географические особенности района и др.

Основная цель исследования – разработка математической модели, которая позволит определить места размещения спасательных станций, обеспечивающих высокую эффективность их деятельности, под которой подразумевается степень соответствия результатов деятельности поставленным задачам.

В настоящий момент вся акватория в границах Санкт-Петербурга вплоть до Ленинградской области поделена между десятью станциями (см. Рисунок 2).

Рисунок 2. Карта зон ответственности спасательных станций

За основу моделирования принято следующее:

1) определение оптимальной позиции для установки одной или нескольких дополнительных спасательных станций;

2) оценка эффективности актуального разделения зон ответственности между станциями: насколько, исходя из анализа построенной имитационной модели, разбиение ак-

Вестник Российского нового университета

Серия «Сложные системы: модели, анализ и управление», выпуск 2 за 2025 год ватории в настоящий момент времени близко к оптимальному, что можно изменить для уменьшения ключевых параметров работы СПС – среднее/максимальное время реагирования станций на очередное происшествие и увеличение вероятности спасания.

Здравый смысл подсказывает, что для таких случаев требуется рациональное распределение ресурсов СПС, что, в свою очередь, требует введения классификации типичных происшествий и чрезвычайных ситуаций, требующих ответных действий. Выделяя наиболее часто возникающие случаи, можно заметить следующее.

Характерные случаи летом:

• •    человек в воде;

• •    маломерное судно, которое терпит бедствие;

• •    поиск и подъем утонувшего.

Характерные случаи зимой:

• •    рыбаки (люди) на льду;

• •    человек провалился под лед;

• •    дети на льду;

• •    отрыв льдины с людьми.

Исследование проводилось на основе статистических данных о действиях ПСС Санкт-Петербурга, относящихся к ЧС на акватории Финского залива в зимний период. Необходимо отметить, что безопасное время пребывания человека в условиях низких температур воздуха и воды на льду при сильном ветре и высокой влажности воздуха минимально и значительно меньше, чем в летний период.

Модель длительности выживания человека в воде

Существует литература, посвященная данной проблеме, с учетом различных факторов, таких как температура воды, параметры человека, терпящего бедствие, и др. Хорошим примером является статья [14].

Для наших целей, однако, вполне приемлема грубая модель, отражающая качественную картину с резко возрастающей интенсивностью смертности (соответствующий актуарный термин – «сила смертности»). Предлагаем простую двухпараметрическую модель, один из параметров которой 0 - предельное время пребывания в холодной воде, другой - параметр масштаба у .

Выберем параметризацию интенсивности смертности в виде

r (t ) =

Y (0-t )2

,0 <  t < 0.

Вероятность того, что (случайное) время жизни в холодной воде будет не менее t ми- нут при данной параметризации

exp

4 0 r ⁽ s ) ds

= Y

0 — 0—7

,0< t < 0.

В качестве оценки для параметра 0 можно выбрать 0 - максимальную за время наблюдений продолжительность жизни в холодной воде.

Для параметра масштаба Y можно использовать оценку максимального правдоподобия, взяв наблюдаемую статистическую медиану m продолжительности жизни в холодной воде:

Оптимизация размещения на акватории сил и средств поисково-спасательной службы: модель зимнего периода

0 ( 0 - m )

Y= In 2—-----’-

.

m

На основании открытых данных о температуре воды в Финском заливе в интересующий нас период и с учетом статистических данных о средней продолжительности жизни людей в холодной воде при подобных температурных условиях были выбраны значения параметров, отражающие реалистичные сценарии выживания. Эти параметры также согласуются с характерными данными, представленными в литературе, и позволяют адекватно моделировать интенсивность смертности в рамках предложенной модели (см. Рисунок 3):

0 = 25 мин , m = 10 мин ,

Y® 25,96

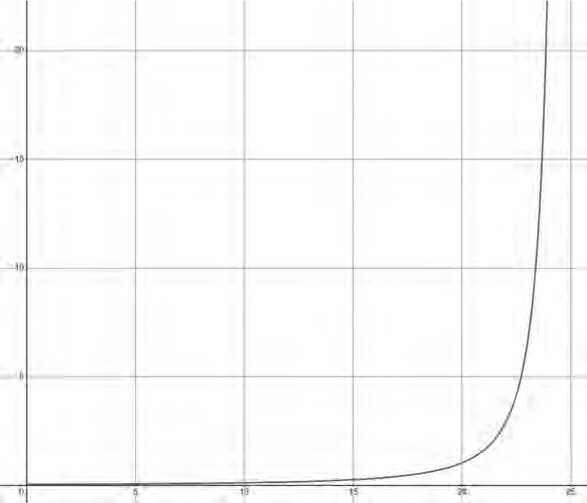
Рисунок 3. График интенсивности смертности с параметрами 0 = 25 мин , m = 10 мин Пространственная модель возникновения происшествий

В качестве основы для имитационной модели возникновения происшествий выбрано пуассоновское случайное поле (также называемое пуассоновским точечным процессом). Пуассоновское поле является специальной моделью случайного множества, которое более чем счетно и задается при помощи моментной меры Л ( A ) - среднего числа точек в множестве A . Обычно предполагается, что эта мера является неатомической, то есть одноточечные множества имеют нулевую меру.

Суть модели состоит в том, что количество точек v ( A i ) в попарно не пересекающихся множествах A i , является взаимно независимой величиной, и случайная величина v ( A ) имеет пуассоновское распределение с параметром Л ( A ) .

Вестник Российского нового университета

Серия «Сложные системы: модели, анализ и управление», выпуск 2 за 2025 год

В частном случае для пуассоновского поля в конечномерном евклидовом пространстве часто выбирается моментная мера, представляемая в виде

Л( A) = jx( x) dx,

A где X(x) - интенсивность поля в точке x . Такое представление будет использоваться для двумерного случая.

Способ моделирования пуассоновского поля (методом Монте-Карло) описан, например, в статье Ю.К. Беляева «Пуассоновский точечный процесс» [10].

Статистическая оценка интенсивности поля возможна различными способами, например, при помощи имеющейся статистической информации в журнале оперативного дежурного Службы.

В ПСС Санкт-Петербурга на основе наблюдений была составлена карта мест повышенной опасности (см. Рисунок 4). Это позволило построить грубую модель, корректно описывающую реальность с удовлетворительной для практики точностью.

Рисунок 4. Зоны повышенной опасности в зимний период

Когда имеется статистика в виде выборки местоположения чрезвычайных происшествий, то есть ряд точек z _i = ( x _i , y _i ), где x _i и y _i – координаты каждого происшествия; эту вы-

Оптимизация размещения на акватории сил и средств поисково-спасательной службы: модель зимнего периода борку можно использовать для оценки интенсивности пуассоновского случайного поля. Одним из методов оценки интенсивности является ядерное сглаживание. Для каждой точки z можно оценить интенсивность Х(z) как сумму «сглаженных» вкладов всех происшествий вокруг нее, взвешенных в соответствии с расстоянием от точки z в виде

% ( z ) = ¹ П К\ — ^У ’ n t l I h

,

где K – ядерная функция; h – ширина окна сглаживания; n – количество происшествий;

II z — Z i II — расстояние между точками z и z i .

Одной из наиболее часто используемых ядерных функций является гауссово ядро:

K ( u )

1     -

2 u

e

V 2 n

Если выборка местоположений отсутствует или является неполной, что соответствует ситуации в нашем случае, полезна информация в виде карт, на которых выделены области с повышенной плотностью происшествий. Так, на Рисунке 4 представлена карта, на которой отмечены зоны повышенной опасности на льду Финского залива в зимний период.

Сложные области в двумерном пространстве логично аппроксимировать смесью из нескольких гауссовых распределений. В нашем случае область представляет собой кластеризацию данных, где каждый кластер (стоянка рыбаков) имеет свою собственную форму и интенсивность (среднее количество людей).

Модель смеси гауссовых распределений представляет собой смесь нескольких гауссовых компонент, каждая из которых описывает свой собственный кластер данных. Пусть у нас есть область данных X = {x1, x2, . . ., xN} в двумерном пространстве, состоящая из N точек, где каждый элемент xi е R2. Плотность аппроксимирующего распределения может быть определена следующим образом:

K

Р (x ) = tni ^ (хЦi, 2 i), i=1

где K - количество компонент в смеси; ni - весовой коэффициент i-й компоненты, определяющий ее вклад в общую смесь (и обеспечивающий нормировку суммы до единицы); N (x | цi, Si) - многомерное гауссово распределение с математическим ожиданием цi и ковариационной матрицей Σi:

exp

,

^ (x Ц, 2) = 2п |2

где x , ц е R², S е R^2x2, |S| - определитель ковариационной матрицы.

Функция p(x) представляет собой сумму плотностей всех компонент метода для за- данного значения x, то есть вероятность наблюдать x в данных, учитывая все компоненты.

Для аппроксимации сложной области смесью из трех гауссовых распределений необходимо оценить параметры каждой компоненты. Параметры, которые нужно оценить для каждой компоненты, включают в себя среднее значение ц и ковариационную матрицу Σi. Это может быть сделано с помощью алгоритма оценки параметров, такого как метод максимального правдоподобия.

Значения n i , которые определяют вклад каждой компоненты в общее распределение, в данной модели уже найдены. Их можно вычислить по формуле

Вестник Российского нового университета

Серия «Сложные системы: модели, анализ и управление», выпуск 2 за 2025 год

1 ^N i,max + ^N i,_mn

П =               , i N 2

где N _i,max и N _i,min – верхняя и нижняя границы количества рыбаков, указанных на i -й стоянке

„  ^Ni,max + Ni,mn на карте; N = £ i,max   „„n – нормирующий коэффициент, несущий смысл среднего общего количества рыбаков на льду.

Оптимизация размещения станций

Задача оптимизации на плоскости принимает следующий вид: нужно найти множество M точек (станций) M = { v 1 , V₂,-, V _M } на плоскости, минимизирующее среднее максимальное расстояние от возникающего вызова до ближайшей станции, то есть минимизирующую функцию

Ф ( ^ 1 , V 2 ,-, V м W^inР ( x , V i ) Q ( dx ) .

Такая постановка предлагалась в [11], однако там не было ограничений на положение станций в пространстве, что приводит к M -ранговой задаче оптимизации. Будем далее считать, что носитель Q ограничен, а распределение Q имеет плотность q , интегрируемую по Риману.

В приближенных к реальности условиях надо учесть, что уже установленные станции вряд ли получится переместить, и по факту для M станций, k из которых фиксированы, мы имеем дело с задачей меньшей размерности ( M – k ):

^ф ( V 1^, V 2 ,^, V k | V k + 1 ,^, V M M minp ( x , V i ) Q ( ^dx ) = ^ф * ( v k + 1 ,^, V M ) .

Кроме того, следует учитывать, что станции располагаются на побережье материка или островов, так что они могут менять своё положение лишь в рамках данного одномерного пространства.

С учетом размерности задачи (10–12 станций) в качестве метода оптимизации разумно взять одну из модификаций градиентного спуска, например, Adam (Adaptive Moment Estimation), потому что он эффективно адаптирует скорость обучения для каждого параметра на основе первых и вторых моментов градиента и может справляться с наличием локальных минимумов благодаря стохастической природе обновлений. Adam также подходит для задач, где целевая функция имеет сложный ландшафт, включая плоские участки, седловые точки и шум [13].

Рассмотрим задачу оптимизации размещения спасательных станций в фиксированном районе акватории. Пусть M – количество спасательных станций, которое необходимо разместить, и N – количество случайных происшествий, которые могут происходить в акватории. Каждое происшествие характеризуется координатами ( x i , y i ) , а каждая станция -координатами ( X j , Y j ) . Цель - минимизировать среднее время достижения до каждого происшествия от ближайшей станции.

Рассмотрим вариант с береговыми спасательными станциями, для этого перепишем задачу. Параметризуем координаты береговой линии. Пусть функция J ( ■ ) однозначно задает береговую линию:

J ^: u j ^ ( X j , Y ) = v ₇ , u XM.

Функция стоимости (целевая функция) – это максимальная из длин пути от всех сгенерированных происшествий до ближайших им станций:

Оптимизация размещения на акватории сил и средств поисково-спасательной службы: модель зимнего периода

f (J (и )) = f * (и) = max min р (xi, у j) = max min p (xi, J (Uj))

Иными словами, f ( и ) - это функция стоимости, где и = ( и 1 ,...,и_м ) - вектор параметризованных координат всех M станций.

В действительности задача оптимизации принимает упрощенный вид: если в настоящий момент расставлено уже 10 станций, дальнейшая оптимизация представляет собой расстановку одной (максимум двух) станций. То есть задача представляет собой минимизацию функционала

Ф* (у*) = Ф1 (Vi,У2,., Vie|У*) = !minр(x, V,)Q(dx)

по параметру u :

Ф ( J ( u ))^ min, u e D где D может представлять собой D = [0,1](M k) в зависимости от размерности задачи. В данном случае (M - к) < 2, поэтому можно не сомневаться: оптимизатор Adam справится с задачей.

Результаты экспериментов

В первую очередь проведем анализ сложившейся на настоящий момент инфраструктуры, расположения действующих спасательных станций.

Применяя алгоритм нахождения кратчайшего маршрута до N = 15000 сгенерированных происшествий на изначальной расстановке, получим следующую картину (для большей читаемости на графике обозначена каждая 10-я точка) (см. Рисунок 5).

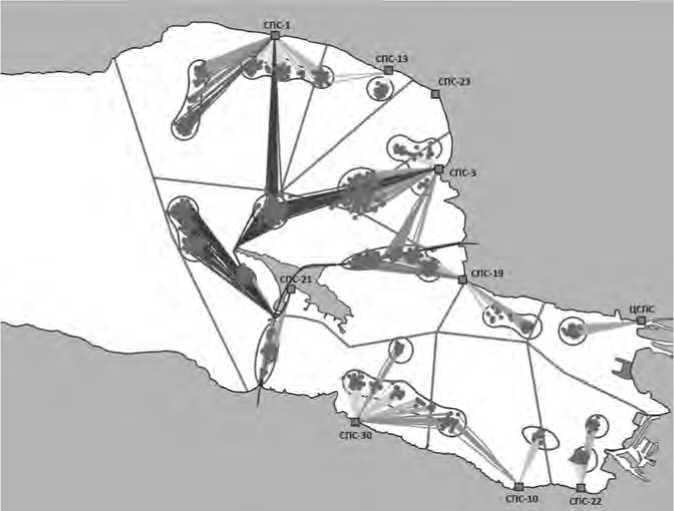
Рисунок 5. Кратчайшие пути при нынешней конфигурации станций

Вестник Российского нового университета

Серия «Сложные системы: модели, анализ и управление», выпуск 2 за 2025 год

Чем темнее фиолетовый оттенок, тем больше времени понадобилось для реагирования на ЧС. Как видим, при нынешней расстановке самые труднодоступные точки расположены за островом Котлин, так как на северной стороне спасательные станции расположены только на материке и спасательным расчетам СПС № 21 (единственной станции, расположенной на территории острова Котлин) приходится полностью огибать остров. При одномерной оптимизации оптимальная точка размещения СПС будет находиться на северной стороне острова, ближе к его пику. Результаты дальнейших экспериментов представлены в Таблице 1.

Таблица 1

Значения ключевых параметров при разных конфигурациях размещения станций

Значения	noOpt	Одномерный случай		Двумерный случай
		maxTimeOpt	meanTimeOpt	maxTimeOpt	meanTimeOpt
t пер,ср (мин)	10,45	7,39	7,37	7,93	6,78
t пер,макс (мин)	22,04	15,79	15,83	13,43	16,22
р выж,ср	0,474	0,646	0,649	0,616	0,679
р выж,мин	0,0004	0,168	0,166	0,301	0,146

Обозначения:

tпер (мин) - время прибытия к тонущему tпер>ср (мин) — среднее время прибытия tпер,макс (мин) — максимальное время прибытия

Р ^ыж,_ср — средняя выживаемость

Р _Выж,мин - наихудшая выживаемость

В случае с одномерной оптимизацией результат вполне совпал с нашими предположениями: точка, в которую нужно поставить станцию при минимизации как среднего, так и максимального времени реагирования, располагается на серверном мысу острова Котлин (см. Рисунок 6).

При этом наблюдается снижение обоих ключевых параметров – среднего и максимального времени реагирования – примерно на 30 %, что является значительным улучшением, учитывая, что добавили всего одну станцию к десяти существующим.

Напротив, при двумерной оптимизации можно наблюдать неоднозначность выбора. Если в качестве ключевого параметра выступает среднее время реагирования, то получим расстановку, где обе новые станции располагаются на северной части острова Котлин (см. Рисунок 7).

Если отдать приоритет наименьшему времени реагирования, то расстановка принимает вид, как на Рисунке 8.

Оптимизация размещения на акватории сил и средств поисково-спасательной службы: модель зимнего периода

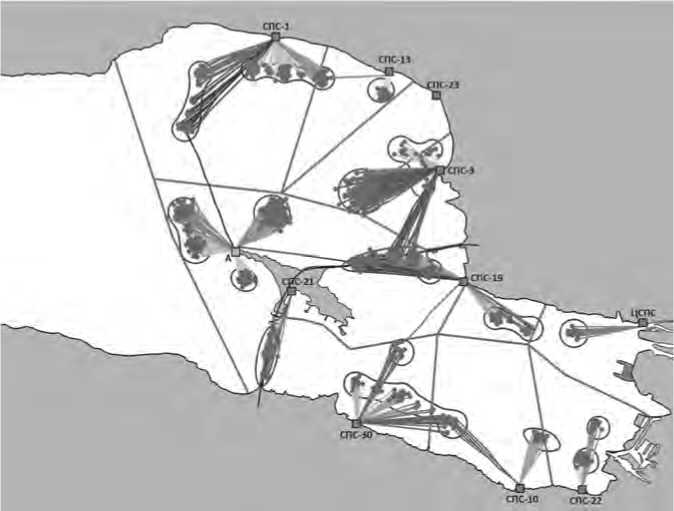
Рисунок 6. Оптимальное размещение первой добавленной станции

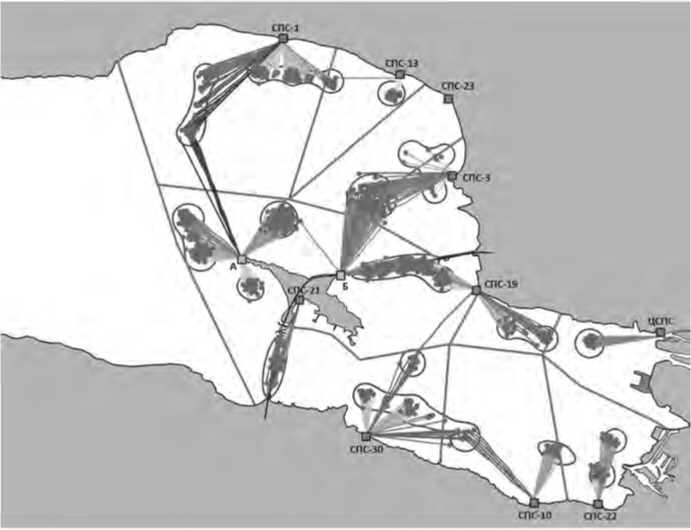
Рисунок 7. Оптимальное размещение двух добавленных станций (по среднему времени)

Вестник Российского нового университета

Серия «Сложные системы: модели, анализ и управление», выпуск 2 за 2025 год

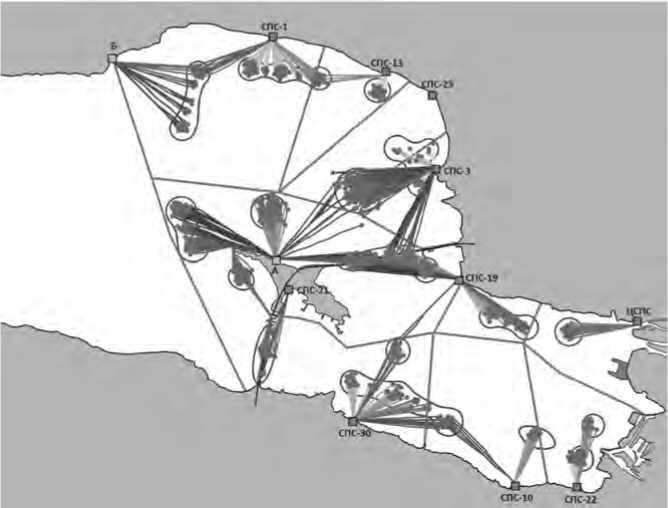
Рисунок 8. Оптимальное размещение двух добавленных станций (по максимальному времени)

Для наглядности вынесем относительные приросты в Таблицу 2.

Таблица 2

Значения ключевых параметров

Значения	noOpt, %	Одномерный случай		Двумерный случай
		maxTimeOpt, %	meanTimeOpt, %	maxTimeOpt, %	meanTimeOpt, %
A t nep.cp	0	29	29	24	35
△ t пер,макс	0	28	28	39	27
Д P выж,ср	0	36	36	30	43

Итого, можно получить три разные расстановки станций, каждая из которых в некотором плане оптимальна в зависимости от возможностей инфраструктуры и приоритетов.

Оценка эффективности размещения

Под эффективностью спасательной станции подразумевается то, насколько велик вклад данной станции в общую картину. Рассмотрим следующую карту (см. Рисунок 9).

На данном изображении, полученном по результатам работы программы, СПС № 23 (оранжевая, сверху справа) прикрывает район меньший по площади, чем соседние № 3 и № 13. Это значит, что почти в каждую точку выделенной СПС № 23 зоны ответственности спасатели из СПС № 23 доберутся медленнее, чем спасатели из соседних № 13 и № 3. Вывод – в зимнее время СПС № 23 неэффективна.

Оптимизация размещения на акватории сил и средств поисково-спасательной службы: модель зимнего периода

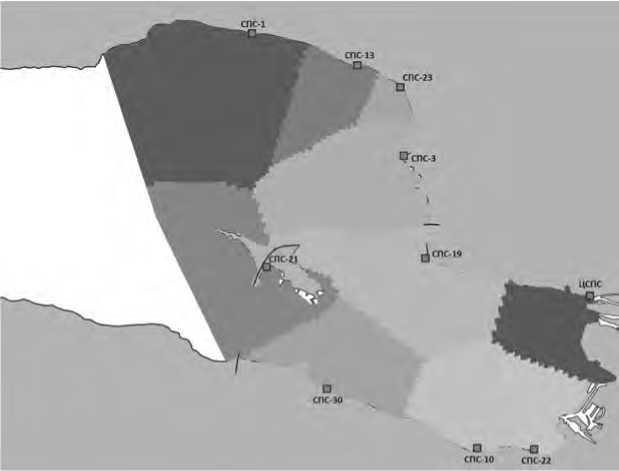
Рисунок 9. Разделение зон ответственности, актуальная конфигурация станций

В частности, ни в одном из проведенных выше экспериментов (см. Рисунки 5–8) оптимальные траектории не выходили из этой станции.

Надо отметить, что летом ситуация может измениться, так как северное побережье Финского залива покрыто пляжами, и в таких условиях станция СПС № 23 будет более востребована.

Еще несколько примеров карт, наглядно отражающих полученную картину неэффективности СПС № 23 в зимнее время (см. Рисунки 10–12).

Вестник Российского нового университета

Серия «Сложные системы: модели, анализ и управление», выпуск 2 за 2025 год

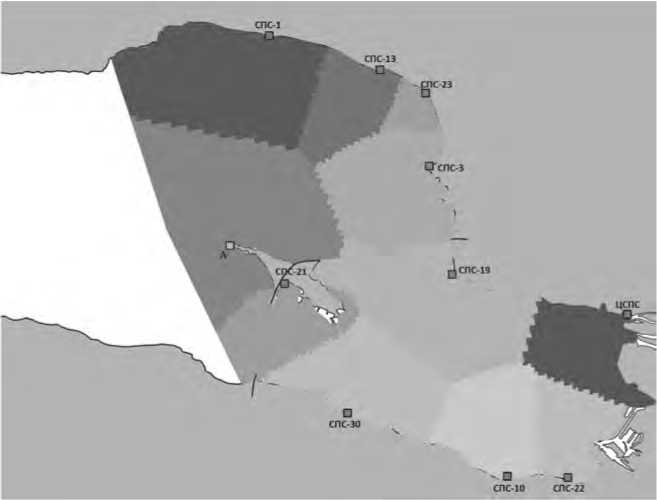
Рисунок 10. Разделение зон ответственности, одна добавленная станция

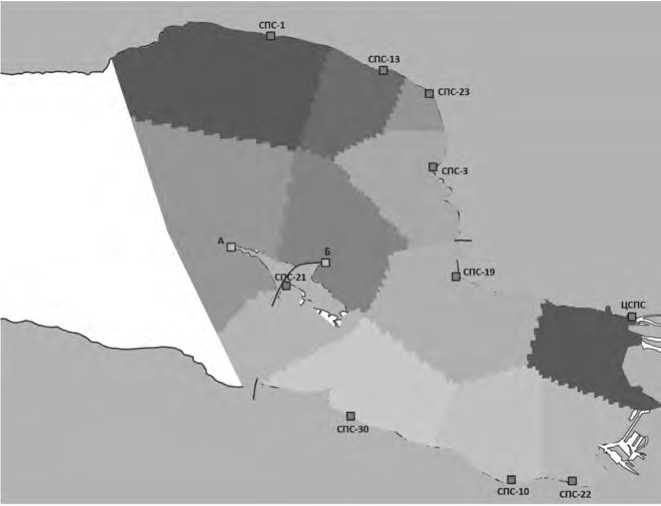
Рисунок 11. Разделение зон ответственности, две добавленные станции (оптимальное среднее время)

Оптимизация размещения на акватории сил и средств поисково-спасательной службы: модель зимнего периода

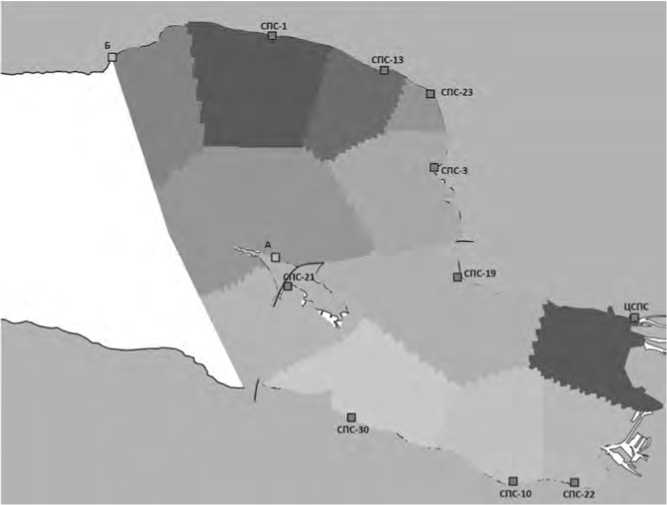
Рисунок 12. Разделение зон ответственности, две добавленные станции (оптимальное максимальное время)

Выводы

В ходе данного исследования была проведена работа по оптимизации размещения спасательных станций в заданной акватории, по результатам которой сделаны следующие выводы.

• 1.    На основе методов теории вероятностей, алгоритмов нахождения кратчайших путей и методов глобальной оптимизации удалось разработать эффективную модель оптимального размещения на акватории сил и средств поисково-спасательной службы для минимизации времени реагирования на чрезвычайные происшествия.

• 2.    Результаты исследования показали, что предложенная модель позволяет значительно сократить время реагирования спасательной службы на ЧС, что непосредственно влияет на вероятность успешного спасания пострадавших.

• 3.    Данный подход может быть применен в различных контекстах, связанных с оптимизацией расположения аварийно-спасательных служб и ресурсов:

• а) разместить новую спасательную станцию в форте «РИФ» острова Котлин, так как СПС № 23 в зимний период использовать неэффективно;

• в) в целях рационального использования спасательных сил и средств, расположенных на СПС № 23 в зимний период, перебазировать их в 1-й Северный форт.

• 4. Таким образом, проведенное исследование не только подтвердило эффективность предложенных методов, но и доказало их практическую применимость. Полученные результаты могут служить основой для дальнейших исследований и разработок в области оптимизации размещения спасательных сил и средств поисково-спасательной службы.

Вестник Российского нового университета

Серия «Сложные системы: модели, анализ и управление», выпуск 2 за 2025 год