Оптимизация рецептуры кормов непродуктивных животных с помощью математического моделирования

Одной из фундаментальных проблем пищевых производств является производство высококачественных продуктов питания при максимально полезном использовании пищевого сырья. При этом полезным можно считать и использование вторичного пищевого сырья для разнообразных кормов для животных.

В настоящее время в российской пищевой промышленности идет активное развитие производств кормов для непродуктивных животных. Доля импорта на рынке кормов, например, для домашних животных составляет 76 % - сухих кормов, 85 % - консервированных.

В условиях усиливающейся конкурентной борьбы на рынке таких кормов и изменяющихся предпочтениях потребителей решение проблем снижения доли импорта возможно только на основе использования производственных инноваций.

Нестабильные качественные показатели сырья и взаимодействие компонентов смеси между собой затрудняют построение полной математической модели. Поэтому моделирование рецептуры кормов для непродуктивных животных осуществляется с помощью аппарата нечеткой логики. Преимуществом данного метода является возможность проведения анализа в условиях субъективной оценки эмпирических данных и отсутствии явной числовой формы результата.

Особенно ярко преимущества этих систем проявляются при проектировании многокомпонентных пищевых продуктов, где велика неопределенность входных и выходных параметров, а качество оценивается по результатам сенсорного анализа. Сухой корм для непродуктивных животных относится к продуктам, обладающим данными характеристиками.

Так же достоинством модели является возможность ее получения при выборе минимального набора закономерностей. Вследствие отсутствия необходимости ввода точных данных, время, требуемое для моделирования, резко сокращается.

Аппарат нечеткой логики позволяет определить оптимальное соотношение рецептурных компонентов при проектировании новых многокомпонентных видов сухих кормов и сократить количество производственных опытов. Дополнительно он дает возможность повысить качество управления производством и контролем готового продукта в условиях информационной неопределенности, которая характерна для реального производства в отраслях пищевой промышленности.

Разработанная в настоящей работе математическая модель рецептуры многокомпонентных кормов для непродуктивных животных, подтверждена экспериментальными исследованиями.

Достоверность и обоснованность полученных результатов определяются корректным применением аппарата нечеткой логики, а выводы и предложения не противоречат известным практическим результатам, содержащимся в трудах специалистов по вопросам математического моделирования рецептур, в том числе моделирования рецептур кормов.

Для моделирования рецептуры сухого корма используется модуль Fuzzy Logic Toolbox, входящий в пакет MatLab [1]. Построение системы проводится на основе экспериментальных данных и сенсорного анализа.

Качество полученного продукта зависит от следующих показателей: значение рН среды (СанПиН 2.3.2.1078-01.), влажность (ГОСТ 50817-95), концентрация белкового компонента, размер частиц (ГОСТ Р 52427-2005), пищевая ценность, общая биологическая обсеме-ненность (ГОСТ Р 50454-92).

Желаемые диапазоны входных переменных:

• •    pH - 5 - 8;

• •    Влажность - vlajnost - 7 - 11%;

• •    Концентрация - concentration - 50 - 90%;

• •    Размер частиц - razmer_chastic - 0,3 - 0,8 мм;

• •    Пищевая ценность - pi_cennost - 100 -500 ккал/100 гр;

• •    Общая биологическая обсемененность -ob_bacteriol_obsemenennost - 0 - 1000 клеток в 1 г. корма.

Пример задания входных переменных отражен на рисунке 1. Редактирование выходной переменной производится аналогично редактированию входных переменных.

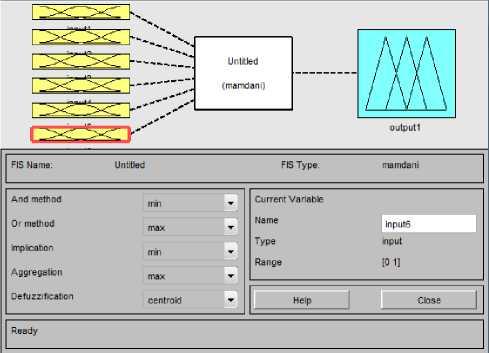
Рисунок 1. Задание входных переменных в систему

Тип функции принадлежности каждой переменной соответствует распределению по Гауссу (рисунок 2).

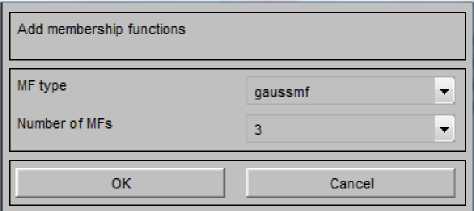
Рисунок 2. Выбор вида функции принадлежности и нечеткого вывода их количества

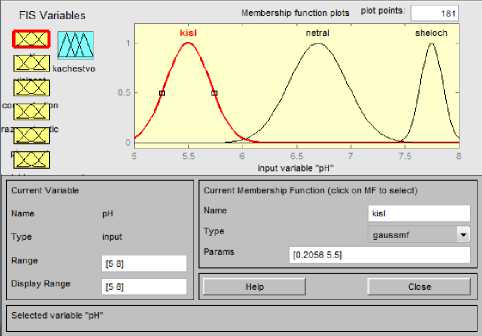
Рисунок 3. Задание характеристик входной переменной

Пример графика принадлежности функций после задания типа распределения отображен на рисунке 3.

Связь входных переменных с выходными задают правила ввода, которые должны быть включены в систему после построения функций принадлежности (рисунок 4). Для задания правил были установлены значения входных переменных, соответствующие наилучшим показателям качества:

• •    pH - 4-7,5, что соответствует «netral»;

• •    Влажность - vlajnost - 8 - 11%, что соответствует «sred» и «visokaya»;

• •    Концентрация - concentration – 60 - 90%, что соответствует « srednaya» и «visokaya»;

• •    Размер частиц - razmer_chastic - 0,5 - 0,6 мм, что соответствует «srednie»;

• •    Пищевая ценность - pi_cennost - 250 -300 ккал/100 г, что соответствует «horoshaya»;

• •    Общая биологическая обсемененность - ob_bacteriol_obsemenennost - 0 - 1000 клеток в 1 г. корма, что соответствует «dopustimaya».

  

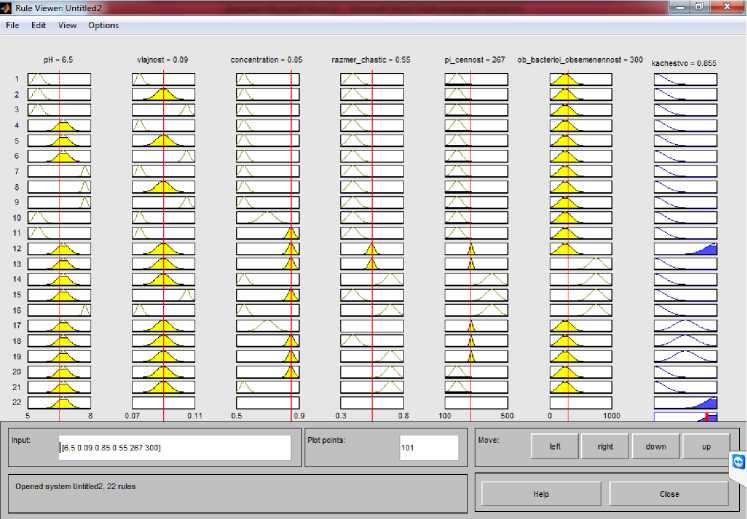
  Рисунок 4. Средства просмотра правил вывода переменной pH системы нечеткой логики

  
  

В окно задания базы знаний вводятся соответствующие правила, связывающие входные переменные с выходной.

Для визуализации нечеткого логического вывода используют команду View rules (рисунок 4). Данное средство просмотра правил позволяет отобразить процесс нечеткого логического вывода и получить результат.

Главное окно средства просмотра состоит из нескольких графических окон, располагаемых по строкам и столбцам. Количество строк соответствует числу правил нечеткого логического вывода, а количество столбцов – числу входных и выходных переменных, заданных в разрабатываемой системе. Дополнительное графическое окно служит для отображения результата нечеткого логического вывода и операции дефазификации.

В каждом окне отображается соответствующая функция принадлежности, уровень ее среза (для входных переменных) и вклад отдельной функции принадлежности в общий результат (для выходных переменных).

По результатам проведенного анализа были определены оптимальные значения параметров для достижения наилучших органолептических показателей, которые были оценены по поедаемости корма животными. Таким образом, было выявлено, что наилучшие органолептические характеристики достигаются при следующих значениях основных параметров: pH - 6,5; влажность - 9 %; концентрация белковой составляющей – 85 %; размер частиц -0,55 мм; пищевая ценность – 267 ккал/ 100 г.

Для представления результатов моделирования в графическом виде, используют модуль Surfase Viewer [2]. Средство просмотра поверхности вывода позволяет строить трехмерную поверхность как зависимость одной из выходных переменных от двух входных. Поверхность вывода, соответствующая благоприятному результату, окрашивается в желтый цвет, а не благоприятному результату окрашивается в синий цвет. Если результат соответствует некому среднему, промежуточному значению, то на графике эта область окрашивается в цвета градиентного перехода от желтого к синему (рисунки 5-9).

По результатам моделирования показателей качества кормов авторами были проведены практические исследования, подтвердившие эффективность использования данного метода при разработке новых продуктов с заданными качественными характеристиками.

Практические исследования проводились на животных различных пород, возрастных и гендерных категорий, не находящихся на естественном вскармвливании. В экспериментах приняли участие 74 животных.

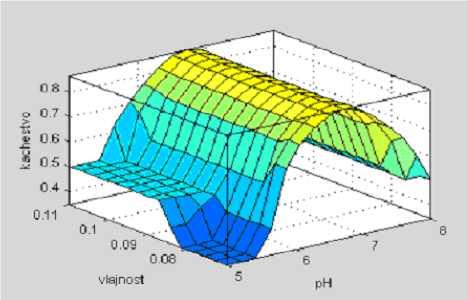
Рисунок 5. Зависимость качества от рН и влажности

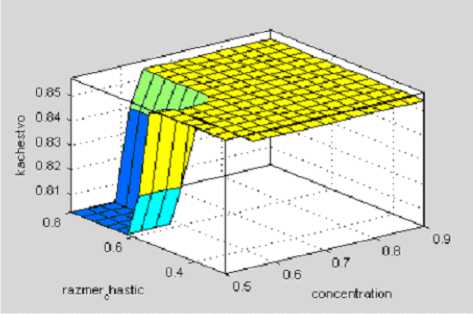
Рисунок 6. Зависимость качества от концентрации и размера частиц

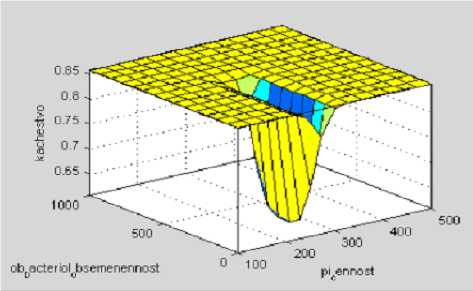
Рисунок 7. Зависимость качества от пищевой ценности

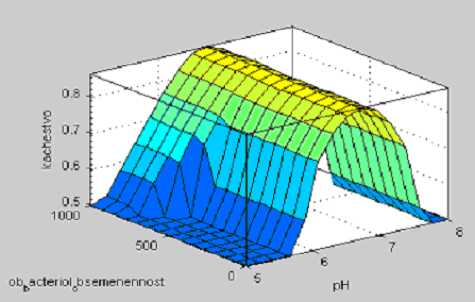
Рисунок 8. Зависимость качества от рН и ценности и биологической обсемененности

Была составлена рецептурная смесь для производства сухого кошачьего корма суперпремиум класса, в белковую составляющую которого входили мясо цыпленка, меланж сухой и молоко цельное сухое. Процентные соотношения ингредиентов рецептурной смеси и ее оптимальная влажность были определены экспериментальным путем.

В таблице 1 представлены рецептуры кормов, на диаграммах, изображенных на рисунках 9 и 10, отражены результаты эксперимента: зависимость поедаемости корма животным от рецептуры корма и зависимость поеда-емости корма от влажности.

Данный эксперимент подтвердил результаты математического моделирования методами нечеткой логики для входных характеристик концентрация белкового компонента и влажность рецептурной смеси [3].

Анализ показывал, что чрезмерное увеличение или наоборот - уменьшение влажности кормов ведет к ухудшению органолептических и микробиологических показателей качества кормов, а концентрация белкового компонента должна находиться на уровне 5070 %. Уменьшение доли белка ведет к снижению пищевой ценности кормов и привлекательности корма для животного, а увеличение доли белка ведет к излишним экономическим затратам и дисбалансу рациона питания.

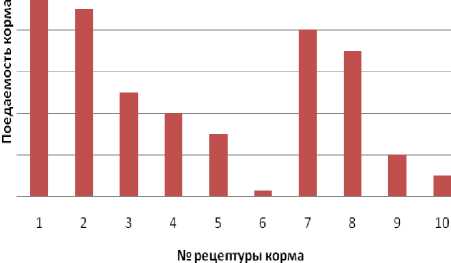
Рисунок 9. Поедаемость корма животным в зависимости от рецептуры кормов

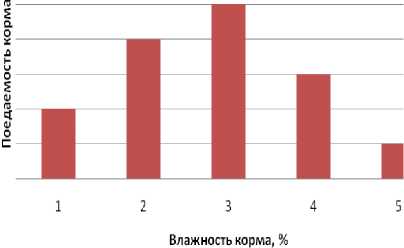
Рисунок 10. Поедаемость корма в зависимости от влажности

Т а б л и ц а 1

Рецептуры сухих кормов для непродуктивных животных

ИНГРЕДИЕНТЫ СМЕСИ	1	2	3	4	5	6	7	8	9	10
Мясо цыпленка, %	35	55	35	35	35	15	15	15	4	4
Рисовая мука, %	25	5	5	15	15	15	45	15	50	26
Меланж сухой, %	4	10	25	5	5	5	10	45	4	20
Молоко цельное сухое, %	12	10	15	25	5	45	10	5	4	20
Жир говяжий топленый, %	14	9	9	9	34	9	9	9	27	19
Вода, %	9	10	10	10	10	10	10	10	10	10
Дрожжи, %	1	1	1	1	1	1	1	1	1	1

Таким образом, можно сказать, что аппарат нечеткой логики может быть использован в производстве кормов для оптимизации количественных и качественных характеристик рецептурной смеси, усовершенствования управления процессами производства и контроля качества продукции, снижения затрат на внедрение нового вида сухого корма для домашних животных.

Проверка модели, разработанной в настоящей статье на основе нечеткой логики, строилась на классических методах математической статистики и базировалась на эмпирических данных [4].

Построенная математико-статистическая модель отражает зависимость потребления экструдированных пищевых продуктов (у) от рН среды (х 1 ), влажности готового продукта (х 2 ) и концентрации белковых компонентов рецептурной смеси (х 3 ). Построение системы показателей проводилось в пакете Exсel. Статистические данные по переменным приведены в таблице 2.

Построим матрицу коэффициентов парной корреляции (таблица 3), из которой следует, что потребление корма имеет наиболее тесную связь с концентрацией белковых компонентов рецептурной смеси, а влияние влажности готового продукта и рН среды рецептурной смеси менее существенны. Взаимного влияния рассматриваемых факторов не выявлено, слабых связей факторов математической модели на потребление также не выявлено, поэтому все факторы будут учтены при построении математической модели [5].

Выполнив регрессионный и дисперсионный анализ в пакете Excel, получили зависимости, отраженные в таблицах 4 и 5. Уравнение регрессии зависимости потребления экструдированных пищевых продуктов от рН среды и влажности продукт, концентрации белковых компонентов, имеет вид (1):

у =-0,111-0,113 х 1 -0,031 х 2 +0,027 х 3 (1)

Т а б л и ц а 2

Статистические данные математической модели

у	х 1	х 2	х 3
0,2	7,5	12	55
0,5	6,06	14	65
0,8	6,26	18	77
0,1	6,29	13	53
0,7	6,2	10	65
0,6	6,27	11	65
0,4	6,14	8	55
0,3	6,21	13,5	58
1	6,11	14,5	70
0,9	6,23	18	90

Т а б л и ц а 3

Корреляционная матрица

	у	х 1	х 2	х 3
у	1
х 1	-0,4325	1
х 2	0,4646	-0,1007	1
х 3	0,8356	-0,2985	0,7516	1

Таблица 4

Регрессионная статистика

Множественный R	0,8841
R - квадрат	0,7816
Нормированный R - квадрат	0,6725
Стандартная ошибка	0,17326

В первую очередь рассмотрим зависимости квадратичного вида. Наиболее значимыми переменными в модели являются влажность продукта и концентрация белкой составляющей. Составим соответствующее уравнение регрессии для этих двух факторов при помощи пакета MatСАD.

I := COrder (Nvars , deg)

coeffs := submatriXR , 3 , rows(R) - 1 , 0 , 0)

	( 1  1 )		7.183 x 10 3
	02		- 1.561 x 10 - 3
=	01	coeffs =	0.147
	00		- 4.79
	10		- 0.04
	L 2 0 )		l    - 0.018     ,

Т а б л и ц а 5

Дисперсионная статистика

	df	SS	MS	F
Регрессия	3	0,644875	0,214958	7,160309
Остаток	6	0,180125	0,030021
Итого	9	0,825
	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение
Y-пересечение	-0,1109	1,092108	-0,10155	0,922424
х 1	-0,11278	0,147403	-0,76509	0,473227
х 2	-0,0314	0,027912	-1,12496	0,303585
х 3	0,027395	0,008108	3,37887	0,014879

Таким образом, новое уравнение регрессии имеет вид (2):

у=-0,018 х 2 ²-0,04 х 2 -1,561·10^-3 х 3 ²+0,147 х 3 + (2)

+7,183·10^-3 х 3 х 2 -4,79

В пакете MatСАD представим построенную зависимость потребления корма от влажности готового продукта и концентрации белковых компонентов графически [10-12]. Из графика зависимости представленного на рисунке 11 видно, что функция имеет экстремум.

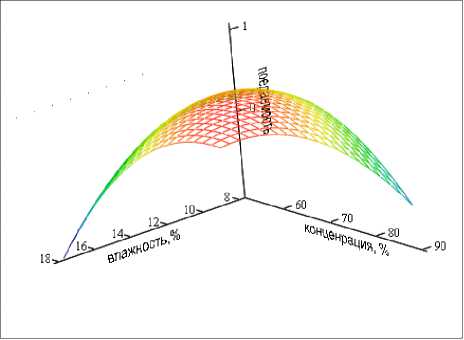
F , (X , Y , Z)

Рисунок 11. Функция зависимости потребления экструдированных пищевых продукто в от влажности и концентрации белковой составляющей

Воспользовавшись критерием Сильвестра найдем критические точки, поскольку наличие экстремума функции вытекает из графика и соответствующего значения квадратичной формы, уравнения (3) и (4). Обозначив через х - концентрацию белковых компонентов, а у – влажность рецептурной смеси, d/dy (0,147х-0,00156х2+0,007183ху- (3)

-0,00у-0,018у2-4,79) =0

d/dx (0,147х-0,00156х2+0,007183ху- (4) 0,00у- (4)0,018у2-4,79)=0

и представляя полученные уравнения для матричного метода в виде

- 0.00312 0.007183^

M :=                       v : =

V 0.007183   - 0.03 6 )

- 0.147

0.04

в МаtCAD, получим учитывая соответствующие матрицы следующее решение:

lsolve(M , v)

82.416 '

15.333.

Из полученного решения, можно сделать вывод о том, что наилучшее потребление экструдированных пищевых продуктов будет при концентрации белковых компонентов 82,4% и влажности 15%.

Моделирование методами нечеткой логики показало наилучшее потребление экструдированных пищевых продуктов при влажности 9% и концентрации белковых составляющих 90%. Расхождение результатов по отношению к концентрации можно признать не значительным. Некоторое несоответствие результатов по влажности можно объяснить тем, что построенная методами математической статистики модель не учитывает влияния других характеристик, например, Ph,

Учитывая близость полученных результатов моделирования можно рекомендовать для взрослых потребителей модели, полученные методами математической статистик, как наиболее простые, а моделирование экструдированных пищевых продуктов для более молодых возрастов производить методами нечеткой логики.

С точки зрения интересов и потребностей общества в наиболее рациональном использовании пищевого сырья, это позволяет повысить уровень ресурсосбережения пищевых производств за счет оптимального использования вторичных пищевых ресурсов.