Оптимизация режимных параметров конденсатора пиролизной биоэнергетической установки для переработки сельскохозяйственных отходов

Особое внимание в современных исследованиях уделяется на выход продуктов пиролиза, поскольку они могут использованы в качестве биотоплива, либо сырья для химического синтеза. Однако выход и качество продуктов пиролиза существенно зависят от эффективности процессов охлаждения и конденсации парогазовой смеси. Именно поэтому оптимизация режимных параметров конденсатора пиролизной установки представляет собой важнейшую инженерную задачу, от решения которой зависит как технологическая, так и экономическая эффективность всей установки [4,5].

По данным ряда авторов, ключевыми параметрами, определяющими интенсивность и полноту конденсации, являются: температура охлаждающей среды, геометрия теплообменных поверхностей, скорость потока парогазовой смеси и материал конденсатора [6,7]. Исследование автора [8] показало, что снижение температуры охлаждающей среды в трубчатом конденсаторе до 12-14°C позволяет увеличить выход жидкой фракции на 1520 % при неизменном составе биомассы.

В обзоре [1] подчеркивается, что успешное масштабирование процессов пиролиза требует не только контроля тепловых условий реактора, но и тонкой настройки систем конденсации, включая температуру, геометрию и скорость охлаждающего потока. Автор указывает, что каскадная схема с последовательным снижением температуры конденсаторов позволяет добиться фракционного разделения жидких продуктов.

Авторы [4] провели численное и экспериментальное исследование конденсации продуктов пиролиза с различными теплообменными конфигурациями. Результаты показали, что эффективность теплообмена существенно зависит от угла потока, площади охлаждения и распределения температуры вдоль поверхности.

Работа [6] использует метод отклика поверхности (RSM) для оптимизации температуры охлаждающей воды. Авторы получили максимальный выход жидкой фазы при температуре 15°C и времени контакта около 4 секунд, что подтверждает важность точной настройки параметров.

Исслодователи [5] моделируют процессы охлаждения пиролизных газов с использованием пакетов ANSYS и COMSOL. В ходе численного эксперимента выявлены предельные параметры температуры стенки, при которых обеспечивается полная конденсация. А авторы [7] исследуют зависимость эффективности конденсации от температуры входной воды. В экспериментальной установке показано, что снижение температуры до 10-12 °C повышает выход жидкой фазы на 20-22 %.

Несмотря на накопленные знания, в современной литературе ощущается дефицит систематизированных подходов к многофакторной оптимизации параметров конденсации с учетом различий в типах биомассы, масштабах установки и целевых продуктах. Отдельного внимания заслуживает применение методов математического моделирования и экспериментального дизайна для нахождения оптимальных режимов.

Целью настоящего исследования является определение оптимальных режимных параметров работы конденсатора-теплообменника с спиральным змеевиком пиролизной установки, обеспечивающих максимальную эффективность теплообмена при минимальном расходе охлаждающей воды.

Материалы и методы. В конструкции конденсатора-теплообменника, используемого в пиролизной биоэнергетической установке, реализована схема герметичного цилиндрического корпуса с размещённым внутри спиральным змеевиком (см. рис. 1). Принцип действия которого основан на охлаждение парогазовой смеси водой, протекающей внутри трубы змеевика в противопоточном направлении к высокотемпературной парогазовой смеси. Геометрические характеристики конструкции представлены в таблицах 1 и 2.

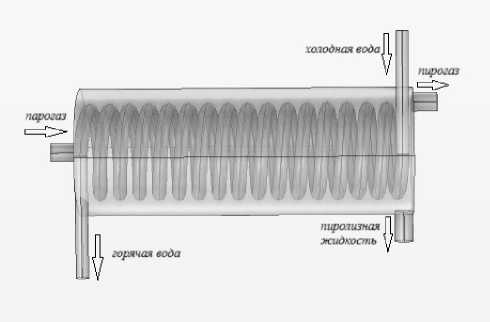
Рисунок 1 - Вид конденсатора-теплообменника ПБЭУ.

Анализ тепловых характеристик системы показал, что температура охлаждающей воды на входе в конденсатор составляет преимущественно 18-20°C, тогда как на выходе, в зависимости от текущих режимов функционирования установки, может возрастать до 50– 70 °C. В то же время температура поступающей парогазовой смеси варьируется в диапазоне 130-200°C, что обуславливает высокий температурный напор и потенциал для эффективного теплообмена.

Таблица 1 - Геометрические параметры спирального змеевика

Параметр	Обозначение	Единицы	Значения
Длина змеевика	L з	м	0,5
Внутренний диаметр змеевика	d звнут	м	0,016
Наружный диаметр змеевика	d звнеш	м	0,022
Толщина стенки	δ	м	0,003
Площадь теплообмена	F з	м²	0,55
Объём змеевика	V з	3 м	0.003
Длина трубы	L тр	м	8
Периметр поперечного сечения	Р з	м	0,05
Площадь сечения канала	F з	2 м	2.01×10-4

Таблица 2 - Геометрические параметры кожуха конденсатора

Параметр	Обозначение	Единицы	Значения
Длина конденсатора	Lк	м	0,5
Внутренний диаметр кожуха	dквнут	м	0,2
Наружный диаметр кожуха	dкнеш	м	0,21
Толщина стенки	δ	м	0,03
Объем кожуха	Vк	м3	0.0157
Площадь межтрубного пространства	Fк	м²	0,0317
Объём свободный	Vсв	м3	0,0127

Теплофизические характеристики воды и ПС приведены в табл.3 и табл.4.

Таблица3 - Теплофизические характеристики охлаждающей воды (в спиральной трубе)

Параметр	Обозначение	Единицы	Значения
Температура на входе	т ех	°C	18-20
Массовый расход	С в	кг/с	0,01-0,05
Плотность	ρ в	кг/м³	998.6-998.2
Теплоёмкость	cp в	Дж/(кг·К)	4190
Теплопроводность	λ в	Вт/(м·К)	0,595–0,598
Динамическая вязкость	М в	Па·с	1,109·103-1,003·103

Таблица 4 - Теплофизические характеристики ПС (в кожухе)

Параметр	Обозначение	Единицы	Значения
Температура на входе	Т пвх	°C	130-200
Плотность	ρ п	кг/м³	1,67-2
Теплоёмкость	cp п	Дж/(кг·К)	1737-1860
Теплопроводность	λ п	Вт/(м·К)	0,05-0,06

Оптимизация режимных характеристик конденсатора ПБЭУ формулируется как задача многокритериальной нелинейной оптимизации, направленной на одновременное достижение высокой эффективности теплопередачи и минимизации расхода охлаждающей воды. Решение данной задачи требует строгого учета термодинамических и гидродинамических закономерностей, отражающих энергетический и массопереносный баланс в системе.

Для оптимизации режимных параметров конденсатора ПБЭУ, предназначенной для переработки органических и сельскохозяйственных отходов, разработана комплексная математическая модель, учитывающая особенности фазового перехода в парогазовой смеси, гидродинамические ограничения и тепловой баланс системы [9].

Модель основывается на энергетическом уравнении для холодного теплоносителя в спиральном змеевике, уравнении Клаузиуса–Клапейрона для определения условий фазового перехода, среднелогарифмическом температурном напоре в противоточной схеме теплообмена, обобщённом коэффициенте теплопередачи, учитывающем тепловые сопротивления и учёте скрытой теплоты конденсации в парогазовой смеси [10].

С учетом фазового превращения компонентов парогазовой смеси, общее количество передаваемой теплоты включает вклад скрытой теплоты конденсации, сопровождающей переход вещества из паровой в жидкую фазу:

Qконд = / rili •ri

где: m , - массовая скорость конденсации компоненты i; r i — её удельная теплота фазового перехода.

Фазовый переход парогазовой смеси в жидкую фазу количественно описывается через условие насыщения, определяемое уравнением Клаузиуса–Клапейрона:

In (-) = -^

VPio'       R v

T вых

-1') Твх

Задача оптимизации формулируется в виде многоцелевой постановки, в рамках которой необходимо одновременно учитывать несколько критериев эффективности. В качестве вектора управляющих переменных рассматривается совокупность параметров:

х = {Gв, Тввх, Gп, Твх }

I

где G в — массовый расход охлаждающей воды, Т ввх — её температура на входе, G п и Т Пвх — соответственно массовый расход и температура парогазовой смеси.

На основе этого вектора формулируются целевые функции, характеризующие теплотехническую эффективность системы и ресурсоёмкость процесса:

f 10) = Ох) =

Q(x)

к(х) • F3 • АТ (х)

что характеризует эффективность теплопередачи, и f ₂⁽х) = G в

отражающая потребление воды.

Сформулированная задача оптимизации предполагает одновременное стремление к максимизации функции f 1(х), характеризующей эффективность теплообмена, и минимизации функции f ₂(х), отражающей ресурсные затраты. С целью упрощения многокритериального анализа и обеспечения взвешенной оценки достигаемого компромисса между этими показателями вводится интегральный функционал:

^Q(x) /О) = -тт-^G в

Функция sО) характеризует интегральную эффективность процесса теплопередачи, тогда как ](х) описывает удельную тепловую отдачу, приходящуюся на единицу расхода охлаждающей воды. Задача оптимизации заключается в одновременном максимизации указанных целевых показателей при условии минимизации водопотребления, что обеспечивает энерго- и ресурсосберегающий режим функционирования конденсационной системы.

Наложенные ограничения обеспечивают физическую реализуемость процесса и гарантируют достижение полной конденсации парогазовой смеси в установившихся теплогидравлических условиях:

Ты < Тас

Т ввых < Т кип

—

-

ЛТ Д

ЬТ без

где: Тнас — температуры насыщения парогазовой смеси; Тнедг — температура недогрева; термогидравлические рамки Re 6 [1900 ...2200], ЛРспир < Л Ртах, а также температурные пределы материалов и отсутствие кипения в спиральном змеевике.

Методологической основой оптимизации режимных параметров конденсатора является многоцелевая байесовская оптимизация, представляющая собой прогрессивный подход к решению задач с высокой вычислительной затратностью и ограниченными экспериментальными возможностями. В отличие от традиционных методов градиентного поиска или полных факторных экспериментов, байесовская оптимизация ориентирована на поиск оптимума при минимальном числе вызовов к целевой функции, что особенно актуально в задачах теплофизического моделирования, требующих значительных вычислительных ресурсов.

Ключевая идея заключается в построении аппроксимирующей модели (суррогата), описывающей поведение целевой функции на основе уже полученных данных (как численных, так и экспериментальных). В качестве такого суррогата, как правило, используется гауссовский процесс, который позволяет не только оценить значение функции,

но и определить уровень неопределенности предсказания в каждой точке параметрического пространства.

На каждой итерации алгоритма выполняется выбор новой точки оценки на основе так называемой функции приобретения — специального критерия, объединяющего знание о текущей аппроксимации функции и её неопределенности. Одним из распространённых критериев является ожидаемое улучшение, которое позволяет сбалансированно учитывать как уже изученные области, так и те, где потенциально может находиться глобальный оптимум.

Этот подход реализуется итеративно: после выбора новой точки производится точный расчёт или экспериментальная оценка целевой функции, далее модель обновляется, уточняя свои предсказания. Такой механизм позволяет эффективно исследовать компромисс между различными целевыми функциями, формируя Парето-оптимальный фронт решений — множество состояний, в которых невозможно улучшить один показатель без ухудшения другого. Таким образом, достигается одновременно максимизация эффективности теплообмена и минимизация расхода охлаждающей воды.

Преимущество метода заключается в том, что он обеспечивает высокую сходимость к оптимуму при минимально необходимом числе итераций, снижая объём как натурных экспериментов, так и ресурсоемких симуляций. Это делает байесовскую оптимизацию особенно ценной в условиях ограниченного экспериментального времени или при высокой стоимости вычислений [11].

Алгоритм байесовской оптимизации режимных параметров КТ ПБЭУ предоставлена на рис.2.

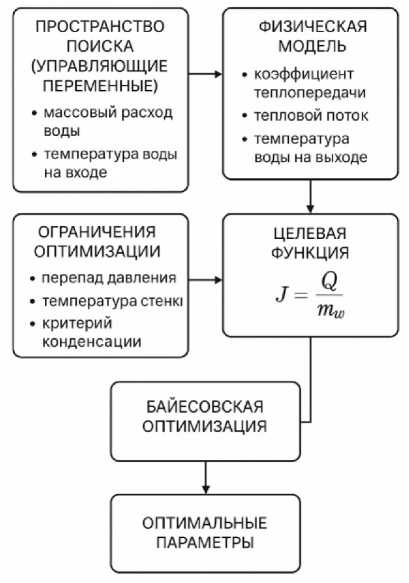
Рисунок 2 - Блок-схема метода байесовской оптимизации.

Программная реализация процесса оптимизации была выполнена на языке Python с использованием библиотеки Scikit-Optimize, предназначенной для реализации вероятностных подходов к глобальной оптимизации. Алгоритм был структурирован в виде последовательного выполнения логически взаимосвязанных этапов, каждый из которых направлен на обеспечение достоверного поиска оптимальных режимных параметров

конденсатора пиролизной установки (рис.3.).

Рисунок 3 - Библиотеки для оптимизации

На первом этапе осуществляется определение пространства управляющих переменных, формирующих основу параметрического поиска (рис.4.). В данную совокупность включены: массовый расход охлаждающей воды, температура воды на входе в теплообменник, температура и скорость поступающей парогазовой смеси, что позволяет охватить ключевые термогидравлические характеристики, влияющие на интенсивность теплообмена и полноту конденсации. space = [ Real(0.01, 0.05, name="m_w"), # кг/с Real(18.0,  20.0,    name="T_w_in"),    # °C

Real(0.05,  0.20,    name="v_pgs"),     # м/с

Real(130.0, 200.0,   name=''T_pgs_in")   # °C

F = 0.55                 # m2 — площадь теплообмена спирали delta = 0.003            # м — толщина стенки lambda_st = 50.0         # Вт/(м-К) - стенка c_pw = 4180.0            # Дж/(кг-К)

Рисунок 4 - Начальные условия

Следующим шагом является формализация физико-математической модели теплообменного процесса в конденсаторе. В рамках данной модели реализованы уравнения теплового баланса, позволяющие рассчитывать интегральный коэффициент теплопередачи (с учётом термических сопротивлений на всех границах фаз), суммарный тепловой поток Q(x), передаваемый от парогазовой среды к охлаждающей воде, температуру выходящей воды, формирующую выходной граничный параметр установки.

Параллельно в модель внедряются физические и конструкционные ограничения, отражающие реальные пределы функционирования системы (рис.5.). К числу таких ограничений относятся максимально допустимый перепад давления на участке теплообменника, температурные пределы стенки змеевика, условие отсутствия кипения в контуре холодного теплоносителя, необходимость полной или частичной конденсации основного компонента парогазовой смеси.

Delta_p_w_max = 2.0е5   # Па

Deltappgsmax = 2.0е4 # Па

T_wall_max = 180.0      # °с def deltapw(mw):     # по модифиц. Дарси-Вейсбах для спирали return 1.0e5*(m_w/0.03)

def delta p_pgs(v pgs): # TODO return 1.0e4*(v_pgs/0.1)

def T_wall_est(k, T_w in, T_w_out, T_pgs_in, T_pgs_out):

• #    оценка температуры стенки

return 0.5*(T_pgs_in+T_pgs_out) - 0.2*(T_w_in+T_w_out)

Рисунок 5 - Граничные условия

В качестве целевой функции используется интегральный критерий эффективности теплообмена J(x) = Q(x)/GB, который позволяет количественно оценивать, насколько эффективно система использует ресурс воды для теплоотвода, что критически важно в условиях ограниченного водоснабжения или при необходимости повышения общей энергоэффективности установки (рис.6.).

Алгоритм байесовской оптимизации в процессе итерационного поиска строит суррогатную модель (гауссовский процесс) на основе ранее вычисленных значений функции J(x), а затем, при помощи функции приобретения, выбирает новую точку в пространстве параметров, в которой ожидается наибольшее улучшение целевого показателя. Такой подход позволяет адаптивно уточнять модель и с минимальными вычислительными затратами приближаться к глобальному оптимуму (рис.7.).

# Запуск байесовской оптимизации res = gp_minimize( func=objectivej dimensions=space, realises, ninitialpoints^lQ, acq_func="Err, random_state=42

Рисунок 6 - Запуск Байесовской оптимизации

• #    Извлечение оптимального результата

Рисунок 7 - Извлечение оптимального результата

Результаты и обсуждение. В результате многократного обновления модели и пересчета критерия полезности формируется набор оптимальных режимных параметров, при которых достигается максимальная интенсивность теплопередачи при минимальном расходе охлаждающей воды. Полученные значения могут быть использованы для настройки реальных установок и служат базой для дальнейшей экспериментальной валидации.

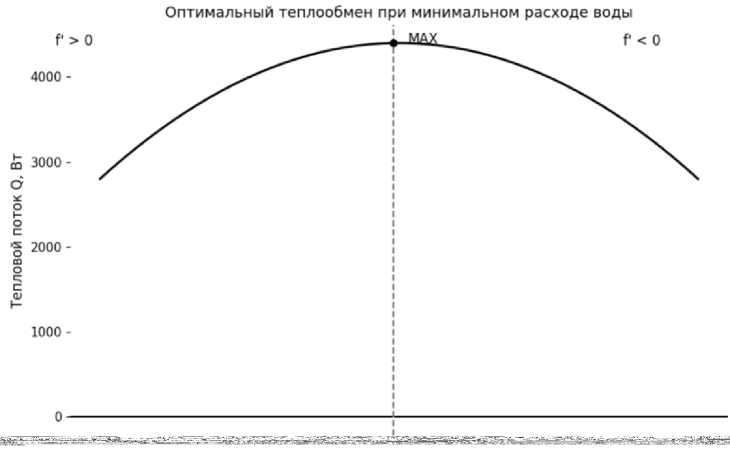
Рисунок 8 - Оптимальный теплообмен при минимальном расходе охлаждающей воды.

Анализ зависимости теплового потока от массового расхода охлаждающей воды (см. рис. 8.) показал наличие характерной параболической формы кривой, что свидетельствует о существовании выраженного экстремума — оптимального режима функционирования теплообменного аппарата. В диапазоне малых значений расхода (до ~0,03 кг/с) наблюдается поступательный рост теплового потока, обусловленный увеличением температурного градиента между парогазовой смесью и охлаждающей водой, а также ростом коэффициента теплопередачи вследствие улучшения условий теплообмена.

Однако по мере достижения критического значения расхода охлаждающей воды (G в ~ 0,03 кг/с), дальнейшее увеличение расхода не приводит к дальнейшему росту эффективности теплообмена. Это объясняется тем, что увеличение скорости потока сокращает время контакта охлаждающей среды со стенкой змеевика, что, в свою очередь, снижает величину среднелогарифмического температурного напора. Таким образом, прирост тепловой мощности становится нивелированным, а в ряде случаев — снижается вследствие неполной реализации температурного потенциала теплоносителя.

Оптимальным с энергетической точки зрения режимом был признан режим с массовым расходом охлаждающей воды порядка G_B = 0,03 кг/с, при котором достигается максимальное значение теплового потока Q(x)~ 4389 Вт. Этот результат указывает на точку технологического равновесия, в которой достигается наибольшая эффективность теплообмена при минимально необходимом расходе ресурса, то есть при оптимальном соотношении между тепловой производительностью системы и затратами охлаждающей воды.

Полученные результаты подтверждают адекватность предложенной физикоматематической модели и высокую применимость метода многоцелевой байесовской оптимизации в задачах настройки режимных параметров теплообменных систем. Совокупность экспериментальных и расчетных данных позволяет утверждать, что предложенный алгоритм обеспечивает поиск эффективных компромиссных решений с учётом многопараметрических ограничений, минимизируя при этом количество необходимых итераций.

Выводы. На основе разработанной физико-математической модели теплообмена в конденсаторе пиролизной установки установлено, что эффективность процесса конденсации продуктов пиролиза критически зависит от сочетания температурных, гидродинамических и фазовых параметров, включая массовый расход охлаждающей воды, начальную температуру теплоносителя и тепловую нагрузку от парогазовой смеси.

Реализация алгоритма многоцелевой байесовской оптимизации в программной среде Python с использованием библиотеки scikit-optimize позволила эффективно сформировать Парето-оптимальный фронт решений. Это дало возможность определить наиболее рациональные режимы работы теплообменного аппарата, обеспечивающие максимальный тепловой поток при минимальном расходе охлаждающей воды.

Результаты численного эксперимента показали наличие выраженного оптимума: при массовом расходе охлаждающей воды G в ~ 0,03 кг/с достигается максимальный тепловой поток Q(x)~ 4389 Вт. Дальнейшее увеличение расхода не приводит к росту эффективности из-за снижения времени теплового контакта и уменьшения температурного напора.

Полученные данные подтверждают применимость многоцелевой байесовской оптимизации в задачах энергетической настройки теплообменного оборудования. Метод обеспечивает высокую точность определения эффективных режимов при минимальном числе расчетных итераций, что особенно актуально в контексте автоматизированного проектирования энергоэффективных пиролизных установок.

Практическая реализация найденных оптимальных параметров может способствовать повышению ресурсо- и энергоэффективности в маломасштабных установках переработки биомассы, включая агропромышленный сектор, а также расширению инструментов цифрового моделирования в задачах проектирования теплотехнических систем.