Оптимизация схемы выведения геостационарного космического аппарата с электроракетной двигательной установкой с использованием ракеты-носителя Falcon-9

Использование электроракетных двигательных установок (ЭРДУ) в качестве маршевых двигателей при реализации космических миссий обеспечивает существенно меньший расход рабочего тела по сравнению с использованием двигателей большой тяги на химическом топливе и, соответственно, доставку на целевую орбиту космического аппарата (КА) большей массы. При этом следует учесть, что применение ЭРДУ приводит к увеличению времени перелета. В данной работе при решении оптимизационной задачи вывода КА на геостационарную орбиту (ГСО) с помощью ЭРДУ

в качестве критерия оптимальности рассматривается конечная масса КА и время перелета на ГСО. Для реализации компромисса между конечной массой КА и длительностью перелета предлагается использовать комбинированную схему перелета на ГСО. Рассматривается схема выведения КА на ГСО с использованием некоторой промежуточной орбиты, имеющей форму эллипса. Для выведения КА на промежуточную орбиту используется ракета-носитель (РН) Falcon 9.

В настоящей работе для решения оптимизационной задачи применяется принцип максимума Понтрягина [2]. Описание деталей используемого подхода представлено в работах [3-9]. Принцип максимума сводит задачу оптимизации к двухточечной краевой задаче. Для решения краевой задачи применяется метод продолжения по пара-

Том 7

метру [3-9]. Для упрощения выбора начального приближения при решении поставленной задачи используется подход, основанный на последовательном получении сначала траектории ограниченной мощности (ОМ) [3; 7] и, после этого, ограниченной тяги (ОТ) [4-6; 8; 9]. При этом начальные значения неизвестных сопряженных переменных, полученные на этапе решения ОМ задачи, используются для начального приближения при решении ОТ задачи [4-6; 8; 9].

1. Математическая модель движения космического аппарата с использованием вспомогательной долготы в качестве независимой переменной центриситет; ex = e∙cos(ω+Ω); ey = e∙sin(ω+Ω); L = v + ω + Ω - истинная долгота; ω - аргумент перицентра; Ω - долгота восходящего узла; μ - гравитационный параметр Земли; i = [ix, iy] – наклонение; ix = tg-cos Q; i у = tg- sin Q a = [ at, ar ,an ] - ускорение КА; at, ar, an - радиальная, трансверсальная и бинормальная компоненты реактивного ускорения соответственно, которые определяются по формулам:

T at = 8 — cos 9 cos v;

m

T ar = 8 sin 9 cosv;             (2)

m

T an = 8—smy,

m

Рассматривается задача оптимизации ОТ траектории. Гравитационное поле предполагается центральным ньютоновским. В данной работе используются дифференциальные уравнения движения в равноденственных элементах [1]. В качестве независимой переменной интегрирования используется вспомогательная долгота K , которая применялась в качестве независимой переменной в работах [7-9]. Уравнения движения принимают вид:

dp   2 p ³

dK  μ q ³

t ;

de _x   p ²

----=---- • dK  μq2

где ϑ, ψ - углы тангажа и рысканья соответственно; T – тяга ЭРДУ КА; c - скорость истечения ЭРДУ; δ - функция включения-выключения двигательной установки КА (δ = 1 - двигатель включен, δ = 0 - двигатель выключен); m - масса КА; t - время. Результатом решения оптимизационной задачи является определение оптимальной программы управления вектором тяги КА – ориентация вектора тяги в пространстве и время включения-выключения двигателей [8; 9].

2. Решение краевой задачи методом продолжения

■          ( q + 1 ) cos L + e x      e y ^

• sin L • a r + ------------------ a t - -²— a n ;

q           q

de _y   p ²

----=---— • dK  μq2

( q + 1 ) sin L + e y      e ^

• ^- cos L • a r +--------------- a t + — a n ;

qq

di _x dK

p ² s ²

2μ q ³

cos L • a n ;

diy dK

ps

3s-? sin L • a n ;

2μ q ³

dL    p ²      dm

K = з ^ • a n ;

dK  μ q ³      dK

8 ( p Y t, ^pp I q ) c’

dt _  1 Г p dK     ( q

Принцип максимума [2; 8] сводит задачу оптимизации к краевой. В данном случае мы получаем двухточечную краевую задачу. При этом граничными условиями будут являться начальные и конечные значения наклонения i , эксцентриситета e , фокального параметра p , отклонения истинной долготы от вспомогательной L_K . Неизвестными параметрами при решении краевой задачи являются 7 начальных значений сопряженных переменных ( p p , p e _x , p e _y , p i _x , p i _y , p L _K ). Последним, седьмым, граничным условием является условие трансверсальности для конечного значения сопряженной к массе переменной p_m . Поэтому краевая задача формулируется с 7 граничными условиями для 7 неизвестных переменных, и начальные условия краевой задачи задаются в виде:

при этом:

s ² = 1 + i X + i² ;

q = 1 + e_x cos L + e_y sin L ;

E = z ' sin L - i , cos L .

xy

В (1) используются следующие обозначения: p - фокальный параметр; e = [ e_x , e_y ] – экс-

p ⁽ K c )= p o ;

e x ⁽ K o )= e x ₀ ; e y ⁽ K o )= e y o ;

X ( ( к o )= xx o ; y ( ( к o )= y o o ;

L K ( ^K o ) = L K o ; m ( ^O ) = m o ,

где K ₀ – некоторое фиксированное значение начальной вспомогательной долготы.

Конечные граничные условия задаются в виде:

p ( K f )= P f ;

e x ( K f ) = e xf ; e y ( K f )= e yf ;

i x ( K f )= i xf ; i y ( K f )= i yf ;

Lk (Kf)=LKf; Pm (Kf ) = 0, где Kf = K0+AK - некоторое фиксированное значение конечной вспомогательной долготы. Нижний индекс «0» обозначает начальные условия, а нижний индекс «f» обозначает конечные условия, K0 и Kf являются заданными значениями вспомогательной долготы в начале и конце перелета соответственно. Краевая задача решается методом продолжения по параметру [3], который сводит краевую задачу к задаче Коши. Дифференциальное уравнение метода продолжения по параметру имеет вид:

dz    ( df

-- — — -- d т    I d z

Если параметр продолжения τ входит в правые части уравнений движения КА, то в этом случае дифференциальное уравнение метода продолжения по параметру принимает вид:

3. Численные примеры

В данной работе в качестве примера использования разработанного метода рассматривается задача расчета многовиткового перелета на ГСО с промежуточной эллиптической орбиты. В качестве критерия оптимизации используется минимизация массы топлива. Число витков траектории предполагается фиксированным. Время перелета оптимизируется. Параметры промежуточной орбиты заданы фиксированными значениями высоты перигея (185 км), наклонения (28,5°), аргумента перицентра (180°), истинной аномалии (0°) и долготы восходящего узла (0°). Параметры промежуточной орбиты и начальная масса КА на этой орбите соответствуют использованию РН Falcon 9 [15]. Для многовиткового перелета c промежуточной орбиты на ГСО с двигателем малой тяги предполагается, что ЭРДУ состоит из 4 однотипных нерегулируемых двигателей СПД-140 с тягой по 280 мН и с удельным импульсом 1780 с. Параметры промежуточной орбиты и масса КА, доставляемая на эти орбиты РН Falcon 9, представлены в табл. 1.

Таблица 1

Масса КА в зависимости от параметров промежуточной орбиты dz dτ

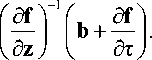
Необходимо найти начальные значения сопряженных переменных z = ( p p , p e _x , p e _y , p i _x , p i _y , p L _K , p m ), при которых выполняются граничные условия рассматриваемой задачи. Для получения решения необходимо интегрировать дифференциальное уравнение метода продолжения по параметру τ от 0 до 1. Для вычисления матрицы частных производных ∆ f /∆ z используется метод комплексного шага [12-14] и функция невязок f имеет следующий вид:

Высота перигея, км	Высота апогея, км	Наклонение, градусы	Начальная масса, кг
185	50000	28,5	4044
185	60000	28,5	3869
185	70000	28,5	3741
185	80000	28,5	3642
185	90000	28,5	3564
185	100000	28,5	3501

f =

P ⁽ K f )^- P f

A

e X ^{( K}f ) - e y f e y (Kf ) - e yf i x ( ^Kf ) - i x f i y ( K f ) - i yf

P l_k ( ^Kf ) - P l_k P m ( K f )

Cистема уравнений оптимального движения [7; 8] численно интегрируется относительно угловой дальности перелета K ∈ [ K ₀; K_f ] с заданными начальными условиями для вычисления функции невязок f .

На рис. 1 представлена вычисленная зависимость конечной массы КА на ГСО и оптимальное время перелета на ГСО с числом витков от 90 до 100 для заданной высоты апогея 50000 км.

S

3460 ^

3450 о

100 витков

99 витков

98 витков

97 витков

96 витков

95 витков

94 витков

93 витков

92 витков

91 витков

100      101      102      103      104      105      106      107      108

Время перелета на ГСО, сутки

Рис. 1. Зависимость конечной массы КА на ГСО от длительности выведения на ГСО при различной угловой дальности перелета

Том 7

При фиксированной высоте апогея промежуточной орбиты 50000 км и угловой дальности перелета 94 витка достигается минимальная длительность перелета (100,3332 суток), при этом на ГСО доставляется КА массой 3507,3098 кг. Для остальных заданных высот апогея промежуточной орбиты также были получены зависимости конечной массы КА на ГСО от длительности выведения. Эти зависимости представлены на рис. 2.

Очевидно, что огибающая представленных на рис. 2 кривых будет представлять собой Парето-фронт задачи максимизации доставляемой на ГСО массы КА и минимизации длительности перелета. Эта огибающая позволяет определить оптимальные значения высоты апогея промежуточной орбиты и оптимальное число витков, которые для каждой длительности перелета обеспечивают доставку на ГСО КА максимальной массы. Зависимость оптимального времени пере-

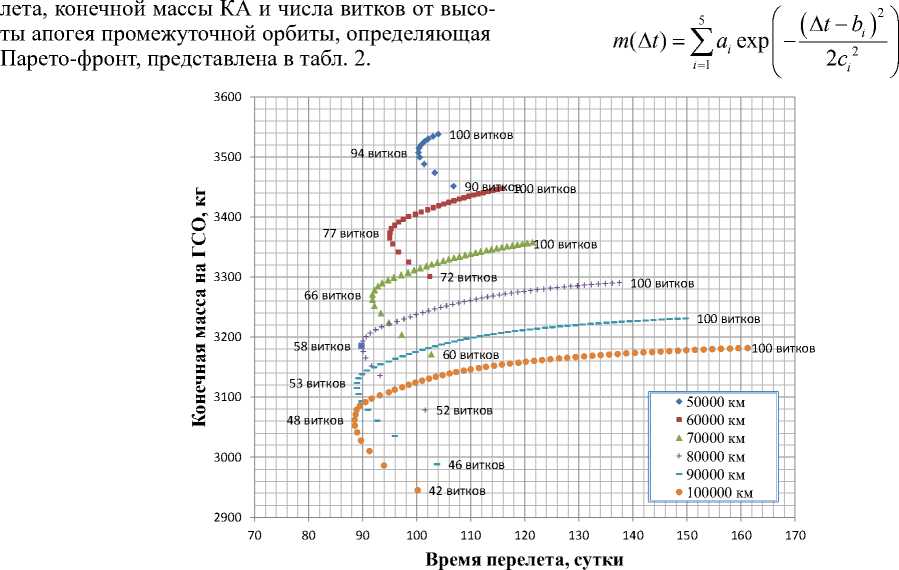
Для оценки оптимальных значений высоты апогея, оптимальных значений числа витков и значений конечной массы КА в промежутках между вычисленными длительностями перелета используется интерполяция данных из табл. 2 B -сплайнами. Выводятся функция Гаусса высшего порядка (8)-(10) для оценки этих величин, а в табл. 3-5 указаны значения используемых в этих формулах значения коэффициентов a_i , b_i , c_i .

ra (A t) = E ai exP i=1

-

к

^(A t - b i )   .

2 c-

’ )

N rev ^{( A} t ) = E a i exP —

i = 1

( A t - b ) ²

2 ^²

;

.

Рис. 2. Зависимость массы КА на ГСО от длительности выведения на ГСО с различными высотами апогея

Зависимость оптимального времени перелета, конечной массы КА и числа витков от высоты апогея промежуточной орбиты

Таблица 2

Высота апогея, км	Время перелета, сутки	Конечная масса, кг	Число витков
50000	100,3332505	3507,309821	94
60000	95,04643895	3373,430022	77
70000	91,80151375	3270,957328	66
80000	89,80805343	3185,700842	58
90000	88,96042273	3123,891598	53
100000	88,51588761	3062,320214	48

Таблица 3

Значения коэффициентов для интерполяции оптимального радиуса апогея

коэффициент	i = 1	i = 2	i = 3	i = 4	i = 5	i = 6	i = 7
a i	1,52e+05	848,5	-175,7	6,095e+04	2256	176,4	4,43e+04
b i	85,34	89,78	89,66	80,31	106,1	94,95	106,5
c i	2,186	0,8258	0,887	13,07	4,009	4,196	60,08

Таблица 4

Значения коэффициентов для интерполяции оптимального числа витков

коэффициент	i = 1	i = 2	i = 3	i = 4	i = 5	i = 6
a i	83,42	94,23	-21,81	25,14	0,01428	7,028
b i	103,1	95,26	95,24	89,33	93,34	88,55
c i	4,645	5,259	3,292	2,869	0,01916	1,318

Таблица 5

Значения коэффициентов для интерполяции конечной массы КА

коэффициент	i = 1	i = 2	i = 3	i = 4	i = 5
a i	3579	533,3	165,9	37,32	158,1
b i	105,1	89,62	88,24	88,6	95,27
c i	25,37	4,879	2,539	1,076	4,61

Зависимости оптимальных значений высо- и значений конечной массы КА от продолжитель-ты апогея, оптимальных значений числа витков ности перелета на интервале от 88,516 суток до

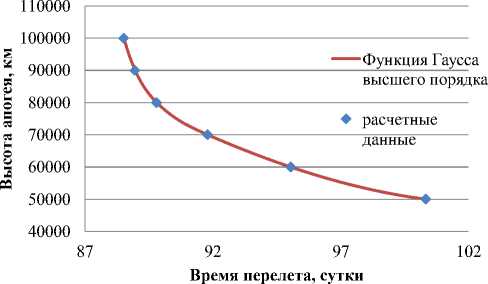
Рис. 3. Зависимость оптимальных значении высоты апогея от длительности выведения на ГСО

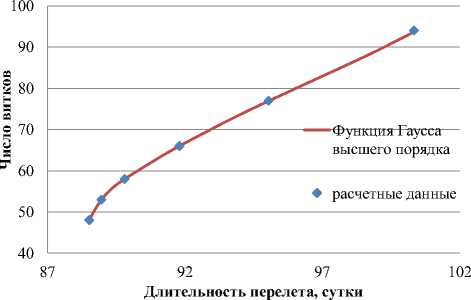
Рис. 4. Зависимость оптимального числа витков от длительности выведения на ГСО

Том 7

100,333 суток, вычисленные по (8)-(10), представлены на рис. 3-5.

На рис. 6 и 7 представлены виды оптимальной ОТ траектории перелета c заданных

промежуточных орбит (высота перигея

высота апогея

185 км,

50000 км, 60000 км, 70000 км,

80000 км, 90000 км, 100000 км, наклонение - 28,5°) на ГСО.

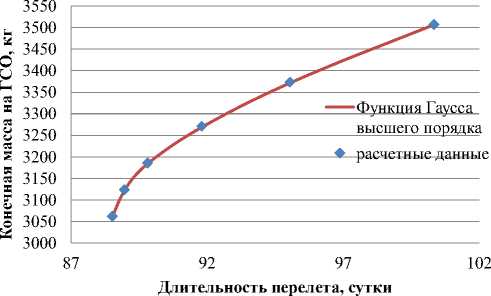
Рис. 5. Зависимость конечной массы КА на ГСО от длительности перелета

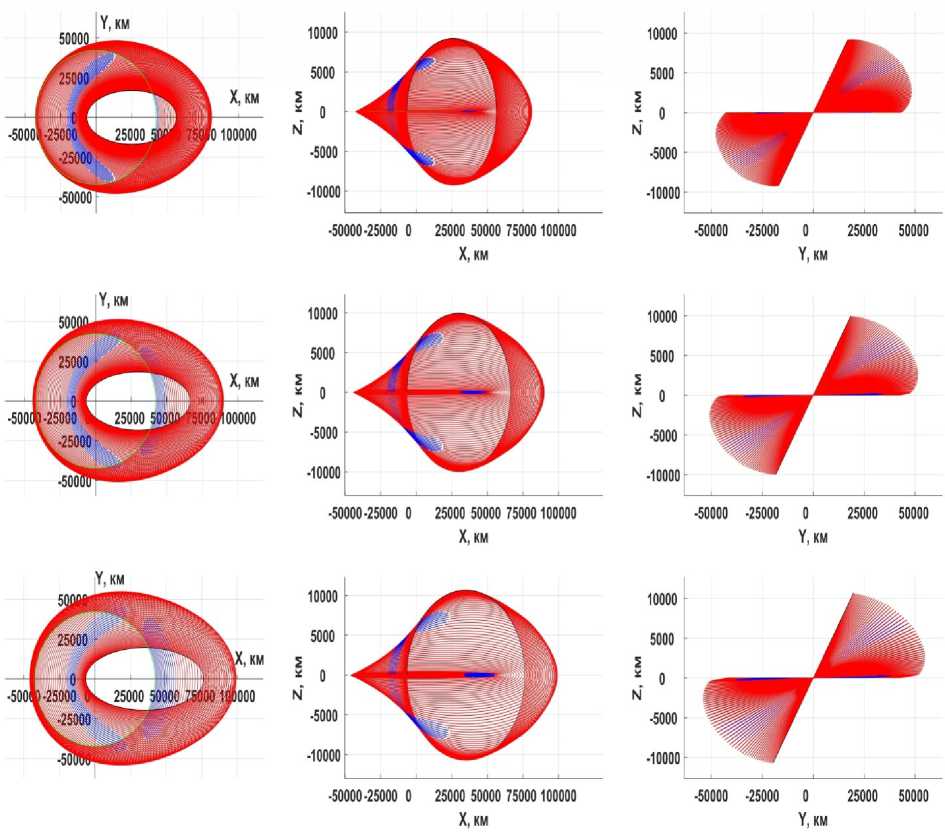
Рис. 6. Проекции оптимальных траекторий на координатные плоскости: верхний ряд – 94 витковые ОТ траектории с начальной высотой апогея 50000 км, средний ряд – 77 витковые ОТ траектории с начальной высотой апогея 60000 км, нижний ряд – 66 витковые ОТ траектории с начальной высотой апогея 70000 км

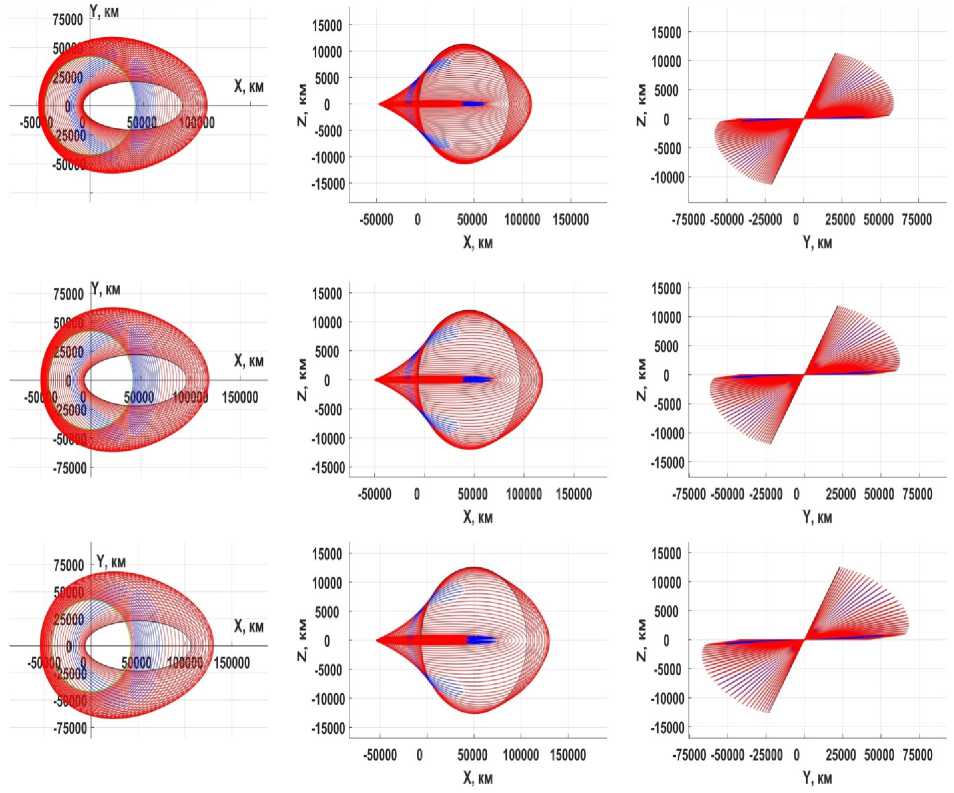
Рис. 7. Проекции оптимальных траекторий на координатные плоскости: верхний ряд – 58 витковые ОТ траектории с начальной высотой апогея 80000 км, средний ряд – 53 витковые ОТ траектории с начальной высотой апогея 90000 км, нижний ряд – 48 витковые ОТ траектории с начальной высотой апогея 100000 км

Заключение

В работе рассмотрена задача оптимизации межорбитального перелета КА с ЭРДУ на ГСО. Запуск осуществлялся с космодрома на мысе Канаверал с помощью ракеты-носителя Falcon 9. Рассмотрена комбинированная схема выведения с использованием промежуточной эллиптической орбиты. Перелет на геостационарную орбиту после отделения КА от ракеты-носителя осуществляется с использованием электроракетной двигательной установки с 4 однотипными нерегулируемыми двигателями СПД-140.

Рассмотрена задача оптимизации многовит-кового перелета между орбитами КА с двигателем

ОМ и ОТ. Результаты решения ОМ задачи используются в качестве начальных приближений для сопряженных переменных при решении ОТ задачи. Для решения задачи оптимизации используется принцип максимума Понтрягина, относящийся к непрямым методам. Принцип максимума свел задачу оптимального управления к двухточечной краевой задаче для системы обыкновенных дифференциальных уравнений. Полученная краевая задача решалась методом продолжения по параметру, который сводил краевую задачу к задаче Коши.

Представлены полученные оценки максимальной конечной массы КА при выведении КА на ГСО с использованием маршевой ЭРДУ с гео-переходных орбит, обеспечиваемых РН Falcon 9.