Оптимизация состава оборудования гибридных энергетических систем с возобновляемыми источниками энергии

Одной из наиболее востребованных и активно развивающихся технологий производства электрической энергии в настоящее время являются гибридные энергетические системы с возобновляемыми источниками энергии (hybrid renewable energy systems – HRES) [1, 2].

Первоочередной областью практического применения HRES является электроснабжение потребителей, территориально расположенных в труднодоступных районах, удаленных от центральной электрической сети. Огромные территории с плохо развитой транспортной инфраструктурой и низкая плотность населения определяют хорошие перспективы практического применения HRES в России. По оценкам Минэнерго РФ потенциал для малой генерации насчитывает около 100 тыс. небольших изолированных поселений по всей территории России, в том числе в ряде районов Крайнего Севера и Дальнего Востока, где обеспечить централизованное энергоснабжение невозможно по техническим и экономическим причинам [3]. Велик потенциал развития малой генерации на объектах инфраструктуры Северного морского пути, объектов Министерства обороны РФ, Министерства природных ресурсов и др. Это энергоснабжение метеорологических станций, маяков, военной техники, судового оборудования, объектов сотовой связи, рыбацких хозяйств, кемпингов, технологических потребителей нефте- и газопроводов [4].

В общем случае в составе HRES могут использоваться генерирующие источники различной физической природы, однако наибольшее распространение получили HRES на основе фотоэлектрических (photovoltaic – PV) и ветроэнергетических установок (wind turbines – WT) [5]. Объясняется это тем, что энергия ветра и солнечного излучения являются наиболее доступными видами энергии, энергетические установки на их основе выпускаются на широкий диапазон мощностей и их можно максимально приблизить к потребителям электроэнергии, что особенно важно для автономной энергетики. Для сглаживания баланса мощностей в составе большинства автономных HRES применяются накопители энергии на основе аккумуляторных батарей (battery bank – BB) и/или топливных элементов (fuel cell – FC), в качестве гарантированного источника питания чаще всего применяются дизель-генераторные установки (DG).

HRES могут значительно различаться по установленной мощности, типу и количеству генерирующих источников, архитектуре построения, алгоритмам управления режимами и т. п. [1, 5, 6]. При этом неизменной и важной задачей проектирования любой HRES является выбор состава основного энергетического оборудования, при котором будут обеспечены необходимая надежность энергетической системы и хорошие техникоэкономические показатели. Стохастический характер первичных энергоносителей и нелинейность характеристик генерирующих источников определяют высокую сложность решения данной проблемы, которая с математической точки зрения формулируется как оптимизационная задача.

Решению задач оптимизации состава оборудования HRES в последнее время посвящено большое количество научных работ, авторы которых используют разнообразные критерии и алгоритмы оптимизации, применяют и разрабатывают различные модели компонентов HRES [7, 8]. Проведенный обзор современных научных работ, посвященных оптимизации состава оборудования HRES, показал, что основными проблемами решения данной задачи являются достоверное прогнозирование мощности, генерируемой установками возобновляемой энергетики, и выбор алгоритма решения оптимизационной задачи, обеспечивающего надежное определение экстремума целевой функции при заданных ограничениях с минимальными временными затратами. Применение разнообразных приемов и способов достижения цели исследований свидетельствует о том, что на сегодняшний день научная проблема оптимизации состава оборудования HRES остается актуальной и не имеет законченного решения.

Цель настоящей работы состояла в разработке методики оптимизации состава оборудования HRES, обеспечивающей ее практическое применение для выбора оборудования энергетических систем, территориально расположенных в любом регионе России. Необходимость создания такой методики отмечается авторами работ [9, 10], посвященных решению аналогичных научно-исследовательских задач. Отличительной особенностью разработанной методики является использование для прогнозирования солнечной радиации оригинальной модели на базе данных Национального управления по аэронавтике и исследованию космического пространства (National Aeronautics and Space Administration – NASA) [11] и применение функции обратного распределения Вейбулла для прогнозирования суточного хода скорости ветра.

Предлагаемая методика построена на основе алгоритма роя частиц (particle swarm optimization –

PSO), который является одним из самых распространенных для решения задач оптимизации HRES [12–14]. Результаты сравнения алгоритма PSO с другими видами алгоритмов при решении задач оптимизации состава оборудования HRES доказывают его высокую производительность [2, 15–17], а также надежное функционирование при использовании различных целевых функций и ограничений [18].

В качестве основного инструмента при проведении исследований использовался программный комплекс MATLAB, в котором и реализована математическая модель оптимизационной задачи.

Формирование временных рядов данных

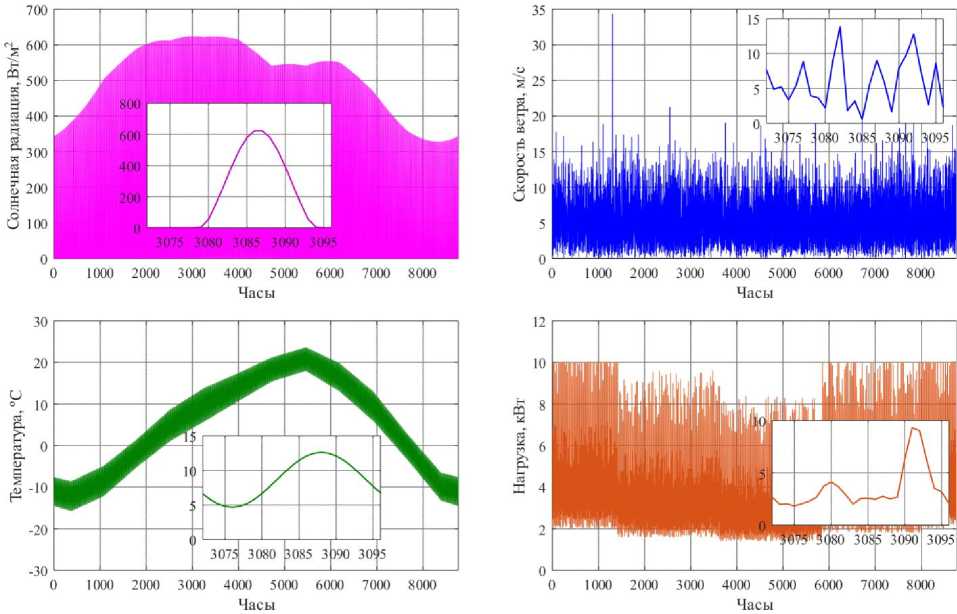
Так как режимы работы HRES определяются соотношением мощностей, генерируемой источниками энергии и потребляемой нагрузкой, для их моделирования необходимо сформировать временные ряды климатических данных и графика нагрузки потребителя. Климатические ряды данных формируются на основе географических координат размещения HRES и данных многолетних наблюдений ближайшей метеостанции, для построения графика электрических нагрузок используются имеющиеся данные об объекте электроснабжения.

В настоящей работе для построения временного ряда солнечной радиации G ( t ) используется комбинированная модель, в которой часть параметров рассчитывается по аналитическим выражениям, а часть определяется с помощью эмпирических коэффициентов, полученных из базы данных NASA [11] для заданной в расчетах географической точки размещения солнечной батареи (СБ). Суммарная солнечная радиация, поступающая на поверхность СБ, определяется по выражению

G = (Gh -Gdh)■+ cos 9 z

_       . cos 9 _Z1 . 1 + 1 + cos P)

• + GDH ■ Ai—^ + (1- 4)'|—+ cos 9 zV

• 1    - cos в

• + GH ■P2---,

где G H , G DH – значения суммарной и рассеянной солнечной радиации, поступающей на горизонтальную поверхность, соответственно, Вт/м²; θ – угол между направлением потока солнечного излучения к поверхности и нормалью к ней, рад; θ _z – зенитный угол Солнца, рад; ρ – альбедо земной поверхности; β – угол наклона приемной площадки к горизонтальной плоскости, рад; A_i – показатель анизотропии, который определяется по уравнению

A i = G     G - ,                                 (2)

G ₀

где G 0 = 1367 Вт/м² – внеатмосферная радиация на горизонтальную поверхность.

Используемая в настоящих исследованиях модель солнечной радиации подробно описана в работе [11]. Особенностью модели является использование в качестве исходных данных численных значений индекса прозрачности атмосферы и альбедо поверхности, полученных из базы данных NASA. Это позволяет использовать модель для прогнозирования основных характеристик солнечного излучения в любой географической точке России, в том числе и для территорий, по которым отсутствуют результаты регулярных актинометрических наблюдений.

Для построения временного ряда скоростей ветра V ( t ) экспериментальные данные о скорости ветра аппроксимируются стандартной функцией распределения Вейбулла:

• ( V ) k

F(V ) = 1 - e I c ^ , (3) где с – параметр масштаба; k – параметр формы; F ( V ) – функция интегральной повторяемости скорости ветра.

С помощью известных методов статистической обработки экспериментальных данных, подробно представленных в [19], предварительно определяются значения коэффициентов с и k для каждого месяца года, и на их основе формируется временной ряд скоростей ветра для необходимого промежутка времени согласно распределению

V ( t ) = c •[- In ( 1 - F(V ) ) ] k (4)

Результаты предварительно проведенных исследований показали, что использование функции обратного распределения Вейбулла (4) позволяет значительно повысить достоверность прогнозирования выработки электроэнергии WT на суточных временных интервалах.

Для построения временного ряда температуры воздуха Т ( t ) используется модель суточного хода температуры [20], согласно которой

T ( t ) = T + 0,5 A T ■ cos [ 2 П ■ ( t мест - t max )/ t пер ] , (5)

где T – среднесуточная температура воздуха, °С; ∆Т – суточная амплитуда температуры воздуха, °С; t_пер – период изменения температуры воздуха, ч; t _max – местное время максимума температуры, ч; t мест – локальное (местное) солнечное время, ч.

Модель суточного хода температуры применима для любого дня года и любого населенного пункта, а ее применение обосновано тем, что изменения температуры в северных широтах имеют явно выраженный суточный ход, учет которого позволяет повысить точность прогнозирования выработки электроэнергии PV.

Для построения временного ряда графика электрических нагрузок используется вероятностно - статистическая модель электрических нагрузок децентрализованного потребителя [21]:

P oad ( t) = P ik • ks k ±P^ P ik ), (6)

где P load ( t ) – расчетная активная электрическая нагрузка, Вт; P_ik – математическое ожидание активной нагрузки i - го часа k - го сезона (определяется по статистическим графикам), Вт; k Sk – коэффици ент сезонности; g( P ik ) - среднее квадратичное отклонение; β – коэффициент надежности расчета (при вероятности 0,975 β = 2).

Используемая в данной работе вероятностностатистическая модель позволяет получить достаточно точный детальный прогноз режимов потребления электрической энергии для конкретного объекта электроснабжения со специфическими для него особенностями.

Временные ряды данных формируются на первом этапе исследований, сохраняются в виде .mat файлов и используются в дальнейшем для моделирования рабочих режимов HRES. Такая организация вычислений позволяет значительно снизить требования к вычислительным ресурсам компьютера, а также обеспечивает возможность решения оптимизационной задачи с различными критериями оптимизации и ограничениями.

Модели компонентов

Для решения задач оптимизации состава оборудования HRES преимущественно используются упрощенные «энергетические» модели компонен- тов, однозначно связывающие их выходные энергетические характеристики с внешними факторами и входными воздействиями [12, 14, 17].

В настоящей работе для определения выходной электрической мощности СБ используется следующее выражение [20]:

P pv = C ff ■ ^ FM ■ n_con v ■ G ■ ln(10⁶ ■ G )/ T fm , Вт, (7) где N FM – число фотоэлектрических модулей (ФМ) в СБ; C FF – постоянный коэффициент СБ; η conv – КПД преобразователя с контроллером максимальной мощности; G – текущий уровень солнечной радиации, Вт/м²; Т _FM – текущая температура ФМ, К.

Численные значения коэффициента CFF опре- деляются по уравнению cff =

FF ■ T ef ------ref X

^G ref

^[ I SC ⁺ k I⁽ T FM   T re^H V OC ⁺ k V⁽ T FM   T ref^{) ]}   zo\

^X                           a                            , ⁽⁸⁾

ln(10⁶ ■ G ref )

где FF – коэффициент заполнения вольт-амперной характеристики (ВАХ) ФМ; T ref , G ref – значения температуры и освещенности ФМ при стандартных условиях; k _I, k _V – температурные коэффициенты тока короткого замыкания и напряжения холостого хода ФМ соответственно.

Коэффициент заполнения ВАХ ФМ определяется по данным их технической спецификации:

^FF = I MPP ■ V MPP I S SC ■ V OC ,                 ⁽⁹⁾

где IMPP, VMPP – паспортные значения тока и на- пряжения ФМ в точке максимальной мощности; ISC, VOC – паспортные значения тока короткого замыкания и напряжения холостого хода ФМ при стандартных условиях тестирования.

Для определения температуры поверхности ФМ используется эмпирическое выражение, полученное по результатам статистической обработки экспериментальных данных, полученных в условиях эксплуатации кремниевых ФМ в Сибири [20]:

T FM = T + 0,0283 - G - 0,0058 - G - V +

+ 0,0005 - G - V ², ° C,

где Т – температура окружающего воздуха, °С; V – скорость ветра, м/с; G – текущий уровень солнечной радиации, Вт/м².

Нужно отметить, что многие авторы в своих исследованиях принимают температуру поверхности ФМ, равной температуре окружающего воздуха, что обуславливает заметное снижение точности расчетов при определении выходной электрической мощности СБ. Результаты эксплуатации фотоэлектрических станций показывают, что превышение температуры ФМ над температурой внешней среды при высоких значениях солнечной инсоляции может достигать 30 °С, поэтому учет реальной температуры ФМ в эксплуатационных условиях позволяет существенно повысить достоверность результатов при определении выходной мощности СБ P _PV.

Выходная электрическая мощность WT определяется скоростью ветра, набегающего на ветро-колесо, и рабочей характеристикой, заявленной ее производителем. В настоящей работе для определения выходной мощности WT используется распространенная «кубическая» аппроксимация рабочей характеристики [12, 14]:

"0 V (1 ⁺i) T , (19) (1 + i) T -1

где i – процентная ставка; Т – общий срок службы энергетической системы.

С учетом того, что срок службы отдельных компонентов HRES может быть разным, их необ- ходимо привести к условиям единовременного платежа. В большинстве практических случаев наименьший срок службы из всех компонентов энергетической системы имеют аккумуляторные батареи. Например, если значение жизненного цикла HRES принято равным Т = 20 лет, а срок службы ВВ составляет 5 лет, для определения приведенной стоимости ВВ CВВ необходимо ис- пользовать следующее выражение

CBB = CBB_0 ■ I ^{1 +}

++). (1 + i )5   (1 + i )¹⁰   (1 + i )¹⁵J

где CВВ_0 – первоначальная цена ВВ, долл.

Для дизель-генераторных установок, срок службы которых определяется по количеству мото- часов до капитального ремонта, приведенная стоимость рассчитывается по аналогичной (20) формуле после определения их срока службы по уравнению

Tdg = HOV, лет, (21)

HF где HF – количество часов работы DG в год, рассчитанное по результатам моделирования; HOV – количество моточасов до капитального ремонта, заявленное производителем DG.

Для HRES в конфигурации PV-WT-BB-DG суммарные приведенные капитальные затраты определяются по уравнению

Cap = CRF x

^x(NWT ■ CWT ⁺NPV ■ CPV ⁺NBB ■ CBB ⁺CDG ⁺Cinv ), ⁽²²⁾ где NWT, CWT – количество и стоимость WT; NPV, C_PV – количество и стоимость PV; N_BB, C_BB – количество и приведенная стоимость BB; C_DG – приведенная стоимость DG; C_inv – приведенная стоимость инвертора.

Пренебрегая затратами на обслуживание инвертора, суммарные затраты на техническое обслуживание HRES определяются по уравнению

Main = NWT ■ MWT + N_PV■ M_PV+

⁺NBB ■ MBB ^{+ M}DG ^{+ M}fuel,              ⁽²³⁾

где MWT, MPV, MBB, MDG – ежегодные затраты на техническое обслуживание WT, PV, BB и DG; Mfuel – затраты на дизельное топливо, рассчитанные по результатам моделирования.

В качестве технических ограничений используются требования к надежности, которые в данной работе задаются в виде численного значения требуемого показателя вероятности потери питания (loss of power supply probability – LPSP*). Для обеспечения требуемого уровня надежности HRES должно выполняться следующее условие

LPSP < LPSP*,                        (24)

где LPSP – расчетная величина вероятности потери питания, которая определяется в результате моделирования режимов HRES по уравнению

T

Z LPS( t)

LPSP = -t=1-------,                        (25)

Z ^Pload( t)

t=1

где LPS(t) соответствует энергии, потребленной нагрузкой на временных интервалах, в которых остаточная емкость ВВ ниже минимально допустимого значения:

LPS( t) = ^(t) - Ppv (t) - P_Wt (t) -^ηinv

- SOC( t -1) ■ (1 -a) - SOCminl ■ nch.         (26)

Горизонт моделирования режимов HRES в данной работе принят в один год, соответственно в уравнении (25) Т = 8760.

Для оптимизационной задачи ограничениями также являются минимальное и максимальное количество ФМ в СБ NPV, количество ветроэнергетических установок NWT, число аккумуляторов в аккумуляторной батарее NBB. Для конфигурации HRES с DG минимальное количество энергетического оборудования принимается равным нулю, для HRES без гарантированного источника питания минимальная емкость ВВ QBB (кВт∙ч) определяется с учетом требований к автономности, которая выражается в числе часов питания ТBB (ч) потребителей от ВВ при отсутствии генерации от возобновляемых источников, допустимой глубины разряда DOD батарей, общей эффективности сис- темы хранения энергии:

Ea ■ Trr Or_R > ------^L--BB-----,

^^B 24 ■ DOD ■ n_ch■ n_mv

где EL – значение среднесуточной величины энергии (кВт∙ч), потребляемой нагрузкой в месяц года с самым высоким значением коэффициента сезонности kSk.

Алгоритм роя частиц

Алгоритм PSO был разработан Джеймсом Кеннеди и Расселом Эберхартом в 1995 году и представляет собой метод оптимизации нелинейных функций, основанный на природном поведении стай птиц [23]. Идея алгоритма заключается в непрерывном перемещении частиц в возможном пространстве решений, при этом текущее состояние частицы характеризуется двумя переменными: координатой x_i^k и скоростью перемещения v_i^k .

В процессе расчета направление и вектор скорости каждой из частиц изменяются в соответствии со сведениями о найденных на предыдущей итерации оптимумах: Ppbest_i – оптимальное значение целевой функции из всех точек, в которых побывала данная частица; Pgbest – оптимальное значение целевой функции, найденное всеми частицами.

В практических приложениях большее распространение получил модифицированный алгоритм, предложенный Юхи Ши и Расселом Эберхартом в 1998 году [24], в котором в отличие от классического используется дополнительный коэффициент инерции w, который определяет градиент изменения скорости частиц. Модифицированный алгоритм PSO описывается следующей системой уравнений:

• vk⁺¹= vk ■ w+cl ■ rl ■ [ Ppbesti - xk ]+

• +c2 ■ r  Pgbest - xk ];

• xk⁺¹= xk + vk;                               (28)

i = 1, 2, ...., ^;

• k=1, 2, ..., k_max ,

где с1, с2 – константы ускорения; r1, r2 – случайные функции в диапазоне [0,1]; i – порядковый номер частицы; k – значение текущей итерации; N – число частиц роя; kmax – максимальное число итераций.

В данной работе используются численные значения и законы изменения коэффициентов инерции и ускорения, установленные в работе [25]. Число частиц роя и максимальное число итераций алгоритма выбираются в соответствии с размерностью решаемой задачи. Предварительно проведенные вычислительные эксперименты показали, что для рассматриваемого ниже примера рациональными значениями являются: N = 80, kmax = 100.

Результаты оптимизации

Для апробации предлагаемой методики рассмотрен пример выбора состава оборудования HRES, предназначенной для электроснабжения изолированного потребителя с максимальной мощностью нагрузки 10 кВт, территориально расположенного в районе г. Владивостока (43°6' с.ш., 135°42' в.д.). Сформированные временные климатические ряды и годовой график нагрузки потребителя представлены на рис. 3.

Для построения временного ряда солнечной радиации, приходящей на горизонтальную поверхность в г. Владивосток, использовались данные NASA за 22-летний период наблюдений, временные ряды скорости ветра и температуры воздуха построены по данным сайта «Расписание погоды» [26] за 15-летний период наблюдений по метеостанции № 31960. График электрических нагрузок построен на основе типового графика нагрузок коммунальнобытового потребителя, коэффициент сезонности изменяется от 0,7 в летние месяцы до 1 в зимние месяцы года. На каждом из графиков, представленных на рис. 3, наложены суточные тренды изменения соответствующих параметров для дня 9 мая.

Рис. 3. Временные ряды климатических данных и график нагрузки потребителя

энергетических

В качестве основного энергетического оборудования HRES использовались следующие виды компонентов: фотоэлектрические модули поли-кристаллического типа Kyocera Solar KD320GX-LPB, ветроэнергетическая установка AeolosH2KW, аккумуляторы HOPPECKE 8 OPzS 800, дизель-генераторная установка Perkins 403D-15G, автономные инверторы Victron Phoenix3000 суммарной мощностью 12 кВт. Технические характеристики компонентов приняты в соответствии с данными технической спецификации их производителей, экономические показатели определены по данным работ [15, 27, 28]. Основные техникоэкономические характеристики основного оборудования HRES представлены в табл. 1.

Приведенные в табл. 1 экономические характеристики оборудования включают затраты на монтажные, пусконаладочные работы и соответствующие преобразователи для PV, WT и BB. Процентная ставка в расчетах принята равной i = 7 %, срок жизненного цикла проекта Т = 20 лет. Солнечная батарея установлена неподвижно под углом 43° к поверхности и ориентирована на юг, расход дизельного топлива при номинальной нагрузке DG составляет 3,67 литра, стоимость топлива принята равной $0,67/литр. Допустимая глубина разряда аккумуляторных батарей принята равной DOD = 70 %, максимальная зарядная мощность Pch.max = 0,2∙SOCmax.

Искомыми переменными оптимизационной задачи является число единиц оборудования HRES: количество фотоэлектрических модулей N_PV, ветроэнергетических установок N_WT и аккумуляторов N_BB в аккумуляторной батарее. Критерием оптимизации является минимальная стоимость жизненного цикла LCC = min. Задачи исследований состояли в определении оптимального состава оборудования HRES различных конфигураций.

В табл. 2 представлены результаты решения задач оптимизации состава оборудования HRES с гарантированным источником питания в виде DG.

Результаты исследований показывают, что при принятых в данной работе технико-экономических характеристиках оборудования минимальные общие затраты на энергетическую систему в течение всего ее срока службы соответствуют конфигурации с применением фотоэлектрических и ветроэнергетических установок. В сравнении с энергетической системой, построенной на базе одного DG, стоимость жизненного цикла такой системы уменьшается практически в 1,4 раза. Структура затрат на лучшую конфигурацию HRES с DG показана на рис. 4.

Важными достоинствами DG-PV-WT-BB конфигурации HRES являются высокая надежность и хорошие экологические характеристики, обеспечиваемые на счет значительного сокращения часов работы DG: расчетное число моточасов DG в данной конфигурации составляет 742 часа в год, при общем расходе топлива 1123 литра. Временные диаграммы рабочих режимов оборудования HRES на 48-часовом временном интервале (для дней 22–23 февраля), построенные по результатам моделирования, показаны на рис. 5. Для наглядного отображения всех переменных на одном графике для показателя SOC использовался масштабирующий коэффициент 1/4.

Анализ временных диаграмм, представленных на рис. 5, показывает, что режимы работы HRES полностью соответствуют принципам управления, описанным выше. Возможность построения и изучения временных диаграмм для произвольных интервалов времени является важным достоинством предлагаемой методики. Применение данной опции позволяет использовать разработанное программное обеспечение не только для оптимизации

Таблица 1

Технико-экономические характеристики оборудования

Показатель	Оборудование
	Kyocera Solar KD320GX-LPB	Aeolos H2KW	HOPPECKE 8OPzS 800	Perkins 403D-15G	Victron Phoenix3000
Номинальная мощность (емкость)	320 Вт	2 кВт	1,6 кВт∙ч	12 кВт	12 кВт
Капитальные затраты, долл. США	800	4200	360	10 000	8600
Затраты на обслуживание, долл. США	8	170	3,6	0,33/ч	0
Срок службы	20 лет	20 лет	5 лет	15 000 ч	10 лет

Таблица 2

Оптимальный состав оборудования HRES с гарантированным источником питания

Конфигурация HRES	Количество единиц оборудования				LCC, долл. США
	NPV	NWT	NBB	NDG
DG	0	0	0	1	20 046
DG-PV-BB	86	0	73	1	17 044
DG-WT-BB	0	14	40	1	16 310
DG-PV-WT-BB	39	8	38	1	14 428

Таблица 3

Оптимальный состав оборудования HRES без гарантированного источника питания

LPSP*, %	Количество единиц оборудования				LCC, долл. США
	NPV	NWT	NBB	NDG
2	51	9	39	0	14 146
1	53	9	42	0	14 588
0	79	4	63	0	15 846

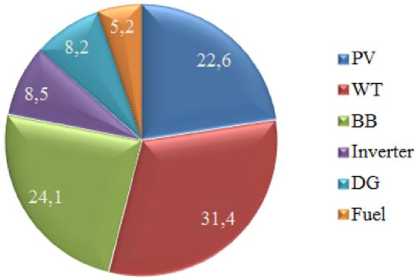
Рис. 4. Структура общих затрат на гибридную энергетическую систему

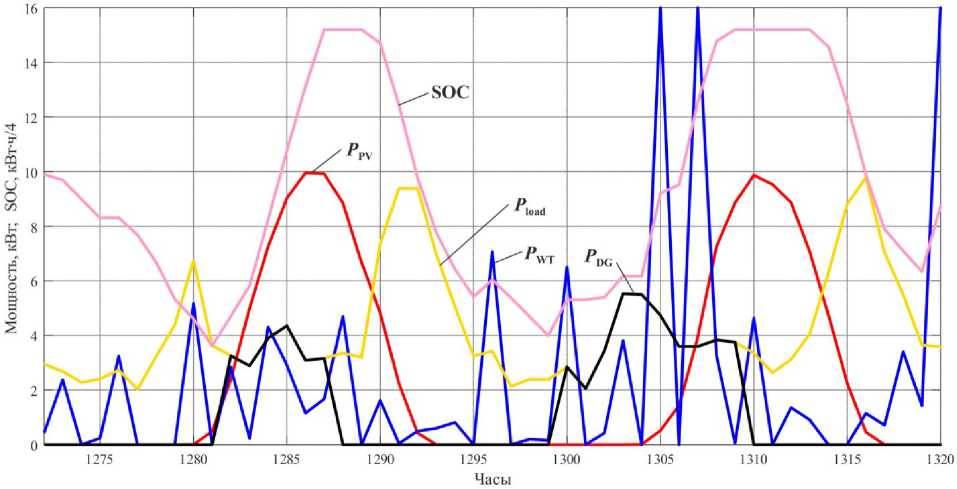
Рис. 5. Временные диаграммы режимов работы гибридной энергетической системы

состава оборудования HRES произвольной конфигурации, но и разработки эффективных алгоритмов контроля и управления режимами.

Результаты решения задач оптимизации состава оборудования HRES без DG представлены в табл. 3. Результаты получены для различных значений показателя вероятности потери питания LPSP*.

Полученные результаты свидетельствуют о том, что конфигурации HRES без гарантированного источника питания являются конкурентоспособными по величине LCC с конфигурациями HRES, представленными в табл. 2. Соответственно, данные конфигурации являются перспектив- ными для применения в энергетических системах, предназначенных для электроснабжения потребителей, не требующих высокого уровня надежности.

Заключение

Результаты проведенных исследований показывают, что предлагаемая методика может быть использована для выбора оптимального состава оборудования HRES различных конфигураций. Методика реализована в виде программного приложения в популярном математическом комплексе MATLAB, что обеспечивает удобство ее практического применения. В отличие от известных спе- циализированных прикладных программ, применяемых для оптимизации состава оборудования HRES [29], предложенная методика является гиб- кой и позволяет использовать для решения оптимизационной задачи различные критерии оптимизации и ограничения.