Оптимизация стратегий эксплуатации технических систем с проведением аварийных и профилактических восстановлений

Одной из возможностей обеспечения необходимых показателей надежности и эффективности работы технических систем является выбор оптимальной стратегии эксплуатации. В стратегиях эксплуатации будем рассматривать два типа восстановлений: аварийные, когда система восстанавливается после каждого случайного отказа, и профилактические, когда система восстанавливается в определенные моменты времени (не совпадающие с моментами отказов).

Рассмотрим две стратегии эксплуатации: стратегия C a - проводятся только аварийные восстановления, а стратегия C ₀ (стратегия строго периодических восстановлений) – в случае отказа системы проводится аварийное восстановление, если же система проработала без отказа заданный интервал времени т , то проводится профилактическое восстановление. В качестве критериев оптимальности стратегий будем рассматривать минимум интенсивности затрат на восстановления (средние затраты на восстановления в единицу времени) или максимум коэффициента готовности (вероятность того, что система работает в произвольно взятый момент времени).

Постановка задачи: обосновать выбор оптимальной по этим критериям стратегии из стратегий C_a и C ₀ , а также найти оптимальное время проведения профилактических восстановлений.

Пусть F_a ( t ) и F p ( t ) - функции распределений наработок до отказа после каждого аварийного и профилактического восстановления соответственно. В начальный момент времени наработка элемента до отказа имеет распределение F_a ( t ) . Время восстановления не учитывается. На рис. 1 представлен пример реализации такого процесса восстановления, где т , X 1 , X 1 +т , X 1 + 2 т , X ₂ , X 3 ... - моменты восстановлений системы, 5 1 , 5 ₂ , 5 3 ... — случайные времена между двумя последовательными аварийными восстановлениями.

Пусть R ( т ) - интенсивность затрат на восстановления, c a и c p - средние затраты на аварийное и профилактическое восстановление соответственно. Получим аналитическое представление R ( т ) .

Рис. 1. Процесс восстановления с профилактиками

Время функционирования системы разобьем на стохастически эквивалентные относительно длины и затрат циклы ( C i , ^ i ) , i = 1, 2, 3... , где c i - эксплуатационные затраты в i -м цикле, имеющем длину ^ i . Если ( C , ^_т ) - случайная пара с таким же распределением, как и пары ( c i , ^ i ) , то интенсивность затрат для рассматриваемой стратегии имеет вид [1]

R ( т ) =

E ( C ) E ( ^ т ),

где E ( X ) - математическое ожидание случайной величины X . Распределение случайной величины C приведено в таблице, где с - возможные значения величины C , p - соответствующие вероятности, F ( т ) = ¹ - ^F ( т ) .

Распределение случайной величины C

c	p
Ca	Fa ( т )
Ca + Cp	F a ( т ) F p ( т )
Ca + 2 Cp	Fa ( т ) F p ( т ) F p ( т )
Ca + 3 Cp	F a ( т ) ( F p ( т ) ) 2 F p ( т )
Ca + n Cp	Fa ( т ) ( F p ( т ) ) n 1 F p ( т )

Отсюда

E (C) = ЕCnPn = CaFa (т) + (Ca + Ср ) Fa (т) Fp (т) + n=1

• + (Ca + 2Ср ) Fa (т)Fp (т)Fp (т) + ■ ■ ■ + (Ca + nCp )Fa (т) (Fp (т))” 1 Fp (т) + '' =

= Ca Fa (т) + Fa (т)Fp (т) + Fa (т)Fp (т)Fp (т)+"' + Fa (т)(Fp (т))” 1 Fp (т) + - +

+CpFa (т)Fp (т)[1 + 2Fp (т) + 3 (Fp (т))2 +■ • • + n (Fp (т))” 1 + -

= C

X

Fa (т) + Fa (т)Fp (т)Е(Fp (т))

n - - 1

^{+ C}p F a ^{( т )} F p COZ n ( F p ^{( т )} ) =

• = Ca [ F (т)+F (т) f (т) / f (т)]+CpFa (т) Fp (2т) = CaFp (т)+. CpFa (т). a a         a p p2

( 1 - F p ( т ) )              F p ^{( т )}

XX

При выводе использованы формулы ^qn-1 = 1/(1 -q), ^nqn-1 = 1/(1 - q) при |q| < 1. Далее [2]: n=1

F ( t ) = P (^ < t ) = 1 - P (^ t ) = 1 - F a ( т ) fp ( т ) fp ( т- 2 т ) ,     2 т< t <  3 т ,

Mt) = P (^т < t) = 1 - Fa (т) (Fp (т))" 1 Fp (t - nт) ,

n т <  t <  ( n + 1 ) т ,

X_____           т             X   ____ n - 1 ( ^{n + 1} ) ^т

E (^t) = f F;т( t ) dt = f Fa ( t ) dt + E Fa (т)( Fp (т))”    J Fp ( t - nт) dt =

0                 0                ⁿ = 1                              n т

• т___         ___ т___       X ___

= J F (t) dt+Fa (т)J Fp (t) dt ^( Fp (т))n

0                         0             n = 1

т                            т

Fp (т)JFa (t) dt + Fa (т) JFp (t) dt

________0_______________________0___________

F p ( т )

Из (1) получаем выражение функции интенсивности затрат:

R (т) =         caFp (т) + cpFa (т)

V '    _ / X г т—_x , — _{z x} ст—, _x ,

FP MJ 0 Fa ( t ) dt + Fa MJ 0 Fa ( t ) dt

.

Если F a ( t ) = F p ( t ) = F ( t ) , формула (3) совпадает с известной формулой для интенсивности затрат стратегии строго периодических восстановлений [1; 3]:

r (,) = caF №cPFW J 0 F (t ) dt

.

Рассмотрим поведение функции R ( т ) при т^ 0 и т ^х . Так как F p ( 0 ) = 0, F a ( 0 ) = 1 и знаменатель дроби в (3) стремится к нулю при т ^ 0, то

где R1 (т) совпадает с функцией интенсивности затрат, если в ней c и c заменить на d и d соответст-ap                    ap венно. Из (6) следует, что максимум коэффициента готовности достигается в точке минимума функции R1(т).

Рассмотрим случай, когда наработки после аварийных и профилактических восстановлений распределены по экспоненциальным законам:

F a ( t ) = 1 - e - ^at , F p ( t ) = 1 - e - ^pt , a , p >  0.

В этом случае т____               1 т_____               1

J F a ( t ) dt =- F a ( ^т ) , J F p ( t ) dt = -F p ( ^т ) , 0 a 0 p

'

Fp (т) = pFp (т), Fa (т) = aFa (т), Fa (т) = -aF a (т),

lim R ( т ) = >» .

т^0 x 7

^{R ( т )} = apC a

F p ^{( т ) + C} F a ^{( т )}

Fp (т)(pFa (т) + aFa (т)) ,

X               X

Учитывая, что J F a ( t ) dt = ц a , J F p ( t ) dt = ц _p , где 00

цa и цp - средние наработки системы до отказа после аварийных и профилактических восстановлений соответственно, получаем limR (т) = са /Цa .                  (5)

т^х

^R '^{( т )} = apc a

__________Fa (т) У(т)__________ (Fp (т))2 (pFa (т) + aFa (т))2

где

У (т) =-capFp (т) + (a2 - ap)Fpp (т)-

с

Полученное значение Ra = — равно интенсивно-μa сти затрат стратегии Сa только аварийных восстановлений (профилактические восстановления не проводятся).

Рассмотрим стратегию восстановления C ₀ , в которой на аварийное восстановление требуется время d_a , а на профилактическое восстановление – d_p соответственно. Сопоставив каждому интервалу ^ i (случайное время между двумя последовательными аварийными восстановлениями) случайную величину y i -

^- cp 2 F p (^т) F a (^т)^- acpF p (^т) F a (^т) , ^c = c pl c a ^.

Заметим, что знак производной R ' ( т ) при т> 0 совпадает со знаком у ( т ) . Имеем lim у ( т ) =- acp <  0, т^ 0

lim у ( т ) = ( - cp + a - p ) a . т^х

Пусть выполнено неравенство - cp + a - p >  0,

или равносильное ему неравенство k <т^,                  (7)

1 + c где k = pl a . Тогда у (т) и вместе с ней R '(т) больше

суммарное время, потраченное за этот период на восстановления системы, получим так называемый альтернирующий процесс восстановления ( ^ i , y i ) . Распределения компонент этих пар совпадают с распределениями пары ( ^_т , Y а, где функция распреде

нуля, начиная с некоторого т ₀ >  0. Принимая во внимание равенство (5), заключаем, что прямая с уравнением R_a = с_а /ц _a является горизонтальной асимптотой графика функции и R ( т ) < с_а /ц a при т>т ₀ . Из (4) и вышесказанного следует, что существует значение τ* 0 <т * <т 0 , при котором функция R ( т ) принимает

ления случайной величины с_т приведена в (2), а рас

пределение случайной величины Y _т совпадает с распределением случайной величины C (см. таблицу), если в последнем c и c заменить на d и d соот- ap                     ap

наименьшее значение, причем R ( т * ) <  R_a .

Таким образом, при выполнении неравенства (7) для стратегии C ₀ имеется оптимальное время проведения профилактик, при котором интенсивность затрат меньше интенсивности затрат стратегии C_a

ветственно. Из формулы коэффициента готовности [1] для альтернирующего процесса восстановления имеем

K(tV___E (^т)___

⁽⁾ E ( Y _г ) + E ( ^ т ) ,

только аварийных восстановлений.

Из равенства (6) следует, что при выполнении не-

равенства

k < —, 1 + d

или

K (т) =

E ( Y J/ E (^) + 1 R 1 ( т ) + 1’

аналогичного неравенству (7), где d = d_p di_a при значе

нии т*, дающего минимум функции R 1 ( т ) , достигается

максимум функции K ( т ) - коэффициента готовности.

При F a ( t ) = F p ( t ) ( k = 1) R '(t ) < 0 на промежутке (0, co), функция R ( t ) монотонно убывает и R ( t ) >  R a . Следовательно, в этом случае профилактики проводить нецелесообразно, оптимальна стратегия только аварийных восстановлений.

Отметим, что на рис. 2 и 3 приведены графики функции R ( t ) при выполнении неравенства (7) ( k = 0,4, c = 0,3) и при его невыполнении ( k = 2, c = 0,3). В первом случае оптимальна стратегия с проведением профилактических восстановлений при т * = 0,489.

Кроме того, на рис. 4 и 5 приведены графики функции K ( t ) при выполнении неравенства (8) ( k = 0,2, d = 0,3, т * = 0,225) и при его невыполнении ( k = 2, d = 0,3).

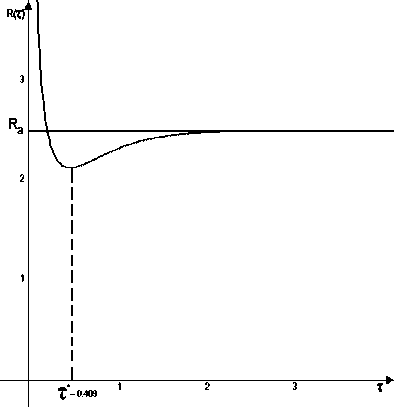
Рис. 2. График функции интенсивности затрат при k = 0,4, c = 0,3

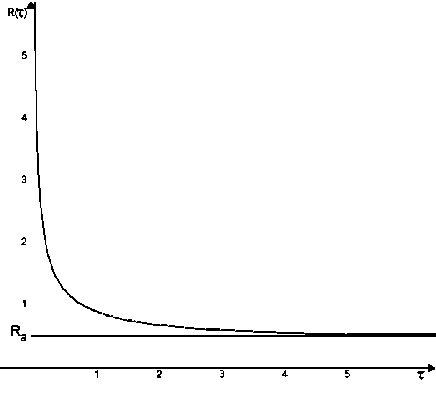
Рис. 3. График функции интенсивности затрат при k = 2, c = 0,3

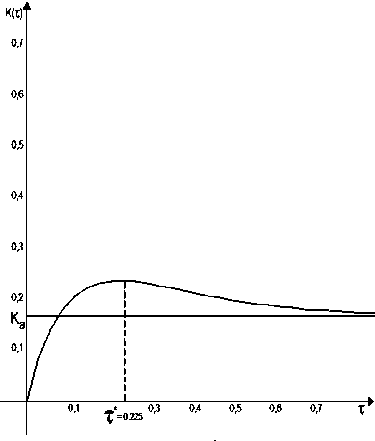
Рис. 4. График коэффициента готовности при k = 0,2, d = 0,3

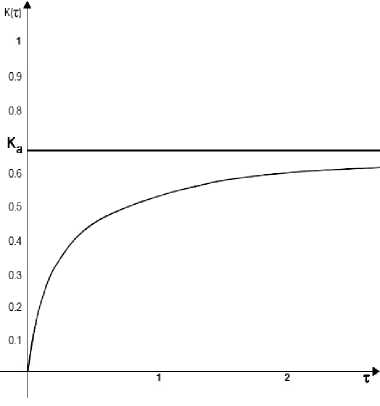
Рис. 5. График коэффициента готовности при k = 2, d = 0,3

Выводы, которые следует сделать на основании изложенного, следующие. В реальных условиях эксплуатации F a ( t ) * F p ( t ) , и потому для выбора оптимальной стратегии восстановления, наряду с другими стратегиями, следует рассматривать введенную в работе стратегию C ₀ . Полученное соотношение между стоимостями восстановлений и средними наработками до отказа (7) дает возможность выбора оптимальной стратегии из стратегий C ₀ и C_a .