Оптимизация структуры генерирующих мощностей децентрализованной энергосистемы с фотоэлектрической установкой

К зонам децентрализованного электроснабжения относится 70 % территории России, где, по разным оценкам, проживают от 10 до 20 млн человек. Высокая стоимость привозного топлива негативно влияет на технико-экономические показатели работы местных дизельных электростанций (ДЭС), однако полноценной замены им пока не существует. Одним из возможных вариантов экономии дизельного топлива может быть использование местных возобновляемых источников энергии (ВИЭ). Основным препятствием внедрения ВИЭ является недостаточное методическое обоснование проектов использования этих источников совместно с ДЭС [1, 2].

Аналитический обзор в области систем электроснабжения, включающих ВИЭ, позволил сделать вывод об отсутствии эффективных методов оптимизации комбинированной энергосистемы с учетом неопределенности связей между входными и выходными параметрами, реальных климатических условий места ее эксплуатации (солнечной радиации, скорости ветра, параметров водных ресурсов), особенностей графика нагрузки и режимных параметров ДЭС.

Авторами статьи предложен метод многоцелевой оптимизации структуры генерирующих мощностей энергосистемы, состоящей из дизель-генераторов (ДГ), фотоэлектрических модулей (ФЭМ) и аккумуляторных батарей (АБ).

При решении задач многоцелевой оптимизации критерий оптимальности оценивается целевой функцией

B ( x ) = ( f [ ( x ), f ₂ ( x ),... f_t ( x )), (1)

где f_i ( x ) ( i =1,2,…, k ) – заданные функции переменного x =( x ₁, x ₂,…, x_i ).

На переменные x i ( i = 1, n ) накладываются ограничения таким образом, что x принадлежит множеству Х его возможных значений. Необходимо найти точку x * ∈ X , обеспечивающую оптимальное значение функций f 1 ( x ), f 2 ( x ), …, f i ( x ).

Для решения задач многоцелевой оптимизации в системах энергетики наиболее распространенными оказались так называемые итеративные методы: метод наискорейшего спуска (для целочисленных переменных) и метод Бокса-Уилсона (при отсутствии явных аналитических выражений для целевой функции) [3].

Поэтому для начального этапа исследований оптимальных решений по какому-либо объекту энергетики с ВИЭ можно рекомендовать представление целевой функции с помощью аппроксимирующего полинома, коэффициенты которого оцениваются в результате опытов математического эксперимента, поставленных на модели объекта.

Пользуясь методами теории факторного эксперимента и математической статистики, можно определить значения коэффициентов полинома как коэффициентов регрессии и степень адекватности полиноминальной модели по результатам эксперимента.

Для решения задачи многоцелевой оптимизации предполагается использовать метод многофакторного эксперимента. В условиях проектирования эксперимент проводится не в натуральном виде, а средствами вычислительной техники.

Входные параметры варьируются по плану активного многофакторного эксперимента, а выходные параметры определяются экспертной оценкой.

Автономная энергосистема ДГ-ФЭМ-АБ представляется в виде аппроксимирующего полинома, поиск оптимума при этом производится на основе определения направления скорейшего подъема (максимального градиента) [4, 5].

В случае применения полиноминальной модели для оценки целевой функции B поиск оптимума осуществляется в два этапа: выход в район максимума B и нахождение полинома В = f ( x i - x 2 -—- x n ) вблизи оптимума.

На первом этапе решения задачи движение к оптимуму осуществляется с помощью линейной формы от точки с меньшим значением В к точкам с большим значением:

В = b 0 + b 1 x 1 + b 2 x₂ + ... + b n x n ,                                                (2)

где x – значения факторов; b – среднее значение показателя при среднем уровне всех факторов

i и bi – коэффициенты функции.

Коэффициенты b₀ , b₁ ,…, b_n определяются с помощью дробного факторного эксперимента в окрестностях некоторой начальной точки. Факторы варьируются в возможных пределах изменения их в данной задаче. Пределы варьирования устанавливаются экспертным п тем путем.

В качестве факторов, варьируемых в ходе оптимизации состава и мощности источников системы ДГ-ФЭМ-АБ, принимаются уровни мощности энергоисточников различного вида и накопителей электроэнергии. Например, для системы электроснабжения одного из населенных пунктов Республики Тыва с учетом величины нагрузки приняты следующие значения факторов:

x 1 – система ДГ с единичной мощностью 4 кВт;

x 2 – система ДГ с единичной мощностью 6 кВт;

x 3 – комплекс ФЭМ с мощностью панели 160 Вт;

x ₄ – комплекс ФЭМ, оснащенных трекерами, с мощностью панели 160 Вт;

x 5 – банк АБ с емкостью элемента 55 А∙ч;

x 6 – банк АБ с емкостью элемента 100 А∙ч.

Количество экспериментов, необходимое для определения коэффициентов b 0 , b i , связано с числом факторов [6]. Для получения математической модели процесса достаточно осуществить дробную реплику полного факторного эксперимента, положив x 1 x 2 = x 4 , x 1 x 3 = x 5 , x₂x₃ = x₆ , что значительно сокращает объем расчетов, так как уменьшает число вычислительных экспериментов до 8. План факторного эксперимента при выборе состава оборудования системы для шести факторов определяется дробной 1/8 репликой (табл. 1), в которой значения факторов «+1» отвечают верхним уровням, «–1» – нижним, а «0» соответствует среднему уровню.

По условию линейности зависимостей В ^ˆ и x максимум функции В ^ˆ будет иметь место при таком сочетании граничных значений параметров х , при котором все члены уравнения регрессии положительны, а незначимые равны нулю.

Применение факторного эксперимента дает возможность численно оценивать степень влияния каждого фактора на исследуемый выходной параметр В ^ˆ .

Таблица 1. План факторного эксперимента

Вариант энергосистемы	Факторы
	х 1	х 2	х 3	х 4	х 5	х 6
1	–1	–1	–1	+1	+1	+1
2	+1	–1	–1	–1	–1	+1
3	–1	+1	–1	–1	+1	–1
4	+1	+1	–1	+1	–1	–1
5	–1	–1	+1	+1	— –1	–1
6	+1	-1	+1	–1	+1	–1
7	–1	+1	+1	–1	–1	+1
8	+1	+1	+1	+1	+1	+1
Уровни факторов, кВт/кВт∙ч:
Верхний +1 Нижний –1	3х4=12 1х4=4	2х6=12 1х6=6	6,4 3,2	12,8 6,4	19,8 9,9	18 0

Если в результате первой серии экспериментов удалось определить состав оборудования, удовлетворяющий требованиям изолированной энергосистемы, дальнейшую оптимизацию можно не проводить.

В том случае, если В << 1 и состав оборудования не удовлетворяет требованиям системы, необходимо производить дальнейшее продвижение к оптимуму с уменьшением шага варьирования. Дальнейшее продвижение к оптимуму по методу Бокса-Уилсона производится с опыта варьирования, где средние уровни х равны полученным промежуточным оптимальным [5].

Для этого наиболее значимый фактор принимают за базовый x l и шаги варьирования остальных факторов принимают равными

^Х1Б = brr- ■ Л Б ,                                                         (3)

blλl где λiБ – новый шаг i-го фактора; λlБ – шаг базового фактора.

Шаг варьирования не может быть меньше единичной мощности генерирующего и аккумулирующего оборудования.

Движение от начальной точки осуществляется последовательными шагами λiБ , λlБ до тех А пор, пока оценки В по уравнению (2) не превысят в 1–2 раза максимально возможный уровень. После этого следует провести новый факторный эксперимент в области новой базовой точки с помощью нового дробного факторного эксперимента, выбрать новое направление движения и так далее до достижения оптимума [3]. Признаком оптимума по какому-либо фактору будет являться не значимость соответствующих коэффициентов полинома. Использование метода Бокса-Уилсона позволяет совершать движение к оптимуму по поверхности отклика с меньшим числом опытов за счет уменьшения шага варьирования.

С помощью описанной выше методики можно выполнить оптимизацию состава оборудования и мощности энергосистемы ДГ-ФЭМ-АБ для электроснабжения изолированных потребителей по алгоритму, представленному на рис. 1.

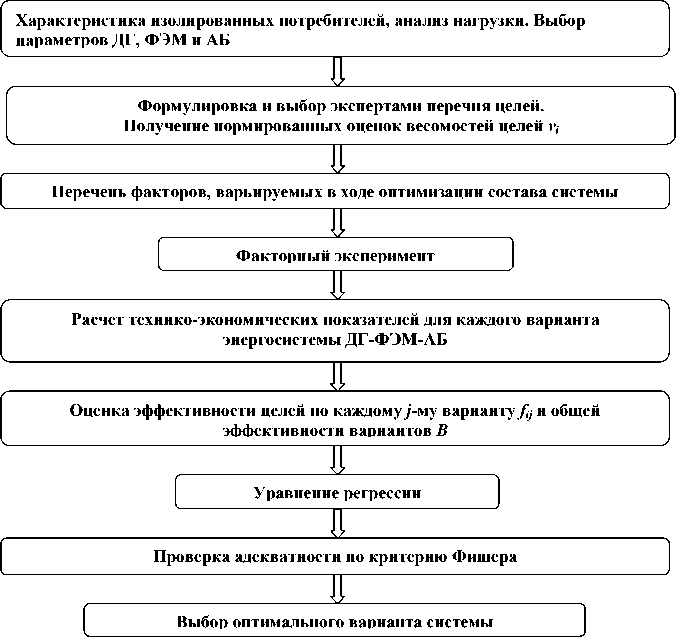
Рис. 1. Алгоритм оптимизации состава и мощности энергосистемы ДГ-ФЭМ-АБ для электроснабжения изолированных потребителей

Рассмотрим применение предложенного метода для оптимизации структуры децентрализованной системы электроснабжения населенного пункта Качык Республики Тыва.

Село Качык – одно из 12 населенных пунктов, получающих электроэнергию от ДЭС. Проведенные исследования показали, что место его расположения обладает значительным уровнем солнечной радиации [7].

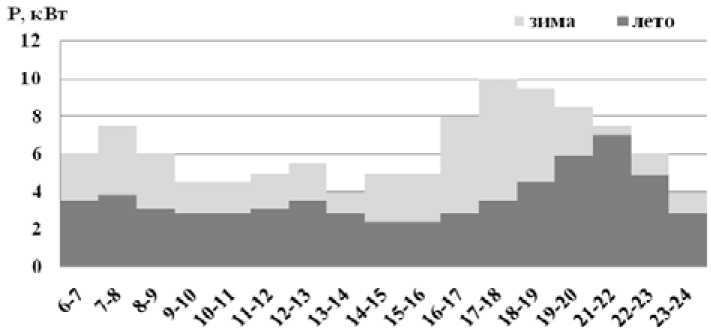
Электроэнергию жители получают от одного ДГ с установленной мощностью 30 кВт с 6 ч утра до 24 ч ночи, после чего ее отключают. По полученным данным были построены графики суточных нагрузок села в зимнее и летнее время (рис. 2). Максимальная потребляемая мощность 10 кВт приходится на 17 – 18 ч в зимнее время, минимальная 2,4 кВт – на 14–15 ч летом.

При выборе варианта исполнения и оптимизации состава агрегатов для автономной энергосистемы предлагается использовать обобщенный (комплексный) критерий эффективности B:

B = 1L vif i ( x ), (4)

где f_i ( x ) – значение переменной х по шкале i- го критерия; v_i – весовой коэффициент (весомость).

11родолжптслы1осп» времени, час

Рис. 2. Графики суточных нагрузок села Качык

Авторами статьи на основании анализа литературных данных, обобщения имеющегося опыта и опроса специалистов был определен предварительный перечень наиболее важных шести целей O i , требующих ранжирования (табл. 2). В группу экспертов вошли шесть компетентных в данной области специалистов: экономист-энергетик, специалисты по эксплуатации электростанций, специалист по фотоэлектрическим модулям, специалист-проектировщик электроустановок с ВИЭ . Число экспертов должно быть не меньше числа целей, учитываемых при сравнении вариантов системы ДГ-ФЭМ-АБ.

Для оценки весомостей целей использован метод ранговой корреляции [8]. При этом определялся коэффициент конкордации, показывающий степень согласованности мнений экспертов с ранжированием целей.

Каждой цели каждый эксперт присваивает оценочный ранг, определяющий, по мнению эксперта, весомость цели. Наиболее важная цель получает первый ранг ( а =1). Если какие-либо две или три цели невозможно различить по важности, то каждая из них получает ранг, равный среднему арифметическому присвоенных рангов. Обработка матрицы рангов [ a_ik ], где i – номер цели по перечню, k – номер эксперта, дает возможность оценки весомости каждой цели по формулам

A i = E ы a ik ; w i = ¹ " A i ( nN ) ^{- 1} + n ^{- 1,} v i = w i ( E n = 1 w i ) " ¹, (5) где N – число экспертов; n – число целей в перечне; A i – сумма рангов i -й цели.

Для оценки эффективности обеспечения целей в каждом варианте эксперимента был произведен расчет абсолютных значений показателей обеспечения целей по методике, описанной в [9]. Абсолютные оценки показателей обеспечения целей по вариантам приведены в табл. 3.

Для оценки эффективности обеспечения цели O ₄ в вариантах использовалась величина стоимости сэкономленного дизельного топлива в системе ДГ-ФЭМ-АБ. Показатели эффективности для цели O ₆ определялись по значениям чистой приведенной стоимости вариантов проекта системы.

Таблица 2. Перечень и оценки весомости целей в относительных единицах

Цели		Оценка весомости v i
O 1	Минимум капитальных затрат на строительство системы ДГ-ФЭМ-АБ	0,205
O 2	Минимум себестоимости электроэнергии, вырабатываемой системой ДГ-ФЭМ-АБ	0,051
O 3	Максимум удельной выработки электроэнергии ФЭМ на 1 кВт установленной мощности	0,308
O 4	Минимум расхода дизельного топлива на выработку 1 кВт∙ч электроэнергии ДГ	0,308
O 5	Минимальный срок окупаемости проекта ДГ-ФЭМ-АБ	0,103
O 6	Максимум привлекательности проекта ДГ-ФЭМ-АБ для инвестора	0,026

Таблица 3. Абсолютные оценки обеспечения целей по вариантам энергосистемы

Показатели	Варианты
	1	2	3	4	5	6	7	8
1. Кап.вложения в систему ДГ-ФЭМ-АБ, тыс. руб.	5537	3665	3683	5401	5401	4107	4170	6474
2. Себестоимость электроэнергии, производимой ДГ и ФЭМ, руб/кВт∙ч	15,38	25,02	25,05	15,18	11,18	21,68	21,78	12,78
3. Удельная выработка электроэнергии ФЭМ, кВт∙ч /1 кВт	270	154	154	270	307	191	191	307
4. Денежный эквивалент вытесненному дизтопливу, тыс. руб.	1561	1481	1481	1561	1481	1381	1381	1481
5. Срок окупаемости системы, лет	20,65	24,01	24,13	20,14	17,66	21,64	21,97	21,21
6. Чистая приведенная стоимость проекта, млн руб.	11,67	6,11	6,09	11,81	14,24	8,07	8,00	13,11

Нормированные относительные оценки эффективности обеспечения целей могут быть получены на основе линейного преобразования для прямой и инверсной зависимости этих оценок от абсолютной величины технико-экономического показателя по одной из формул f _  yt  ymin  .    f _  ymax  yi  .

ft =                  ;    ft =                  ;

ymax - ymin        ymax - ymin где ymax, ymin – верхнее и нижнее значения абсолютных величин технико-экономических показателей; yi – значение показателя для рассматриваемого варианта.

Результаты расчета относительных оценок обеспечения целей f_ij и общей эффективности B представлены в табл. 4.

В табл. 4 даны оценки эффективности вариантов: В – по комплексному критерию эффективности, В – по уравнению регрессии.

Условие ортогональности плана факторного эксперимента означает, что скалярные произведения для всех векторов столбцов матрицы планирования (табл. 1) равны нулю и все коэффициенты регрессии определяются независимо друг от друга, так как все ковариации cov { b_ib_j } равны нулю.

Таблица 4. Результаты расчета относительных оценок обеспечения целей и общей эффективности вариантов системы ДГ-ФЭМ-АБ

3 Ш s	Цели (коэффициенты весомости ) vi и оценки эффективности fij						Общая эффективность варианта
	1	2	3	4	5	6	V ifij i	В - b 0 + b 1 X 1 + ... + b n x n
	0,205	0,051	0,308	0,308	0,103	0,026
1	0,334	0,697	0,757	1	0,538	0,685	0,718	0,707
2	1	0,002	0	0,556	0,018	0,002	0,378	0,352
— 3	— 0,994	0	0	0,556	0	0	0,375	0,377
4	0,382	0,712	0,757	1	0,617	0,703	0,737	0,735
5	0,382	1	1	0,556	1	1	0,737	0,700
6	0,843	0,242	0,243	0	0,385	0,242	0,306	0,343
	0,82	0,236	0,243	0	0,333	0,234	0,295	0,265
8	0	0,885	1	0,556	0,452	0,862	0,593	0,623

Из условия нормирования следует, что все диагональные элементы ковариационной матрицы равны 1/ N и значения коэффициентов уравнения регрессии определяются по формулам, приведенным в [6]:

NN bo - V b 1 NV B                                        (7)

где N – число реализованных опытов k; B_k – значение выходного параметра, полученное на основе комплексного критерия эффективности с использованием экспертных оценок вышеуказанных компетентных специалистов.

Симметричные нормированные ортогональные планы дают минимальную дисперсию оценок по уравнению регрессии.

Коэффициенты проверяются на значимость по критерию Стьюдента. Коэффициент b j считается значимым, если выполняется условие

|bj\ > t s S ( b j ),                                                                                    (8)

где S ( b j ) – среднеквадратическая ошибка в оценке коэффициента b j ; t s – коэффициент Стьюдента с числом степеней свободы s = N – 1.

В нашем случае в уравнении все коэффициенты, кроме b 1 , являются значимыми, тогда уравнение регрессии примет вид

В = 0,517 - 0,017 x 2 - 0,035 x 3 + 0,179 x 4 - 0,02 x 5 - 0,021 x 6 .

Проверка адекватности полученного уравнения производится с помощью критерия Фишера по выражению

F ра^ч = SS ЧВ д "  F [ ( N - m - 1), ( m - 1)¹                                 (9)

где

N ₂

Ъ ( B k - В к )

S ²( B) ад =                   ,                                                            (10)

⁽ m + )

где Bk – значение выходного параметра, полученное из опыта на основе комплексного критерия А эффективности; В k – значение выходного параметра, полученного по уравнению регрессии.

В нашем случае 1,218 < 6,94, значит, условие (9) соблюдено.

По условию линейности зависимостей B и x при экспертных оценках максимум В будет иметь место при таком сочетании граничных значений параметров х , при котором все члены уравнения регрессии положительны, а незначимые равны нулю:

х 1 = 0, т. е. мощность ДГ равна 8 кВт;

х ₂= – 1, т. е. мощность ДГ равна 6 кВт;

х 3 = – 1, т. е. суммарная мощность установленных ФЭМ равна 3,2 кВт;

• х ₄= +1 , т. е. суммарная мощность установленных ФЭМ с трекером будет равна 12,8 кВт;

• х 5 = – 1, т. е. суммарная энергия, запасенная в банке АБ емкостью 55 А∙ч, равна 9,9 кВт∙ч; х ₆= – 1, т. е. суммарная энергия, запасенная в банке АБ емкостью 100 А∙ч, равна нулю.

Уравнение регрессии примет следующий вид:

В = 0,517 + 0,017 + 0,035 + 0,179 + 0,02 + 0,021 = 0,789 .

макс

Полученная структура системы ДГ-ФЭМ-АБ отвечает оптимальному решению. Генерирующая мощность изолированной энергосистемы для села Качык включает 14 кВт мощности ДГ и 16 кВт от панелей ФЭМ, кроме того, имеется 9,9 кВт∙ч электроэнергии, накопленной в АБ. Полученный вариант установленной мощности источников генерации, аккумулированной электроэнергии и состава энергосистемы полностью удовлетворяет требованиям для покрытия графика нагрузки потребителей.

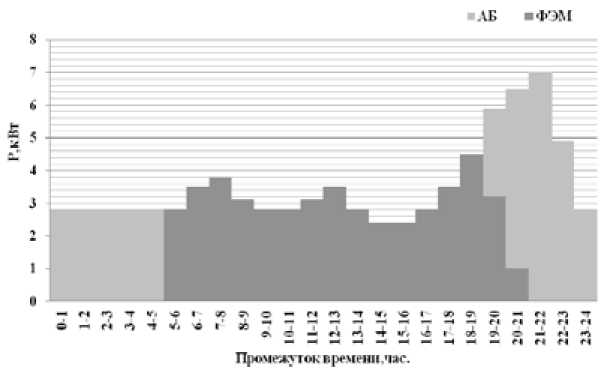
На рис. 3, 4 показано распределение генерирующих мощностей и использование энергии АБ в изолированной энергосистеме ДГ-ФЭМ-АБ для покрытия суточных летнего и зимнего графиков нагрузки.

Щюмеяят<жв|*ме«111,ч»с.

ЛБ -ФЭМ

Рис. 3. Распределение генерирующих мощностей в графике нагрузки летом

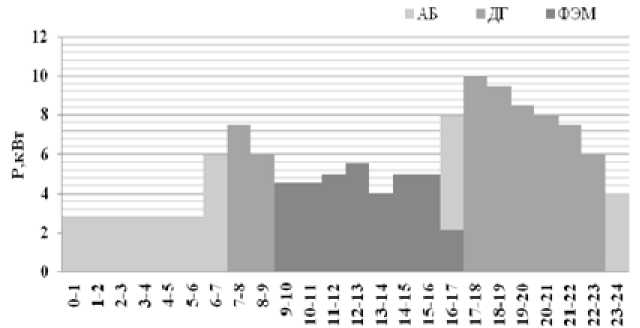
Промежуток вымени. час.

Рис. 4. Распределение генерирующих мощностей в графике нагрузки зимой

Результаты, достигаемые после создания энергосистемы ДГ-ФЭМ-АБ:

• •    график подачи электроэнергии изменен с 18 до 24 ч в сутки;

• •    будет снижено на 70 % потребление дизельного топлива по отношению к потреблению при 18-часовом графике подачи электроэнергии;

• •    уменьшено время работы ДГ с 18 до 3 – 5 ч в сутки в среднем в году, что позволит почти в 2 раза увеличить межсервисные интервалы для ДГ;

• •    улучшится качество электроэнергии;

• •    ФЭМ в составе системы будет вырабатывать от 55 до 100 % электроэнергии, потребляемой поселком в сутки.

Выводы

• 1.    Разработана методика оптимизации состава и мощности энергосистемы ДГ-ФЭМ-АБ для электроснабжения изолированных потребителей с учетом солнечного потенциала местности, технических характеристик дизельных и солнечных установок, аккумуляторных батарей и параметров нагрузки потребителей.

• 2.    Применение метода факторного эксперимента при оптимизации состава энергосистемы ДГ-ФЭМ-АБ позволяет учитывать в совокупности факторы, не зависящие друг от друга, а также показатели эффективности системы электроснабжения.

• 3.    На примере системы электроснабжения населенного пункта Республики Тыва определен оптимальный состав генерирующих и аккумулирующих установок с использованием фотоэлектрических модулей.