Оптимизация технологических процессов по системным критериям качества

Традиционные методы повышения технико-экономических показателей промышленных технологических процессов ориентированы на специфический характер производств, в которых они использовались в период доинформационных технологий. Так технологические процессы на предприятиях оборонного комплекса ориентированы на получение гарантированного качества безотносительно к затратам энергии, материалов и других ресурсов. Мелкосерийный характер производственных процессов, типичный для этих отраслей, обеспечивался созданием уникальных агрегатов под конкретные технологические операции, а немногочисленные разработки, связанные с их оптимизацией и адаптацией, имели ориентацию на повышение надежности и повторяемости промежуточных регламентированных технологическими инструкциями качественных технологических показателей: распределения температуры, концентрации упрочняющих элементов, толщины диффузионного слоя и т.п. в условиях неконтролируемых возмущений путем компенсации последних, либо удержания их на допустимом уровне. Это обстоятельство во многом определяет трудности модернизации оборонных производств, т.к. отсутствие гибкости технологических процессов требует капиталовложений на их перестройку зачастую превышающих стоимость создания новых производств.

В то же время в отраслях, ориентированных на гражданские потребности, отсутствие реальной конкуренции и жесткий распреде лительный характер потребления привели к созданию технологических процессов, ориентированных на массовое производство изделий, как правило, недостаточно высокого качества и высокой себестоимости. Работы по оптимизации процессов технологических процессов в этих отраслях были направлены на снижение затрат при сохранении и стабилизации усредненных, как правило, невысоких качественных показателей при массовом производстве.

Вступление в рыночные отношения при негарантированном сбыте, изменяющихся и повышенных требованиях потребителя для предприятий этих отраслей затруднительно. Выход на внешний рынок и внедрение международных стандартов качества (например, ИСО 9000), требующих "прозрачности" технологии для потребителя, вообще проблематичны без существенной переориентации целевых установок и технологической стратегии.

В качестве одной из мер для выхода из этой сложной ситуации автор предлагает создание гибких автоматизированных технологических модулей, позволяющих осуществлять комплексное оптимальное проектирование и управление технологическими процессами. Эффективность таких модулей в реальных производственных условиях обеспечивается системным подходом [1-4] к их созданию путем достаточно полного анализа жизненного цикла произведенных с помощью этих модулей изделий на основе декомпозиции глобального критерия оптимизации (интегративного системного свойства) технологических процессов.

Декомпозиция критерия

Разработанные в трудах [1-5 ] основные положения системного подхода позволяют наряду с получением оптимальных управляющих воздействий, регламентирующих соответствующие технологические режимы, определять оптимальные конструктивные параметры изделий и установок для их изготовления и обработки с позиций их дальнейшего оптимального функционирования при обеспечении предельных значений глобального критерия оптимальности как совокупного критерия, отражающего не только технико-экономические, технологические, но и эксплутационные показатели.

Для получения конструктивных результатов для технологических систем предлагается в качестве интегративного системного свойства глобальный критерий оптимальности, который определяется системным анализом жизненного цикла изделия и включает в себя в качестве взаимосвязанных элементов проектирование; технологию изготовления и обработки и эксплуатацию изделия.

Базисом предлагаемого в работе метода построения взаимосвязанных иерархических структур проблемно-ориентированных математических моделей и адекватных постановок комплексных задач оптимального проектирования и управления процессами технологической теплофизики является иерархическая структура локальных критериев оптимальности, полученная путем декомпозиции заданного глобального критерия.(см. рис.). На верхнем уровне иерархии рассматривается экономический критерий оценки жизненного цикла изделия - приведённый доход J_r J _r = 1 1д Х а л , ^т „к ( a ^в , ^т „ ^)- М а ^в , ^т „ ) 1 - j = 1

- K ^j^ „J " E c .      (1)

Здесь B j - годовой объем выпуска продукции j - вида при общем количестве N - видов продукции в номенклатуре, реализуемой по цене Ц _} ; 3 j - суммарные эксплутационные затраты на ее производство; K k - капитальные затраты при нормативном сроке их окупаемости E c ; a j , в j - обобщен

ные параметры, характеризующие эксплуатационные качества изделия и затраты ресурсов на его изготовление; T ^j- - продолжительность производственного цикла. Декомпозиция глобального критерия J _r производится на основании анализа входящих в формулу (1) компонентов, который выявляет её экстремальный характер из-за сложного нелинейного характера ее зависимости от параметров.

Условия роста прибыли, определяющие структуру декомпозиции глобального критерия Jr, формулируются в общем случае как условие его положительного градиента по

компонентам a , в , T ^j

d J _г да

> 0 ^;

d J_r    а

> 0.

дв     ’

dJ г

дт . „

^Т >0.

Удовлетворение условиям (2) является необходимым, но не исчерпывающим компонентом методики декомпозиции. Для достижения максимальной производительности технологической линии, участка из S установок при минимальных издержках, обеспечивающих максимальное значение критерия (1) необходимо в соответствии с системным свойствами целостности и структурируемо-сти рассматривать функциональный срез, включающий в качестве элементов оборудование соответствующей технологической цепи и позволяющий выделить в ней "узкие" места.

При соблюдении последнего из неравенств (2) максимум функционала (1) для технологической цепи в j -м производственном

цикле достигается при выполнении соотношения

^T „ 0 = minmax • + ^T _jTi;- ^T 0i + ^T ^j + ^T jT3 ) X e^ • •                                                                    ,

i = 1, s , где T0 j - оптимальная продолжительность j -го производственного цикла,

T jT 1 , T jT 2 , T jT з - фиксированное время подготовительно-вспомогательных работ,

0    ^0    0

t jj-\’^Tj,i , t jv+1 - минимально - возможная

продолжительность предыдущей, исследуемой и последующей технологической операций как результат решения соответствующих

задач оптимального быстродействия. Эти задачи ставятся как задачи с подвижным правым концом траектории в области конечных состояний Q ji е X ji ( Р, Т j,i ), определяемой, в том числе и допустимыми для последующей технологической операции начальными состояниями.

При этом область Qji = 3ji A Gj^+ является пересечением области 3 ji, достижимых состояний для данной i- ой технологи ческой операции и области Gj^+, допустимых по требованиям i+1-ой технологической операции состояний. Решение последовательности оптимальных задач на множестве

Q ji для каждого i-го элемента технологической цепи, позволяет определить оптимальные множества конечных состояний в областях достижимости, а также выявить технологическое оборудование, которым целесообразно управлять по оптимальному по быстродействию алгоритму. Для последующего и предыдущего оборудования, имеющего резервный ресурс времени формулируется задача оптимизации эксплутационных или ресурсных критериев при фиксированном времени.

Исследованы способы оценки погрешности отклонения результирующего состояния Xij(РТ0) от заданного X (Р) определяющие метрику, а, следовательно, тополо гию множества q ji, которые прямо следует из технологии, а следовательно определяет содержание математических моделей, отра жающих связи критериев качества техноло гии и эксплутационных критериев, полученных декомпозицией J г . В большинстве известных автору работ в качестве такой мет рики используется среднеквадратическое по объему v детали отклонение

) 1

^Р скв

^                       * \2         ^ 1

= j ta ^{p T ) -} x ф^{)) d v d T} —,

,                                              v '

V ^v

Б

где vБ - базовое значение объема, p е E - пространственная точка.

Такая метрика чрезвычайно удобна в вычислительной практике, а порождаемые ею через соответствующие условия трансверсальности решения оптимальных задач могут быть использованы при параметрической идентификации и адаптации.

Однако требования к оценке вектора состояний промышленной технологии существенно отличаются от р _скв , прежде всего, из-за возможных значительных локальных

*/ отклонений от X (Р) в узкой пространственной области, к которым нечувствительна эта оценка. Такие отклонения типичны для интенсивных видов нагрева, в частности индукционного, для химико-термической обработки с фазовыми переходами, в частности азотирования, и для ряда других ответственных технологических процессов. Кроме того, большинство технологических процессов регламентируется абсолютными величинами допустимых отклонений технологических параметров от заданных, например, лимитируется температурная погрешность при нагреве различных деталей, показатели прочности и надежности, отклонения глубины упрочненного слоя при ХТО и т.п. Поэтому в работе топология множества Q j i задается чебышевской нормой:

Р _ = max х _з (P T ⁰) - X (р) . pev ^{1 1}

Переходные режимы

В реальных процессах значительную часть производственного цикла занимают переходные режимы, связанные с запуском после перерыва, сменой темпа работы предыдущего и последующего оборудования, переходом от одной партии обрабатываемых изделий к другой и т.п. В установках для мелкосерийных производств, которые в рыночных экономических условиях занимают существенное место в производстве, доля этих переходных режимов зачастую не меньше, чем установившихся, а с учетом суммарных затрат на потери, связанных как с неустранимым браком, так и с исправлением устранимого брака (доцементация, передел и т.п.), а также с потерями производительности и простоями, оптимизация переходных режи- мов не менее существенна, чем установившихся. Наиболее остро эта проблема встает в случае использования в технологической цепи установок непрерывного или полунепрерывного действия. В этом случае вывод технологической цепи на стационарный режим может занимать несколько рабочих смен и требовать нетривиальных технических решений, например использования "балластных" заготовок.

Декомпозиция глобального критерия оптимальности J_r для переходных режимов приводит его к виду:

M 1      *

J _п = a £ к r = 1¹

- т ⁰ +

M1                                            M1

+ «2 Х|X r (Р,Т Пг )-X0 (P,T 0 ) + «3 £ Зэг , r=1

r = 1

*

где Tr, Тnr и Xг соответственно темп выдачи, конечный момент технологической операции и вектор состояний в переходном процессе, т0, X 0 (Р) - темп выдачи и результирующий вектор состояний в оптимальном стационарном режиме работы технологической цепочки; Ззг - соответствующая часть эксплуатационных затрат Зэ; в (1); M > M1 -общее число деталей в рассматриваемой партии, ai, a2, ag - весовые коэффициенты. Первое слагаемое учитывает суммарную потерю темпа выдачи изделий технологической цепочки в переходном режиме; второе -представляет собой соответствующую оценку отклонения вектора состояний Xr (p, Тnr ) в переходном режиме от его оптимального значения X0 (p, т 0 ) в стационарном режиме; а третье слагаемое характеризует часть эксплуатационных затрат на возмещение переходного режима. В качестве предельных частных вариантов возможно условие выдачи в переходном режиме всех M1 заготовок с удовлетворительными кондициями при допустимых экономических потерях за счет перевода второго и третьего слагаемых в состав ограничений a2 ~ ag ~ 0. При этом получаем задачу на минимум суммарной потери темпа в переходных режимах. Такая задача характерна для обработки ответственных дорогостоящих деталей. В случаях, когда изменение темпа работы оборудования невозможно или нецелесообразно а1 = 0 и а2 = 0 , задача сводится к оптимизации в переходных режимах отклонений выходных кондиций заготовок от оптимальных, что естественно приводит к некоторому их ухудшению на время переходного режима. Возможны и компромиссные решения при ai У 0 , a 2 ^ 0, ag ^ 0.

Математическое моделирование

Структурная декомпозиция глобального критерия оптимальности (1) порождает соответствующее "дерево целей" из совокупности локальных эксплуатационных и технологических критериев, которым соответствует "дерево моделей" (см. рис.). При этом соответствие моделей локальным критериям и определяет минимально допустимую сложность моделей. В соответствии с системным принципом иерархии и приоритетом целенаправленности математические модели в работе также построены на основе иерархического принципа на базе гомоморфизма моделей верхнего уровня по отношению к моделям нижнего уровня на основе агрегирования переменных состояния последних. Детализация описания возрастает по мере продвижения вниз по иерархическим ступеням на основе декомпозиции моделей верхнего уровня. При этом параллельно происходит декомпозиция глобального критерия (1). На каждой страте иерархической модели подсистемы формулируются в виде графа, в узлах которого размещены расчетные схемы - конструктивные математические модели - в агрегированных переменных. Такие графы отражают структуру подсистем и представляют собой структурные модели.

В постановке соответствующих задач оптимального управления и проектирования по локальным критериям оптимизации промышленных технологических процессов используются иерархические, структурные и

Системные модели

Управляющие факторы

Системы

Критерии

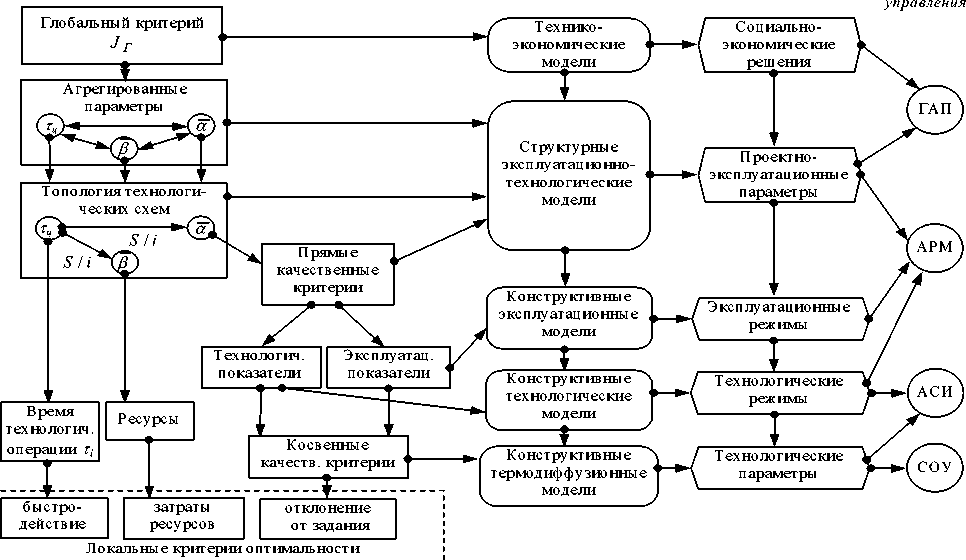
Рис. Взаимосвязанные иерархические структуры критериев, моделей и систем управления

конструктивные модели.

Следует отметить, что обычно удается выявить в группах моделей инвариантный базис. Так, например, конструктивные модели теплофизических процессов в большинстве промышленных технологий имеют общий термодинамический базис, что позволяет осуществить его вычленение с целью получения общих закономерностей оптимизации этих процессов.

Основу конструктивного математического описания таких технологических процессов промышленной теплофизики, как различные виды нагрева, термообработки, химикотермической обработки, пайки, фильтрации составляет неравновесная термодинамика, которая для основополагающих процессов тепло и массопереноса представлена как ква-зиравновесная в силу достаточно малой их интенсивности. Для обобщения математической формализации этих процессов использованы фундаментальные закономерности ква-зиравновесной термодинамики необратимых квазистатических процессов: линейный закон переноса и соотношения взаимности Онза-гера, согласно которым у -ый поток q у про порционален соответствующим термодинамическим силам U , у k

П qY = м LY kUY k , У = 1,2,3    (3)

с соответствующими кинетическими коэффициентами L y k .

В рассматриваемых типах термодиффузионных задач в твердых изотропных телах потоки носят смысл потока теплоты ( у = 1), массы ( у = 2), электромагнитного поля (у = 3 ) под действием обобщенных потенциальных сил, потенциалами которых является температура U^k (pT) = T(p,T) , концентрация U2k (p,T = C(p,T^ и напряженность магнитного поля U3k (p,T) = Ha (p, Т). При этом пренебрегаем недиагональными коэффициентами Ly k = 0, у Ф k увлечения, т.к. они при интенсивности рассматриваемых процессов незначительны (в 100 и более раз меньше эффекта прямого переноса). Тогда си- стема (3) распадается на автономные уравнения теплопроводности Фурье для температурного поля:

div( λ _a (T ,C )gradT) -

-

_ , dT _ , ’ c_a (T ) = F_1a (p, τ ) a _∂ τ 1a

дифференциального уравнения диффузии:

div(D _a (T ,C )gradC) -

A_j( χ ) ξ_τ ^(j) = B_{j - 0} ( χ )grad χ (p _{j - 0}) +

+ C _{j + 0} ( χ )grad χ (p_{j + 0} ) +

+ D j ( χ ) [ π ( χ , τ ,p j ) - π u ( τ ,p j )] ,

V p j е £ ^(j) XT ) Vt е (0, ~ )     ;    (8)

χ ( p j τ ) = χ 0 (p j ),

Vt = 0, V p j е Д . = int ^ . и £ ^{; (9)}

∂ C

-     = F_2a (p, τ )

∂τ и электромагнитного поля:

div( ρ _a (T )gradH_a ) -

( „ дн а ,      ’

- η k (H a ,T ) ^a = F 3a (p, τ ) k a       _∂ τ      3a

^гд^е П а = H a

^дЦ а ⁽ H а ) ∂ H_a

+ Ц а ( H a ), ^ а , Da

- коэффициенты теплопроводности и диффу зии, ра - удельное электрическое сопротив ление, са - теплоемкость, Ца - магнитная проницаемость. Конкретное определение краевых условий локальной удельной мощности источников (стоков) тепла Fya (p, Т) , вещества F^a (p, Т) или электромагнитного поля F3a (p, Т) в пространственной точке p е Д; Д = ^Д U S производится на основе материального и энергетического баланса в рассматриваемой пространственной области д , ограниченной поверхностью S .

В соответствии с этим, обобщенная конструктивная математическая модель термодиффузионных процессов формулируется в виде:

С t p,T ) - L j di^ J k j ( С )gra C (p . / t ) ] =

= W ( С ,P j , t ),

^Pj е int Ду c R , Vt е (0,~);(7)

где dx. . = ^, χτ =    ; ξτ =

∂τ∂

W ( x ,p, T ) = F_1a,F 2 _a,F_3a)^T ; t - время,

P j (l, z, y) - точка ограниченной в общем случае подвижными границами

J

Д' е д Д = Д, \intД, X ^д, = ^д

=1

области Ду трехмерного евклидова пространства с координатами l, z, У) ^ j = 1, J

- номер соответствующей фазы состояния обрабатываемого материала, J - общее количество фаз, отличающихся своими физико-химическими свойствами. В качестве компонентов вектора X в соответствии с вышеизложенным рассматриваются температура т, концентрация с и напряженность магнитного поля н , а матрицы коэффициентов kj(χ),Lj(χ),Aj(χ),Bj±0(χ),C j±0,D j(χ)

имеют соответствующую размерность. Индексом j ± 0 обозначены параметры состояния и коэффициенты в бесконечно малой окрестности границы ^ ^{( у )} j-ой области справа и слева от нее соответственно.

На основе системного метода построены взаимосвязанные иерархические структуры критериев оптимальности, проблемноориентированных математических моделей и адекватных постановок комплексных задач оптимального проектирования и управления достаточно широким классом процессов технологической теплофизики.