Оптимизация управления ресурсным обеспечением целенаправленного процесса командной деятельности в agile-ориентированных организационных системах

На современном этапе растет число организационных систем, в которых активные элементы (персонал) объединяются в команды для выполнения процесса целенаправленной деятельности [6]. С другой стороны, получает распространение адаптивный итеративный подход к реализации этого процесса, представляющий набор временных итераций, через которые он проходит от момента его инициализации управляющим центром до целедостижения. При этом управление итеративным процессом целедостижения строится с использованием Agile-методологий [9]. В дальнейшем организационные системы, использующие адаптивный подход, будем называть Agile-ориентированными. Этот класс организационных систем приобретает особую значимость в условиях цифровой трансформации [1] и цифрового управления [7].

Итеративный процесс целедостижения организуется на основе выполнения совокупности задач, распределенных между членами команды [3]. С целью реализации процесса управляющий центр выделяет на заданный временной период ресурсное обеспечение. В Agile-ориентированных организационных системах итеративный процесс строится в виде равных по длительности временных интервалов (спринтов). Расходование ресурсного обеспечения на реализацию одного спринта с учетом одинаковой длительности итераций и сохранением количества активных элементов на весь период целедостиже-ния, входящих в состав команды, характеризуется равномерным распределением между итерациями. Однако, расходы на реализацию стадий развития командной деятельности (формирование, конфликтная, нормирующаяся, исполнительная) [2; 10] неравномерные и определяются числом итераций, прогнозируемых для командной деятельности на каждой стадии.

Прогнозируемое ресурсное обеспечение используется для решений общего числа задач, определяющих целедостижения, которые, в свою очередь, распределяются между

Оптимизация управления ресурсным обеспечением целенаправленного процесса ...

членами команды. С другой стороны, в соответствии с последовательностью выполнения задач они распределяются между стадиями и итерациями. При подведении итогов спринта реальная степень выполнения задач в ряде случаев не соответствует прогнозируемой эффективности командной деятельности. В этом случае требуется перераспределение числа итераций на выполнение незавершенных задач, направленных на целедостижение. Часть ресурсного обеспечения, выделяемого на реализацию спринта, используется в качестве мотивационного для снижения числа незавершенных задач по сравнению с прогнозируемым распределением.

Каждые из перечисленных управленческих действий по распределению ресурсного обеспечения требует выбора варианта, обеспечивающего максимальную эффективность командной деятельности. С этой целью целесообразным является применение формализованного подхода, основанного на методах моделирования и оптимизации [4].

Целью работы является оптимизационное моделирование и алгоритмизация при управлении ресурсным обеспечением целенаправленного процесса командной деятельности.

Для достижения этой цели необходимо решить следующие задачи.

• 1.    Формирование оптимизационной модели и алгоритма принятия управленческого решения при прогнозном распределении и перераспределении ресурсного обеспечения между стадиями и итерациями.

• 2.    Оптимизация распределения мотивационного ресурсного обеспечения между членами команды по результатам выполнения задач.

Оптимизационное моделирование и алгоритмизация управления прогнозным распределением и перераспределением ресурсного обеспечения

Базовыми исходными данными для управления прогнозированием распределения ресурсного обеспечения являются следующие:

T – длительность процесса целедостижения командой Agile-ориентированной организационной системы в сроки, установленные управляющим центром;

• V    – интегральный объем ресурсного обеспечения, выделяемый для реализации целенаправленного процесса командной деятельности;

• m    = 1 , M - нумерационное множество задач командной деятельности, обеспечивающее достижение цели, заданной управляющим центром;

• n    = 1, N – нумерационное множество членов команды;

l = 1, L - нумерационное множество итераций процесса целедостижения.

Эффективность итерационного процесса командной деятельности характеризуется следующим процентным отношением, устанавливаемым в качестве задания управляющим центром для каждого спринта:

M

C = *- - 100%, l = 1, L ,                                     (1)

lM где Cl – эффективность командной деятельности на l-й итерации; Ml – количество задач, определенных управляющим центром как выполненных в полном объеме l-й итерации; M – общее число задач командной деятельности, обеспечивающее достижение цели.

Исходя из одинаковой длительности каждой итерации A T и установленной длительности процесса целедостижения определим общее число итераций:

T

L =---.

A T

Из условия равномерных распределений расходов ресурсное обеспечение, необходимое для реализации одной итерации, и = V. (3)

Тогда распределение ресурсных обеспечений между четырьмя стадиями целенаправленной командной деятельности пропорционально числу итераций, включенных в соответствующую стадию:

V = u L i , V 2 = u L 2 , V з = u L 3 , V 4 = u L 4 ,

где V ₁, V ₂, V ₃, V ₄ – объем ресурсного обеспечения, выделяемый для соответствующей стадии командной деятельности; L ₁, L ₂, L ₃, L ₄ – общее число итераций, соответствующее реализации каждой стадии.

При этом

V + V2 + V3 + V4 = V, следовательно, из (3) и (4) имеем

L 1 + L ₂ + L ₃ + L ₄ = L .                                 (5)

Формализацию и решение задачи оптимизации прогнозирования распределения ресурсного обеспечения между стадиями необходимо начать с прогноза оценок экспертов управляющего центра [5] желаемого изменения эффективности командной деятельности (1) с предположением, что все M задач выполняются на одной стадии за L итераций целедостижения в виде функций С 1 ( l ) , С ₂ ( l ) , С ₃ ( l ) , С ₄ ( l ) , приведенных на Рисунке.

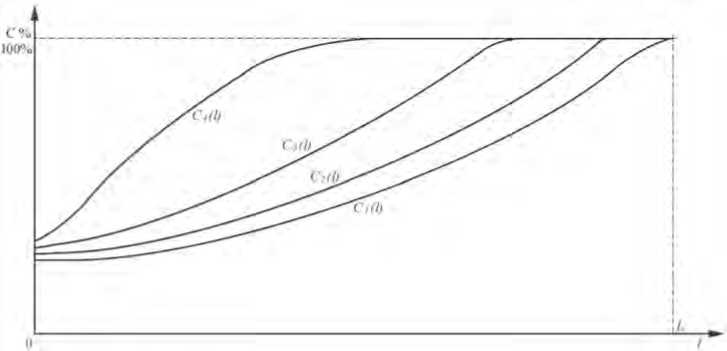
Функции изменения эффективности командной деятельности целедостижения, устанавливаемые на экспертном уровне

В формализованном виде задача оптимизации распределения ресурсного обеспечения с учетом (4), (5) по прогнозным функциям С 1 ( L 1 ) , С ₂ ( L ₂ ) , С ₃ ( L ₃ ) , С ₄ ( L ₄ ) представляется оптимизационной задачей, включающей экстремальное требование максимиза-

Оптимизация управления ресурсным обеспечением целенаправленного процесса ...

ции эффективности, граничное требование (5) и требования того, что значения оптимизируемых переменных L ₁, L ₂, L ₃, L ₄ выбираются на дискретном множестве 1, L :

max

^С 1 ⁽ L 1 ) + С 2 ⁽ L 2 ) + C 3 ⁽ L 3 ) + C 4 ⁽ L 4 ) ^              ,

L ₁, L ₂, L ₃, L ₄

L 1 + L 2 + L 3 + L 4 = L ,

L 1 = 1, L , L ₂ = 1, L , L 3 = 1, L , L 4 = 1, L

Для определения значений оптимизируемых переменных L ^*₁, L ^*₂, L ^*₃, L ^* ₄ применим алгоритм многошагового принятия оптимизационных решений [4]. Этот алгоритм требует предварительного введения параметров поиска:

Л2 = 1, L; 53 = 1, L; 54 = 1, L; 55 = 1, L, что позволяет перейти от задачи (6) к семейству следующих оптимизационных задач:

C 1 ( ⁵ 2 ) = max ^{[ С} 1 ( L 1 ) ]

1 < L < 5 2

^С 2 ⁽⁵ 3 ^jjmax ^{[ С} 2 ^{( L} 2 ^{) + С} 1 ⁵ 3 - ^L 2 У ]

^С 3 ^(з 4 ) = ^max ^ ^[ C 3 ⁽ L 3 ) ⁺ C 2 ⁽⁵ 4 - L 3 ) ]

C 4 ^{( 5} 5 ) = ^mOx. ^{[ С} 4 ⁽ L 4 ) ^{+ С} 3 ^{( 5 5} - L 4 У ]

где значения С 1 ( L 1 ) , С 1 ( 5 3 - L ₂ ) , С ₂ ( L ₂ ) , С ₂ ( 5 4 - L ₃ ) , С ₃ ( L ₃ ) , С ₃ ( 5 ₅ - L ₄ ) , С ₄ ( L ₄ ) определяются по экспертным графикам, приведенным на Рисунке.

На основании каждой из задач (7) при поиске максимума осуществляется полный перебор на множествах дискретных значений 1, L до окончательного получения оптимальных значений переменных L ^*₁, L ^*₂, L ^*₃, L ^* ₄ .

Эти оптимальные значения позволяют определить оптимальное распределение интегрального объема ресурсного обеспечения между стадиями командной деятельности:

********

V 1 = u L 1 , V 2 = u L ₂, V 3 = u L ₃, V ₄ = u L ₄.                        (8)

При равномерном распределении ресурсного обеспечения между итерациями управленческое решение (8) дает возможность осуществить прогнозное распределение общего количества задач командной деятельности, обеспечивающее достижение цели между стадиями:

****

LL LL

M, = M —, M ₂ = M —, M ₃ = M —, M ₄ = M— .           (9)

1 L 2 L 3 L 4 L

С учетом распределения (9) и значений функций эффективности для каждой итерации прогнозируется количество задач, которые определяются управляющим центром как выполненные:

**

M 1 1 = ^C 1 ( ¹ ) M i , ¹ = 1, L 1 ,

**

M 2 1 = ^C 2 ^{( 1} ) M 2 , ¹ = ¹ L 2 ,

**

M 3 1 = ^C 3 ^{( 1} ) M 3 , ¹ = ¹ L 3 ,

M 4 ₁ = C 4 ( 1 ) M 4 , 1 = 1, L 4 .

В том случае, когда результаты реализации итеративного процесса целедостижения на

1 -й итерации C(1) не совпадают с прогнозными значениями (10), требуется перераспределение ресурсного обеспечения по стадиям, которые охватывает нумерационное мно- жество итераций 1 +1, L .

Если 1 <  1 <  L ₁ , то эксперты формируют графики изменения C ₁ ( 1 ) , C 2 ( 1 ) , C 3 ( 1 ) , C 4 ( 1 ) , начиная со значения C '( 1 ) ; L ₁ <  1 <  L 2 - графики C 2 ( 1 ) , C 3 ( 1 ) , C 4 ( 1 ) ; L 2 <  1 <  L 3 - графики C 3 ( 1 ) , C 4 ( 1 ) ; L 3 <  1 <  L 4 - график C 4 ( 1 ) .

В соответствии с этими функциями изменения эффективности командной деятельности решается семейство оптимизационных задач с получением новых значений L ^*₁^', L ^*₂^', L ^*₃^', L ^* ₄ ^' и соответствующим пересчетом распределения ресурсного обеспечения (8) и количества выполняемых задач (9), (10).

Оптимизация распределения мотивационного ресурсного обеспечения между членами команды по результатам выполнения задач

Рассмотрим следующий механизм распределения мотивационного ресурсного обеспечения между членами команды: на первых трех стадиях командной деятельности осуществляется традиционное административное распределение; на исполнительной стадии, когда команда эффективно функционирует, для распределения используется формализованный оптимизационный подход.

В этом случае данные о результатах выполненных задач n - m ( n = 1, N ) членом команды и выделяемый n -му члену команды мотивационный ресурс на каждой 1 -й ( 1 = 1, L ₁ + L 2 + L 3 ) итерации спользуется для построения нейросетевой модели регрессии [8]:

d n1 = f ^(u n1 ) , ¹ = ^{1 L} 4 ,

где d _n1 - показатель степени выполнения задач n - m членом команды на 1 -й итерации; и_п1 - мотивационный ресурс, выделенный n -му члену команды на 1 -й итерации.

Предполагается определение значения показателя степени выполнения задач следующим образом:

d n1 = d 1 n1 + d 2 n1 + d 3 n1 + d 4 n1 ,                                (12)

где d1n1 =

A ₁ , если задача находится в исполнении , 0 , в противном случае ;

IА2, если задача готова d2 n1 = |                            0, в для проверки управляющим центром,

противном случае ;

Оптимизация управления ресурсным обеспечением целенаправленного процесса ...

d 3 nl =

A 3 , если задача находится на проверке, 0 , в противном случае ;

I A,, если задача определена как выполненная , d 4 nl = i 4

I             0 , в противном случае ;

Значения A ₁, A ₂, A ₃, A ₄ выбираются экспертом [5] в порядке возрастания на шкале [ 1, ^A ] ^.

Сформируем оптимизационную задачу, в которой переменными поиска управленческого решения являются объемы мотивационного ресурса, назначаемого n -му члену команды на l -й итерации достижения результатов командной деятельности, - u nl . При этом управляющий центр определяет интервал изменения мотивационного ресурса для конкретного члена команды.

minmax

Ц, < u«i < и« ,n = 1,N.

Экстремальное требование состоит в максимизации степени выполнения задач всеми членами команды на l -й итерации с учетом (12), (13):

NN

Tdnl =^f (Unl H max.

n=1

Граничное требование определяется интегральным объемом мотивационного ресур-

Vm l , выделяемого управляющим центром на l-й итерации командной деятельности:

N

T n <  v m , l = 1, L n .                              (15)

n = 1

Объединяя экстремальные требования (15) с граничными (14), (16), имеем следующую оптимизационную модель для l -й итерации:

N

T (Unl H max, n=1

N

1^ <  v m ,                           (16)

n = 1

min         max

^U n <  ^U nl <  ^U n , n = 1, ^N .

Для решения задачи (16) используется пошаговая схема рандомизированного поиска; считается, что величина u nl распределена равномерно на интервале (13). Тогда на первом шаге к = 1 устанавливается величина вариации переменной и_п1 max min —

4 i =  ------—, n = 1, ^ , l = 1, L 4 .                          (17)

На последующих шагах осуществляется коррекция значения u n на ( к + 1 ) -м шаге [5]:

» ^к + ¹ nl

)n + « ^{к + 1}

F (unl— ®nl)—F (ukl— ®nl) 2®kl где ак+1 - корректирующий коэффициент на (к +1) -м шаге;

а^{к + 1} = exp <  —Sigm

ГГп к,,^к ^+1 +Ц гЬ.^к к+ +Ц F ( ^Un/ ⁺ ®nl ) ^- F ( ^ton/ - ®nl )

к + 1

2®п1

F ( u k/ ¹ + to n/ ) ^- F ( u k ¹ + O n ) 2 ® ^к

а задается на первом шаге экспертом; to k ^{+ 1} - вариация интервала на ( к + 1 ) -м шаге.

Остановка пошагового поиска на k -м шаге осуществляется по правилу [4]

|u k - u „ V|< 5 , n = 1? N , / = 1, L 4,                          (18)

где 5 >  0 - величина, устанавливаемая экспертом на первом шаге.

В результате получаем оптимальное распределение мотивационного ресурса для каждой l -й итерации процесса командной деятельности на четвертой стадии развития команд:

u n/ = u k , n = 1, N , / = 1, L 4

Заключение

Оптимальное распределение ресурсного обеспечения является эффективным механизмом управления в Agile-ориентированных организационных системах.

Оптимизационный подход целесообразно сориентировать на четыре стадии развития командой деятельности. Стадии отличает учет возможностей команды в обеспечении це-ледостижения на основе прогнозирования экспертами управляющего центра количества задач, выполненных в полном объеме на каждой итерации (спринте). В этом случае распределение ресурсного обеспечения пропорционально оптимальному количеству итераций, включаемых в каждую стадию развития командной деятельности. По результатам реализации итерационного процесса осуществляется оптимальное перераспределение ресурсного обеспечения в том случае, если эти результаты не совпадают с прогнозными целями.

Для той части ресурсного обеспечения, которая направлена на мотивацию членов команды в итерационном процессе целедостижения, приемлимо использование оптимизационного подхода на четвертой стадии развития команды. Оптимальное распределение осуществляется с учетом данных о результатах деятельности каждого члена команды и использовании мотивационного ресурса на предыдущих стадиях.