Оптимизация выбора объема лечения доброкачественной гиперплазии предстательной железы с помощью нейронной сети

Введение. Большая часть мужчин после 50–60 лет начинает страдать от доброкачественной гиперплазии предстательной железы (ДГПЖ). Первые признаки ДГПЖ обнаруживаются у 8 % мужчин в возрасте от 31 до 40 лет. Затем частота этой патологии быстро нарастает и достигает у мужчин старше 61 года 70 % и больше. После 90 лет частота ДГПЖ может достигать 90 % [3, 5]. При профилактическом обследовании мужчин старше 50 лет ДГПЖ обнаруживается в 10–15 % случаев, однако клинические проявления болезни наблюдаются далеко не у всех. При этом у 80–85 % мужчин 60 лет и старше имеет место в той или иной степени увеличение предстательной железы. Усредняя множество имеющихся статистических данных, можно предположить, что клинические проявления ДГПЖ встречаются в среднем у мужчин 50–59 лет с частотой 15 %, 60–69 лет – 60 %, 70–79 лет – 70 %, 80 лет и старше – 80 %. Ретроспективный анализ показывает, что до 30 % мужчин сорокалетнего возраста, доживающих до 80 лет, оперируются по поводу ДГПЖ.

Многие пациенты отдают предпочтение медикаментозному лечению. Возникновение же грозных осложнений доброкачественной гиперплазии предстательной железы делает тактику консервативного лечения невозможной. Осложнениями ДГПЖ является острая задержка мо-чеспускания в результате отека увеличенной предстательной железы из-за нарушения диеты или передержания мочи, гематурия вследствие кровотечения из расширенных вен простатического отдела мочеиспускательного канала и шейки мочевого пузыря, острые и хронические воспалительные процессы в мочеполовых органах, хроническая почечная недостаточность, а также камни мочевого пузыря [5].

Современная диагностика ДГПЖ на первый взгляд несложна, но выбор оптимального метода лечения – чрезвычайно сложная, актуальная и дискутабельная проблема современной урологии. И в настоящее время поиск критериев прогноза исхода консервативного лечения ДГПЖ до начала лечения остается весьма важной и нерешенной проблемой, что и определяет ее актуальность [1, 6].

Целью исследования является улучшение результатов лечения больного с ДГПЖ путем оптимизации тактики с помощью нейронной сети, позволяющей спрогнозировать и предотвратить осложнения доброкачественной гиперплазии предстательной железы, путем своевременного изменения подхода к лечению.

Материалы и методы исследования. Для прогнозирования результатов консервативного лечения доброкачественной гиперплазии предстательной железы изучено влияние комплекса этиопатогенетических и клинических факторов. Исследование проводилось методом случай-контроль. Критериями включения в исследование явились пациенты с доброкачественной гиперплазией предстательной железы, пациенты с наличием осложнений доброкачественной гиперплазии предстательной железы, прооперированные пациенты. Исходным материалом исследования служили 849 пациентов, получавших консервативное (441) и оперативное лечение (408) по поводу доброкачественной гиперплазии предстательной железы в период с 2012 по 2015 годы.

В течение 4 лет и более осуществлялся мониторинг больных для выявления случаев прогрессии ДГПЖ, развития осложнений, хирургического лечения по поводу ДГПЖ. В зависимости от исхода заболевания пациенты поделены на контрольную группу – пациенты с благоприятным исходом, без признаков прогрессии ДГПЖ, осложнений (441 (53,20 %) человек) и опытную группу – больные с неблагоприятным исходом, у которых возникли осложнения ДГПЖ (182 (21,44 %) пациентов), прогрессия заболевания на фоне консервативной терапии

(142 (16,73 %) пациента) и 84 (9,90) пациента отказались от консервативной терапии, выбрав хирургическое лечение.

Для прогнозирования результатов консервативного лечения доброкачественной гиперплазии предстательной железы разработана нейронная сеть исхода результатов лечения в зависимости от этиопатогенетических, клинических факторов и подхода к лечению.

Условно исход заболевания поделен на благоприятный – пятилетняя консервативная терапия ДГПЖ без признаков прогрессии, сомнительно благоприятный – пятилетняя консервативная терапия с прогрессией ДГПЖ и/или появление относительных показаний к хирургическому лечению, неблагоприятный – консервативная терапия привела к хирургическому лечению, возникновению абсолютных показаний к хирургическому лечению. Соответственно исходу присвоено цифровое дискретное значение 1, 2, 3.

В качестве входного слоя нейронов использованы следующие параметры пациентов: возраст пациента, анамнез ДГПЖ, объем простаты по данным ТРУЗИ, скорость прироста объема простаты в год, уровень ПСА, уровень свободного ПСА, скорость прироста ПСА, наличие «средней доли», количество остаточной мочи, показатель урофлуометрии, данные IPSS, цифра IPSS обструктивные, цифра IPSS ирритативные, терапия альфа-адреноблокаторами в анамнезе, продолжительность терапии альфа-адреноблокаторами, терапия ингибиторами 5 альфа-редуктазы в анамнезе, продолжительность терапии ингибиторами 5 альфа-редуктазы, терапия М-холинолитиками в анамнезе, продолжительность терапии М-холинолитиками, применение малоинвазивных методов лечения ДГПЖ в анамнезе, употребление алкоголя, употребление острой пищи, фактор переохлаждения, фактор биопсии простаты, результат гистологического исследования биоптата, хирургическое лечение по поводу ДГПЖ в анамнезе, острая задержка мочеиспускания в анамнезе. Каждому признаку присвоено то или иное цифровое дискретное значение в зависимости от степени проявления признака.

Результаты исследования. Для моделирования прогноза исхода рака мочевого пузыря использовалась нейронная сеть. Обобщенная структура нейронной сети показана на рис. 1, где p – вектор входных наблюдений, в данном случае это результаты анализов в начале лечения. Один или несколько параметров входного вектора описывают используемый курс лечения. Размерность вектора p - R ; IW ¹¹ - матрица весов входного слоя; LW j - матрица весов от слоя j к слою i ; b ⁱ – вектор смещения i -го слоя; f ⁱ – функции активации i слоя; S ⁱ – количество функций активации в i -м слое; y – выходной вектор, в данном случае прогнозируемый результат лечения при заданных результатах анализов в начале лечения и используемом методе лечения, заданных во входном векторе p .

В нейронной сети каждый элемент вектора входа (для входного слоя это вектор p , для остальных вектор a ⁱ , где i –- номер предыдущего слоя) соединен со всеми входами нейрона и это соединение задается матрицей весов IW ¹¹ для входного слоя и матрицей LW j для остальных слоев. При этом каждый -й нейрон включает суммирующий элемент, который формирует скалярный выход n ( k ), к = 1 — S . Совокупность скалярных функций n ( к ) объединяется в S элементный вектор входа n функции активации -го слоя f . Выходы слоя нейронов формируют вектор столбец a , и, таким образом, описание слоя нейронов имеет вид:

n = f ( W*p + b ) .

Второй слой

Третий слой

Вход    Первый слой

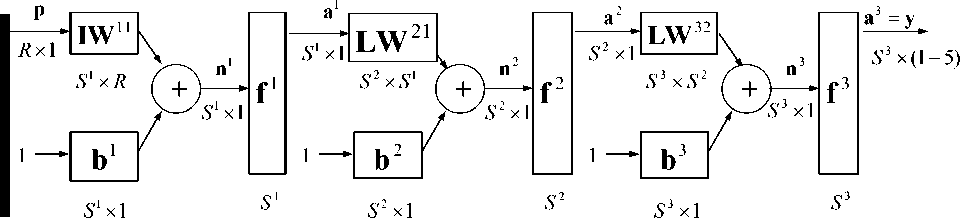
a ¹ = f ¹ ( lWⁿp + b ¹ )

a ² = f ² ( LW ²¹ a 1 + b ² )

a ³ = f ³ ( LW ³² a ² + b ³ )

Рис. 1. Структура нейронной сети

В качестве функции активации, в соответствии с рекомендациями из [6], используется антисимметричная сигмоидальная функция вида:

f ( x ) = —0,5 .

J X ! 1+ea

Программа, реализующая нейронную сеть, имеет следующие модули: модуль предварительной обработки и нормализации экспериментальных данных; модуль обучения нейронной сети; модуль диагностики.

С помощью модуля предварительной обработки производится выявление противоречащих друг другу экспериментальных данных, исключение повторяющихся выборок, нормализация исходных данных. Нормализация проводится в соответствии с рекомендациями, изложенными в [6], и заключается в приведении исходных данных к линейному участку функции активации, а именно к диапазону — 0,5 ^ 0,5. Подобная нормализация позволяет значительно повысить скорость сходимости алгоритма обучения нейронной сети.

Модуль обучения реализует алгоритм обратного распространения ошибки. В процессе обучения используется выборка из экспериментальных данных, включающих набор входов p и желаемых целевых выходов t . Во время этого процесса веса IW ¹¹ и смещения b настраиваются так, чтобы минимизировать некоторый функционал ошибки. Как правило, в качестве такого функционала для сетей с прямой передачей сигналов принимается среднеквадратичная ошибка между векторами выхода a и t [2, 4]:

J = 1 f f t q — «г ) 2 ,

² q = 1 i = 1

где J – функционал; Q – объем выборки; M – число слоев сети; q – номер выборки; S ^M

–

число нейронов выходного слоя; a q = « qM ] - вектор сигнала на выходе сети; t q = \t q ] - вектор желаемых (целевых) значений сигнала на выходе сети для выборки с номером q .

Рассмотрим выражение для градиента критерия качества по весовым коэффициентам для выходного слоя М:

дJ _ д д^МГ -KM

к

Q SM

1 SZ ( t q - a qM ) ²

² q = 1 к = 1                  7

Q SM

-хЯк q =1 к=1

—

aqM )

д a ^qM

где Q - объем выборки; S - число нейронов в слое; a q^M - к- й элемент вектора выхода слоя М для элемента выборки с номером q ; i - номер нейрона; j - номер входа.

Если S M равен 1 (количество нейронов в выходном слое равно 1), то дJ

д

Q

1 Я к

² q = 1

-

^a k ^qM

л

) ² l=- i ( t q

-

q = 1

Правило функционирования слоя М :

Г s m - ¹

akqM

= Jm Z к l=0

м «И^

_; q ^{( M -}D

, где к = 1, S M .

Если SM равен 1 (количество нейронов в выходном слое равно 1), то aqM

( _SM - 1

=fM z к l=0

« M a q ⁽ M ^{- 1)}

7

.

Следовательно, дaqM

0,

=⁴ f ' ( n^qM ) a^{q ( M - 1)}

к ф i

, к = i ,

• i о M • r\ mM -1

i = 1, S , j = 0, S .

Если SM равен 1 (количество нейронов в выходном слое равно 1), то д aqM

f '(n ^qM ) a ^{q ( M - 1)} .

После подстановки (1) в (2) имеем:

^Q k ( t q = 1

—

aq^M ) г_м(< W^{M - 1)}

•

Если SM равен 1 (количество нейронов в выходном слое равно 1), то дJ

5<

—

■ ]l ( t ^q - a* ) f M ( n q^M ) a q ^{( M - 1)} q = 1

.

Если обозначить

то получим

д J

К

Q

-Уа^(M-1), i = 1,SM,j = 0,SM-1. ij q=1

Аналогично выводятся соотношения для настройки весов «М ¹

слоя M - 1.

дJ

д® М — 1

Q SM

ХХ(

q = 1 к = 1

-

_nqM\_f, qMq_M\ д n ^qM  д a q ^{( M - 1)}

^ак  ) J M ^{(Пк  )}дa^{q (} M ^{- 1)} д«^{м - 1}

a^{q ( M - 1)} =

Q SM

-SZfc q=1 к=1

-

qM лqMSf qM4M\-nM дпк г qn4(M-1) Uq(M-2) - ак  )fM (Пк  )Шki g^q(M-1) fM-1 (ni      )aj      =

Q

- Я A q ( m - 1) a q ( m - ² ) q = 1

,

где

SM

Д' " -n ^

k = 1

—

ak" ) f"(< )°>ьЛ-, («Г ^-"

SM

)= Xд" f"^"-1>)

где i = 1, S ^{M - 1}.   (3)

vk=1     7

Для слоев М – 2, М – 3, … 1 вычисление частных производных критерия J по элементам матриц весовых коэффициентов выполняется аналогично. В итоге общая формула будет вы- глядеть следующим образом:

d J

Q

-^qaf ^{- 1)} q = 1

r = 1, M ,1, S^r , j = 0, S^{r - 1}.

где r – номер слоя

^ q

r + 1

XAf+1)

v k = 1

^

^ k*'

7

f k⁽ n k^r ) ,

r = 1, M - 1,

Дк " = ( t k - a k^M ) f " ( „ k" ) ) .

Для нейронной сети форма позволяет задать количество слоев, объем выборки Q и размер входного вектора наблюдений R , количество нейронов в каждом слое, выбрать тип функций активации для каждого слоя (сигмоид или линейная) и задать ее параметры. Для процесса обучения задается максимальное число циклов (эпох), точность аппроксимации как максимальная разница значений критерия для двух последних итераций, скорость обучения. Также указывается используется или нет в процессе обучения вектор смещения b ⁱ . В левой части формы в процессе обучения выводится значение критерия для каждой пятой итерации.

В процессе обучения использовалась генеральная совокупность 849 пациентов, прошедших лечение по поводу доброкачественной гиперплазии предстательной железы. Случайным образом из генеральной совокупности была сформирована обучающая выборка из 160 примеров. Оставшиеся 689 примеров вошли в проверочную (контрольную, тестовую) выборку. Количество нейронов во входном и промежуточном слоях было равно размерности входного вектора, R = S ¹ = S ² = 27 . Количество нейронов в выходном слое S ³ = 3, т.е. равно возможному числу исходов курса лечения. Поскольку для двухслойной сети после 90-й итерации наблюдается явление переобучения сети. При этом ошибка распознавания на тестовой выборке составила около 10 %. Для трехслойной сети явление переобучения не наступало до 800 итерации. При этом погрешность распознавания на тестовой последовательности составила менее 5 %.

Заключение. Таким образом, моделирование результатов консервативного лечения доброкачественной гиперплазии предстательной железы с помощью нейронной сети позволяет с высокой степенью достоверности предсказать конечный результат. При этом целесообразно применять трехслойную сеть с количеством нейронов в выходном слое, равном возможному числу исходов курса лечения. С помощью нейронной сети возможно выбрать оптимальную тактику лечения, меняя величину вектора входного слоя нейронов и оценивая величину вы- ходного вектора.