Оптимизация вычислительных процедур стохастических алгоритмов фильтрации и сглаживания, построенных на основе фильтра Калмана

К линейным динамическим системам (далее – ЛДС) относятся такие широко используемые в теории управления вероятностные модели, как скрытые модели Маркова (далее – СММ), динамические байесовские сети (далее – ДБС) и нейронные сети (далее – НС). На практике, как правило, возникают ЛДС с большим количеством оцениваемых параметров и состояний. В такой ситуации классические оценочные алгоритмы могут не давать требуемую точность вычислений. В связи с этим становится актуальной задача разработки модификаций классических оценочных алгоритмов, в частности фильтра Калма-на, направленных на повышение точности вычислений. В рамках работы предложены ал горитмы, оптимизирующие процедуры фильтрации и сгл аживания, построенные на ос © Полухин П.В., 2022

Полухин Павел Валерьевич кандидат технических наук, преподаватель кафедры математических методов исследования операций. Воронежский государственный университет, город Воронеж. Сфера научных интересов: машинное обучение; статистический и системный анализ данных; математическое и компьютерное моделирование; программные комплексы. Автор более 30 опубликованных научных работ.

нове фильтра Калмана. В качестве ЛДС рассматриваются скрытые марковские модели. СММ моделируют марковские процессы, определяемые начальным распределением вероятностей и вероятностным представлением переходов между состояниями в момент времени t и момент времени t + 1 . Для фильтра Калмана СММ в работе предложены численные алгоритмы, направленные на повышение точности вычислений. В рамках процесса моделирования формируются состояния X_{t +} к и X_{t +} к _{+ 1}, описывающие переменные двух смежных срезов, рассматривается случайный процесс с дискретным множеством состояний t = { t 1, t 2,..., t k } , процедура фильтрации СММ включает в себя одношаговое предсказание для момента t + к . В соответствии с алгоритмом дискретного фильтра Калмана переход для СММ из состояния X t и X t ₊ к выполняется с добавление шума, имеющего нормальную функцию распределения.

Математическая модель фильтра Калмана

Сначала кратко опишем семантику задания СММ. Они представляет собой вероятностную модель, предназначенную для моделирования стохастических процессов во времени и состоят из последовательности t = ( t , t + 1,.., t + к ) -состояний (срезов), каждое их которых характеризуется множествами наблюдаемых переменных X_{t +} к и свидетельств E 0: _{t +} к . Свидетельства поступают в виде непрерывного потока до текущего состояния t + к . Распределение вероятностей для свидетельств P ( E_{t +} к | X_{t +} к ) носит непрерывный (гауссов) характер с математическим ожиданием Е _{t +} к и ковариационной матрицей Q_{t +} к .

Для задания математической модели СММ необходимо определить следующие параметры: общее число состояний n , начальное распределение вероятностей P ( X_t ) для момента времени t = 0 , матрицу переходных вероятностей

T = ( T j ) = P ( X t + к = j | X t + к - 1 = i )

и матрицу восприятия

S = ( S ij ) = P ( E t + к = j | X t + к = i ) .

В рамках статьи будут в основном рассматриваться СММ, представленные в виде байесовской сети прямого распространения (см. Рисунок 1).

Оптимизация вычислительных процедур стохастических алгоритмов фильтрации ...

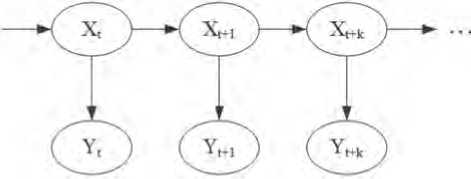
Рисунок 1. Пример фрагмента скрытой модели Маркова из k срезов

Введем матрицу переходов и восприятия в соответствии с введенными ранее обозначениями [3]:

T = ( T ij ) =

ft t 11

t 21

t 12

t 22

t t 1 n t 2 n

,

( t n 1

t n 2

t nn у

t ij = P ( X t + 1 = j | X t = i )

L -

f l ii

(0- ’" [ m

l 12

l 22

1 m

¹ 2 m

,

l j = P ( e t = j | X t

l m 1

= i У

mm у

Матрица переходных вероятностей T_k за k шагов получена из матрицы T в виде

T _k =T^k.

t k - P ( X t _{+ к} - j|X_t = i ) может быть

Полное совместное распределение по всем наблюдаемым переменным СММ, соответствующее состоянию t + к , будет иметь следующий вид при условии, что момент времени t принимается за нулевой [7]:

к-1

P(X0:к,E1:к ) = P(X0 )ПP(Xt+1| Xt )ПP(Et+1| Xt+1).

t-1

Сформулируем решение задач поиска распределения P ( X_{t +} к |E_{t +} к ) с использованием теории фильтрации Калмана. Для рассматриваемой модели будем использовать дискретный фильтр Калмана. Определим структуру фильтра Калмана:

^Xt + 1 = Д+1 ^Xt ⁺ w t ,

Е [ ^w _T

w

Q t , т - 1 , О, г ^ t ,

E t + 1 = H t + 1 ^Xt + 1 ⁺ v t + 1 ,

^Е [ v r

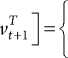
R t + i , t - 1 + 1, 0, t ^ t + 1,

где w t , v t + 1 - шумовые гауссовы процессы с соответствующими ковариационными матрицами Q t и R t + 1 ; F_{t + 1} - матрица перехода; H t + 1 - матрица измерений.

На основании введенных обозначений можно определить задачу фильтрации Калмана как задачу [5]

P ( X t + 1 I X t ) = N ( X t + 1 I F t + 1 X t , Q t ), P ⁽ E t + 1 I X t + 1 ) = ^{N (} E t + 1 I H t + 1 X t + 1 , R t + 1 )-

В соответствии с представлением (5) рассмотрим следующие выражения фильтрации:

P ( X t + 1 I E 1: t ) = N ( X t + 1 I X t + 1 , Ф t + 1 ),

P(Et+1 । E1:t ) = N(Et+1 । Ht+1 Xt + 1, St + 1), где Xt+1 - одношаговое предсказание Xt+1; Фt+1 = Д+1ФtFtT+1 + Qt+1 - ковариационная матрица, соответствующая переходу между состояниями Xt и Xt+1; Фt - скорректированная на предыдущем шаге ковариационная матрица вектора состояний; St+1 = Ht+1Фt+1HT+1 + Rt+1 - ковариационная матрица вектора ошибки.

Алгоритм фильтрации Калмана в общем случае включает в себе два этапа – предсказание и обновление. На первом этапе вычисляет предсказание для момента t + 1 в соответствии с матрицей перехода F_{t + 1} и текущим состоянием системы X t :

X о = Е [ X о ] ,

Ф о = Е[ ( X о -Е [ X о ] ) ( X о -Е [ X о ] T ) ] ,

X t + 1 = F t + 1 Xt ,                                                           (9)

Ф t + 1 = F + 1 E [ X _tX T ] F t + 1 + Е [ w n , w T ] =

= Ц+1Ф tFT + Qt, где Xо - оценка параметра Xо, соответствующая начальному моменту времени t = о . Рассчитывается ковариационная матрица ошибок измерений как

S t + 1 = H t + 1 Ф t + 1 H T + 1 + R t + 1 ,                           (10)

и определяется оптимальное значение коэффициента усиления G_{t + 1}, которое интерпретируется как степень доверия расчетной и эмпирической величинам. Выполняется процесса обновления значений параметров X_{t + 1}. С учетом введения коэффициента усиления Калмана G_{t + 1} и ошибки ковариации Ф _{t + 1}, вычисляемой в соответствии с выражением (1о), выражение (1о) с учетом введенного коэффициента усиления G_{t + 1} перепишем в виде [6]

^Xt + 1 = ^Xt ⁺ G t + 1 ^ t + 1 ,

где Y_{t + 1} - вектор отклонения фактического значения от расчетного; G t + 1 =Ф -+ 1 H t + 1 S t + 1 ^{- 1},

Ф t + 1 = ( I — G t + 1 H t + 1 ) Ф —+ 1 -

Оптимизация вычислительных процедур стохастических алгоритмов фильтрации ...

C учетом выражений (9), (10) и (11) можно определить априорное распределение по всем переменным запроса, соответствующим состоянию X t + 1 рассматриваемой модели [4]:

P ( X t , X t + 1 1^ 1: t ) = P ( X t + 1 X t ) P ( X t E b t ) =

= n ( X t + 1 FX , Q t ) N ( X t X t , R t ) ,

P ( X t + 1 , E t + 1 E t ) = N ( E t + 1 |X t + 1 ) N ( X t + 1 |E 1: t ) = = N ( E t + 1 | H t + 1 X t + 1 , R t + 1 ) N ( X k | X t + 1 R t + 1 ).

Рассмотрим сохраняющее в условиях ошибок вычислений положительную определен- ность квадратно-корневое представление ковариационных матриц Qt и Rt . Для этого необходимо определение квадратных корней At и At+1 для каждой их них. С учетом квадратно-корневого представления выражения (13) и (14) приведем к следующему виду:

P ( X t , X t + 1 |E 1: t ) = N ( X t + 1 |F t X t , A t ( A t ) T ) N ( X t X t , R t ) , ^{P ( X}t + 1 , ^Et + 1 ^{| E} 1: t ) = ^N f ^Et + 1 ^{| H}t + 1 ^Xt + 1 , ^At + 1 ( A t + 1 ) j ^X

X N ( Xk Xt+1 Rt+1), где Qt At (At) , Rt+1 At+1 (At+1) .

Выражения (13) и (14) задают в общем случае алгоритм классического фильтрации

Калмана и позволяют получить предсказание P ( X_{t +} k _{+ 1} |E 1 _{: t} ) для состояния t + к + 1 .

Сглаживание Рауча – Тюнга – Штрибеля

Для решения задачи сглаживания, направленной на получения распределения P ( X k |E _{1: t +} к ) , воспользуемся методом сглаживания Рауча - Тюнга - Штрибеля (далее -РТШ). Для этого сформулируем задачу сглаживания в терминах СММ [10]:

P ( X k E t + k ) = N ( X t | J X t , Ф t ) .                         (17)

Метод РТШ включает в себя на первом этапе стадию фильтрации Калмана для вычисления оценок параметров X ^ t . На втором этапе вычисляется X C S _{+ 1} на основе обратной фильтрации. Определим выражение для оценки X C t _{+ 1} в соответствии с выражением (5):

X i t + 1 = ^Е Ы1 X t + 1 - Д + 1 E t ,                            (18)

где E_t - свидетельства, поступившие на момент t + 1 ; F t + 11 - обратная матрица переходов между состояниями X_t и X_{t + 1}.

Для удобства дальнейшего вывода введем следующие обозначения для сглаженных характеристик (сглаженные значения параметров выделяются значком ^{s -} ):

0_t — Ф - 1 , 0 - — ( ф s ^-)^- zt =0 t X t , z - =0 ^- X t ^- .

Тогда, учитывая, что процессы wt, vt+1 являются шумовыми и между ними отсутствует корреляция, выражение для ковариационной матрицы Ф t+1, соответствующей оценкам

X_t , можно представить в следующем виде:

^Ф t + 1 =

( ф t ^-) ¹ + H T R ^{- 1} H

(ф/ )-1 + (ф t )-1

(^Ф ( ) - 1 + ⁰ -

- 1

где Ф { - матрица, полученная на стадии фильтрации.

Учитывая тождество Шермана – Моррисона – Вудбери (далее – ШМВ), перепишем выражение (20) в следующем виде:

f-Of    s-     f 1 f = t + 1 — t t " t + t t —

— ф / - Ф t 0 ^- ( I +Ф / 0 ^-) Ф t

По формуле (21) получаем значение матрицы Ф _{t + 1} при применении процедуры сглаживания. Равенство (21) позволяет сравнить элементы матрицы Ф { , полученные на стадии фильтрации, с элементами Ф _t на стадии сглаживания. Выражение (21) позволяет получить значения оценок всех предшествующих состояний X_t через соответствующие значения матриц ковариаций Ф { и Ф s ^- :

Г f V f s - V" S - I

X t = ^Ф t I (^Ф t ) X t ⁺ (^Ф t ) X t I ,

X t — X ^ t + ( Ф t Z - - G t X i { ) ,                                    (22)

Gt — Ф f 0 -(I+ Ф f 0 -)-1, где Gt – коэффициент сглаживания.

В процессе сглаживания РТШ решается задача обратной фильтрации, и рассчитываются значения ковариационных матриц Ф ^f и Ф s , соответствующих этапу фильтрации и сглаживания:

f s ^-1 — TT ^{f - s} I 1 77   —

{^Ф t ^+Ф t } = F t + 1 { ^Ф t + 1 ^+Ф t + 1 } F t + 1 =

I г                       - 11-1 1 ¹

— F t ^T + 1 W + ^- 1 +[ф -+ 11 - ( ф ^f - 1 ) J [ F t + 1

По аналогии с выражением (20), применив тождество ШМФ, упростим выражение (23) и получим следующее равенство:

Оптимизация вычислительных процедур стохастических алгоритмов фильтрации ...

{ф f +Ф Г} = FTt+1 (ф/- )-1 [ф f- -Ф t+1 ](ф/- )-1 Ft, t+1.

Учитывая выражения (21) и (22), получаем значение матрицы ковариаций Ф _t :

ф =ф f-®f T f- 1   f-           f- 1

фt = фt фt Ft+1 (фt+1) (фt+1 фt+1 )(фt+1) Ft+1фt .

Далее введем выражение для матрицы усиления A_t для момента времени t в виде следующего произведения:

At =фfFT [фf- ]-1 .(26)

С учетом матрицы усилений A_t получим обобщенное выражение для расчета ковариационной матрицы ф _t [9]:

фt = фf - Gt (фf- -фt+1) AT .(27)

Матрица ф _t непосредственно зависит от матриц ф ^f и ф { .

Обобщенное значение оценки X_t принимает вид

Xt = Xf + At (Xt+1 -Xtf+1).(28)

Из выражений (27) и (28) получаем полное описание процедуры сглаживания на основе метода РТШ; процедура носит рекурсивный характер. В связи с этим особое внимание стоит уделить определению начального отчета времени t = n . Исходное значение оценки -Xn и ковариационной матрицы фn, характеризующее начало этапа фильтрации, будет иметь следующее значение, полученное на этапе фильтрации Калмана:

-^         -^ г

X f n = ^X ^f > ^ф n = ^ф n , ,

где XC nf и ф { соответствуют состоянию t = n .

В процессе выполнения фильтрации возникает необходимость постоянного вычисле- ния ковариационных матриц шумов Qt и Rt и коэффициента усиления Gt+1. Оптимизация матричных расчетом позволит повысить эффективность процедуры фильтрации. Рассмотрим применение квадратно-корневых алгоритмов на основе разложения Холецкого, а также ортогонализации Грамма – Шмидта (далее – ОГШ). Алгоритм вычисления значе- ний матриц Q t и Rt на основе разложения Холецкого записывается в виде

Q i , к = Q i , k - L i , k L jk ,

L i , j = j , i = j ,

Li, j = Qk'j, i * j, Lj,j где значения i , j и k для нижнего и верхнего треугольного разложения принимают значения j = 1,2,..,n; i = 1,2,.., j; к = 1,2,^, j-1 и j = m,m-1,^,1; i = j, j-1,..,1; к = j +1,^,m соот- ветственно.

В матричном представлении разложение Холецкого можно переписать в виде верхнего (нижнего) разложения матрицы H :

__ — _ —т _____т

H = LDL T = UDU T .

В выражении (31) треугольной матрицей L или U будет являться матрица, содержащая единицы на главной диагонали. В соответствии с этим приведем выражение (30) к следующему виду:

Q i , k = Q i , k - U i , k D k , k U j , k ,

D j , j = Q i , j , ^Ujj = ^{1; i} = j ,

Q i , j

U j =       ^; i * ^j .

Выражение (32) является более эффективнымс точки зрения нахождения корней матриц H_{i , k} , так как исключает извлечение квадратных корней каждого из элементов матрицы для формирования положительно определенной матрицы L_{i , j} . Альтернативным подходом к оптимизации расчетов ковариационных матриц Q_t и R_t является использование ОГШ. Данный метод основывается на задании некоторого множества ортогональных векторов q = ( q 1 , q 2,..., q m ) с учетом того, что h ' = ( h 1 , h 2,..., h n ) будут линейно независимы:

qlq = q i ² = 1, i = j , q ^{e K} i , q T q j = 0, i * j

С учетом того, что h' можно получить через произведение параметров q j и b j , имеем

n h' = ^hjb,.                                     (34)

j = 1

Если матрица Q _t может быть представлена в виде совокупности ортогональных векторов q , запишем выражение ОГШ как

H = QL = [ q i , q 2 ,_

Г 1

l ₂₁

q n J :

. ^Zn i

0   .„ 0 ^

1    0   0

l n 2     l n 2    ¹ ,

где L - матрица, задающая переход между базисами q и h' .

С учетом того, что Q_t – ортогональная матрица, и для нее справедливо выражение (35), получаем

Q Q ^{( q} 1 , ^q 2 , ^ , ^qn )

q 1

2 q ₂

0 )

0    = diag { q i ² } •

2 q_n

Дополнительно к рассмотренным механизмам оптимизации могут быть использованы различные параллельные алгоритмы перемножения матриц.

Алгоритм Штрассена предполагает рекурсивное деление каждой из исходных матриц А и В размерностью n x n на 4 блока. В таком случае данный метод накладывает одно ограничение, связанное с тем, что n должно быть четным.

Оптимизация вычислительных процедур стохастических алгоритмов фильтрации ...

На Рисунке 2 приведем диаграмму Штрассена для умножения матриц A_ij и B_ij , имеющих размерность 2 х 2 . Данная диаграмма отражает последовательность проведения операций сложения и умножения для каждого из элементов рассматриваемых матриц [1; 2].

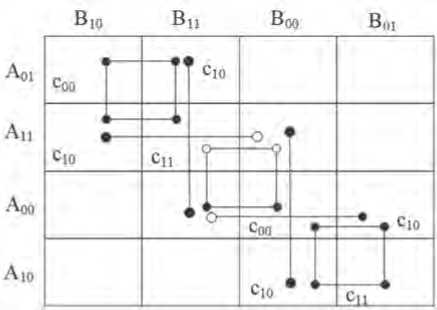
Рисунок 2. Диаграмма матричных операций Штрассена

Тогда вычисление произведения матриц A_ij и B_ij в соответствии с диаграммой Штрас-сена имеет следующий вид:

m 0 = A 00 B 00 , m 1 = A 01 B 10 , ^m 2 = ^{( —} A 00 + A 10 + A 11⁾⁽ B 00 ^— B 01 + B 11 ), ^m 3 = ( A 00 ^— A 10^{)( -} B 01 + B 11 ), m 4 = ⁽ A 10 + A 11^{)( —} B 00 + B 01 ), m 5 = ⁽ A 00 + A 01 - A 10 - A 11 ) B 11 , m 6 = A 11^{( —} B 00 + B 01 + B 10 - B 11 )-

Далее получаем

C 00 = m 0 + ^m 1 , c 01 = m 0 + m 2 + m 4 + m 5 , C 10 = m 0 + m 2 + m 3 + m 6 , C 11 = m 0 + m 2 + m 3 + m 4 -

Из выражений (38) и (40) получаем, что для вычисления матриц A_ij и B_ij необходимо выполнить 7 операций умножений и 18 операций сложения.

Вычислительный эксперимент

Численные методы оптимизации позволяют в достаточной степени повысить интенсивность процессов фильтрации и сглаживания на основе фильтра Калмана. Для моделирования СММ, а также решения вероятностных задач фильтрации и сглаживания на основе фильтра Калмана и алгоритма РТШ разработан набор программных компонентов, реализующих данные алгоритмы. В рамках решения задач численной оптимизации используется алгоритм матричного умножения по методу Штрассена, а также применение ортогонализации Грамма – Шмидта. В работе рассматриваются процессы фильтрации и сглаживания для СММ, однако предложенные алгоритмы можно достаточно легко адаптировать для решения задач вероятностного вывода любой их описанных ранее ЛДС.

На Рисунке 3 представлены численные характеристики фильтра Калмана и РТШ при шумовых коэффициентах к = 1 и к = 7 для распределений wt, vt+1.

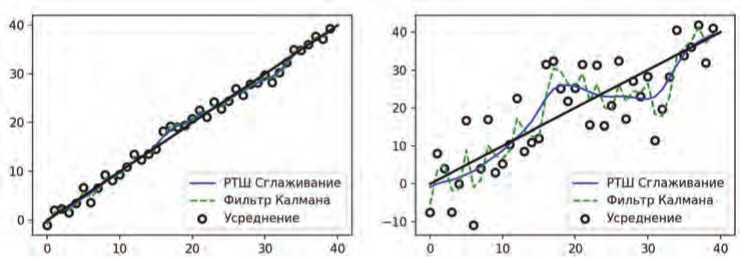
Рисунок 3. Сглаживание и фильтрация для модели СММ

Для оценки эффективности алгоритмов сглаживания на Рисунке 4 приведено сравнение РТШ с алгоритмом сглаживания с фиксированной задержкой (ФЗ).

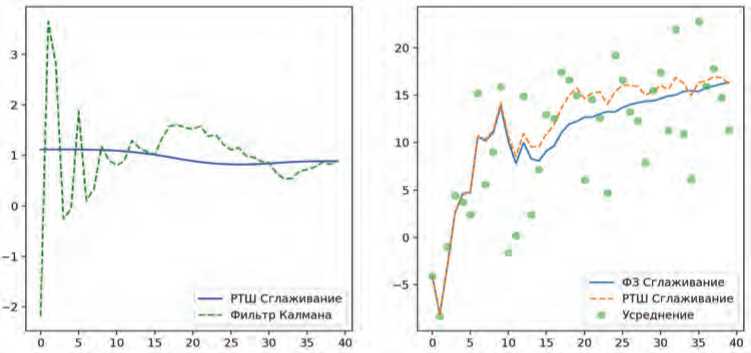
Рисунок 4. Сравнение алгоритмов РТШ и сглаживания с фиксированной задержкой (ФЗ).

Скорость сходимости РТШ и фильтра Калмана

Приведенные графики показывают, что РТШ достаточно эффективно сглаживает разброс выборок, полученных на этапе фильтрации. В свою очередь, сравнение ФЗ сглаживания и РТШ сначала демонстрирует идентичность получаемых генераций, однако с ростом числа выборок применение РТШ алгоритма становится более предпочтительным. В случае непрерывных распределений ФЗ лучше использовать совместно со сглаживанием РТШ, в противном случае на выходе можно получить распределение с достаточно большим значением дисперсии Е ( X I _t ) .

Оптимизация вычислительных процедур стохастических алгоритмов фильтрации ...

Заключение

Представленные в работе численные методы и алгоритмы оптимизации процедур вероятностного вывода в ЛДС, построенных на основе фильтра Калмана, показывают свою эффективность. Приведенные алгоритмы наиболее применимы для непрерывных распределений, а именно в том случае, если шумы w t , v_t + 1 представлены гауссовым распределением. Предложенные в работе расширенные алгоритмы фильтрации на основе LD , UD и ОГШ позволяют повысить устойчивость фильтра к возникновению нелинейных ошибок, позволяя для ковариационных матриц Ф { и Ф t - , соответствующих матрице F t _t + 1 , сохранять свойство симметричности и их положительной определенности на всем интервале принимаемых значений. Квадратно-корневой фильтр и фильтр на основе ОГШ позволяют исключить постоянную процедуру обновления Ф { и Ф s на основе решения уравнения Рикатти.

Другой важной особенностью разработанных алгоритмов оптимизации является возможность их использования в параллельных вычислительных системах, позволяющих в значительной степени повысить интенсивность решения задач вероятностного вывода. Такой подход достигается за счет использования параллельных алгоритмов Штрассена и поблочного разделения операций генерирования шумовых распределений w t , v _t + 1 .

Описанные алгоритмы могут быть использованы для решения широкого круга задач моделирования сложных стохастических процессов.