Оптимизация задачи управления запасами при случайном спросе

построенная на основе теории массового обслуживания, которая учитывает вероятностный характер спроса на запасы и при которой издержки на систему управления запасом, в том числе и потери, связанные с дефицитом запасов, минимальны.

Модель оптимизационной задачи управления запасами при случайном спросе. Анализ задачи управления запасами показал, что многие ситуации связанные с обеспечением запасами, можно рассматривать как задачи массового обслуживания [3, 4] – не только в том смысле, что потребители запасов могут простоять в очереди за ними, но и в том смысле, что запасы, ожидающие потребителей, также образуют очереди. Если потребители отсутствуют, то запасы увеличиваются. Если запасов в очереди нет, то имеет место дефицит запасов, потребители не обслуживаются. Если в качестве требований и заявок в системе массового обслуживания считать запасы, а обслуживающими устройствами – потребителей запасов, то зная интенсивность обращения потребителей, можно определить оптимальную интенсивность восполнения запасов, при которых издержки системы управления запасами минимальны.

Пусть спрос на запасы является пуассоновским с интенсивностью μ единиц в единицу времени, а длительность промежутка времени от момента подачи заказа до момента поступления партии запасов имеет показательное (экспоненциальное) распределение. При показательном законе и потоке событий с интенсивностью X среднее время доставки заказа составляет Т = 1/ X . Пусть при уменьшении уровня запасов до критического уровня Р заказывается количество запаса, равное Q единицам, таким образом, что

P + Q = M

,

где M – максимальный уровень запаса.

Будем считать, что максимальное количество запаса M известно. Тогда определению подлежит «точка заказа» P и объем партии Q . Очевидно, что определив любое из этих значений, второе можно найти из уравнения (1). Обозначим через P n вероятность того, что в наличии имеются n единиц запаса.

Применение правила «заказывать О единиц запаса, когда уровень запасов уменьшится до P , и заказывать M единиц запаса, когда уровень запасов уменьшается до нуля», означает, что:

• 1)    система массового обслуживания S переходит из состояния S n в состояние S n -1 при потреблении единицы запаса с интенсивностью ц ;

• 2)    система S переходит из состояния S n ( n ^0) в состояние S n+о и из состояния S o в состояние S m , при пополнении запаса с интенсивностью X.

Случайный процесс, протекающий, например, в системе S с шестью состояниями (максимальный запас равен пяти единицам, а точка заказа двум единицам запаса), показан на рис. 1.

f X Y A + X

^P2 ~ P 0 | ~ || -----

V A JV A

P3 = P0 IX

V A J

P 4 — P o\^X

V ^A J

P 5 — P o - V ^A.

где

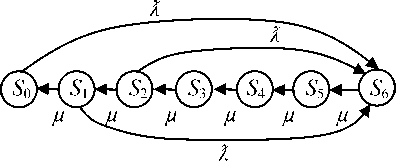
Рис. 1. Случайный процесс движения запасов при заказе партиями

На рис. 1 видно, что при отсутствии запаса делается заказ на пополнение запаса до максимального уровня. Далее, как только запас уменьшается до двух единиц, следует заказ запаса в количестве трех единиц. Пополнение запаса может наступить до прибытия заявки на запас (в этом случае система перейдет из состояния S г в состояние S 5 ), либо уже после очередной заявки и использования единицы запаса (в этом случае система перейдет из состояния S 1 в состояние S 4 ) и т.д. Например, для системы на рис. 1 получаем следующие уравнения для вероятностей состояний:

P — - 1p + + A P 1
dt ,	(2)
—1 — — X P 1 — A P 1 + A P 2 dt ,	(3)
—2 — — X P 2 — A P 2 + A P 3 dt ,	(4)
dP ^f -— A P 3 + A P 4 dt ,	(5)
dP 4 — XPx — A P 4 + A P 5 dt ,	(6)
—5 — X P 0 + X P 2 — A P 5 dt .	(7)

Стационарные решения системы уравнений (2) - (7) принимают вид:

P 1

,

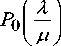
"■"I2 . A J ,

^A J

,

A + A- + X

„ 2

V     ^A      J

a!

P0

A + 5 A — + 6 a— + 3 X

В общем виде уравнения для вероятностей состояний системы с пополнением запасов партиями имеют следующий вид:

—°- - ^{- X} P 0 ^{+ A} P 1

dt                   ,            (14)

dP n dt

-X P n

- ^A P n ^{+ A} P n + 1

, для

n <  ^P , (15)

APn + !n + 1

dt                 , для ^P <  n - R , (16)

dP

,  — XPn - R — A + A+1

dt                         , для ^R <  n <  ^M , (17)

^M = A P + ^{X P} _M — r ^{— A} P M dt .

Стационарные решения системы уравнений (14) - (18):

z „ V „ \n — 1

p =p. fX )fA+X)

P n ¹ 0

^{V A JV A J} , для ⁰ <  ^{n - P} , (19)

P

P       I ^X |I A ^{+ X} I

Pn — P01             |

^{V A JV A J} , для P <  n <  M ^— P + 1 , (20)

где

P n

P I X ^P o I —

V A.

1 + ^{f A} ± ^- 1 P

V A J

—

, x n — Q — 1

A + X 1

A J

, для M — P + 1 <  n - M , (21)

( a + X ) ^P ( a + Q X )

Среднее число запасов, находящихся в системе в стационарном режиме определяется по формуле

n «

ЦP+1

Л --X

( ц + Л ) ^p ( ц + Q X ) ц

P

1 Г ^л ^J Г _p + 1 - p ^л ^J l ц J l ц J

I -l м (м +1) - p (p+1) Y ц + л J

.         ²         Jl Ц J

Следует обратить внимание на то, что формулы (22) и (23) для расчета вероятност и дефицита запасов P 0 и среднего числа запасов n являются приближенными. Это связано с тем, что не удалось на й ти компактные аналитические выражения для P 0 и n (далее будет показано, что нахождение оптимального решения задачи управления запасами даже при компактных приближенных выражениях приводит к сложным математическим выкладкам). Сравнение результатов расчетов P 0 и n , полученных по точным и приближенным выражениям, показало, что значения не сильно отличаются друг от друга. Максимальная относительная ошибка для разных M , P и Q не превышала 15%.

Обозначим через C 1 издержки выполнения заказа, а через C 2 – затраты на хранение единицы запаса. Если спрос на запас на горизонте управления составляет μ , то количество заказов в установившемся режиме будет равно μ / Q . Тогда общие издержки управления запасами, включая потери, связанные с дефицитом запасов составят

F = С 1 ц + С 2 n + С 3 P 0

^Q                ,       (24)

где C 3 – потери, вызванные отсутствием запасов.

Подставим в выражение (24) вместо P 0 и n выражения (22) и (23) соответственно, получим

F = С ^ц + С

¹ Q ³

( ц + Л )^P ( ц + Q X )

⁺ С 2

1 -Г мл

ц

ц ^{+ 1}

л

— X

( ц + Л ) ^P ( ц + Q X ) ц

X

P

I | P + 1 - P МЛ l          ц

+

Поскольку P и Q связаны уравнением (1) подставим в (25) M–P вместо Q:

+ С 2

F = С —У— +

¹ M - P ^{ц + 1}

Л

• —X

( ц + Л )^P ( ц + ( м - P) Л ) ц

P

1 -I ML I I p + 1 - p ^+A I l ц J l ^ J

Г ,      2

¹ -

[      ^ц _

₊ r M ( M + 1) - P ( P + 1) у ц + Л I ^P

+

ц

+ С 3

ц ^{p + 1}

( ц + Л ) ^P ( ц + ( M - P) X )

.

Возьмем производную от F по P и приравнивая ее к нулю, получим уравнение (27). Решая уравнение (27) можно найти оптимальное значение критического уровня запаса P, а по уравнению (1) оптимальный размер заказа Q .

Пример решения задачи оптимизации управления запасами. Рассмотрим пример использования предложенной модели для решения следующей задачи управления запасами. Пусть спрос на запасы составляет 200 единиц в неделю. Максимальный объем запаса на складе не должен превышать 60 единиц. Среднее время доставки заказа составляет 6,7 часов или 0,04 недели. Оформление одного заказа обходится в 500 рублей. Стоимость хранения единицы запаса в неделю обходится в 50 рублей. Потери от отсутствия запасов в течение недели составляют 10000 рублей. Требуется определить критический уровень запаса и размер заказа, при которых издержки будут минимальны.

Для начала из уравнения Т = 1/ Л . найдем интенсивность восполнения запаса Л :

Л = —

0,04

= 25

Далее, для найденного Л = 25 и заданных ц = 200, М=60, С1=500, С2=50, С32=1000 из уравнения (15) находим оптимальное значение критического уровня запаса Р*=6,949. Округляя решение до ближайшего целого получаем значение 7. Таким образом, «точка заказа» составляет 7 единицы запаса. Тогда оптимальная стратегия управления запасами будет заключаться в следующем: каждый раз, когда уровень запаса достигает 7 единиц, следует заказывать 53 единицы запаса. При данной стратегии вероятность дефицита Р0=0,042, средний уровень запаса n составит 31 единицу, а ожидаемые издержки будут составлять 3994 рублей.

C 1 ц        С ₃ ц ^{+ 1}ln( ц + Л )

( M - P )²   [ ц + Л ( M - P )]( ц + Л ) ^P

С ₃ ц^{р + 1} Л                С ₃ ц ^{р + 1} ln( ц )

[ ц + Л ( M - P )]²( ц + Л ) ^р  [ ц + Л ( M - P )]( ц + Л ) ^р

C 2 ц ^{P + 1} Л

P ц + Л | | ц + Л ц ) V ц

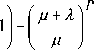
in f ^Л I f P - P ■     + 1

V ц К     ц

C ₂ ц ^{р + 1} Л ²

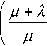
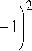
ц\ц + Л ( M - P )]( ц + Л ) ^P

P

( ц ^{+ Л} I Iр _Р ц ^{+ Л} ₊1 |  1

I-------I I P - P -------+ 1 I - 1   , _хр

V ц ) V       ц )   _f ц + Л | Г M ( M + 1) _ P ( P + 1) 1

f ц + Л           -V ц Л ^{2    -    2} J

I 1 I

I ц )

ц [ ц + Л ( M - P )]²( ц + Л ) ^P

C 2 ц ^{P + 1} Л

PP ц + ЛI f    11  f ц + ЛI  . f ц + Л |Г M (M +1)

|   I P +     I +1            I   lnI ц ) V   2)  ( ц )   I ц JL 2

P ( P + 1) 1

C ₂ ц ^{р + 1} Л ln( ц + Л )

C 2 ц ^{р + 1} Л ln( ц )

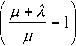
ц [ ц + Л ( M - P )]( ц + Л ) ^P

P f ц + Л I f р р+Л. +1 |  1

I-------I I P - P -------+ 1 I - 1   , _хр

V ц ) V       ц )   _f ц + Л | Г M ( M + 1) _ P ( P + 1) 1

f ц + Л             -V ц ) I ^{2     -    2} J

I 1 I

V ц )

ц [ ц + Л ( M - P )]( ц + Л ) ^P

P

I ц ^{+ Л} I I р р + ^{+ Л} +1 1   1

I------- I I P - P -------+ 1 I - 1   , _хр

V ц ) V        ц ) f ц + Л I Г M ( M + 1)   P ( P + 1) 1

f ц + Л               V) IJ

I 1 I

V ц )

ц [ ц + Л ( M - P )]( ц + Л ) ^P

= 0.