Optimization of Matched and Mismatched Filters in Short Range Pulse Radars using Genetic Algorithm

Published Online May 2016 in MECS DOI: 10.5815/ijigsp.2016.05.03

With increase applications of modern radar and ultrasonic systems, there is a constant need for increasingly better accuracy and increasing range resolution, with limited peak power. By using pulse compression technique in radar/sonar systems, these requirements can be met simultaneously.

The application of pulse compression coding in radars is to achieve the signal-to-noise ratio (SNR) benefits of a long pulse along with the range resolution of a short pulse [1, 2]. Pulse compression is a way to achieve the resolution of the short pulses while keeping within the practical constraints of peak power limitation. The process of modulating the transmitted pulse and then correlating the received signal with the transmitted pulse is known as pulse compression [3, 4].

Binary phase coding is one of the basic types of pulse compression, which encodes the transmitted pulse with information that is compressed (decoded) in the receiver of the radar.

The compressed pulse does not have appropriate sidelobes in range and that is the major disadvantage of compression; and for closely spaced targets, the resolution range is limited. A major problem of pulse compression techniques is weak sidelobes suppression. One of the best techniques for sidelobes suppression is using a mismatched filter in the receiver.

Matched and mismatched filter has an important role in pulse compression technique; therefore, its properties and characteristics are explained briefly. The most unique property of the matched filter is that it produces the maximum achievable instantaneous SNR at its output when a signal plus additive white noise is present at the input [5].

There are three ways to optimize the efficiency of the radar system [6]:

• •    Optimization of the receiver filter (matched or mismatched filter)

• •    Optimization of the transmitted signal

• •    Joint optimization of them

In this paper, we have decided to use the third method.

To do this, we first optimize transmission Codes with an innovative approach. The results are given in table (2). Then, using the floating point genetic algorithm that is shown in table (1), we optimize the received filter coefficients.

The rest of the paper is organized as follows: In Section II, the basic concepts involved in the matched filter and auto-correlation function are introduced. In section III, genetic algorithms are introduced. In section IV, problem formulation is derived. Section V presents simulation results. Finally, in Section VI the conclusions of this paper are presented.

• II.    Review of Fundamental Concepts

First, some basic concepts must be introduced. In this section, the basic concepts including theoretical foundations of matched and mismatched filter and autocorrelation function are explained.

• A.    Matched Filter Theory

Matched filter is obtained by correlating an unknown signal with a known signal or template to detect the presence of the template in the unknown signal. This is equivalent to convolve the complex conjugated time-reversed version of the template with an unknown signal. The matched filter is the optimal linear filter to maximize the signal to noise ratio (SNR) in the presence of additive stochastic noise. Matched filters are commonly used in radar, in which a known signal is sent out, and the reflected signal is examined for common elements of the outgoing signal.

The basic concept of matched filters evolved from the effort to obtain a better theoretical understanding of the factors leading to optimum performance of our system.

The characteristics of matched filters can be designated by either a time response function or a frequency response function, each being related to the other by a Fourier transform operation. In the frequency domain, the matched filter transfer function, H(f), is the complex conjugate function of the spectrum of the signal that is to be processed in the optimum method. Thus, the transfer function of a matched filter has the form [7, 8]:

H (f ) = KS * (f) e - j (1)

Energy of a sequence and Signal to noise ratio is given by (5)

N - 1

E = 2 ^ Y ² ( n )             (5)

n = 1

SNR =--- (6)

E_{N 0}

w here E denoted as input noise power.

The peak sidelobe level (PSL) and the integrated sidelobe level (ISL) are two important parameters for radar performance analysis. A measure of the largest sidelobe as compared with the peak of the compression is known as PSL and a measure of the total power in the sidelobes as compared with the peak of the compression is ISL [9]. For an N bit code:

P^SL = maX n ^ ₀ (| Y ( n )| )            (7)

ISL = 10 /og₁₀

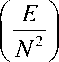
Another parameter that has been a subject of considerable interest is the merit factor (MF), which is closely related to ISL [10].

Where S(f) is the spectrum of the transmitted signal S(t), K is a constant for normalization, and T is a delay constant required to make the filter physically realizable.

The output of the matched filter is obtained as (2):

MF = — E

y ( t ) = J a ( t ) s ( t - T ) dT              ⁽²⁾

Where:

y(t) = Auto-correlation.

h(t) = Compression filter coefficients.

s(t) = Transmitted pulse compression code.

T = Correlation delay.

• B.    Auto-correlation function

The auto-correlation function (ACF) of a discrete coded waveform can be given as (3):

N - 1

Y ( n ) = Y a ^a + n             (3)

n = 0

Main Lobe (ML) is defined as the absolute maximum value of ACF (4).

ML = max ( Y ( n ) )

Good sequences are associated with small PSLs and large MFs.

• III.    Floating point Genetic Algorithms

GA [11], are heuristic procedures that are often able to locate near optimal solutions complicated problems. To do this, a GA keeps a set of trial solutions, and forces them to evolve towards an acceptable solution. First, a representation for possible solutions must be developed. Then, starting with an initial random population and employing survival-of-the-fittest and exploiting old knowledge in the gene pool, each generation's ability to solve the problem should improve. This is achieved through a four-step process involving evaluation, reproduction, recombination, and mutation [12, 13].

• A. Heuristic Crossover

Crossover in GA is a genetic operator that used to vary the coding of a chromosome or chromosomes from one generation to another one. It is similar to the reproduction and biological crossover, upon which GAs are based. A crossover is a process of producing a child solution from more than one parent solution [14].

A linear extrapolation of the two individuals is produced. The direction of the search is determined by using values of the fitness function. It produces two children I ^{A ( new )} and I ^{B ( new )} from two parents I ^A and I ^B . According to the following provided I ^A is better than I ^B in terms of fitness [15-17]:

This is the unique operator responsible for the fine tuning capabilities of the system, so that it can escape from local minima. It randomly changes one variable of a parent. It is defined as follows: for a parent I ^A , if the variable I ^A was selected at random for this mutation, the

• k , result is:

  P A ( new ) = I^A + r ( I A - I B )

  
  

  i" = ( i? i kA , - , i k )          (13)

  
  

  B ( new )      A

  
  
  
  

  Where (r) is a random number between 0 and 1.

  
  

  Feasibility = 1, if a <  I/ A ' new ) <  b = 0, otherwise

  
  

  Where a and b are lower and upper bounds of each variable in population. If feasibility is equal to zero, then another random value (r) is generated and another solution produced. If after (t) attempts no new solution meeting the constraints is found, the operator gives up and produces no children, i.e., the children become equal to parents and stop [15-17].

  B. Mutation

  Mutation is a genetic operator used to maintain genetic diversity from one generation of a population of GA chromosomes to the next. It is similar to biological mutation. Mutation varies one or more gene values in a chromosome from its initial state. In mutation, the solution may change entirely from the previous one. Hence, by using mutation, GA can come to better solutions. Mutation occurs during evolution according to a low mutation probability. If it is set too high, the search will turn into a primitive random search. This probability is user-definable [14].

  
  

  IV. Problem Formulation

  Now, the problem can be written in mathematical format.

  It is desired to find an N-bit binary sequences for matched filter whose PSLs or ISLs have the minimum value among all 2N existing codes and find M-bit (M>N) sequences for mismatched filter coefficients whose PSRs have the maximum value and SNR loss has the minimum value.

  To find N-bit binary sequences for matched filter whose PSLs or ISLs have the minimum value we used (14) and (15).

  
  

  coSt = min ( Q_A ( m _ _F ) + Q B ( m _ f ) )

  
  

  = min ( max„_#0

  
  

  +

  
  

  2 £ N Y ² ( n ) ? )) ⁽¹⁴⁾

  
  

  N ²

  
  

  fitness = max ( Q C ( M - F ) + Q D ( M - F ) )

  
  

  = max

  
  

  Г max n = o ( Y ( n )|) _v^ ^maxn _# a ( Y ( n )|)

  
  
  
  
  
  
  

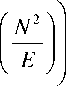
  Table 1. The pseudocode of the GA algorithm

  
  

  To find a mismatched filter with the high PSR value we can use (16).

  
  

  fitness = max ( ^Qs ( Mis _ co ) )

  
  

  = max

  
  

' ^max„ = 0 ( Y ( n )|) ' _v ^maxn _# 0 ( Y ( n )|)_?

V. Simulation Results

The main algorithm to optimize the matched and mismatched filters is shown in Fig 1.

As mentioned before, the output of the matched filter is the auto-correlation function of the input signal. So, a good criterion for choosing bi-phase codes is that their auto-correlation has the sidelobes as minimum as possible. According to the equation (14), (15) and Fig. 1 we search for MPS codes that have minimum values of PSL and ISL. The best codes found, are given in Table 2.

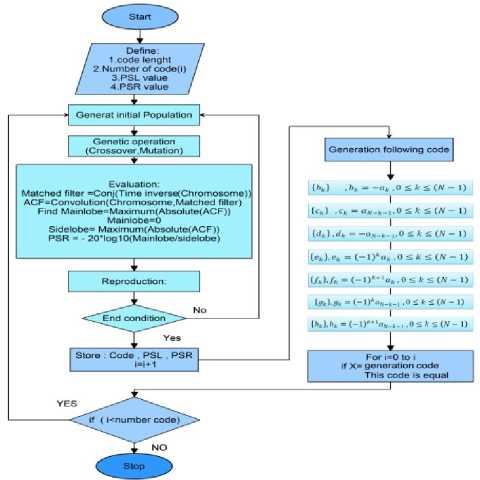
Fig.1. Flow Graph of Innovative Approach using GA

Fig. 1 offers Genetic Algorithm which is an innovative search algorithm used for finding the MPS code with the advantage that the problem of finding equal codes is solved. We used Genetic Algorithm to generate random codes.

The successful extraction of information about the range and velocity is determined by measuring the accuracy of the radar. The performance of the radar system is accurately indicated by the ambiguity function. The response of the matched filter radar receiver to a target displaced in range delay T and Doppler frequency from a reference target as defined by the ambiguity function.[6] Some of filter ambiguity functions are shown in Fig. 3. Ambiguity function is determined as (17):

to

IX (T, Ф )= J u (t) u* (t + T ) e-j2 mptdt    (17)

-to

Table 2. Best found BPSK code with Small PSLs and large MFs for 14 to 31code length

Length	PSL	ISL (dB)	PSR (dB)	Code	MF
14	2	-7.1247	16.902	019FA	5.1579
15	2	-6.8942	17.501	6428	4.891
16	2	-6.6005	18.0618	C2DD	4.5714
17	2	-6.5471	18.588	0B381	4.5156
18	2	-8.1158	19.0849	2BC26	6.48
19	2	-6.8828	19.5545	0EEDA	4.8784
20	2	-7.2125	20	5181B	5.2632
21	3	-8.1193	20.4238	9447C	6.4853
22	3	-7.9275	17.3060	38D4DF	6.2051
23	3	-7.5033	17.6921	2AD818	5.6277
24	3	-9.0309	18.0618	380AD9	8
25	2	-8.5140	21.9382	7015B2	7.1023
26	3	-8.7570	18.7570	12540E7	7.5111
27	3	-9.9350	19.0849	0F1112D	9.8514
28	2	-8.9432	22.9226	1E2225B	7.84
29	3	-8.3137	19.7055	31FD5B2	6.7823
30	3	-8.8236	20	3F6D5CE	7.6271
31	3	-8.5562	20.2848	7F1CD95A	7.1716

Where u(t) is the transmitted envelope waveform, suitably normalized, positive (t) indicates a target beyond the reference delay, and positive φ indicates an incoming target.

Next, considering the values of Table 3, the ambiguity function for the optimized code is plotted.

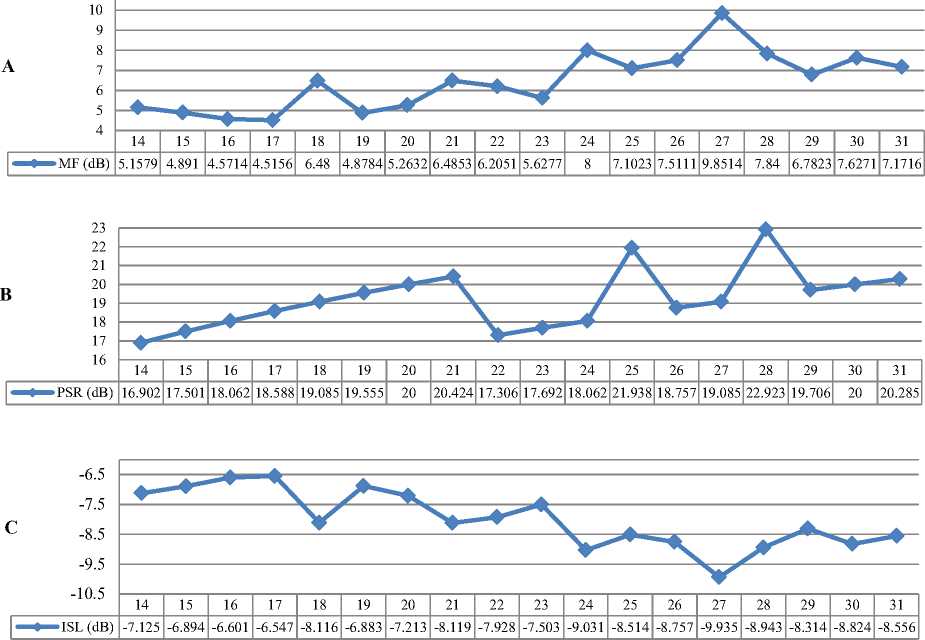
Fig.2. Best Found BPSK Code for 14 to 31code Length Value of (A) MF (B) PSR (C) ISL

Table 3. Parameters to Plot the Ambiguity Function

Parameters	values
Sampling Rate befor M.F	4 Msps
Pulse width	205 µ s
Maximum Velocity	1000(m/s)
Minimum Velocity	100(m/s)
Carrier frequency	780 Mhz
Maximum Doppler Frequency	6.2 KHz
Minimum Doppler Frequency	50 Hz

The value of MF, PSL and ISL for each code is shown in Fig.2.

To increase the peak to sidelob rate of mismatched filter, we used genetic algorithm that its pseudo code is shown in Table 1 and succeeded to generate mismatched filter coefficients, with different lengths and maximum PSR. The optimum mismatched filter coefficients generated for some of the existing codes are shown the Table 2. The PSR values for different filter coefficient lengths are shown in Fig. 4. These generated codes have maximum value of PSR. Some set of generating mismatched filter coefficients are given in Table 4.

To evaluate the performance of binary phase codes existing in Table 2 the ambiguity function was plotted for some of these codes as shown in Fig. 3.

As it is clear from Fig. 3, the found binary phase codes have good performance in presence of Doppler shifts.

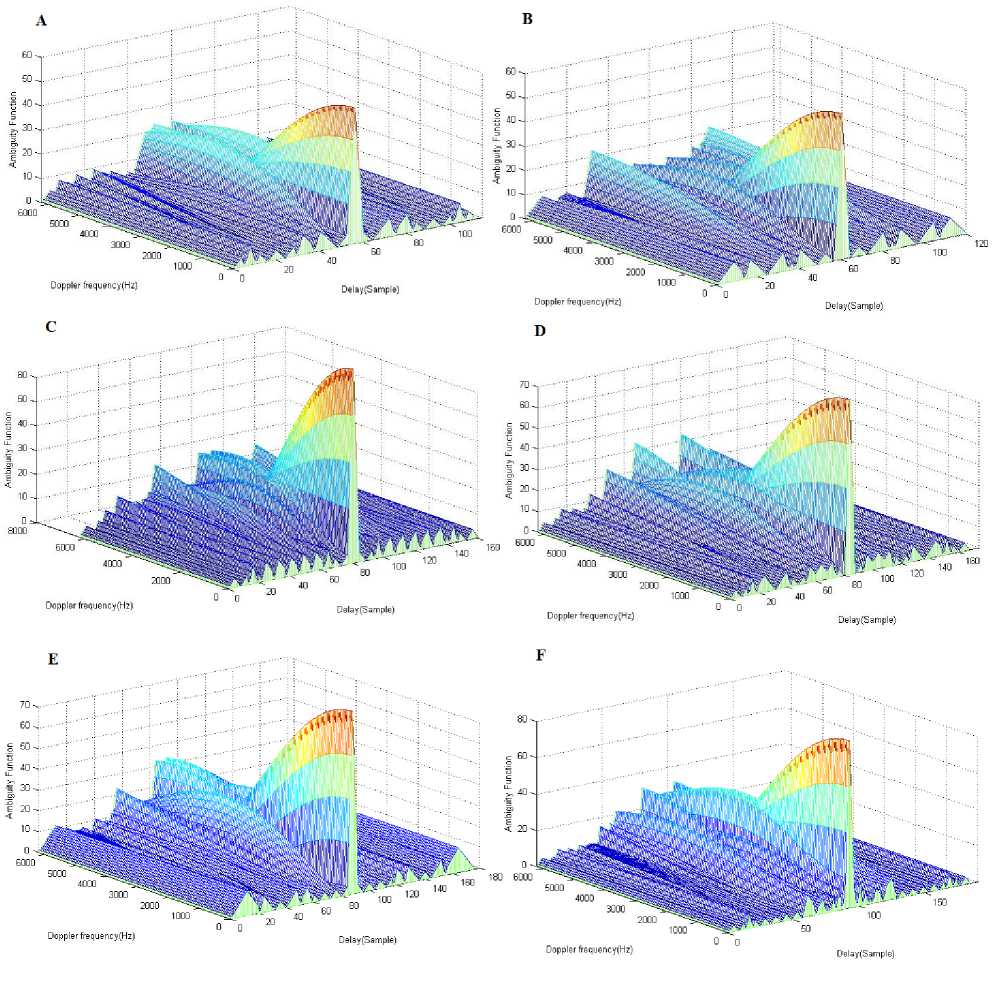
Fig.3. Ambiguity Function of the BPSK code (A) 14-Elements (B) 15-Elements (C) 20-Elements (D) 21-Elements (E) 22-Elements (F) 23-Elements

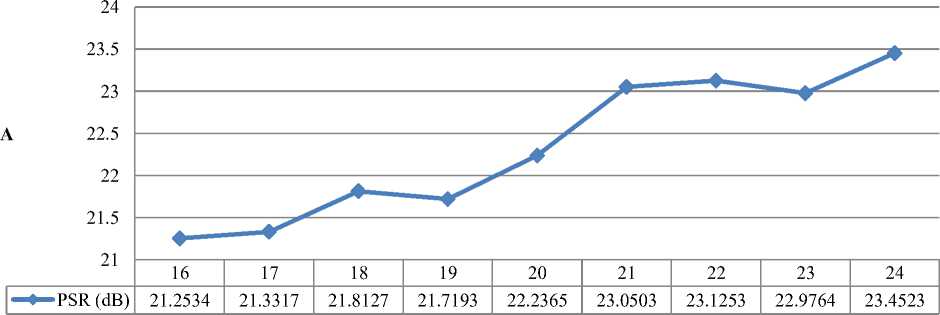
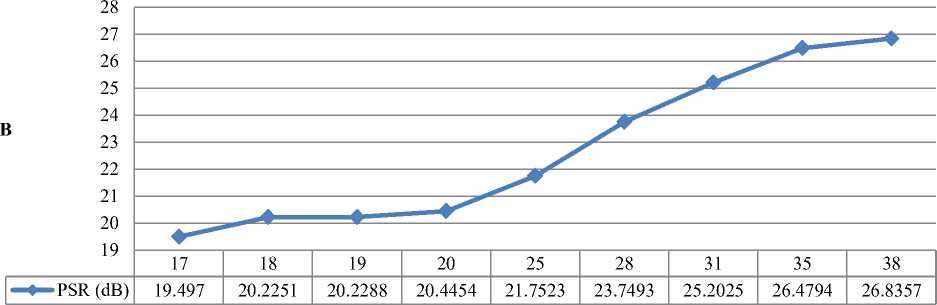
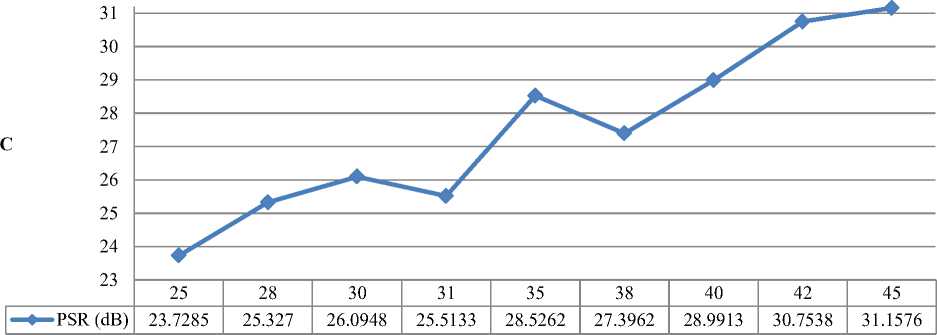
Fig.4. Best Generated Mismatched PSR (A) 14-Elements Transmitted Pulse With Minimum 16 And Maximum 24 Coefficients For Mismatched Filter (B) 15-Elements Transmitted Pulse With Minimum 17 and maximum 38 coefficients for mismatched filter (C) 21-element transmitted pulse with minimum 25 and Maximum 45 Coefficients For Mismatched Filter

Table 4. 3 of Best Generated Mismatched Coefficients

length

Mismatched filter coefficients

21/42

0.622, 0.8582, -0.8682, -0.0529, 2.7604, -0.1878, 1.0262, -0.5437, 1.7051, 2.2593, 0.7342, 4.3455, -3.8429,5.6113,5.1816,-2.4478,6.0784,-2.5792 ,5.2353, 5.4747, 4.662, -3.9209, 2.3677, 6.5386, 4.4641, -3.9132,-2.9193,-2.8904,-3.8566,-2.8541,3.293 ,3.2979,-0.4137 ,-0.7456, 0.3092, -0.1542 ,-0.4711, 1.1773, 1.6169, -0.125 0,-1.0538,-0.2509

-0.358, -0.9795, -0.5454, -0.8849, -1.8934, 1.1999, 2.9322, -1.2431, -0.5967, 3.188, 0.1583, -1.4407, 1.4237, 15/35        -1.2211, -2.185, 1.4861, -5.9708, -7.6379, 6.6725, 4.7676, -5.7129, 6.2525, 6.1321, 3.0117, 6.1759, -4.8769,

1.9926, -3.0696, 4.3211, 0.9422, 2.4236, -0.9082, -0.2956, -0.5084, 0.8794

14/22

-0.0369, 2.6939, -0.38, -0.9704, -1.6966, -2.2123, 4.5541, 6.1841,-4.7356, -5.1341, 2.5278,2.6721, 4.8746, 4.6415, 2.0081, 2.89, -4.1853, 3.3412, -3.9702, 1.3273, -1.8775, -0.3433

To evaluate the performance of mismatched filter coefficients existing in Table 4, the ambiguity function was plotted as shown in Fig. 5.

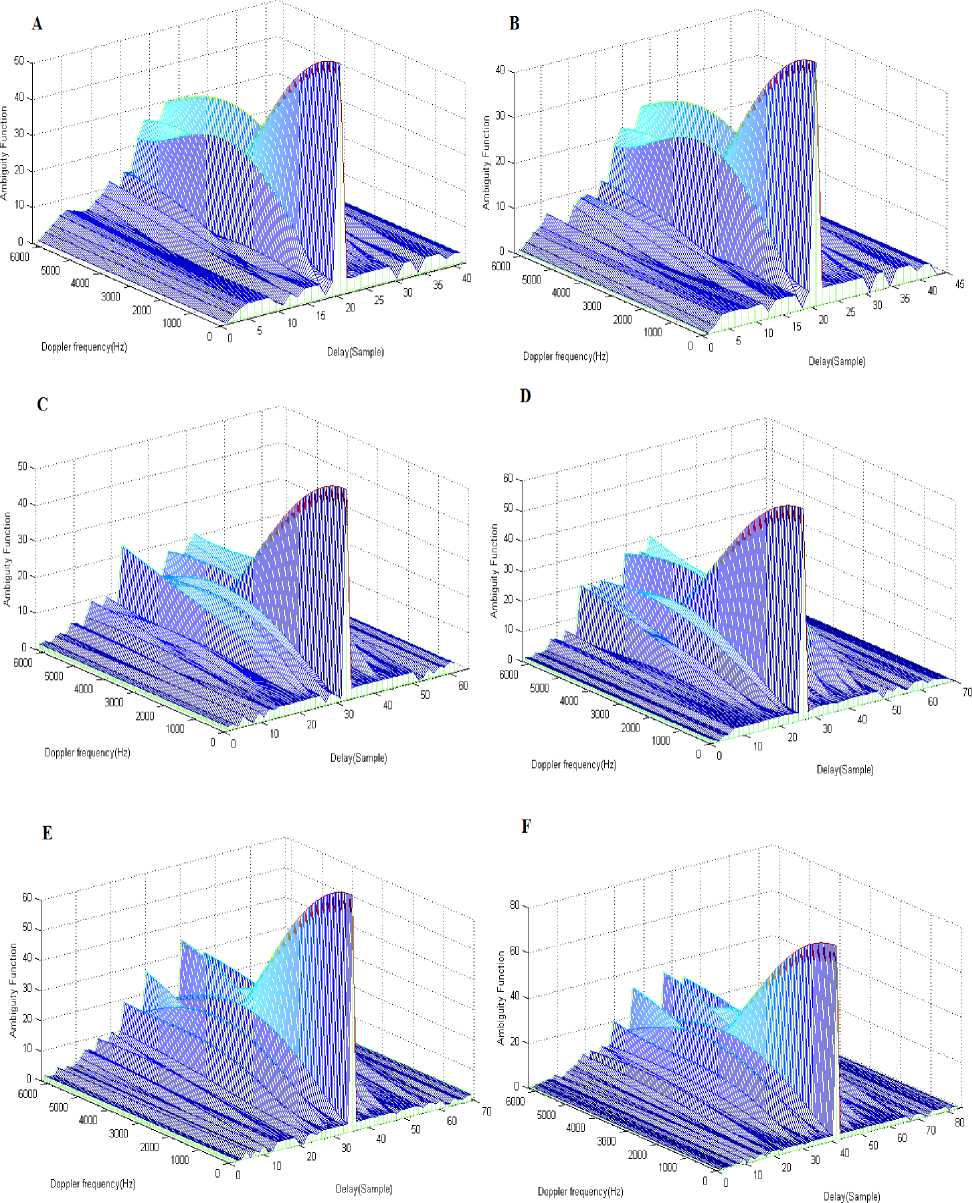
Fig.5. Ambiguity Function of the Mismatched Filter (A) 14/21 Cross-Correlation Function (B) 14/22 Cross-Correlation Function(C) 15/31 CrossCorrelation Function(D) 15/35 Cross-Correlation Function(E) 21/35 Cross-Correlation Function(F) 21/42 Cross-Correlation Function

• VI. Conclusions

In this paper, we considered the problem of high sidelobe levels in the output of the correlation function of matched filter. By using Genetic Algorithm, we found binary phase codes with minimum sidelobe levels which are presented in Table 2. To evaluate the performance of binary phase codes, the ambiguity function was plotted for these codes as shown in Fig. 3. To raise the peak to sidelobe rate of Mismatched Filter, we used Genetic

Algorithms in order to generate filter coefficients. We could generate mismatched filter coefficients with different lengths and maximum PSR for binary phase codes. To test this, using the values mentioned in Table 3, the ambiguity functions are plotted and shown in Fig. 5. Performance of this filter in presence of Doppler shift is acceptable.