Optimization of SVM Multiclass by Particle Swarm (PSO-SVM)

Published Online December 2010 in MECS

Our aptitude to be learned enables us to adapt to our environment, and to progress. It is thanks to this aptitude that humanity owes its survival and its greater successes.

With the rise of Data processing, the pattern recognition experienced a great development. It constitutes a whole of data-processing techniques of representation and decision making it possible the machines to simulate a significant behavior.

Today, the training is a branch of the Artificial Intelligence. The algorithms and the techniques which it knew to develop with the passing of years, find nowadays of the practical applications in a number growing of fields such as the voice recognition (RAP).

Among these algorithms we used the separators with vast margin for their performances in the supervised training and classification nonlinear.

In recent years, population-based optimization algorithms have attracted a lot of attention [1].

Particle Swarm Optimization (PSO) is a new evolutionary computation technique in which each potential solution is seen as a particle with a certain velocity flying through the problem space. Support Vector Machine (SVM) classification is an active research area which solves classification problems in different domains. Basically, SVM operates a linear separation in an augmented space by means of some defined kernels satisfying Mercer’s condition. These kernels map the input vectors into a very high dimensional space, possibly of infinite dimension, where linear separation is more likely. Then, a linear separating hyper plane is found by maximizing the margin between two classes in this space. Hence, the complexity of the separating hyper plane depends on the nature and the properties of the used kernel [2].

This paper proposes hybrid approach which combines support vector classifier with particle swarm optimization, in order to improve the strength of each individual technique and compensate for each other’s weaknesses. This hybrid technique is used to classify the benchmark datasets with SVM kernel: Radial Basis Function (RBF).

10-fold cross validation is used to measure the classification evaluation on the datasets.

The study is organized in the following way: after a short introduction the second section we present the evolutionary method PSO (Particle Swarm Optimization). The third section is devoted to the formulation of a method of classification containing cores to knowing, the machines with vectors of support (SVM). The fourth section we describe in details our contribution PSO-SVM. In the fifth section we expose the results of our experiments. Our work is completed by a conclusion where are put forward the advantages and the weaknesses related to the use of our system.

• II.    Particle Swarm Optimization (PSO)

Particle Swarm Optimization is an evolutionary computation technique proposed by Kennedy and Eberhart. It is a population based stochastic search process, modeled after the social behavior of a bird flock [3, 4]. It is similar in spirit to birds migrating in a flock toward some destination, where the intelligence and efficiency lies in the co-operation of an entire flock [5]. PSO algorithms make use of particles moving in an n-dimensional space to search for solutions for n-variable function optimization problem. All particles have fitness values which are evaluated by the fitness function to be optimized, and have velocities which direct the flying of the particles. The particles fly through the problem space by following the particles with the best solutions so far. PSO is initialized with a group of random particles (solutions) and then searches for optima by updating each generation. The basic structure of PSO is given in Fig.1.

The algorithm can be viewed as a set of vectors whose trajectories oscillate around a region defined by each individual best position and the best position of some other individuals. There are different neighborhood topologies used to identify which particles from the swarm can influence the individuals. The most common ones are known as the gbest and lbest.

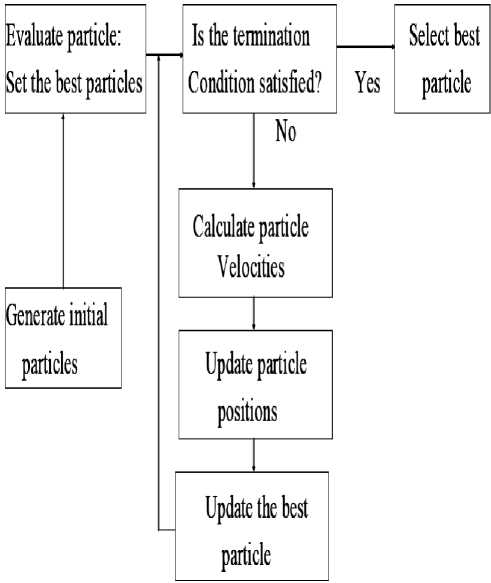
Figure 1. The basic structure of PSO

In the gbest swarm, the trajectory of each individual (particle) is influenced by the best individual found in the entire swarm. It is assumed that gbest swarms converge fast, as all the particles are attracted simultaneously to the best part of the search space. However, if the global optimum is not close to the best particle, it may be impossible for the swarm to explore other areas and consequently, the swarm can be trapped in a local optima [6].

In the lbest swarm, each individual is influenced by a smaller number of its neighbors. Typically, lbest neighborhoods comprise of two neighbors: one on the right side and one on the left side (a ring lattice), this type of swarm will converge slower but can locate the global optimum with a greater chance. lbest swarm is able to flow around local optima. Sub-swarms being able to explore different optima [7].

Figure 2. Graphical representation

A. PSO for Feature Selection

PSO is particularly attractive for feature selection in that particle swarms will discover the best feature combinations as they fly with-in the problem space.

Their goal is to fly to the best position. Over time, they change their position, communicate with each other, and search around the local best and global best position. Eventually, they should converge on good, possibly optimal, positions. It is this exploration ability of particle swarms that should better equip it perform feature selection and discover optimal subsets[8].

• III.   Support Vector Machine

The aim of support vector classification is to device a computationally efficient way of learning good separating hyperplanes in a high dimensional feature space [9]. Support Vector Machine is a Learning Machine proposed by Vapnik et al., [10, 11] which finds an optimal separating hyperplane. It uses a linear hyperplane to create a classifier with a maximum margin [12]. The algorithm aims to find support vectors and their corresponding co-efficients to construct an optimal separating surface by the use of kernel functions in high dimensional feature space[13].

Consider the two-class problem where the classes are linearly separable. Let the dataset D be given as (x1, y1), (x2, y2)….. (xd, yd), where xi is the set of training tuples with associated class labels, yi. Each yi can take one of the two values, either +1 or -1.

The data are linearly separable because many number of straight lines can separate the data points into two distinct classes where, in class 1, y=+1 and in class 2, y= -1. The best separating hyperplanes will be the one which have the maximal margin between them. The maximum margin hyperplane will be more accurate in classifying the future data tuples than the smaller margin. The separating hyperplane can be written as in (1)

w .x + b = 0               (1)

Where, w is a weight vector and b is a bias (scalar).

The maximal margin is denoted mathematically by the formula as in (2)

M

I W II

Where, ||w|| is the Euclidean norm of w.

The maximal margin hyperplane is a linear class boundary and hence the corresponding SVM can be used to classify linearly separable data and such trained SVM is known as linear SVM.

Using Lagrangian formula, the maximal margin hyperplane can be rewritten as the decision boundary for the classification of test or new tuples as given in (3)

l

d (xT ) = ∑ yiaixT + b0               (3)

• i = i

Where, y_i is the class label of support vector x_i ,

. x^T is a test tuple,

. α i is a Lagrangian multiplier,

. b o is a numeric parameter,

. l is the number of support vectors.

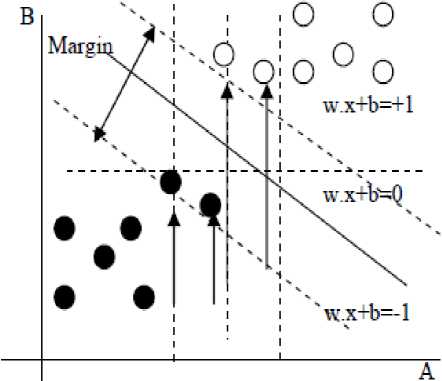
Support Vectors

О - Class l,y=+l Ф - Class?, y=-l

• Figure 3. Linearly separable data

For linearly separable data, the support vectors are the subset of actual training tuples. This equation tells us on which side of the hyper plane the test tuple xT falls. If the sign is positive, then xT falls on or above the maximal margin hyper plane and SVM predicts that xT belongs to class +1. If the sign is negative, then xT falls on or below the maximal margin hyper plane and the class prediction is -1.

SVMs are less prone to over fitting because the classifier is characterized by the number of support vectors rather than the dimensionality of the data. The number of support vectors found can be used to compute an upper bound on the expected error rate of the SVM classifier. Good generalization can be achieved by having SVM with small number of support vectors irrespective of the dimension of the dataset [14].

• A.    Kernel functions

Kernel based learning methods consists of a kernel function to generate a kernel matrix for all patterns.

Entries of kernel matrix are the dot product of pairs of patterns. Kernel matrix generation is of two types.

In the first type, mapping or image of each pattern in a high dimension feature space is generated through construction and combination of features to form a kernel matrix based on the inner products between all pairs of images. In the second method, kernel matrix is constructed by kernel functions which takes two patterns as arguments and outputs a value. This method is known as kernel trick. Each kernel function can derive multiple instances of kernel matrices by varying kernel parameters [15].

A kernel function is a function k(x,y) with Characteristic

κ (x, y) = <φ(x).φ(y)>                        (4)

The dot / linear kernel k(x,y)=x.y is the most simple kernel function. The decision function takes the form kernel function. The decision function takes the form

f (x) = ω.x + b            (5)

RBF kernels takes the form

K(x, x′) = e-γ x-y 2

In this method, the similarity of two examples is judged by their Euclidian distance [16]. In RBF, the number of support vectors, the weights and the threshold are all produced automatically by an SVM training algorithm and yield excellent results.

• B.    Multiclass Extensions

Support Vector Machines are inherently binary classifiers and its efficient extension to multiclass problems is still an ongoing research issue [17,18,19]. Several frameworks have been introduced to extend SVM to multiclass contexts and a detailed account of the literature is out of the scope of this paper. Typically multiclass classifiers are built by combining several binary classifiers. The earliest such method is the One-Against-All (OVA) [20,17] which constructs K classifiers, where K is the number of classes. The k th classifier is trained by labeling all the examples in the k th class as positive and the remainder as negative. The final hypothesis is given by the formula:

fova(x)=argmaxi=1, ,k(fi(x))      (7)

Another popular paradigm, called One-Against-One

(OVO), proceeds by training k(k-1)/2 binary classifiers corresponding to all the pairs of classes. The hypothesis consists of choosing either the class with most votes (voting) or traversing a directed acyclic graph where each node represents a binary classifier (DAGSVM) [18]. There was debate on the efficiency of multiclass methods from statistical point of view Clearly, voting and DAGSVM are cheaper to train in terms of memory and computer speed than OVASVM . [19] investigated the performance of several SVM multi-class paradigms and found that the one-against-one achieved slightly better results on some small to medium size benchmark data sets.

• C.    Implementation of SVM for Phonetic Classification

SVM using standard kernel cannot deal directly with variable length or sequential data such as speech patterns. Early implementations attempted to incorporate dynamic information by a hybridization with HMM [21]. In [22], a novel kernel based on Fisher score was introduced and the authors report some positive results. An interesting implementation of SVM for speech patterns which performs frame wise classification was studied in [23]. It is worthwhile mentioning here that this approach has the advantage of not using phoneme boundaries information and at the same time it can be implemented with standard kernels. However, the size of the training set produced by this method is huge and the authors were forced to use only a portion of the data set for training. They estimated six years of CPU training time for the full TIMIT set. [24]

Implemented SVM for phonetic classification by using a 3-4-3 rule for producing a fixed-length feature vector from the MFCCs.

The authors report an unusually high recognition rate which we were not able to reproduce. Finally, [25] used linear RLSC for the classification of TIMIT phonemes.

• D.    Variable windowstep feature extraction for kernel methods

As discussed earlier, standard MFCC are extracted for 25 milliseconds Hamming windows and 10 milliseconds overlap (Fig.4). The feature vector obtained is of dimension 12 plus an energy term. The TIMIT data set contains over 1 million examples if we perform frame wise classification

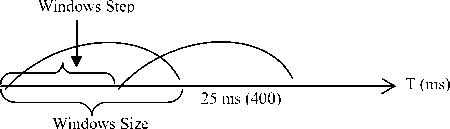
Figure 4. Windows

In order to keep the size of the training set tractable for kernel methods and take into account the speech dynamics, a natural approach would be to keep the window size fixed and set the window step according to the duration of the phoneme. The window step length can be computed as:

WindowsStep= (Length (Input) - WindowsSize)/ nF

Where nF stands for the average number of frames. In our experiments nF was set to 5 resulting in feature vectors of dimension 65 and no derivatives were added.

fits better than its predecessor. This process continues until the performance of SVM converges [26].

PSO is used to find optimal feature subsets by discovering the best feature combinations as they fly within the problem space from the processed datasets.

The procedure describing proposed PSO-SVM approach is as follows.

• 1.    Initializing PSO with population size, inertia weight and generations without improval.

• 2.    Evaluating the fitness of each particle.

• 3.    Comparing the fitness values and determine the local best and global best particle.

• 4.    Updating the velocity and position of each particle till value of the fitness function converges.

• 5.    After converging, the global best particle in the swarm is fed to SVM classifier for training.

• 6.    Training the SVM classifier.

The PSO-SVM takes the advantage of minimum structural risk of SVM and the quick global optimizing ability of PSO.

The application of the algorithm of optimization by particulate swarm, like any evolutionary algorithm, is influenced by factors such as the criterion of stop, the structure of particle, the objective function.

Criterion of stop: The criterion of stop can be an iteration count attached to the precondition, a value of function objectifies reached or a movement of the particles close to the zero.

The structure of the particles: A particle " I " will contain a vector representing contains two values (a value for the coefficient of regularization " C " and a value for the parameter of core RBF "sigma ") such as the position x ij = (x i1 , x i2 ).

The objective function: The purpose of the function objectifies will be to reduce the error of generalization to the minimum.

• IV.    Optimization of the SVM by PSO

In this section, we describe the proposed PSO-SVM system for classification. This study initially aims at optimizing the accuracy of SVM classifier by detecting the subset of best informative features and estimating the best values for regularization of kernel parameters for SVM model. In order to achieve this PSO based optimized framework is used. PSO-SVM algorithm combines two machine learning methods by optimizing the parameters of SVM using PSO.

PSO starts with n-randomly selected particles and searches for the optimal particle iteratively. Each particle is a m-dimensional vector and represents a candidate solution. SVM classifier is built for each candidate solution to evaluate its performance through the cross validation method. PSO algorithm guides the selection of potential subsets that lead to best prediction accuracy. The algorithm uses the most fit particles to contribute to the next generation of n-candidate particles. Thus, on the average, each successive population of candidate particles

• V.    Implementation Details and Experimental Results

In our experiments with the variable window step feature extraction framework, we performed our experiments on the TIMIT [27] corpus. The 61 labels were collapsed to 39 prior to scoring as in [25]. When indicated by “si-sx”, we used only the “si” and “sx” sentences. For TIMIT vowels we used the set : {[aa], [aw], [ae], [ah], [ao], [ax], [ay], [axr], [ax-h], [uw], [ux], [uh], [oy], [ow], [ix], [ih], [iy], [eh], [ey], [er]}.

To evaluate the performance of the algorithms, several measures have been employed in our work. 10fold cross-validation is the standard way of measuring the accuracy of a learning scheme on a particular dataset. The data is divided randomly into 10 parts in which the class is represented in approximately the same properties as in full dataset. During each run, one of partitions is chosen for testing, while the remaining nine-tenths are used for training. Again, the procedure is repeated 10 times so that each partition is used for training exactly once. Classifier performance is also evaluated by calculating the ratio of ratio of number of correctly classified instances to total number of instances (Accuracy).

Paramétres fixed for PSO: we applied algorithm PSO by fixing the parameters W, c1 and c2 with the values given in the literature [30][31 ] such as W = 0.75, c1= c2= 1.5 and numbers it particles with 30, the iteration count to 100.

As regards topology vicinity, we chose a vicinity 'gbest' which ensures one converges faster than the model ' lbest' [28][29 ].

The set 18 phonemes is a subset of 18 labels handpicked from the 61 labels. All the experiments were run on standard Pentium IV 2.66 GHZ with 256 Meg memory running the Windows XP operating system.

In this section, we compare the results obtained by method SVM and our system PSO-SVM on the various corpora considered by using the approach multi-class One-vs-one. We start initially by determining the good parameters ”C " and " sigma ", in order to use the benchmark datasets with the good values obtained.

The following tables summarizes our results:

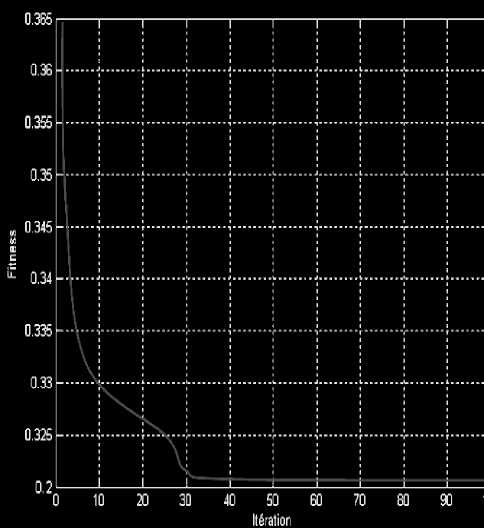
Figure 5. Evolution of the fitness during generations (corpus 39-Classes)

It is as important to note as the passage from 10 to 30 particles increased the rate of recognition (fig. 6).

TABLE I

RESULTS FOR 18 PHONEMES.

	Accuracy (%)	#SV	CPU Time
PSO-SVM	86,45	21594	2655,80
SVM	84,18	17667	6482,77

TABLE II

RESULTS FOR 39 CLASSES.

	Accuracy (%)	#SV	CPU Time
PSO-SVM	86,50	109347	512587,05
SVM	76,62	101184	584970,41

TABLE III

RESULTS FOR 20 TIMIT VOWELS.

	Accuracy (%)	#SV	CPU Time
PSO-SVM	55,38	35099	792,53
SVM	60.14	40468	504.00

TABLE IV

RESULTS FOR SI-SX 39 CLASSES.

	Accuracy (%)
PSO-SVM	69.04
SVM	69.20

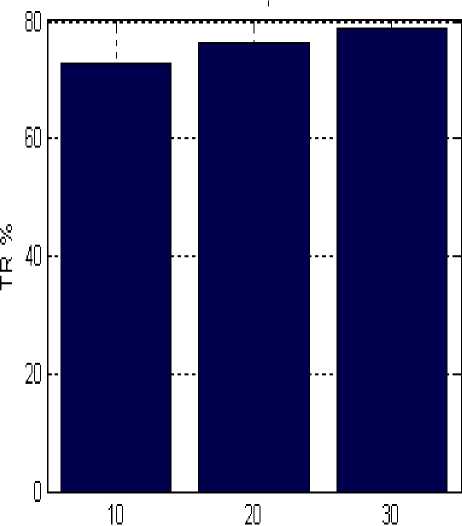
Figure 6. Results obtained by PSO-SVM (Approach Multi-class one-Vs-one)

The figure “fig.5” shows a curve which was obtained on the corpus 39-Classes and which represents the fitness during the thirtieth generations. One initially sees there a fast reduction in the fitness until A the generation, and after this iteration, one notices a stability of the fitness, which shows that the total convergence of the population is carried out.

• VI.    Conclusion

This paper proposes a PSO-SVM technique to optimize the performance of SVM classifier. 10-fold cross validation is applied in order to validate and evaluate the provided solutions. The results obtained show that approach PSO-SVM gives a better classification in terms of accuracy even though the execution time is increased.