Optimization of Value of Parameters in Ad-hoc on Demand Multipath Distance Vector Routing Using Magnetic Optimization Algorithm

Published Online November 2015 in MECS

Vehicular ad-hoc network (VANET.) is formed by interconnection of moving vehicles. The moving vehicles are equipped with on-board systems which help to communicate with other vehicles coming into transmission range. VANET can provide driving assistance by using the information regarding traffic, collected through the communication among the vehicles. During the communication, frequent disconnection takes place because of changing topology. Therefore, the routing protocols designed for VANET must deal with the frequent disconnections for delivering the messages. Researchers in the area have proposed many routing protocols as reported in the literatures. These protocols which are based on their nature of working are divided as proactive and reactive. Proactive routing protocols (table driven protocols) are those which keep a path between the source and destination ready all the time for communication before a source wishes to send the message. Destination Sequenced Distance Vector (DSDV), Optimized Link State Routing (OLSR) etc., is examples of proactive routing protocols. Reactive routing protocols (on demand routing protocols) try to establish a path when the source is required to send the message to the destination. AODV, DSR etc are examples.

It has been observed that most of the VANET applications critically rely on routing protocols. The performance of these protocols depends on the parameter value used for evaluation [1]. Therefore, the techniques that can determine the optimal value of parameters for the protocol may be used before deployment. Optimal value of parameters improves the Quality of service (QoS) in VANET. In this paper, we have defined a strategy that solves the problem of determining the optimal value of the parameter to improve the QoS. We have chosen for Ad-hoc on demand multipath distance vector routing protocol (AOMDV) [2] since it has many features. One of features is that it keeps communicating via an alternate path available when there is a link breakage between source and destination. AOMDV presents reduced end-to-end delay and increased PDR as compared to AODV.

The control packets used in the protocols create congestion and depend on the value of the parameters. Therefore, we have used meta-heuristic for finding the optimal value of parameters. Meta-heuristic is used to solve the optimization problem in many other areas of engineering.

An optimization problem is defined in terms of the search space, i.e. the number of possible solutions (also known as solution vector). There are nine parameters in the AOMDV which are responsible for the performance of VANET and each parameter has some specified range. Therefore, the possible combinations of the parameters value are large and finding the optimal value of the parameters in the search space is a very complex task. This problem is also known as a combinatorial optimization problem.

In this paper, we are going to find an optimal value of parameters for AOMDV protocol on VANET using Magnetic Optimization algorithm (MO). This algorithm (MO) is chosen since its principle of working is inspired by the magnetic field theory. Therefore, particles, even the worst ones, attract their neighbours in the search space based on their magnetic field [3]. Moreover, the important characteristic of MO, which makes it a good solver of combinatorial optimization, is that it does not prematurely converge which leads to local optimal solution [4]. The network simulator, ns-2 [5], is used as a fitness function evaluator. It gets the value of parameters provided by MO, and evaluates them to guide the MO in the search space for finding the tentative optimal value of parameters. A real scenario map of Noida sector 63, U.P., India has been taken so that the evaluation of AOMDV using MO may become more realistic. This scenario has been generated by downloading a real map using Java OpenStreetMap editor [6] and converted into a form which is supported by SUMO [7].

In summary, the main contributions of this paper are as follows:

• •    We have proposed a strategy to evaluate the performance of AOMDV.

• •    Mapping of problem in MO.

• •    We obtain the optimal value of parameters for AOMDV, which outperform the default value or human expert given values of parameters (standard values).

• •    We generate a set of realistic VANET scenarios based on real map of Noida 63 UP India.

Optimal value of parameters determined has shown better QoS as compared to the default value of parameters or the human expert given value of parameters. The remainder of the paper is organized as follows. In section II, related work is discussed. In section III, an overview of the problem has been discussed. Section IV consists of a framework of the optimization strategy. Section V discusses about mapping of problem in MO. Section VI tells about VANET Scenario and Mobility Models used. Section VII illustrates the experimental set up and result analysis. Finally, section VIII gives the conclusion and future directions of research work that can be carried out in this area.

• II.    Related Work

In this paper, we are using MO, a meta-heuristic to find optimal value of parameters in AOMDV. The nature of the problem is combinatorial optimization problem. The different optimization techniques have been used to solve the similar combinatorial optimization problem in a multitude of engineering disciplines but very limited applications of meta-heuristic are observed in ad-hoc networks, especially in VANETs. Some of the applications are mentioned as follows.

The problem in mobile ad-hoc network (MANET) is its broadcast strategy to disseminate the message in its network formed by mobile nodes. Broadcasting in MANET deals with three issues, first reaching as many stations as possible, second minimizing the network utilization, and third reducing the make span. These three issues have vital impact on the performance of MANET. Therefore, Ref. [8] deals with fine tuning of broadcast strategy using a cellular multi-objective genetic algorithm (cMOGA). Ref. [9] solves network partitioning problem in mobile multi hop ad-hoc network using six version of Genetic Algorithm. It works by optimizing injection network. Injection networks come into existence when two networks are connected by long range links which is called bypass links. Here, bypass link is optimized which consequently, optimizes the injection network. Ref. [10] explains the strategy to find optimal configuration for AODV protocol before deployment in the VANET. It requires because the performance of VANET critically depends on the protocol being used in. This strategy uses five meta-heuristic algorithms- Particle Swarm Optimization (PSO), Simulated Annealing (SA), Differential evolution (DE), Genetic Algorithm (GA) and Evolutionary Strategy (ES). The experimentation conducted shows PSO outperform all other algorithms. Using the same strategy, Optimized Link State Routing (OLSR) is tuned [1]. The meta-heuristic used are PSO, DE, SA and GA. In Ref. [11], dynamic Quality-of-Service (QoS) multicast routing problem is solved using genetic algorithm with immigrant schemes. Number of mobile nodes change dynamically in network and in such scenario different multicast trees is formed. Which multicast tree is optimal is investigate in the approach. In Ref. [12], a novel QoS routing algorithm based on ant colony optimization is proposed. The experimental results exhibit that proposed algorithm shows better packet delivery Ratio, end to end delay and network life time. In Ref. [13], file transfer service in realistic VANET scenarios, is optimized by using different meta-heuristics. This approach uses PSO, DE, SA and ES to optimize the transmission time, amount of data transferred and the number of lost packets in realistic VANET scenarios.

• III.    Problem Overview

In VANET, the communication between a source and a destination takes place through multiple hops. The primary aim of communication is routing of messages. At run time, a path is established through multiple moving vehicles. If a vehicle moves out of communication range of another vehicle in the path, it results in disconnection of the path. For establishing and maintaining paths, vehicles (nodes) send or receive control packets. As the number of control packets increases, it affects QoS in VANETs. The control packets depend on the value of parameters used in the deployed protocol in VANET. Here, we have taken AOMDV protocol to deploy and test using MO. The reason to choose AOMDV in VANET is due to its multiple features.

• A.    AOMDV

AOMDV is an extension of Ad-hoc on demand distance vector routing (AODV) [14] protocol. It has used the same basic approach used in distance vector and hop-by-hop routing [2]. It also uses the same route discovery procedure as in AODV. But the basic difference between these two protocols lie in number of paths found. In AOMDV multiple, disjoint, loop free paths are discovered wherein AODV, a single path is discovered between a source and a destination pair. Another important difference is that AOMDV starts the route discovery process when all discovered routes fail. Since, multiple paths exist which causes to perform fewer route discoveries [15], as a result packet loss is reduced by 40%, routing overheads by 30% and significant improvement has been seen in end to end delay [2].

The AOMDV works in a similar manner as AODV by using the four message sets. First, route request (RREQ) message is used to find routes from a source to destination. To accomplish this AOMDV performs route advertisement and route acceptance which are not performed in AODV. The route advertisement and route acceptance [15] help protocol in maintaining freedom from loops in paths. Second, Route reply (RREP) is one of the messages used to reply to the source from the destination or from an intermediate node, having a fresh path, from the node to the destination. Third, the route failure is notified by a route error (RERR) message. The last one is link status monitoring that is done by exchanging HELLO message. There would be many paths found during the route discovery process but only disjoint paths are considered. As, AOMDV has been extended from AODV with some additional functions as discussed above, all other parameters of AODV remain same in AOMDV. The parameters and their default values, mentioned in Table 1 are taken from AODV (RFC 3561) [14] and used in AOMDV to optimize the value of these parameters.

• B.    Parameter Tuning

  The default value of parameters used in AOMDV offer moderate QoS. Therefore, considering the impact of value of parameters on the network performance, we try to discover an optimal value of parameters for AOMDV before deployment. There are nine parameters used in AOMDV as mentioned in Table 1. As it can be seen from Table 1, the number of possible combinations of the value of parameters would be very large (10¹¹ sets). Further, testing of each set of parameters on ns-2 individually is impractical. This motivates us to use the meta-heuristic that is capable to solve the combinatorial optimization. The range of parameters given in Table 1 is considered based on the restrictions posed in AOMDV.

To analyze the different sets of parameters value (solution) we have used three well known QoS parameters, Packet Delivery Ratio(PDR), Average End-to-end Delay(AE2ED) and Normalized Routing Loads (NRL) as defined in [10, 16]

• •    PDR – This is the ratio of the number of packets received at the destination and the number of packets sent by the source.

• •    AE2ED – This is average time duration taken by a packet in transmission from a source to a destination.

• •    NRL – This is defined as the ratio of administrative routing transmission and data packets delivered. Here, transmission counting is done by counting each hop separately.

  Table 1. AOMDV Parameter and its Default Values-Extended from AODV (RFC-3561)

  Parameter	Default   Values	Range
  ACTIVE_ROUTE_TIME _OUT	3.0S	1 to 10
  ALLOWED_HELLO_LOSS	2 HELLO Packets	1 to 10
  MY_ROUTE_TIMEOUT	2 × ACTIVE_ROUTE_TIME _OUT	1 to 10
  NET_DIAMETER	35 Nodes	1 to 50
  NODE_TRAVERSAL_TIME	0.04 s	0.01 to 1.00
  RREQ_RETRIES	2 tries	1 to 10
  TTL_START	1.0 s	1 to 10
  TTL_INCREMENT	2.0 s	1 to 10
  TTL_THERSHOLD	7.0 s	1 to 20

  
  

• IV.    Framework of Optimization

The framework of optimization consist of two parts -optimization algorithm and solution evaluation as shown in Fig. 1. In optimization algorithm, a new set of parameter values (solution) is generated by MO and used to find an optimal set of parameter values in the search space (solution vector). This optimization is carried out using a fitness function mentioned in equation (1). The simulation model accepts the set of parameter values from MO and passes it into AOMDV. Now, ns-2 takes VANET realistic instance and configures it according to AOMDV protocol and simulation parameters as mentioned in Table 2. The process of accepting a set of parameter values from MO is done automatically because NS-2 has been modified accordingly. NS-2 produces global information, known as simulation trace.

Solution Evaluation

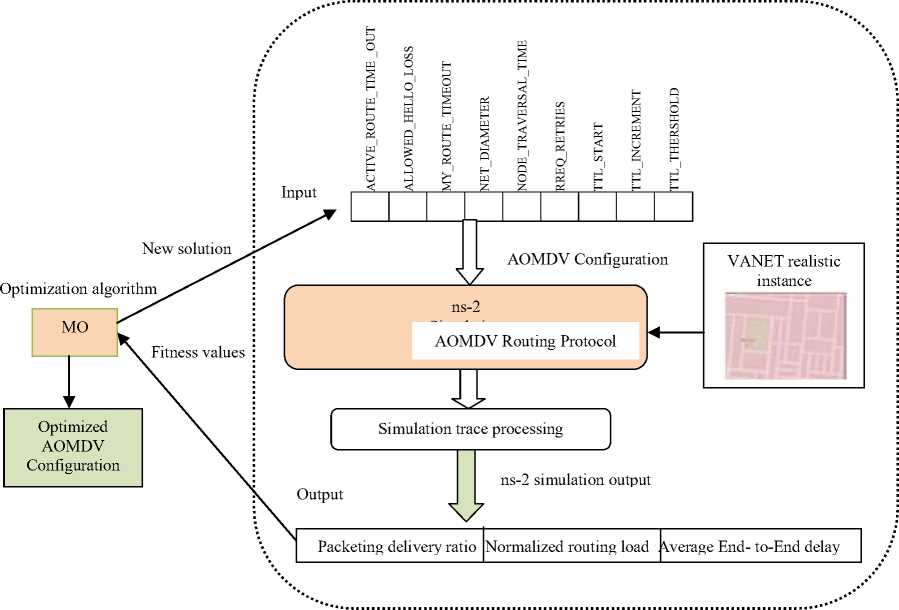
Fig. 1. The optimization framework for AOMDV using MO. MO invokes the ns-2 simulator for each solution evaluation

This information is used to calculate the QoS (PDR, NRL and AE2ED) parameters which are used for calculation of the fitness function. The fitness function is defined as follows [10]:

The objective of this fitness function is to maximize PDR and to minimize both the NRL and AE2ED. Equation (1) is the aggregate minimizing function and that is the reason PDR is used with a negative sign. The w1, w2 and w3 are used to weigh the effect of each QoS parameters on the resultant fitness value. The values of w1, w2 and w3 are taken 0.5, 0.3, and 0.2 respectively in the equation. Therefore, PDR gets priority over AE2ED and NRL. This is because, we are trying to maximize the PDR and minimize others (NRL, AE2ED).

• V.    Problem Mapping in MO

Four basic forces exist in the universe and magnetic force is one of them which are created by the magnetic field [3]. In the magnetic field, a particle having higher mass has a greater magnetic force and therefore, it attracts other particles with smaller mass. The same concept is used in MO. In addition, MO ensures not to converge prematurely in search space [3]. Generally, premature convergence in search space leads to local optimal solution. Therefore, it is suitable to use MO [3] for the proposed problem, and it is modified accordingly. The modified MO is given in Algorithm 1.

Algorithm 1. MO Algorithm

Input: 10 sets of 9 parameters value along with their communication cost is in X as population.

Output: Optimized 10 sets of 9 parameters value.

Begin

• 1:   Initialize X with lattice-like structure.

  2:

  3:

  4:

  5:

  6:

  7:

  8:

  9:

  
  

Evaluate individuals in X and store their profits in a magnetic field B.

Normalize B according to the equation (2).

Evaluate the mass M for all particles using equation (3).

for all particles x i in X do

Begin

F i =0

find Ni for all xu in Ni do

Begin

F =F + ⁽ , k^ , к )× Bu

,          , +       ^, ( , к,x_u,к₎

End

End

• 10:    for all particles xi in X do

Begin

• 11:    vi,к₌   ^, ; ×R(lк,uк)

• 12:    x1, lew =xi,к +vi,к

End

The steps of algorithm 1 are explained as follows:

• 1)    In this step, we pass 10 sets of 9 parameters value along with their communication cost given in X as the population. Therefore, we generate a 9 dimensional search space with l k and u k as the lower and upper bound of the k^th dimension respectively. x i,k denotes the value of k^th parameter of i^th particle where i=1,2,3,...,10. The first population is generated randomly and then the successive populations are obtained by running the algorithm on previous population.

• 2)    Here, the cost of individual solution as their profits is evaluated and stored in B i where i denote one of the 10 sets of the population present in the search space (solution vector).

• 3)    In this step, we perform the normalization of B as given below:

  B=

  
  

  Мах-Bi Max-Min

  
  
  
  

  End

  
  

Where, Min = minimum (B i ) and

Max = maximum (Bi) where i = 1 to 10.

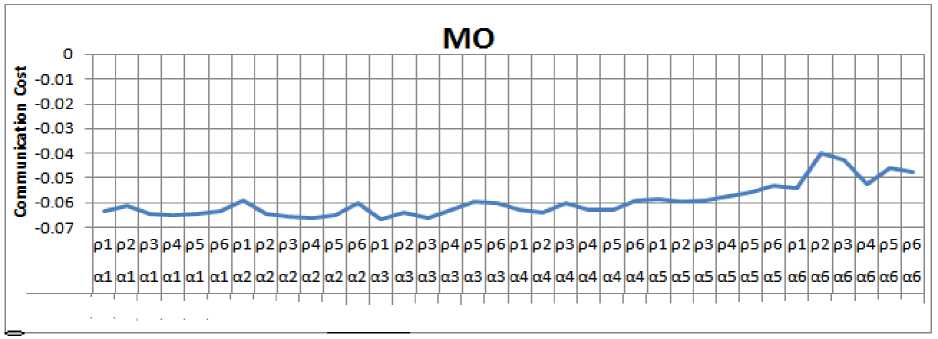
Fig. 2. MO parameters setting The parameters of MO is set to α1, α2… α6 (0.1, 1, 4, 8, 15, 30), and ρ1, ρ2… ρ6 (0.1, 1, 4, 8, 15, 30)

• 4)    The mass of all the particles is calculated and stored in M using following equation

Mi=α+ρ×Bi            (3)

The value of α and ρ are constant as well as problem dependent [3, 10]. The procedure of finding best value of α and ρ for different problems is mentioned [3, 17]. Therefore, we have adopted the same procedure, and used the optimization framework mentioned in Fig. 1 for small map to find best value of α and ρ for proposed problem. The population size is taken 10 and for each combination of α and ρ, MO runs for 25 iterations. Further, the average of minimum fitness value (Communication cost) of all iteration is taken (shown in Fig. 2).

The possible combination of α and ρ values are 36 [3]. We have 36 different average minimum fitness value and among these 36, we get the minimum average on α = 4 and ρ= 0.1 respectively (α3 and ρ1 form Fig. 2). In Fig. 2, all combinations of α and ρ is shown. Any combination out of 36 can be used, but on different combination convergence of MO is affected. Therefore, we want to test the proposed problem on best value of α and ρ in MO.

• 5)  Here, the "for" loop is used to calculate the

resultant force on all the particles.

• 6)  The value of the resultant force (F_i) on each

particle is initialized to zero.

• 7)    This step finds N i which is the set of all the particles that are neighbour of the i^th particle on which the force is to be calculated. Here, we consider that each particle interacts with every other particle in the search space, and therefore each particle applies force on every other particle.

• 8)    This step calculates the force on a particle applied by the other neighbour particles.

• 9)    In this step, force ( F , ) is calculated in using the distance between the two particles. In [3], three methods are mentioned to find the distance between the two particles in the search space. We have used the following equation to calculate the same.

of the VANET instance. Once the evaluation on these positions are over, the new fitness values along with corresponding positions are again passed in MO as shown in Fig. 1. This process is repeated for 50 times to attain the optimal value of parameters for a given scenario.

D(x , ,x ^{) =} m^{∑ |} u ^, - l , s| m    u -l

Here, uk and lk are the upper and lower bounds of kth dimension in the search space and xi,k and xu,k are positions of the ith and the uth particles with respect to kth dimension in the search space.

• 10)    In this step, “for” loop is used to calculate the new positions of all the particles using step 11 and 12.

• 11)    The velocity of the particle is calculated by modifying the formula given in [3].

Fik vi,к=  ,  ×R(lк,uк)

Mi,к

The value of R (l k , u k ) is a random number between (0, 2].

• 12)    The new position of a particle is calculated by the formula:

  x

  
  

  New = i i,к =x ,

  
  

  +vi,к

  
  

• 13)    These new positions (10 sets of solution vector) are then passed to ns-2 for performance evaluation

• VI.    VANET Scenario and Mobility Model

  For carrying out experiments, we have considered traffic/network simulator that can generate traffic movement of vehicles, and communication activity. In the simulation, we have generated a real map of Noida sector 63 UP, India (1068m×1075m area) using Java openstreetmapeditor (A Java based software JOSM) [6]. Generated real map is an osm file. Using netconvert, we have converted this file in a format supported by the SUMO traffic simulator [18].

The map of the area in reference is shown in Fig. 3. On this map, traffic scenario in terms of number of vehicles, connections, turn, and flows is created. This traffic scenario is passed in MOVE [7] simulator to generate TCL script. The TCL script is imported in ns-2 simulator. The parameters used in final ns-2 simulation are listed in Table 2. In the simulation, for data flow model, CBR is used as network application and UDP (user datagram protocol) as source agent in vehicles. CBR packet size of 1000 bytes and bit rate of 64Kb per second is taken. This set of parameters help AOMDV to find and maintain the routes from source to destination.

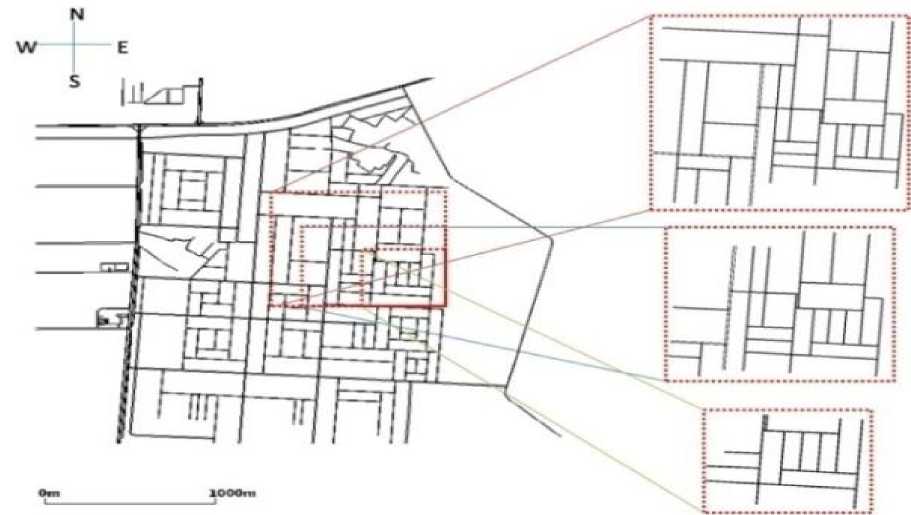
Fig. 3. Noida sector 63, India [19] Real VANET Scenarios. The maximum selected Area is 1068m×1075m

Table 2. Simulation Parameters for VANET

Parameters	Values
	Small Map	Medium Map	Large Map
Simulation time	3 Minutes	3 Minutes	3 Minutes
Simulation area	560X447 m2	873X790 m2	1068X1075 m2
Number of vehicles	10 Vehicles	20 Vehicles	30 Vehicles
Vehicle speed	0-50 km/hr	0-50 km/hr	0-50 km/hr
Propagation	Two Ray	Two Ray	Two Ray
model	Ground	Ground	Ground
Radio frequency	2.47GHz	2.47GHz	2.47GHz
Channel bandwidth	2Mbps	2Mbps	2Mbps
Mac protocol Transmission	Mac/802_11	Mac/802_11	Mac/802_11
range of vehicles	250m	250m	250m
CBR data flow	5 Sessions	10 Sessions	15 Sessions

The map of the area in reference is shown in Fig. 3. On this map, traffic scenario in terms of number of vehicles, connections, turn, and flows is created. This traffic scenario is passed in MOVE [7] simulator to generate TCL script. The TCL script is imported in ns-2 simulator. The parameters used in final ns-2 simulation are listed in Table 2. In the simulation, for data flow model, CBR is used as network application and UDP (user datagram protocol) as source agent in vehicles. CBR packet size of 1000 bytes and bit rate of 64Kb per second is taken. This set of parameters help AOMDV to find and maintain the routes from source to destination.

• VII.    Experimental Setup and Result Analysis

We have implemented MO algorithm in C++. Further, the C++ code of MO is integrated with ns-2 using shell programming. It is important as the population generated by MO is passed in ns-2 for experimentation. This process is illustrated in Fig. 1. In the experiments, we have taken three VANET scenarios small, medium and large. These scenarios are defined according to the size of the map and number of vehicles running over. The small, medium and large maps contain 10, 20 and 30 vehicles, respectively

Table 3. Communication Costs

Map	Communication Cost
	Default	Optimized
Small Map	-0.053133	-0.1161
Medium Map	0.573276	0.08722
Large Map	0.841471	0.317861

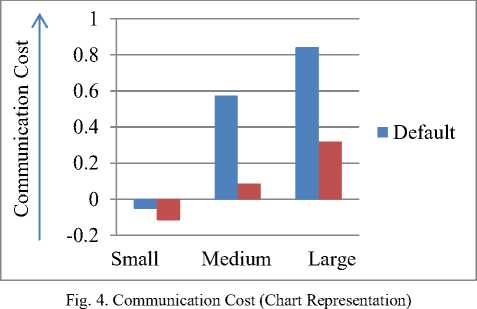
The experiment is conducted on 10 different simulation runs (10 different seed values) for the population size of 10, on each map size. As a result, we get an optimal value of parameters on each map size which is used to evaluate the communication cost. A significant amount of drop in communication cost is observed. The communication cost corresponding to default value of parameters and for optimized value of parameters is shown in Table 3 and Fig. 4 (chart representation) respectively. The default and obtained optimized value of parameters in all three scenarios are given in Table 4. The communication cost for small, medium and large map, has dropped by 118.51%, 84.79% and 62.23%, respectively. These drops in communication cost are very significant in the VANET. The relative change in each QoS metric for small, medium and large map is shown in Table 5, Table 6 and Table 7 respectively.

From Table 5, it can be seen that PDR for small and medium map have increased slightly, but for large map, there is little drop in it. In both the cases, the changes in PDR are not significant. Moreover, Table 6 shows significant drop in AE2ED for small, medium and large maps. Table 7 shows NRL for default and optimized set of parameters. NRL has dropped in all three small, medium and large scenarios. For checking the convergence of our modified algorithm for magnetic optimization, we have executed the algorithm 10 times over same set of randomly generated input parameters with different seed values for each map. The standard deviation of the 10 different Optimized communication costs generated for small, medium and large map came out as 14.68%, 12.29% and 4.58% respectively. The average of AE2ED for small, medium and large map size is 81.41% (drop). Similarly, average of NRL and PDR for small, medium and large map size is 39.24% (drop) and 0.77% (rise) respectively. The algorithm shows a drastic improvement in the performance of AOMDV using optimized value of parameters for the given scenario.

Table 5. PDR
Map	Default	NRL Optimized
Small Map	1.676156	1.514937
Medium Map	3.421847	1.492450
Large Map	4.478333	2.161913

Table 6. AE2ED

Map	AE2ED
	Default	Optimized
Small Map	0.099539	0.047664
Medium Map	0.307768	0.012751
Large Map	0.23968	0.008974
Table 7. NRL
Map	PDR Default	Optimized
Small Map	0.836452	0.866774
Medium Map	0.406848	0.430191
Large Map	0.252199	0.234428

Table 4. Optimized and default parameter values for small, medium, and large scenario

Parameters               A_R_T	A_H_L    M_R_T    N_T_T    R_R   T_S   T_I   T_T   N_D
Default                      3 Optimized for small map            10 Optimized for medium map           5 Optimized for large map            10	2            6           0.04         2        1        2        7        35 1               4               1            5          5         4         1          2 1               1             0.87          1          7         6         1          1 1                4               0.3            1           9          5          1           1
A_R_T=ACTIVE_ROUTE_TIMEOUT, M_R_T= MY_ROUTE_TIMEOUT, R_R= RREQ_RETRIES, T_I=TTL_INCREMENT,	A_H_L=ALLOWED_HELLO_LOSS, N_T_T=NODE_TRAVERSAL_TIME, T_S= TTL_START, T_T= TTL_THRESHOLD,

N D= NETWORK DIAMETER

• VIII.    Conclusion and Future Work

The performance of routing protocols in the given scenario critically depends on the parameters value used in the protocol. The number of parameters in AOMDV is nine and each parameter has a specified range of value which forms multiple combinations of the parameters value. All these combinations can be used but QoS of VANET may not be good on each combination. The nature of these combinations is of combinatorial optimization problem and it is impractical to test each combination in protocol to get an optimal set of combination. In this paper, therefore, an optimization technique (MO) is implemented and tested for AOMDV on real map scenario to obtain the optimal value of parameters which help in reducing the communication cost. The use of MO shows drastic improvement in QoS. There is 81.41% and 39.24% drop in AE2ED and NRL respectively, and 0.77% rise in PDR. There is a drastic improvement in the performance of AOMDV using an optimal value of parameters over the default value of parameters. Therefore, in future work, we will make an attempt to use the MO and other meta-heuristics to optimize different other protocols.