Optimized controller design using an adaptive Bacterial Foraging Algorithm for voltage control and reactive power management in Off-Grid Hybrid Power System

The far-off communities and small islands where it is difficult to have a connection from the central public utility, it is essential to have them energy solution which is cost efficient and environmentally friendly. Mix of different renewable energy sources called as hybrid power system is very promising solutions in such locations. Presence of large quantity of wind and solar energy observed in remote territories, makes possible to utilize them to fulfill their energy requirement. [1-2]. The concern with renewable sources is that they are undependable, to realize dependable and quality power supply requires suitable and efficient control techniques. The test system has power generation from Diesel, Wind, and PV System. The isolated power systems similar to test system have been already present in several small islands/ isolated communities [3].The IEEE type-1 excitation system is employed for SG coupled to Diesel engine and the IG is used for wind power generation. An IG needs reactive power for its excitation. The Reactive power required by the IG varies with slip (wind speed). The overall reactive power required by OGHPS varies with varying reactive power load demand and/or varying reactive demand of IG due to fluctuations in input wind power (mechanical power) to IG. Hence, for VAR management and voltage control, system reactive power is needed to be balanced by its sources and sinks under all operating conditions. Deficient reactive power in the system can cause severe drop in voltage; results in poor voltage profile stability. If voltage variation may go outside the tolerable limits, Condition of power supply will not be acceptable for consumers. Hence, it is obligatory to have a enough reactive power source to be present in the system. The earlier works reported in [4-8] for voltage and reactive power control of the wind diesel hybrid Power System are based on Static VAR Compensator (SVC) and Static synchronous compensator (STATCOM)] with load either static (exponential) or static plus dynamic. Some good works have been reported, but, the parameters of the SVC/STATCOM controllers were optimized while controller parameters of AVR of SG excitation loop were fixed, hence cannot assure the efficient co-operative control. The work in [9] proposed voltage control of wind diesel hybrid power system based on H∞ loop shaping control of SVC and AVR with static load only. In their work, SVC and AVR controller gains were optimally tuned at the same time and performed agreeably. However the gains of the SVC and AVR controllers were optimized for arbitrary load change with a fixed reactive power request by the IG, which isn't reasonable. The work in [10] investigated the application of the model predictive control of SVC and AVR for voltage profile stability of the islanded hybrid wind–diesel power system with static load model only and not considered dynamic load. A PV inverter can control the active and non-active power within the bounds obliged by its apparent power, is a fast acting, has superior transient performance, put off the need of a separate reactive power compensator, extra investment, hence is a convincing answer to address voltage regulation problem in OGHPS. PV inverter with surplus VAR capacity as a reactive power compensator for voltage control in OGHPS is proposed by author in previous work [11]. This work presents coordinate control of PV inverter and AVR to control voltage and reactive power of OGHPS considering detailed composite load model. Two control structure is incorporated in this work, the first control structure is for balancing reactive power of the system in the event of disturbances by inverter by controlling its voltage magnitude and the second control structure is for controlling the SG excitation by AVR to regulate the load bus terminal voltage. The both control structures have PI controllers with a single input. To incorporate realistic features in this study, the parameters of the PI controller in both control structures have been optimized at the same time With requirement of optimization of four parameters of both controllers simultaneously, under change of reactive load demand and /or change of reactive power need of IG due to wind input power change (wind speed), tuning strategies for PI controller of the system becomes very important. If PI controller parameters are not tuned effectively, may lead to oscillatory, sluggish control response and in the worst-case situation would result in collapse of system operation.

For PI tune, there are many conventional methods and some methods based on minimizing performance index criteria available in the literature, does not give acceptable result when the condition is to optimize several gains of the controllers under varying operating conditions [13-15].

In the recent years, optimal tuning of controller parameters using intelligent swarm based computing techniques such as the Bacterial Foraging Algorithm (BFA) has grabbed attention of researcher [16,17]. In the literature Bacterial Foraging algorithm has not been applied for reactive power control of inverter in OGHPS therefore BFA and its modified version combined with fuzzy logic, i.e. Fuzzy adaptive BFA is suggested in this work for tuning two controllers simultaneously. Optimal PI controller designing is mainly the outcome of minimizing a mathematical function (fitness function), which decides necessary control action.

In the view of the above discussion, this work focuses on VAR /voltage control of OFHPS considering the composite load model, with control parameters of the inverter and AVR tuned in coordination using BFA and GA when the system is subjected to varying disturbances.

The main contributions of this paper are: (i) development of optimal controller for inverter and AVR using original BFA and Fuzzy Adaptive BFA (ii) Time domain performance analysis of the system for step disturbances of differing magnitude and randomly varying load and wind power disturbances

• II.    Off-Grid Hybrid Power System Configurations

(OGHPS)

V< 0

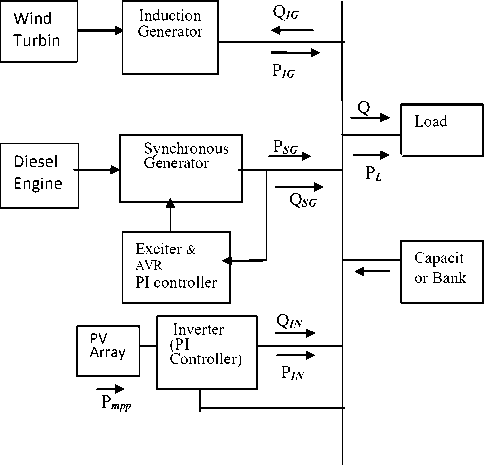
Fig.1. Test system- OGHPS schematic diagram .

The OGHPS considered for the study is illustrated in Fig.1, consist of SG (Diesel Engine) with a PI controller for its excitation control, IG (variable wind speed turbine), Single stage PV system interfaced with an inverter (PI controller for reactive power control) and a fixed capacitor bank(FC) to supply reactive power to IG at steady state are connected to a common load bus. Mathematical model of system components based on the reactive power balance equation, is implemented in Simulnik, to examine the voltage profile stability through VAR control under different disturbances. In this test system, power sources and load are assumed to close to each other.

• III.    Voltage - Reactive Power Equation With Composite Load Of The OGHPS

When the system is in a steady state condition, the system power balance equation will be governed by [4]

Qsg + Qin + Qcp = Ql + ^q ig          (1)

Under the varying operating condition such as change in reactive power load demand Q L and/or change in wind power input P _W , the system generates more reactive power is equal to AQ_in + AQ_sg , due to inverter and AVR of SG. The reactive power required for the system will also change due to change in voltage by ΔV. Then, the surplus reactive power in the system can be expressed as

^Q n = AQsg + AQin + AQcp-AQl - Mg  (2)

The 21Q_n , net surplus reactive power, which due increase in electromagnetic energy absorption ( Em ) of the induction generator by ^^and the increase in reactive load consumption, results in increase of the system voltage, can be expanded as [4,8,9]

^Qn = d?+ d^ ^s)

Where D_lvq is an increase in reactive power demand of all loads connected to the system due to voltage change. (D_lvq — reactive power change with voltage change).

In power system voltage stability is affected by choice of the load model and its parameter. Dynamic load models are essential for examining the effect of nonlinear loads in dynamic studies [18,19]. The Composite load provides a much more accurate representation of load response to the voltage [20]. Composite load represents the combined effect of aggregate of static and dynamic load (Induction motor) is shown in Fig.2.The participation ratio of static to dynamic load in composite load presentation for remotely located OGHPS is suggested as 4:1 in literature [21-23]. The OGHPS has a generation capacity of 400KW with load of 300KW. Total 300KW load has a static load (240KW) and dynamic load (60KW). An aggregate dynamic load model is developed considering group of seven Induction

Motors of ratings ranging from 4

KW to 20 KW

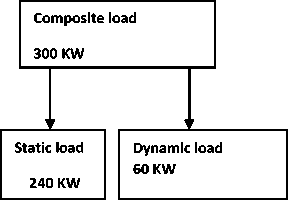
Fig.2. – Composite load structure

In order to take account the effect of the composite load Q_l in the system voltage- reactive power, given Eq.(2), load voltage characteristic D_lvq in Eq.(3) has two parts, one for static load D_lvq-st ,one for dynamic load D ivq-dy ,is governed by

^Dlvq = ^Dlvq-st ^{+ D}lvq-dy           ⁽⁴⁾

From [4, 19], we can write as

D lvq-st = q(Q Lst /V)             (5)

The expression for D_lvq-dy is developed based on the detailed fifth order model of induction motor [24] for 60 KW is obtained as

(0.98125 ^s + 1.301e4s ⁴ + 65e6S³ + 1.807e9S 2 + 2.037e11s + 7.9e12 )

• ^DlTQ-d = 5 ^s + 1.326e4s ⁴ + 3.817e65 ³ + 1.568e95 ² + 1.568e11s + 7.885e12)

Using Eq. (3), Eq. (4), Eq.(5) and Eq.(6), reactive power -voltage balance equation of OGHPS with the composite load model can be expanded as

A^Qsg ⁺ A^Qin + A^Qcp ^-A^Ql — A^Qig = ^(s){s(^)+ (D lvq-st + D l _V q-dy )}

To develop the simulation model of OGHPS, mathematical equation of other system components SG, IG and FC for incremental change in reactive power, exciter output voltage are available in articles [4-5,810,25] are used and incremental change in reactive power AQ_in of PV inverter is explained in authors previous work[11] is used in a Simulink model.

• IV.    PI Controller Parameter Optimization

For coordinate control, PI controller gain parameters ( Kp and Ki) of PV inverter and AVR, are to be optimized simultaneously. The two parameters of each controller formulate the optimization problem as four dimensional. The optimization task is to minimize the Objective function. The objective function considered for optimization problem is an Integral of Time multiplied squared Error (ITSE), is as given below.

Min (OB) = Min (ITSE) = Min [J" [t x AV(t)²]]  (7)

Subjected to:

Kp min ≤ Kp ≤ Kp max

Ki min   ≤ Ki ≤ Ki max            (8)

For PI controller parameter tuning, the conventional methods are based on performance index criterion such as IAE, ITAE, ISE and ITSE etc. The ITSE has more mathematical tractableness especially for higher order systems. In this work conventional method of PI tuning is based on ITSE is employed due to its advantage that it penalizes less to initial errors to support rapid settling of the controlled output [26]. Adaptive BFA method is applied in this work to solve for optimization problem described in Eq. (7) for the constraints in Eq. (8), The constraints in Eq. (8), are chosen from the earlier published work [11]. The optimal controller structure based on adaptive BFA is as shown below Fig.3,

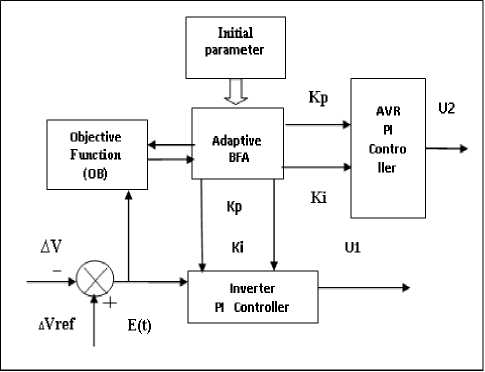
Fig.3.- Control structure for optimal tuning of PI Controllers based on Adaptive BFA

The control output from PI controller shown in Fig.3, is given by

U = K P AV + K I J AV dt          (9)

• A.    Overview Bactria foraging algorithm (BFA)

BFA is a social system based algorithm. It is a swarm intelligence method of optimization. BFA is based on foraging technique of E. Coli bacteria [27]. In this work BFA is proposed by [28], for optimization is called as original BFA (Basic BFA). Basic BFA have been applied successfully to engineering problems

Foraging property of bacteria is modeled as optimization process. From the view of optimization, in

BFA, optimal value is the place, having highest nutrient concentration [29]. The forging activity of bacteria is explained by chemotaxis, reproduction and elimination dispersal. BFA mimic forging principle to find optimal values of controller parameters. Optimization steps models how bacteria locate food is divided into chemotactic, reproduction and elimination-dispersal

Bacteria move towards the point of highest nutrient concentration by taking a random walk with fixed steps. This movement pattern of bacteria in the nutrient medium, is called as Chemotaxis. Once bacteria complete defined number of chemotactic steps, their health is checked and sorted depends on nutrient value they have obtained. Healthy bacteria equal to half of the population reproduce and remaining 50% of the population are unhealthy bacteria will die. Due to the external factors, some of the bacteria could disperse into other region of nutrient medium. This phenomenon causes bacteria to search most part or whole part of nutrient medium (search space).

The random walk of bacteria with fixed chemotactic step size in original BFA has two effects, a large value of step length aids bacteria to proceed to the optimum location speedily, but may fail to converge to the global optimum, on the other hand very small step size make certain that bacteria will find a global minimum point but need a large number of chemotactic steps to reach to the minimum point. Hence there is a need to improve basic BFA to accelerate the convergence and better global optimum value. Several variants of the BFA have been developed to improve its performance of optimization. [30,31], one of the ways to improve basic BFA is to make its step length adaptable during its run.

• B.    Adaptive Bacteria foraging algorithm

The large value of the fixed step size of the basic BFA results in oscillation near the optimum point, hence bacteria could not reach the optimum location, therefore the accuracy of the optimal solution decreases. In order to damp the oscillation, to obtain a best optimal solution, small step size is necessary close to minimum point.An approach to deal with this problem is to make bacterium moves with large step size at the early stage of the search process, and keep reducing the step size when the bacterium is close to the optimum location, increases bacterium's local search ability, to make certain that bacterium will reach the optimum point. Thus, it is required to make chemotactic step size adaptive. The chemotactic step size can be altered according to the objective value; if the objective value is high means bacterium is far away from the global optimum point, then large step size and if the objective value is low, the bacterium is near to optimum point then the step size is small. In this work chemotactic step size is made adaptable on the basis objective value (nutrient value) of every bacterium using Fuzzy Logic, hence called Fuzzy adaptable BFA (FABFA), In this approach step size of each bacterium is decided by fuzzy logic method on the basis of its objective value. The fuzzy model is developed with one linguistic input variable and one output linguistic variable.

Input to Fuzzy model is objective function value (ITSE) of every bacterium and the output is desired step-size (Sfa) for every bacterium to walk in the search space, is as shown in Fig4.

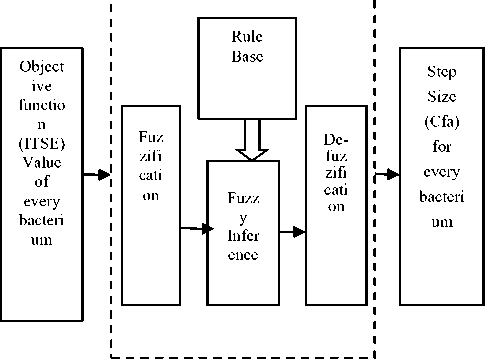
Fig.4.- Fuzzy logic structure for adaptive step size

The procedure to design Fuzzy logic structure for adaptive step size is as.3

• 1.    Definition of input and output parameter - The input variable is the objective function value (ITSE) of every bacterium and output variables desired stepsize (sfa- fuzzy adaptable step size) to be applied to every bacterium to walk in the search space,

• 2.    Definition of parameters in fuzzy sets - Input and output variable have been categorized into seven sets of linguistic variables: VVlow, Vlow, Low, Med, High, Vhigh, and VVhigh. Gaussian membership function (MF) is selected for fuzzy input and output because the Gaussian curve has the advantage of smooth and nonzero output on all points. The center and width parameters of Gaussian curve are selected by trial and error. The input space for Gaussian membership functions are selected suitably to cover a range of input and output.

• 3.    Building of control rules- The linguistic rules statement is the heart of Fuzzy model. For adaptable step size, the requirement is to have large step size when the objective function value is large and very small step size when objective function value is very small. Input to output variables in this fuzzy logic structure has one to one relation, Hence seven fuzzy rules are defined as,

• R1: If the Objective function is VVhigh, then step size is VVhigh

• R2: If the Objective function is Vhigh, then step size is Vhigh

• R3: If the Objective function is High, then step size is High

• R4: If the Objective function is Med, then step size is Med

• R5: If the Objective function is Low, then step size is Low

• R6: If the Objective function is Vlow, then step size is Vlow

• R7: If the Objective function is VVlow, then step size is VVlow

• 4. Defuzzification method - The Centroid of the area is used in this work

By applying the above steps, a subroutine code is written MATLAB, for fuzzy memberships and rules to develop fuzzy model and then called this code into the main code of BFA.

The computation steps of FABFA to solve the optimization problem to find optimal solution is explained as

Step 1. Initialize the BFA parameters, (Number of bacteria ( N), Number of chemotactic steps (N_c ), Limit of a swim (N), Number of reproduction steps ( N_r ), Number of elimination-dispersal events ( N_ed ), the probability that each bacteria will be eliminated/dispersed ( P _Ed)

Step 2. Elimination-dispersal loop counter for EL=1 to N ED , do EL=EL+1

Step 3. Reproduction loop counter for R =1 to N _R ,do R=R +1

Step 4. Chemotactic loop counter for C =1 to N _C ,do C=C +1

For I = 1 to N,

• a.    Compute the objective function, OB ( I, J, R, EL ) for every bacterium, save as OBlast = OB ( I, C, R, EL ), to compare this value with other best values which may found during a run of the algorithm.

• b.    Tumble- Generate a random vector i(I) £  ^^z ,

in the z (z=4) dimensional search space for each element A E (I) , E= 1, 2, 3,4 and a random number [-1,1] and compute the movement of bacterium I from position P ( I, C, R, EL ) to position P ( I, C +1 , K, EL ) =

P ⁽ RE)+^Sf«d ₍ I ^^p^)  (10)

This represents a movement of bacterium with step length of sfad in the direction of the tumble. The step size ‘Sfad’ value is obtained from the Fuzzy model.

• c.    Compute OB (I C +1 R EL ) for every bacterium for new position P ( I C +1 R EL ),

• d.    Initialize swim loop counter m= 0

• • While m< N _s , do m = m +1; if OB( I, C+1,R,EL ) < OBlast( bacterium moving in right the direction) then Oblast = OB( I,C+1,R, EL ) and calculate position of bacterium as

  P( I,C +1 ,R,EL ) =P( I,C +1 ,R,

  
  

EL )+Sfad ( I )( . /^(/)   )

VaWaO)

• Else, m= N_s (End of loop)

• e.   If I ≠ N to step 4b for next bacterium (I=I+1)

Step 5. If J < N C , go to step 4

Step 6. Reproduction

• •    Calculate the health of the bacterium I, OB heaith = t^OBU.C.R.EL) and sort

Values of bacteria in ascending order (In this work, higher objective function value (ITSE) indicates unhealthy bacteria)

• •    The bacteria with the higher   OB h _ealt h value

will die and other healthy bacteria go through the process of split up to the maintain population

Step 7. If R < N R then go to step (2),

Step 8. Elimination-dispersal For I = 1 to N, bacterium which has probability value less than P_ED get eliminated and dispersed to a random position in the search space

Step 9. If EL < N ED , go to step 2, else end

FABFA based on the above steps is implemented in MATLAB. Fuzzy input and output MF are illustrated in Fig.5 and Fig.6 respectively. The fuzzy surface obtained for a fuzzy model developed for adaptive step size, which maps, objective function with step size is shown in Fig, 7

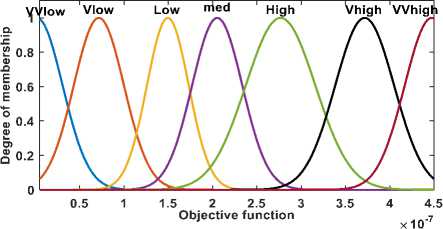
Fig.5.- MF for Input (Objective Function)

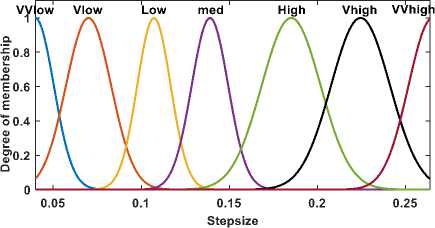
Fig.6- MF for output (step size)

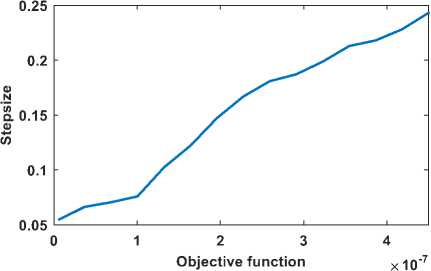
Fig.7- Fuzzy surface (Objective Function- step size)

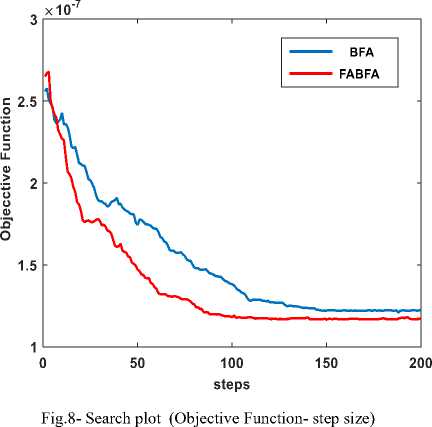
The search plot for basic BFA and FABFA is illustrated in Fig.8. It is clear from the graph that converge speed (number of chemotactic steps) and the optimal value of the objective function is improved for FABFA compared to original BFA. The convergence steps required finding the optimal point for FABFA is 107 and convergence steps for BFA is 164.

For FABFA and BFA, parameters are selected so that bacteria will have adequate chemotactic steps in the direction of global optimal location, sufficient number of the reproduction process and elimination –dispersal occurrence so that bacteria can search entire search space. For FABFA and BFA life time of bacteria is determined by N_cxN_Kx M_ED . For the basic BFA, step size value is selected as 0.15, while for FABFA step size range is [0.05 0.25].

• V.    Simulation Results And Discussion

Case 1 - Transient performance of the system for Step disturbance of 5% of reactive load demand Q L

Time(sec)

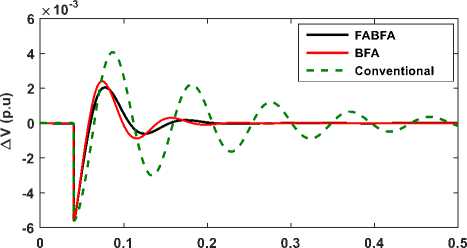
Fig.9 – Transient response of ΔV.

Time(sec)

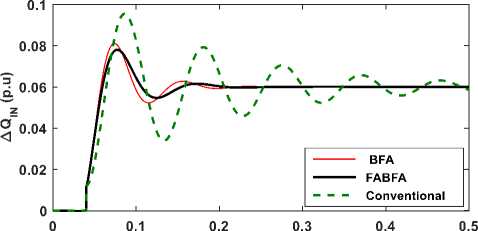
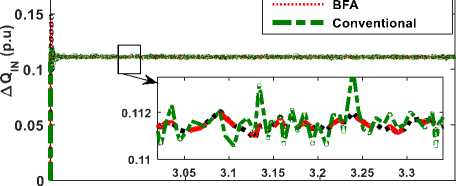
Fig.10 Transient response of ΔQ IN

Time(sec)

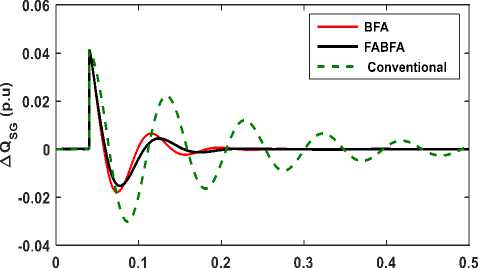
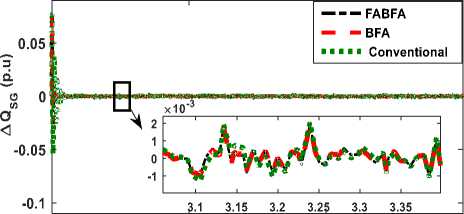
Fig.11- Transient response of ΔQ SG

Time(sec)

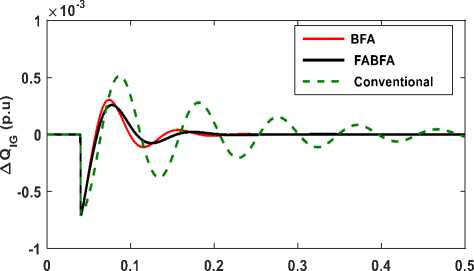
Fig.12- Time response of ΔQ IG

The time domain responses of deviation in system state variable such as voltage, inverter reactive power, synchronous generator reactive power and induction generator for a step increase of 0.05 p.u. (5%), in reactive loading at t= 0.04 Sec, at the constant wind power input to IG are illustrated in Fig. 9 to Fig12. The System is in steady state till=0.04 Sec, prior to change in reactive load demand. From the Fig.9 to Fig.12, it is observed that inverter provides dynamic support of reactive power to mitigate the load disturbance, while the AVR of synchronous generator initially support by taking action to maintain the voltage level following the disturbance. From the responses shown in Fig. 9 to Fig12, it is evident that control characteristics such as Peak value, Oscillation and settling of state variables are improved considerably in case of FABFA, BFA based Optimal PI controllers compared to conventional tuned PI.

Case 2 – Transient performance of the system for 10% Step disturbances in reactive load demand as well as wind power

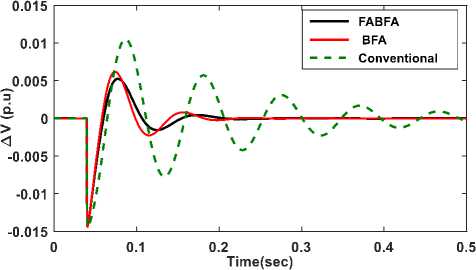
Fig.13 –Transient response of ΔV.

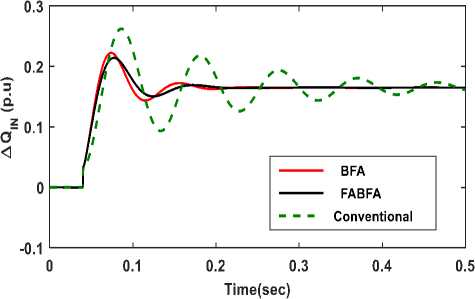
Fig.14- Transient response of ΔQ IN

Time(sec)

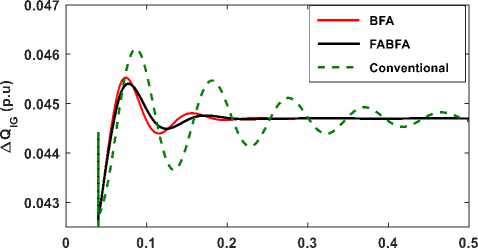
Fig.16- Transient response of ΔQ IG

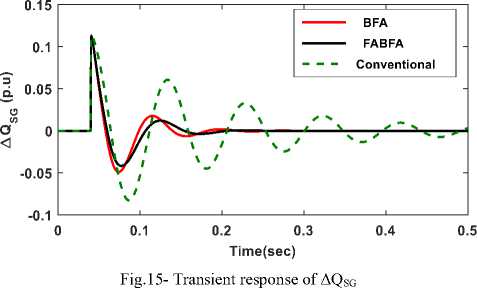
The time domain response of deviation in system state variable such as voltage and reactive power of the inverter, SG and IG for the step increase of 0.1 p.u. (10%) in both reactive power loading and wind power input to IG at t=0.04 Sec, is illustrated in Fig.13 to Fig. 16. In this case mechanical wind power input to IG changes, slip of IG changes, and hence reactive power demand of IG changes. The net increase in the reactive power of demand is ∆ Q IG + ∆ Q L . Due to the action of Inverter and AVR, the reactive power generated by the inverter and SG varies according to the increase demand, to balance system reactive power and hence to suppress the voltage deviation of the system voltage. From Fig.13 to Fig. 16., it is observed that the system parameters regain steady state condition quickly with a FABFA and BFA control compared to Conventional control method. The response of the state variables ∆V and ∆Q SG , becomes zero are as shown in Fig.13 and Fig.15. The Peak value and Oscillation of state variables are reduced considerably in the case of FABFA, BFA compared to Conventional.

Case 3- Transient performance of the system for random disturbance in reactive load demand as well as wind power input to IG.

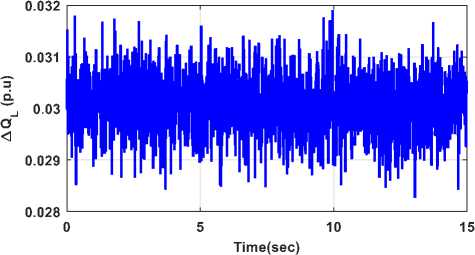
Fig. 17 – Random disturbance in reactive power load demand

0.0702

0.0701

5 0.07

0.0699

0.0698

0                               5       -г-     , x 10

Time(sec)

Fig. 18 – Random disturbance in wind power input to IG.

FA В FA

----- В FA

■ ■ ■ Conventional

Time(sec)

Fig. 19 – Transient response of ΔV

0.2

FABFA

5           , x 10

Time(sec)

Fig. 20– Transient response of ΔQ IN

О                  5 Time(sec) 10                 15

Fig. 21 – Transient response of ΔQ SG

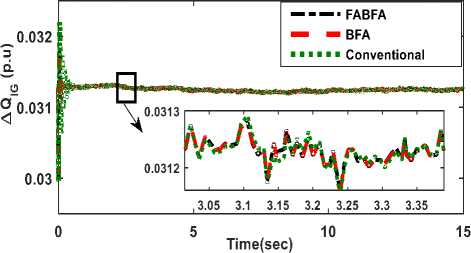
Fig. 22 – Transient response of ΔQ IG

In OFHPS system, the load is mainly residential and commercial type. The behavior load is fluctuating and random. Wind power generated by wind generation system is an intermittent in nature due to fluctuating wind speed. Hence the of random variation in load and wind power is considered in this case is as shown in Fig. 17 and Fig.18. The test system is investigated for random variation in load and wind power. The transient responses of a system state variable (voltage, reactive power of the inverter and reactive power SG) for random variation in reactive loading and wind power are illustrated in Fig.19 to Fig. 22.

The random variation of load and wind power results in voltage deviation, which is suppressed by the action of inverter and AVR, by generating required reactive power to balance system reactive power. It is clear from Fig.19 to Fig. 22,that coordinately optimized PI controllers by FABFA and BFA exhibited better dynamic reactive power control outcome hence improved stability of voltage, compared to the conventionally tuned the PI controller under random disturbance condition.

The optimal values of controller parameters obtained by FABFA and Basic BFA for the case 2, are given in the Table 1.

Table 1. Inverter and avr controller parameters obtained by FABFA and BFA (case 2)

		Inverter		AVR
Optimi zation Method	Minimum value of Objective function	Kp	Ki	Kp	Ki
FABF A	0.1166E-6	21.417	2235.1 7	26.3 27	17.996
BFA	0.1219E-07	21.087	2842.9 92	44.2 24	50.4913

In order to assess the effectiveness of optimization method FABFA and BFA for optimal control, the voltage deviation in p.u for 5% reactive loading(case1) and 10% reactive loading and 10% wind power change (Case 2) is presented in Table 2. The inverter and AVR coordinated control performance for FABFA, BFA and conventional method in terms of settling time is presented in Fig. 23.

Table 2. Voltage deviation for different disturbance condition

Disturbance condition	FABFA	BFA	Conventional Method
Case 1	.002	0.0024	0.00395
Case 2	0.0065	0.00567	0.01070

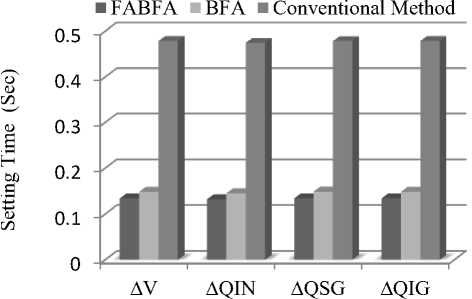
Fig.23 – Comparison of the dynamic performance of controllers in terms of the settling time for the case 2. (10% disturbance condition)

From the numeric data given in Table 2 and Fig. 23, it is observed that the maximum deviation with respect to a steady state value and settling time is reduced for FABFA compared to BFA based optimal PI controllers.

• VI.    Conclusion

Voltage /VAR control of OFHPS considering a composite load model with optimally designed controllers, for the inverter and AVR is studied in this work. In order to have coordinated control inverter and AVR controller parameters are optimized simultaneously. The system model based on reactive power – voltage characteristics is simulated in Simulnik, is tested for designed optimal controllers under changing operating conditions to investigate the voltage profile stability. Simulation is carried out for step disturbance of different magnitude and randomly varying disturbance of reactive load demand and wind power to study the dynamic performance of the system.

Comparative performance of FABFA optimized controllers with BFA optimized controllers exhibited that the response of FABFA optimized controllers is enhanced in terms of peak deviation and settling time for all system state variables.

From this work, it can be concluded that FABFA, BFA optimal tuned PI controller of inverter and AVR controllers have a better control effect, but the overall performance FABFA tuned PI controllers outperformed the BFA tuned PI controllers. FABFA controlled OGHPS worked robust even under arbitrary varying disturbance condition.