Optimized Solution of Two Bar Truss Design Using Intuitionistic Fuzzy Optimization Technique

Published Online August 2014 in MECS

The structural optimization is an important research topic in structural and civil engineering. Structural optimization problems consist of determining the configurations of structures which obey assigned constrains and produce an extremum for a chosen objective function. In the reality structural engineering design problems, the input data and parameters are often fuzzy/imprecise with nonlinear characteristics that necessitated the developments of fuzzy optimum structural design method. Fuzzy set (FS) theory has long been introduced to handle inexact and imprecise data by Zadeh [1]. Later on Bellman and Zadeh [2] used the fuzzy set theory to the decision making problem. Intuitionistic fuzzy set (IFS), is one of the generalizations of fuzzy set theory, is characterized by a membership function, a non membership function, and a hesitancy function. Intuitionistic fuzzy optimization (IFO) is very suitable for the depiction of the uncertainty and vagueness of things. IFS was first introduced by Atanassov [3,8 and 10] and has been found to be well suited for dealing with problems concerning vagueness. The concept of IFS can be viewed as an alternative approach to define a fuzzy set in a situation where available information is not sufficient for the definition of an imprecise concept by means of a conventional fuzzy set. In fuzzy sets the degree of acceptance is only considered but IFS is characterized by a membership function and a non-membership function so that the sum of both values is less than one [16].

Some researchers have used the technique of fuzzy set theory for solving structural model. Structural optimization with fuzzy parameters was developed by Yeh and Hsu [6]. In 1989, Xu [5] used two-phase method for fuzzy optimization of structures. In 2004, Shih and Lee [14] used level-cut approach of the first and second kind for structural design optimization problems with fuzzy resources .Shih, Chi and Hsiao [12] develop an alternative α -level-cuts methods for optimum structural design with fuzzy resources in 2003. Dey and Roy [18] optimize structural model in fuzzy environment. Nasseri and Alizadeh [20] use fuzzy geometric programming technique to optimize solution of a two bar truss. Dhar and Baruah[19] described some new definitions for some of the terms often used in the theory of fuzzy sets . But very rarely literatures reported engineering designs and applications with intutionistic fuzziness existing in the real-world problems.

Now intuitionistic fuzzy optimization (IFO) is an open field for research work. Very little research work has been carried out on IFO. Angelov [9] implemented the optimization in an intuitionistic fuzzy environment. Angelov [7] also contributed in another important paper, based on intuitionistic fuzzy optimization. Wei [17] used the maximizing deviation methods to solve the intuitionistic fuzzy multiple attribute decision making problems with incomplete weight information. Pramanik and Roy [13] solved a vector optimization problem using an intuitionistic fuzzy goal programming. A transportation model was solved by Jana and Roy [15] using multiobjective intuitionistic fuzzy linear programming.

In this paper, a well known two bar truss [11] design model is considered as a Structural design model. The results are compared numerically both in fuzzy optimization technique and intuitionistic fuzzy optimization technique. From our numerical result, it is clear that intuitionistic fuzzy optimization provides better results than fuzzy optimization.

The advantage of the intuitionistic fuzzy optimization technique is twofold: they give the richest apparatus for formulation of optimization problems and on the other hand, the solutions of intuitionistic fuzzy optimizations can satisfy the objective(s) with bigger degree than the analogous fuzzy optimization problem and the crisp one. This paper envisages the application of IFO in context of structural design.

The remainder of this paper is organized in the following way. In section II, we discuss about structural optimization model of a two-bar truss. In section III, we discuss about intuitionistic fuzzy set, ( а , в ) -level intervals or ( а , в ) -cuts. In section IV, we discuss about Intuitionistic fuzzy approach for solving nonlinear programming problem with linear membership and nonmembership functions. In section V, we discuss about Intuitionistic fuzzy optimization technique on structural optimization Problem. In section VI, we discuss about numerical solution of structural model of two bar truss and compared results by Intuitionistic Fuzzy Non-linear programming (IFNLP) technique and by fuzzy non-linear programming (FNLP) technique. Finally the conclusions were drawn in section VII.

л/x B + ^{( l} + ^y B ⁾²

subject to C T ( A_b A 2 , у в ) - —-------------- lA ₁

4 ^c t 1 ;

c c ( 4, a 2 , у в ) - P + y^{B 2}  C 1 ;

lA ₂

A ! >  0; A ₂ >  0;

where weight = WT ,nodal load = P , volume density = p , length AC = l ,perpendicular distance from AC to point B= xB , allowable tensile stress = [ct ] ,allowable compressive stress = [cc ] ,cross sectional area of AB bar = A1 ,cross-sectional area of BC bar = A2 ,y coordinate of node B = yB .

Sometimes slight change of stress of the structure enhances weight of the structure. Such a situation, when decision maker (DM) has doubt to decide the stress constraint goal, may induce the idea of acceptance boundary and negative response margin of constraints goal. This fact seems to take the constraint goal as an intuitionistic fuzzy set instead of fuzzy set, which will be more realistic description than others. When stress constraint goal is intuitionistic fuzzy in nature of the above non-linear structural optimization programming problem becomes intuitionistic fuzzy non-linear structural optimization programming (IFNLSOP) problem with intuitionistic fuzzy resources, which can be described as follows:

Minimize WT ( A_vA 2 , y B ) = p

^A 1 V ^x B + ^{( l} + ^y B ) 2

• II.    Optimization Model of a Two Bar Truss

  Optimization Model of a Two-Bar Truss shown in Figure 1 is designed to support the loading condition. The truss is subject to constraints in geometry, area, stress [11].

  
  

  subject to C t ( A ! , A 2 , y B ) -

  
  

  Pl^x B + ^{( l} + ^y B ) 2

  
  

  lA ₁

  
  
  
  
  
  

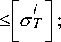
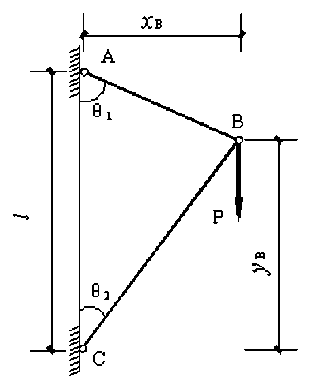
  Fig. 1. Design of the two-bar planar truss

  
  

  ^C C ^{( A} 1 , ^A 2 , ^y B ) ^-

  
  

  ^xB + y B²

  lA ₂

  
  
  
  
  

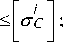
  A 1 >  0; A ₂ >  0;

  
  

  Here the constraints goals are characterized by intuitionistic                   fuzzy                   set

  O" T = ( c t ^{( A} 1 , A 2 , ^y B ), p i ^{( A} 1 , A 2 , ^y B^{) u} i ^{( A} 1 , A 2 , ^y B )) ^where

  CT

  p i ( A 1 , A ₂, y_B )   , u i ( A 1 , A ₂, y_B )   are the degree of

  CT

  membership function and the degree of non-membership function of IFS c T and C c = ( c _C ( A 1 , A ₂, y_B ), p , ( A 1 , A ₂, y_B ), C C

  U i (A, A,yB) where P i (A1, A2,yB) , и i (A, A2,yB) are the CC                        Cc

  degree of membership function and the degree of nonmembership function of IFS C _c .

  
  

The structural model can be written as

• III.    Prerequisite Mathematics

  Minimize WT ( A_vA 2 , у в ) = p

  
  

  ^A 17 ^x B + ^{( l} + ^у в ) 2

  
  

  A. Intuitionistic Fuzzy Set

  
  

  _v + A 2 7 x B + y B

  
  
  
  

  Let a set X, an Intuitionistic fuzzy set (IFS) A ⁱ in the sense of Atanassov is given by equation

  
  

A = {^x, цt (x), иi (x)^ / x g X}   where the function ц i (x): X ^ [0,1] and и t (x): X ^ [0,1] with the

A                         A condition 0 < ц t (x) + и t (x) < 1, Vx g X The numbers, AA ц i (x) g[0,1] and и t (x) g[0,1] denote the degree of AA membership and the degree of non-membership of the element x to the set Ai , respectively. For each IFS Ai in X, the amount n i (x) = 1 - (ц i (x) + и i (x)) is called the

A   AA degree of indeterminacy (hesitation part), which may cater to membership value, non-membership value or both.

B. ( a , ft ) -level interval or ( a , в ) -cut

A set of ( a , в ) - cut ,generated by an IFS A where а , в g [ 0,1 ] are fixed numbers such that a + в <  1 is defined as

A a , в =1 ( x , ц _i ( x ), u _i ( x )): x g X , ц _i ( x ) >  a , u _i ( x ) <  в , а , в g [ 0,1 ] к AA A A

We define ( a , в ) - level or ( a , в ) - cut, denoted by A a , в , as the crisp set of elements x which belong to a ⁱ at least to the degree a and which belong to A at most to the degree в .

• IV.    Mathematical Analysis

• A. Intuitionistic Fuzzy Non-Linear Programming (IFNLP) technique to solve Single objective Nonlinear Programming Problem

A non-linear programming problem (NLP) may be taken in the following form:

Minimize f ( x )

subject to gj(x) 0,

In general constraints goals are considered as fixed quantity. But in real life problem, the constraint goal cannot be always fixed. So we can consider the constraint goal for less than type constraints at least b _j and it may possible be extended to b j + b 0 . This fact seems to take the constraint goal as an intuitionistic fuzzy set and which will be more realistic description than others. Then the NLP becomes IFNLP problem with intuitionistic fuzzy recourses, which can be described as follows:

Minimize f ( x )

subject to gj(x) 0,

To solve the IFNLP (4) problem, following Werner [4] and Angelov [7], we have presented a solution procedure to solve the IFNLP problem by IFO technique ,and the following steps are used:

Step 1: Following Werner’s approach solve the objective non-linear programming problem without tolerance in constraints (i.e. g _y( x ) <  b .), with tolerance of acceptance in constraints (i.e. g _y ( x ) <  b . + b ⁰ ) by appropriate nonlinear programming technique.

Here they are

Sub-problem-1

Minimize f (x) subject to gj(x) < bj , x > 0 , j = 1,2,...,m

Sub-problem-2

Minimize f ( x ) subject to g j^{( x} ) <  b j + ^b”, x >  0 , j = 1,2,..., m

We     may     get     optimal x * = x1, f (x *) = f (x1) and x * = x2, f (x*) = f (x2)

solutions

Step 2: From the result of Step 1, now we find lower bound (minimum) L ^acc and upper bound (maximum) U^a<:< c by using following rule    U^acc = max { f ( x ¹), f ( x ²) } ,

Z^acc = min { f ( x ¹), f ( x ²) } .But in IFO the degree of nonmembership (rejection) and the degree of membership (acceptance) are considered so that the sum of both values is less than one. To define the non-membership function of NLP problem, let U ^rej and L ^rej be the upper bound and lower bound of the objective function f ( x ) where L^acc <  E^ej <  U^rej <  U^acc . For objective function of minimization problem, the upper bound for nonmembership function (rejection) is always equals to that the upper bound of membership function (acceptance). One can take lower bound for the non-membership function as follows L e = L^acc + 8 , where 0 <  s <  ( v a'c - L^acc ) , based on the decision maker choice.

Step 3: Here for simplicity linear membership function ц<х )( f ( x ) ) and linear non-membership ц,^ Д f ( x ) ) for the objective function f ( x ) is defined as follows:

1           iff (x) < Lacc ц     (f (x)) = j Uacc - f (x)

Цf (xЛ^ ’ I Uacc - Lacc if Lac < f (x)< Uac

iff ( x ) > U^acc

	0	if f ( x ) < Lrej
u , ( x )(. f ( x ) ) = •	f ( x ) - Lrej Urej - Lrej	ifLrej <  f ( x ) < Urej
	. 1	if f ( x ) > Urej

With tolerance ( U ac - L ac ) for the degree of acceptance and ( U re - L e ) for the degree of rejection of objective function f ( x ) .

and linear membership function " ^ Д g. ( x ) ) and linear non-membership u_g^ Д g ( x )) for the constraint function g ( x ) is defined as follows:

	1                  ifg. ( x ) <  bJ
"g^ x ) ( gJ(x ) )='	f b . + b 0 )- g .( x ) ^.ЦJ— ifb. <  g .( x ) <  b. + b 0 0      jj  jj J
	o                  if gj ( x ) >  bj + b *0

0            fg.(x)< bj + e и        g .(x)) = • gj ( )  ( j----j- ifb. + e. < g .(x)< b. + b 0

g (xГ/          ь0 _ e.        j j j-1  ’ j j j                     j J

1                ifgj( x)>     bj where 0 < ej < b0 . Rough sketches of the membership function and non-membership function for objective function and constraints function are shown in Fig.2 and Fig. 3 respectively.

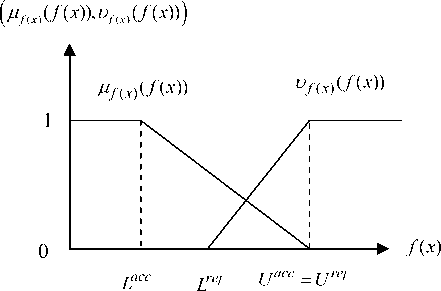
Fig. 2. Rough sketch of membership and non-membership function for objective function

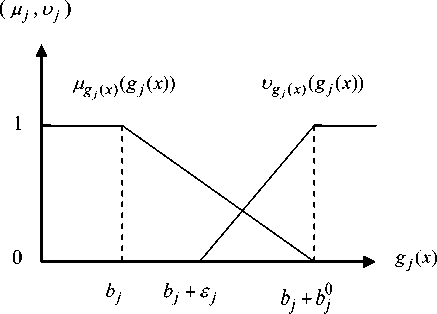
Fig. 3. Rough sketch of membership and non-membership function for constraints functions

Step 4: Now an intuitionistic fuzzy optimization for above problem with membership and non-membership function can be written as

	f                                 x)
Maximize	" f ( x ) ( f ( x X^ g ,( x ) ( gj ( x ) ) ■
	,                                   '             (7)
Minimize	_ U f ( x ) ( f ( x »^^g, ( x ) ( gj ( x > )/
subject to

" f ( x ) ^{( f ( x ) ) +} ”f ( x ) ^{( f ( x} > ) < ^1;

■( x ) ( gjx * ' " gj ( x ) ( Jx ⁾ )< ^1; " f ( x ) ^{( f ( x} »> ^u f ( x ) ^{( f ( x ) ) ;} " . x ) ( gj ^{( x )} )> " g/ x ) ( ^gJ ^{( x )} ) " f ( x ) ^{( f ( x}» , " g_f ( x ) ( ^gj ^{( x )} )> 0;

x >  0; j = 1,2,......, m

According to Angelov 9] to the above can be written as

Maximize ( a - P )

subject to

"f ( x)(f(x))2 “•  uf (x/■f(x ))< в

"g, (x )(gj(x ))г “•  "E)(x )(gj(x ))< в a + в < 1, a e [0,1], в g[0,1];

which on substitution for " f . _x ) ( f ( x )) , u f . _x ) ( f ( x )) , " g, ( x ) ( g j ( x )) and u _gj ( x ) ( g j( x )) for j=1,2,_,m. (8) becomes

Maximize ( a - в )

subject to f ( x ) + a ( Uac^c - L^acc ) <  Uac^c f ( x ) - в ( U^ree - L^rej ) < L^acc gj ⁽ x ^{) + a b}j ⁰ < bj ⁺ bo g j ⁽ x ^{) - в (} b00 ^{- e} j ⁾ < ⁽ bj ^{+ e} j ⁾ a + в <  1, a e [0,1], в e [0,1];

Step 5: Solve the above crisp model by an appropriate mathematical programming algorithm to get optimal solution of objective function.

To solve the non-linear structural optimization programming problem (2), step 1 of 4.1 is used. After that according to step 2, the bounds of objective are WT ^acc , WT ^acc   for weight function    WT ( A , A , y )

(where       W acc <  WT ( A , A , y_B ) <  W^ c      )      and

WT re ,WT Ue (where W re <  WT ( A 1 ,A 2 ,y_в ) <  W Ue ,) where W = W re ; W re = W + e such that 0 <  e <  ( W A - W acc ) are identified.

Here for simplicity linear membership function

( WT ( A , A , y_B ) ) = ^ ( WT ) and linear nonmembership и ( WT ( A , A , y_B ) ) = o_w ( WT ) for the objective function WT ( A , A , y_B ) is defined as follows

According to IFO technique, having elicited the above membership and non-membership function for NLP (2) crisp nonlinear programming problem is formulated as follows

	1	if WT <  Wracc L
	Wacc	- WT
^ WT ( WT ) = '	U acc	----- if wacc <  WT <  wacc acc     L          U WL
	U
	0	i f WT >  wacc U

0        if WT <  Wre

Maximize ( a - B )

subject to

^ WT ⁽ WT ) > ^a ’   ^UWT ⁽ WT ) < ^e ;

— ^{( -}T ) > ^a ’   ^Ua_T^-T ) < ^в ;

^-_c ^{( -}C ) > ^a ’    ^u -_c ^{( -}C ) < ^e ;

a + p <  1’ a e [0’1]’ P e [0>1];

which on substitution for ^ ( WT ) ’   ц. ( WT ) ’

ц „_т ( ^- t ) ’ ^u „_t ( ^- t ) ’ B _Oc ( ^- c ) and u „_c ( ^- c ) (10) becomes

Maximize ( a - в )

subject to

WT - WUe

T ( ^WT ) = ] rej A if WL <  WT <  WU

WT       Wre - W^Ue    ^{L        U}

1         if wt >  wUe

I                 U and       linear       membership       function рат (— (A, A, Ув)) = ВОт (—r) and linear non-membership V— (—t (A1’ A2, Ув )) = V— (—,) for the constraint function —r (A, A,Ув) is defined as follows:

p ( A 1V xB + ( l + Ув )² + A 2 V xB + УB ) + a ( WUcc - WLacc ) <  WUcc

P ( A 1V xB + ( l + УB )2 + A 2\/ xB + УB )" в ( ^W Ue - WUe ) <  ^W Le

pjx 2 + ( l + У в )²     I

—---+ a—

lA

¹ p <  —p + —p

PpB+BBfyB)2 А 0 А lA         в (-t - e1)< -t + e1

P^B + ^Ув + a— 0

lA           ^C

< ^— c ^{+ —} C

if ^—T ⁽ A , A 2, ^Ув ) <  ^—T

— ^{( —}T ) =

(^—T + ^—T )   ^—T ⁽ Ai , A 2, ^ув )

— T

if ^— p <  ^—p ( ay , A 2 ’ ^Уg ) <  ^—p ^{+ —}p

if ^—T ⁽ A 1’ A 2’ ^УB ) > ^—T

if ^— t ( A1’ A 2’ ^У в ) <  ^— T ^{+ e} 1

— ^{( —} t ) =

and

^— T ( A 1’ A 2’ yB ) ^{( —} T ^{+ e} 1)

'T - e 1

if — + e <  — ( a , A , Ув ) < — + — ⁰

linear

if ^—p ⁽ A ) >  ^—p ^{+ —}p

membership

function

Я, ( — ( A i, A , Ув ) ) = ^ _c ( — с) and linear non-membership и ( — ( A , A , y_B ) ) = и ( — ) for the constraint function — _c ( A , A , Ув ) is defined as follows:

¹                         if ^- _c ⁽ A 1, A 2, ^Ув ) <  ^- _c

— ^{( -} c ) =

^{( —} C ^{+ —} C ) - ^— C ⁽ A 1’ A 2’ ^УB )

^{if —} C <  ^— C ⁽ A 1’ A 2’ ^УB ) < ^— C ^{+ —} C

if ^— C ⁽ A 1’ A 2’ ^УB ) > ^— C ^{+ —} C

i^{f -} c ⁽ A1’ A 2’ ^Ув ) < ^- c ^{+ e}- 2

^U-c ^(- c ) =

^- C ( A 1’ A 2’ ^УВ ) - ^{( -} C ^{+ e} 2) 0

^- C   ^e - 2

i^{f -} C ^{+ e} 1 <  ^- C ( A 1’ A 2’ ^УВ ) < ^- C ^{+ -} C

i^{f -} c ⁽ A 1’ A 2’ ^Ув ) > ^- C ^{+ -} C

4^xB ⁺ Ув² lA

- ^в ( ^— C - ^e 2 ) < ^— C ^{+ e} 2

a + в <  1. a e [0,1], в e [0.1] A >  0’ A ₂ >  0.

Solve the above crisp model (11) by an appropriate mathematical programming algorithm to get optimal solution of objective function i.e. structural weight.

The input data for the NLP (2) is given as follows:

Nodal load (P) =100KN; Volume density ( p ) = 7.7 KN / m ³ ; Length ( l ) =2000 mm ;Width ( x_B ) =1000 mm ; Allowable tensile stress [ — t ]=130 MPa with a fuzzy region of 20MPa;Allowable compressive stress [ — _c ] = 90 MPa with a fuzzy region of 10 MPa ;

Solution: According to step 2, Here W U ^acc = 14.23932 = W Ue ’ W_L ^acc = 12.57667 ’ W fe = W acc + e . Here linear membership and nonmembership function for the objective function WT ( A ₁, A ₂, y_B ) is defined as follows:

1              ifWT <  12.57667

^ WT^(WT ) ='

14.23932 - WT

1.66265

if 12.57667 <  WT <  14.23932

0             ifWT >  14.23932

if WT < 12.57667 + e

^if a C ^{( A}_vA 2> yB ) <  ⁹⁰

^ WT^(WT ) =

WT ^(12.57667 + ^e ) if 12.57667 + e < wt < 14.23932 1.66265 - e                   ¹

1                     if WT ( A1,A 2, yB ) > 14.23932

*" C ^a C ) =1

100 ^{- a} C ^{( A} _x , A 2, ^y B )

if 90 <  a ( A i, A 2, Ув ) <  100

if a C ( A1,A 2, yB ) >  100

Now linear membership and non-membership function for the constraint a _T ( A₁, A ₂, y B ) is defined as follows:

1                    if a T ( A 1, A 2, yB ) <  130

°a_c ^{( a} C ) =

^a_T ^{( a} T ) =■

150 - ^a T ⁽ A p A 2, ^y B )

if 130 <  a ( A_x , A ₂, y_B ) <  150

0                    if a; (A, A, УВ) < 90 + e ar. (A., A-,, yR) - (90 + e )

C ¹  2_n B ---------- f 90 + e ₂ <  a C ( A 1, A 2, yB ) <  100

^{10 - e} 2

1                           if a C ( A 1, A 2, yB ) >  100

'a ^{( a} T ) =

0                   if a T ( A p A 2, yB ) >  150

if a T ( A1, A 2, yB ) <  130 + E 1

a_T ( A , A , y „) - (130 + e )

T ¹  % B ---------^L if 130 + E 1 <  a T ( A1, A ₂ , yB ) <  150

20 — e^

1                         if a T ( A1 A 2, yB ) >  150

and linear membership and non-membership function for the constraint a C ( A 1 ,A ₂, y B ) is defined as follows:

Now IFO technique for NLP (2) with this membership and non-membership functions can be solving for different value of e , E 1 and e ₂ .The optimal solution of the NLP model (2) using intuitionistic fuzzy single objective nonlinear programming (IFNLP) technique is given in table 1. The solution obtained by Intuitionistic Fuzzy Non-linear programming (IFNLP) technique is compared with solution obtained by fuzzy non-linear programming (FNLP) technique of the same NLP model (2).

Table 1. Comparison of Optimal solution of (2) based on different method

Method	Design Variable A 1*( m 2)	Design Variable A 2*( m 2)	Y coordinate of node B y * B ( m )	Weight W * ( KN )
FNLP [18]	0.5567145	0.6780355	.8087956	13.38188
IFNLP	05482919	0.6692795	.8067448	13.19429

Here we get best solution for the tolerance e = 0.1, e = 8 and e = 4 , for non membership function of objective and constraints respectively. From the table 1, it shows that Intuitionistic Fuzzy Non-linear programming (IFNLP) technique gives better optimal result in the perspective of Structural Optimization.

• VII. Conclusions

In this paper we proposed an integrated approach in design optimization to deal with the uncertainty using the intuitionistic fuzzy set theory. From the Table 1, it shows that IFNLP technique gives better optimal solution of the weight of the planer truss bar .We finally conclude that IFNLP technique performs better than FNLP technique. The results of this study may lead to the development of effective IFO technique for solving other models of nonlinear programming problem in different fields.

The authors declare that there is no conflict of interests.

The authors are grateful for the valuable comments and suggestions from the respected reviewers which have enhanced the strength and significance of our work .It is privilege to thank my respected guide for his enormous support and encourage for the preparation of this research paper.

B164, 1970.

• [3]    K. Atanassov, “Intuitionistic fuzzy sets,” Fuzzy sets and Systems, 20,87-96, 1986.

• [4]    Werner,B., “Interactive fuzzy programming systems. Fuzzy sets systems, 23,133-178,1987.

• [5]    Xu, C. “Fuzzy optimization of structures by the two-phase method”,Computer and Structure, 31(4),575–580,1989.

• [6]    Yeh, Y.C, and Hsu, D.S. “Structural optimization with fuzzy parameters”.Computer and Structure, 37(6), 917–24, 1990.

• [7]    Angelov, P.P. Intuitionistic fuzzy optimization. Notes on Intutionistic Fuzzy Sets 1 (2), 123–129, 1995.

• [8]    K. Atanassov, “Idea for intuitionistic fuzzy sets equation, in equation and optimization,” Notes on Intuitionistic Fuzzy Sets, 1, 17-24, 1995.

• [9]    Angelov, P.P. Optimization in intuitionistic fuzzy environment. Fuzzy Sets and Systems 86, 299–306, 1997.

• [10]    K. Atanassov, “Two theorems for Intuitionistic fuzzy sets,” Fuzzy Sets and Systems, 110,267-269, 2000.

• [11]    Nicholas Ali, Kumaran Behdinan, Zouheir Fawaz, “Applicability and Viability of a GA based Finite Element Analysis Architecture for Structural Design Optimization,” Computers and Structures, 81, 2259

2271,2003.

• [20]    Nasseri, S.H.,Alizadeh, Z. “ Optimized solution of a two bar truss nonlinear problem using fuzzy geometric programming .Journal of Nonlinear Analysis and Application, 2014,1-9,2014.