Optimizing the CMTS to Improve Quality of Service in Next Generation Networks based on ACO Algorithm

Published Online April 2013 in MECS

In Next Generation Network (NGN), the backbone of the overall network architecture will be IP network, supporting different access network technologies such as wireless Local Area Network (WLAN), UMTS Terrestrial Radio Access Network (UTRAN), and WiMax. Moreover, this integrated wireless system, will have to handle diverse types of traffics: data traffics (e.g. web browsing, e-mail, ftp), voice traffic (e.g. voIP), and multimedia traffics (e.g. video conferencing, online TV, online games), etc... NGN will provide advanced services, such as Quality of Service (QoS) guarantees, to users and their applications.

However, current Internet routing protocols such as Open Shortest Path First (OSPF), Routing Information Protocol (RIP), and Border Gateway Protocol (BGP) are called " best-effort " routing protocols, which means it will try its best to forward user traffic, but can provide no guarantees regarding loss rate, bandwidth, delay, delay jitter, etc. It's intolerable for NGN services, for example video-conferencing and video on-demand, which require high bandwidth, low delay, and low delay jitter. And provide the different type of network services at the same time is very difficult. Thus, the study of Quality-of-

Service (QoS) is very important nowadays [1]. To provide QoS in NGN, many techniques have been proposed and studied, including Integrated Services [2], Differential Services [3], MultiProtocol Label Switching (MPLS) [4], Traffic Engineering and QoS-based Routing [1]. And most problems can be formulated as the optimization models, such as the network reliability optimization model, shortest path routing model and constrained minimum spanning tree (MTS) model etc.

In [5], Lin Lin et al focus on the network topological design for providing NGN’s QoS. The authors formulated the problem as a extended capacitated minimum spanning tree (cMST) problem, which the objective is minimizing the communication cost (defined as a kind of performance measures for NGN’s QoS) with considering the following constraint:

• •    Consider the capabilities of the network.

• •    Define different priority for different types of services.

• •    Dynamic environment.

As we know, this cMST is NP-hard problem. In addition, the complex structures, complex constraints of this problem to be handled simultaneously, which make the problem intractable to traditional approaches. There are many Evolutionary Algorithms (EAs) have been successfully applied to solve constrained spanning tree problems of the real-life instances; and also have been used extensively in a wide variety of communication network design problems. In [6], the author used traditional Prim’s algorithm (without considering the capacity constraint) to solve MST. G. Raidl and B.A. Julstrom in [7] proposed Edge Sets: An Effective Evolutionary Coding of Spanning Trees. Zhou and Gen presented a note on genetic algorithm approach to the degree-constrained spanning tree problems in [8-9]. The authors in [5] proposed a PrimPred-based Evoluation Algorithm to solving cMTS. They adopted PrimPred-based encoding, Prim-based crossover, LowestCost mutation, Immigration operators and a parameter autotuning strategy.

In the latest paper [10-11], we have introduced two algorithms based on Particle Swarm Optimization (PSO) and Ant Colony Optimization (ACO) to solve the optimal communication spanning tree (OCST) problem finds a spanning tree that connects all node satisfies their communication requirements for a minimum total cost.

In this paper, we proposed a new ACO algorithm approach to solve NGN’s QoS problem. Numerical experiments with various scales of communication network problems show the effectiveness and the efficiency of our approach by comparing with the recent researches. The experimental results show that our algorithms have achieved much better than previous algorithms.

The rest of this paper is organized as follows: Section II presents the problem formulation the capacitated minimal spanning tree. Section III summarized the several kinds of classification of encoding methods for developing an EA to network design problems. Section IV presents our new algorithm for the capacitated minimal spanning tree based on ACO algorithm. Section V presents our simulation and analysis results, and finally, section VI concludes the paper

• II.    Problem Formulation

Following [5], The communication network is modeled using an edge-weighted undirected graph G =( V , E , Q , U ) with n nodes and m edges. Fig.1 presents a simple network with 12 nodes and 40 edges.

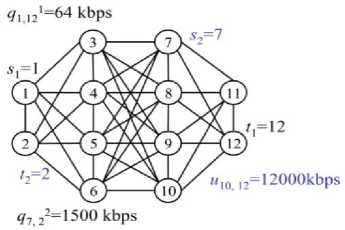
(a) Simple example of network

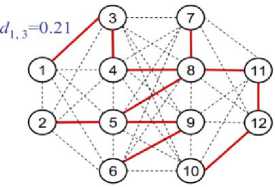
(b) A minimum spanning tree

Figure 1. A simple network with 12 nodes and 40 edges

The network data sets of 12 nodes and 40 edges defined in Table I.

The capacitated minimal spanning tree problem can be defined as follows:

Indices

• •    i, j, k=1, 2, ..., n , is index of node

• •    l=1..L is index of service type

Parameters

• •    n =| V is number of nodes

• •    m =| E | is number of edges

• •    q_st e Q is requirement of type l form source node

s to sink node t.

• •    u_y e U is capacity of edge ( i , j )

• •    w, e W is weight   (priority )  of type l

communication service.

• •    d_y e D is delay of edge ( i , j ) (or defined as a

kind of performance measures for NGN’s QoS), where dj-=E lwG (qj- j                  (1)

• •    G ( q l - Uy ) is function for delay defination of

service type l

Decision variables

• •    y j : the amount of requirement through arc( i , j )

• •    x ij : 0-1 decision variable

table i.    The network data sets of 12 nodes and

40 edges

k	Edge (i, j)	Weight wi j
1	(1, 2)	35
2	(1, 3)	23
3	(1, 4)	26
4	(1, 5)	29
5	(1, 6)	52
6	(2, 3)	34
7	(2, 4)	23
8	(2, 5)	68
9	(2, 6)	42
10	(3, 4)	23
11	(3, 7)	51
12	(3, 8)	23
13	(3, 9)	64
14	(3, 10)	28
15	(4, 5)	54
16	(4, 7)	24
17	(4, 8)	47
19	(4, 10)	24
20	(5, 6)	56
21	(5,7)	26
22	(5, 8)	35
23	(5, 9)	63
24	(5, 10)	23
25	(6, 7)	27
26	(6, 8)	29
27	(6, 9)	65
28	(6, 10)	24
29	(7, 8)	38
30	(7, 11)	52
31	(7, 12)	41
32	(8, 9)	62
33	(8, 11)	26
34	(8, 12)	30
35	(9, 10)	47
36	(9, 11)	68
37	(9, 12)	33

38	(10, 11)	42
39	(10, 12)	26
40	(11, 12)	51

Mathematically, the problem is reformulated as a capacitated Minimal Spanning Tree (cMST) model is as follows:

(п\^

min f ( x ) = L | L Wi ^ХГ |^mm { °, У у - « /у } ) l ⁽²⁾

(I,j)e E к i=1          X

Subject to:

nn

LL Xj = n -1(3)

■=1 у = 1

nn

LL xj < SI — 1 for any set S of nodes(4)

i = 1 у = 1

nn

L У у - L у *

j=1

q j , if i = s

= - 0, if i ' e V - { 5 , t }

^- q , ^if i = t

V ( 5 , t ) e source node and sink node of q j , V i e L

У j > 0, Vi, j = 1..n(6)

xj e{0,1}, Vi, j = 1..n(7)

where,

• •    The constraint (3) is a cardinality constraint implying that we choose exactly n-1 edges.

• •    The packing constraint (4) implies that the set of chosen edges contain no cycles (if the chosen solution contained a cycle, and S were the set of nodes on a chosen cycle, the solution would violate this constraint)

• •    The constraint (5) implies a flow conservation law depended communication requirement on the observed at each of the nodes other than sort.

• •    The constraint (7) implies the 0-1 variable x ij indicates whether we select edge ( i , j ) as part of the chosen spanning tree (note that if y ij >0 then x ij =1, else x ij =0).

• III.    Related works

How to encode a spanning tree T in a graph G is critical for developing an EA to network design problems, it is not easy to find out a nature representation. Because, designing an appropriate encoding method so as to build an effective EA.

In this section, we summarized the several kinds of classification of encoding methods as follows:

• •    Characteristic Vectors-based Encoding: used by Davis et al. (1993) [12], Bean (1994) [13],

  Piggott and Suraweera (1995) [14].

• •    Edge-based Encoding: used by Knowles and Corne (2000) [15], Raidl (2000) [16-17], Chou et al.(2001) [8], Raidl and Julstrom (2003) [7].

• •    Node-based Encoding: is discussed by Cayley (1889) [18], Zhou and Gen (1997, 1999, 2000) [19-21].

In [8], Chou et al predecessor-based encoding generates some chromosomes that are illegal (i.e., not a spanning tree). Combining the simple random initialization, most of the chromosomes will be illegal due to three reasons: missing node i , self-loop, or cycles. The complex repair process will be used at each generation (computational cost), and after repairing, the offspring of the crossover and mutation are difficult to represent solutions that combine substructures of their parental solutions (worst heritability and locality).

Lin Lin and Mitsuo Gen in [5], proposed a PrimPred-based encoding, improved predecessor-based encoding. The initialization depends on an underlying random spanning-tree algorithm. The detailed procedure of this PrimPred-based encoding and decoding is introduced in [22].

• IV.    Ant Colony Optimization for the cMST

• A.    Ant Colony Optimization

The ACO algorithm is originated from ant behavior in the food searching. When an ant travels through paths, from nest food location, it drops pheromone. According to the pheromone concentration the other ants choose appropriate path. The paths with the greatest pheromone concentration are the shortest ways to the food. The optimization algorithm can be developed from such ant behavior.

The first ACO algorithm was the Ant System [23], and after then, other implementations of the algorithm have been developed [24-25].

• B.    Solving the cMST based on ACO

In this section, we present application of ACO technique for the cMST problem. Our new algorithm is described as follows. We consider that configurations in the algorithm are sets of n nodes.

The encoding of the ant k configuration is matrix by means, say k = { x j } where x_y e { 0,1 } , V i , j = 1.. n . We use fully random initialization in order to initialize the ant population satisfied constraints (3) and (4). After that, the pheromone matrix y is generated with matrix elements that represent a location for ant movement, and in the same time it is possible receiver location.

We use real encoding to express an element of matrix У = { У у } where y_y > 0, V i , j = 1.. n and computed by the formula (5).

The next node is selected according to the probability with which ant k will choose to go from current node i to next node j is calculated by the following formula:

k pij

t

E h ] * [ n , ]'

l e N k

In which, Tj is the pheromone content of the path from node i to node j, N ^k is the neighborhood includes only nodes that have not been visited by ant k when it is at node i , η ij is the desirability of node j , and it depends of optimization goal so it can be our cost function.

The influence of the pheromone concentration to the probability value is presented by the constant α , while constant β do the same for the desirability. These constants are determined empirically and our values are α=1, β=10 .

The ants deposit pheromone on the locations they visited according to the relation.

new     current        k

T,  = T,    + At,

where A T k is the amount of pheromone that ant k exudes to the node j when it is going from node i to node j.

This additional amount of pheromone is defined by:

^AT ,

T ij

In which, d ij is delay of edge ( i , j ) (or defined as a kind of performance measures for NGN’s QoS) is computed by the formula (1). The cost function for the ant k is computed by the formula (2). The stop condition we used in this paper is defined as the maximum number of interaction N max ( N max is also a designed parameter).

The Fig.2 presents process of our algorithm to solve cMST based on ACO.

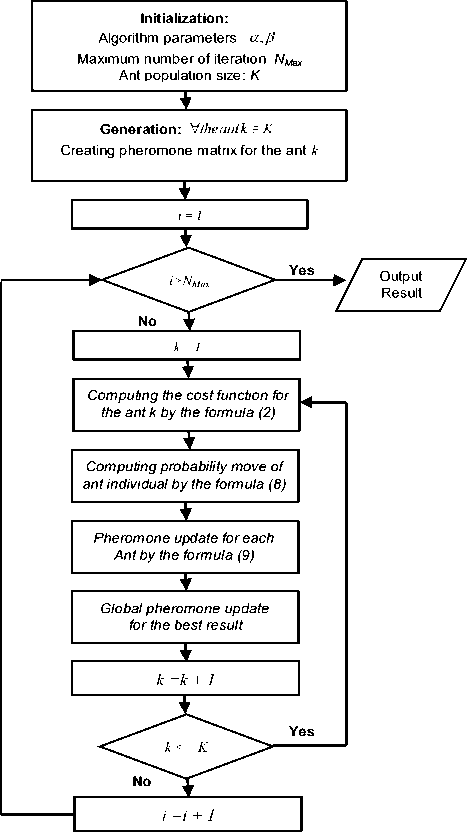
Figure 2. The ACO Algorithm’s flow chart

• V.    Experiments and Results

• A.    The problems tackled

For the experiments, we have tackled several cMST instances of different difficulty levels defined as follows:

We use the 3 complete network structures have 20 nodes (n=20) with 3 kinds of services:

• •    Type 1: Cable television.

• •    Type 2: IP phone.

• •    Type 3: Data

The weight (priority) of these 3 types respectively:

• •    w 1 =0.60

• •    w 2 =0.30

• •    w 3 =0.10.

The capacity of each edge ( i , j ) are represented as random variables depend on the uniform distribution: runif ( m , 100, 1000)

The 20 time-period requirements of different service types from node s to node t are represented as random variables depend on the distribution functions:

• •    Type 1: exponential distribution:

r * exp (| Q|, 0.03)

• •    Type 2: lognormal distribution:

0.1*r*lnorm(|Q|, 0.1, 0.1)

• •    Type 3: normal distribution:

r*norm(|Q|,0.01, 0.001)), where |Q|=100.

• B.    ACO algorithm specifications

In our experiments, we have already defined parameters for the ACO algorithm shown in Table II.

TABLE II.      the aco algorithm specifications

Ant Population size	K = 100
Maximum number of interaction	N Max = 500
Parameter	α=1, β=10

• C.    Numerical Results

In the experiment, our proposed ACO is compared with PrimPred-based EA [5] various evolutionary algorithms Edge-based EA [10], Prufer number-based GA [7] and traditional Prim’s algorithm (without considering the capacity constraint) [6].

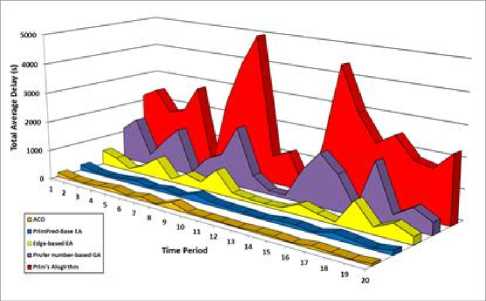
Figure 3.Comparisons total time average delay results of five Algorthms

The objective function is total time average delay of our algorithms has achieved a much better performance than other algorithms. The experimental results show in Fig.3.

• VI.    Conclusion and Future Work

In this paper, we have proposed an effective ACO algorithm for improvement of Quality of Service in Next Generation Network. We have formulated this problem as an extended capacitated minimum spanning tree (cMST) problem with considering capabilities of the network, different priority for different types of services and dynamic environment. In our algorithm, the objective functions are determined by the total average time delay based pheromone matrix of ants satisfies capacity constraints to find good approximate solutions.

Numerical experiments with various scales of communication network problems show the effectiveness and the efficiency show that our algorithm is much better than the recent researches. Optimizing quality of service in Next Generation Network with considering capabilities, different types of services, profit, coverage area and throughput maximization in dynamic environment is our next research goal.