Опыт конечно-элементной аппроксимации железобетонных балок-стенок с проемами

В настоящее время в практике проектирования строительных конструкций все шире применяются расчетные модели, учитывающие действительные свойства бетона и арматуры и особенности их работы под нагрузкой. До образования трещин бетон и арматура деформируются совместно, что позволяет определять матрицу жесткости железобетона путем суммирования матриц жесткости бетона и арматуры. При этом учитывается зависимость жесткостных параметров бетона от направления главных осей, так называемая приобретаемая ортотропия. После образования трещин совместность деформаций бетона и арматуры нарушается. В рамках деформационной модели [3] свойства железобетона с трещинами аппроксимируются свойствами некоторого эквивалентного сплошного анизотропного тела. При этом жесткостные параметры записываются в зависимости от схемы образования трещин и их ориентации относительно направления арматуры, а также учитываются сдвиг берегов трещин и неоднородность напряженного состояния бетона в полосах между трещинами. В предыдущих пуб- ликациях [4], [5] приводятся выражения для коэффициентов матрицы жесткости железобетона до и после образования трещин, а также результаты нелинейного расчета простейших экспериментальных конструкций методом конечных элементов с помощью разработанного авторами программного комплекса.

Дальнейшее совершенствование расчетной модели, а также изучение особенностей конечно-элементной аппроксимации потребовало привлечения в качестве объекта исследования реальных железобетонных конструкций в составе зданий и сооружений с различными схемами загружения и механизмами разрушения.

Для расчета по предложенной методике были выбраны три балки-стенки из опытов НИИ Мос-строя [2] высотой 2,8 м, толщиной 0,22 м и пролетом 5750 мм (рис. 1б), опирающиеся на колонны. Конструкции, использованные в виде опытных образцов, предназначались для восприятия вертикальных нагрузок от вышележащих этажей жилых зданий в том случае, когда на первых этажах зданий предусматривалось раз-

мещение объектов общественного назначения. По оси конструкции располагалось отверстие для пропуска инженерных коммуникаций.

Балки-стенки БС-1, БС-2, БС-3 имели одинаковые геометрические размеры, практически одинаковое армирование, но были изготовлены из тяжелого бетона существенно разной прочности (табл. 1).

Таблица 1

Физико-механические свойства бетона

Марка образца	Класс бетона	R b , МПа	R bt , МПа	E b , МПа
БС-1	B 15,5	20,4	1,9	25600
БС-2	B 10,8	14,2	1,4	16600
БС-3	B 29,1	38,2	2,65	29500

Таким образом, при испытании конструкций были реализованы различные схемы разрушения. Разрушение сжатой зоны балки-стенки БС-1 сопровождалось текучестью продольной арма- туры в пролете конструкции. При разрушении сжатой зоны балки-стенки БС-2 продольная арматура работала упруго. Балка-стенка БС-3 разрушилась из-за раздавливания бетона на опоре в результате действия дополнительной сосредоточенной силы, приложенной по оси опоры, при постоянной пролетной нагрузке.

На рис. 1а представлена расчетная схема балки-стенки. Симметричная часть балки-стенки была разбита на 120 прямоугольных конечных элементов, соединенных 143 узлами. Опорные элементы 111 и 112 имеют характеристики металла. Для каждого КЭ был определен тип жестко сти, который задан в соответствии с классом бетона и арматуры и коэффициентами армирования (рис. 2а, табл. 1, 2). Коэффициенты армирования определялись для каждого типа конечного элемента расчетной схемы в соответствии с шагом и диаметром арматурных стержней (рис. 2б).

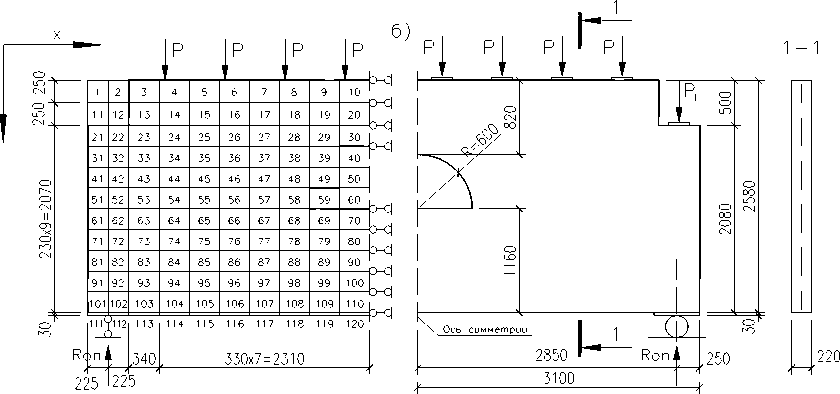
Рис. 1. а) расчетная схема балок-стенок; б) конструкция балок-стенок БС-1, БС-2, БС-3

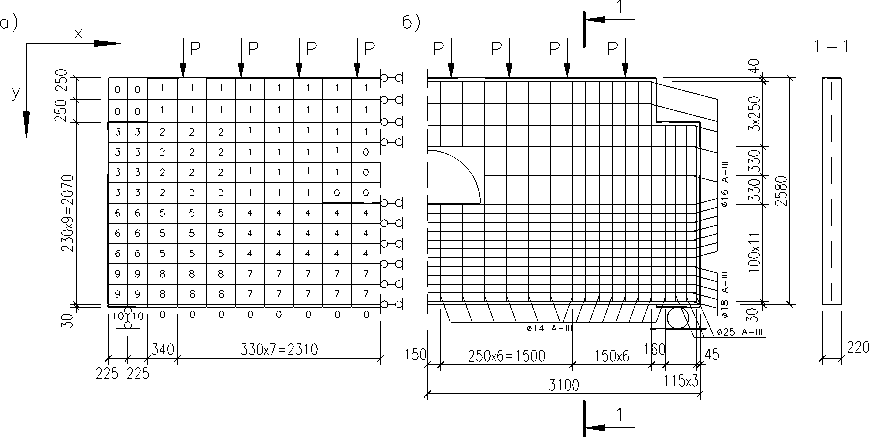
Рис. 2. а) нумерация типов жесткостей; б) армирование балок-стенок БС-1, БС-2, БС-3

Таблица 2

Физико-механические свойства арматуры БС-1, БС-2, БС-3

№ жесткости (рис. 2а)	Начальные деформативные характеристики арматуры		Прочностные характеристики арматуры		Коэффициенты армирования		Толщина балки-стенки, м
	Esx, МПа	Esy ,МПа	Rs,МПа	Rsu,МПа	μ x	μ y
0	–	–	–	–	–	–	0,22
1	207000	207000	429	590	0,0073	0,0047	0,22
2	207000	207000	429	590	0,0073	0,0093	0,22
3	207000	207000	429	590	0,0073	0,0397	0,22
4	207000	207000	429	590	0,0183	0,0047	0,22
5	207000	207000	429	590	0,0183	0,0093	0,22
6	207000	207000	429	590	0,0183	0,0397	0,22
7	207000	207000	429	590	0,0231	0,0047	0,22
8	207000	207000	429	590	0,0231	0,0093	0,22
9	207000	207000	429	590	0,0231	0,0397	0,22
10	207000	207000	429	590	1	1	0,22

В эксперименте нагружение образцов проводилось поэтапно с выдержкой на каждом этапе в течение 10–15 минут. При расчете шаг нагружения определялся с учетом постепенного увеличения нагрузки.

Шаг нагрузки был принят в размере 5 % от предполагаемого разрушающего усилия:

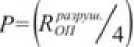
где P – сила, приложенная к конструкции (рис. 1, 2), R О ^р П ^азруш. – реакция опоры при предполагаемом разрушении конструкции.

Результаты расчетов балок-стенок по предложенной методике сопоставлялись с экспериментальными данными, данными линейно-упругого расчета и нелинейного расчета, выполненного по программе «Лира» версии 9.4 с учетом физической нелинейности железобетона по модели Г. А. Гениева [1].

Как показали расчеты, в результате нагружения балки-стенки БС-1 первые трещины появились в нижнем ряду конечных элементов (№ 108–110, рис. 1а) при суммарной нагрузке, равной 400 кН. Опытная нагрузка трещинооб-разования составила 385 кН. При этом угол направления главных осей n и t по отношению к осям x и y был равен 86°, что также соответствует опытным данным. На рис. 3 представлены расчетные и экспериментальные схемы развития трещин в балке-стенке БС-1. По мере увеличения нагрузки происходит развитие ранее образовавшихся трещин и появление новых, причем развитие трещин в опорной зоне сопровождается уменьшением угла их наклона к горизонтали. На рис. 4 показаны опытная кривая и теоретические графики прогиба конструкции, полученные по разным моделям. Как видно из графика, до образования трещин деформации конструкции носят преимущественно упругий характер. В дальнейшем деформирование конструкции приобретает выраженный нелинейный характер.

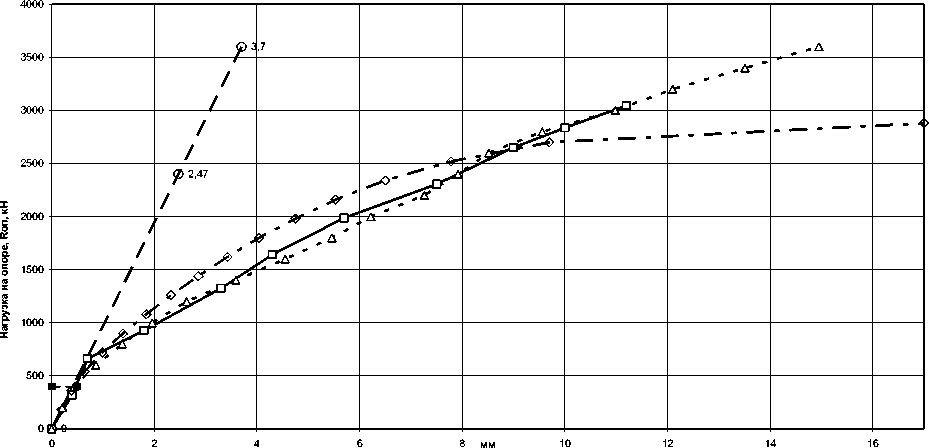
экспериментальные данные,    результаты по предлагаемой методике

Рис. 4. График прогибов в середине пролета (перемещения узла 132 по оси Y) в балке-стенке БС-1

Теоретическая кривая прогиба по предлагаемой модели по характеру деформирования полностью соответствует опытной с расхождением в отдельных точках до 7 %. Разрушение балки-стенки БС-1 происходит в результате текучести арматуры растянутой зоны (18-й шаг нагружения, элементы № 108–110), что соответствует опытным данным.

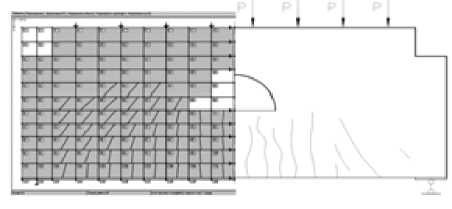
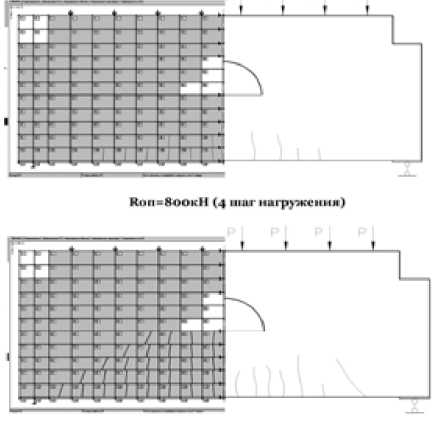
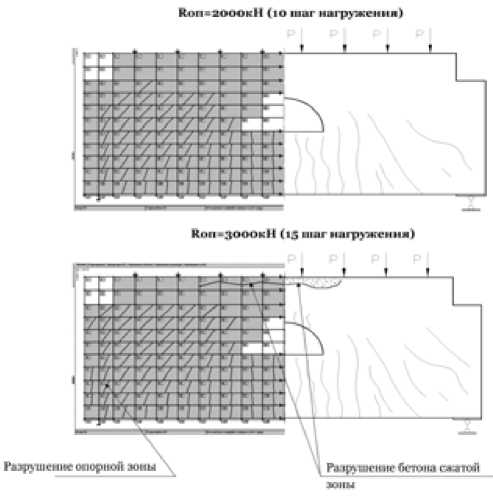
Во второй экспериментальной балке-стенке БС-2 первые трещины появились в нижнем ряду конечных элементов (№ 108–110) при суммарной нагрузке, равной 400 кН. Опытная нагрузка трещинообра-зования составила 377 кН. На рис. 5 представлены расчетные и экспериментальные схемы развития трещин в балке-стенке БС-2. Как и в первом опыте, по мере увеличения нагрузки происходит развитие трещин и появление новых. На рис. 6 показаны опытная кривая и теоретические графики прогиба конструкции, полученные по разным моделям.

Коп-4<>окН (нагрузки TpeiHMiiocfApe-KHieHU*)

Ron = 1200 кН (6 шаг ншр^икения)

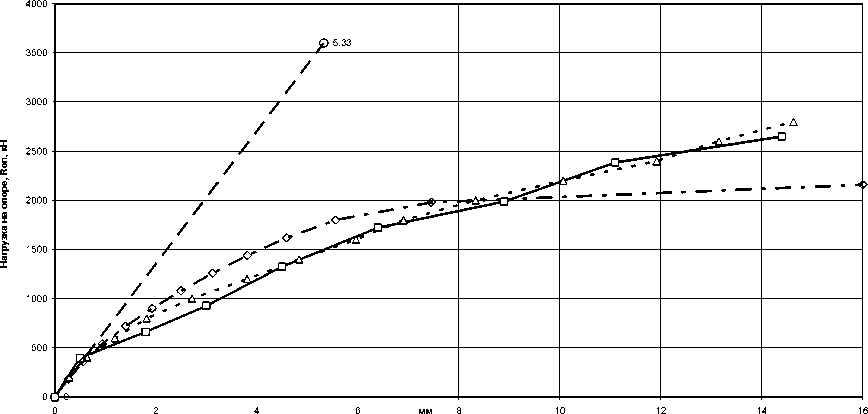
экспериментальные данные, результаты по предлагаемой методике

Рис. 6. График прогибов в середине пролета (перемещения узла 132 по оси Y) в балке-стенке БС-2

Теоретическая кривая прогиба по предлагаемой модели по характеру деформирования полностью соответствует опытной с расхождением в отдельных точках до 10 %. Разрушение балки-стенки БС-2 происходит в результате разрушения бетона сжатой зоны (шаг нагружения 15, элементы № 7–10), что соответствует опытным данным.

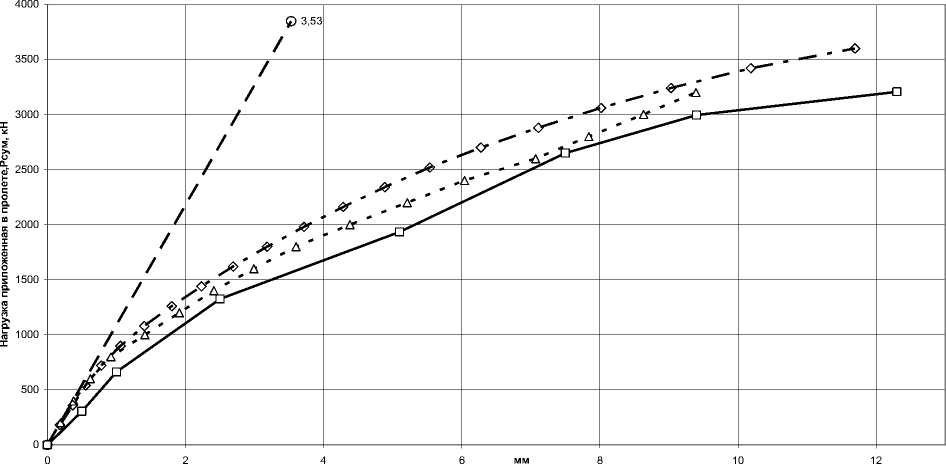
В балке-стенке БС-3 первые трещины появились в нижнем ряду конечных элементов (№ 106–110) при суммарной нагрузке, равной 600 кН. Опытная нагрузка трещинообразования составила 564 кН. На рис. 7 представлены расчетные и экспериментальные схемы развития трещин в балке-стенке БС-3. При увеличении нагрузки происходит развитие трещин и появление новых. На рис. 8 показаны опытная кривая и теоретические графики прогиба конструкции, полученные по разным моделям. Как видно из графика, до образования трещин деформации конструкции носят преимущественно упругий характер. В дальнейшем деформирование конструкции приобретает выраженный нелинейный характер.

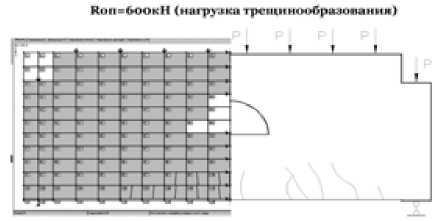
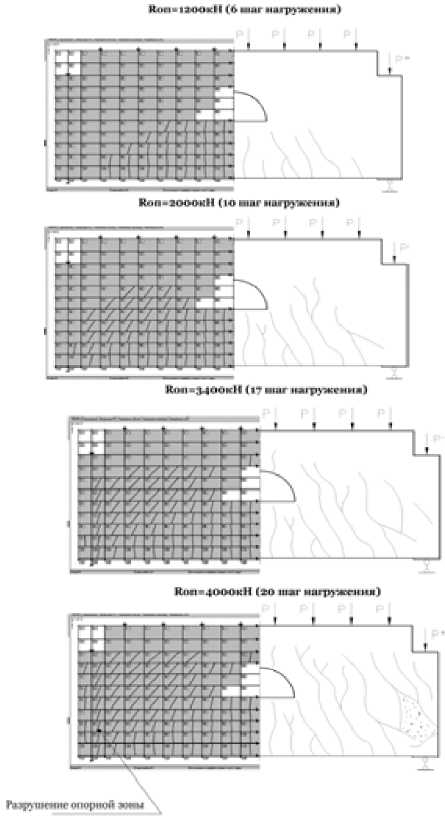
Результаты расчетов автора                  Экспериментальные данные                  Результаты упругого расчета                  Лира 9.4 R7*

экспериментальные данные, результаты по предлагаемой методике

Рис. 8. График прогибов в середине пролета (перемещения узла 132 по оси Y) в балке-стенке БС-3

Теоретическая кривая прогиба по предлагаемой модели по характеру деформирования полностью соответствует опытной с расхождением в отдельных точках до 15 %. Разрушение балки-стенки БС-3 происходит в результате исчерпания прочности опорной части конструкции (20-й шаг

нагружения, элементы № 31–32, 41–42, 51–52, 61–62, 71–72, 81–82, 91–92, 101–102), что соответствует опытным данным.

Работа выполнена при финансовой поддержке РФФИ.