Опыт применения модели состояния трубопровода высокого давления для оптимизации технического обслуживания

Стальные трубопроводы высокого давления на тепловых электростанциях эксплуатируются в условиях высоких нагрузок, в связи с чем элементы таких трубопроводов подвергаются риску возникновения различных повреждений. Поэтому своевременной диагностике этих повреждений уделяется большое внимание.

Повреждающие факторы, механизмы развития повреждений, типы дефектов и методы их выявления известны и классифицированы. В основном своим происхождением они обязаны усталостным трещинам и дефектам сварки. Для их своевременного выявления определены периодичность и объемы контроля [1]. Но анализ статистики повреждений трубопроводов [2] показывает, что даже при 100-процентном выполнении всех требований нормативно-технических документов (НТД) фиксируются случаи остановов трубопроводов.

Причина заключается в том, что требования НТД рас-счит аны на условно-идеальный трубопровод. То есть считается, что при монтаже и эксплуатации выполнены все требования проектной документации. Практика показывает, что учесть все отклонения от требований при монтаже и эксплуатации трубопровода невозможно. Это суммарное отклонение, как правило, проявляется в виде преждевременного развития дефектов. То есть, промежуток времени между проведением контроля состояния оказывается больше времени необходимого для развития дефекта до уровня, препятствующего надежной эксплуатации.

Предотвратить влияние этого «суммарного отклонения» можно двумя способами. Первый – поиск и устранение всех факторов, ускоряющих появление и развитие дефектов. Второй – уменьшение межконтрольного промежутка для своевременности выявления возникающих при эксплуатации дефектов.

Первый путь, хотя и позволяет решить проблему в корне, но во-первых, требует больших затрат на обследование, расчеты, привлечение специализированных организаций, во-вторых, не гарантирует результат в связи с тем, что факторов, влияющих на величину «суммарного отклонения» может оказаться гораздо больше, чем предполагалось вначале.

Второй путь также требует увеличения затрат, так как уменьшение межконтрольных промежутков ведет к увеличению простоя трубопровода. Нахождение оптимального значения таких промежутков есть решение задачи обеспечения надежности при минимизации затрат. Решить задачу оптимизации можно путем разработки математической модели состояний трубопровода и исследования зависимостей, которые она описывает.

Накопление отклонений от требований конструкторской и нормативно-технической документации в процессе эксплуатации трубопровода перерастает в возникновение отказа. Из-за большого количества факторов, влияющих на появление отказа, его значение приобретает характер случайной величины. Поэтому для создания математической модели состояния трубопровода можно применить вероятностные методы.

При заданном уровне надежности (вероятности P ₁ ) и известной интенсивности отказов λ оптимизирующими параметрами системы технического обслуживания трубопроводов являются периодичность и продолжительность технического обслуживания, t _ТО и τ_ТО .

Выполнив все необходимые преобразования, получим систему уравнений вида

ГX-1

II

P = 2 + Xtt 0 + -ТО

¹ l ^ТО t _ТО    1 + Xt _ТО J

- 1

P2 = ттo I X + — I x l tТО J

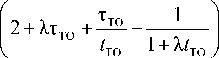
^X t ТО I T            , ^ТТО         ¹

--------1 2 + ЛТ то +

P 3 =

1 I X/ 1 то l                  t то    1 + X tt ТО

Используя полученные зависимости, можно построить аналитическую зависимость Р ₁ от оптимизирующих параметров t _ТО , τ_ТО .

Результаты расчетов по формуле (1) представлены в виде графиков зависимости вероятности готовности объекта Р ₁ к работе от периодичности обслуживания (рис. 1 а , б ), где видно наличие экстремума на графиках для любых τ_ТО и λ . Это означает, что исходя из математической модели состояний трубопровода и с учетом собранной статистики отказов, существует наиболее оптимальное соотношение периодичности и продолжительности обслуживания трубопровода, позволяющее добиться максимально возможного значения вероятности готовности к работе трубопровода. Или, другими словами, его работоспособности.

При увеличении периода tТО , с одной стороны, увеличивается вероятность скрытого отказа до проведения технического обслуживания, однако, с другой стороны, уменьшается доля времени на техническое обслуживание в общем ресурсе и, тем самым, увеличивается вероятность состояния готовности трубопровода к использованию. Изменением степени влияния этих двух факторов и обусловлено наличие экстремума на графиках зависимостей.

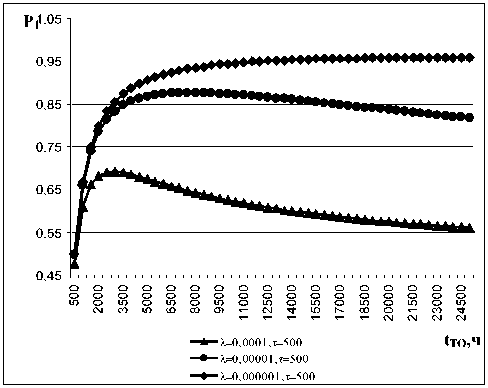
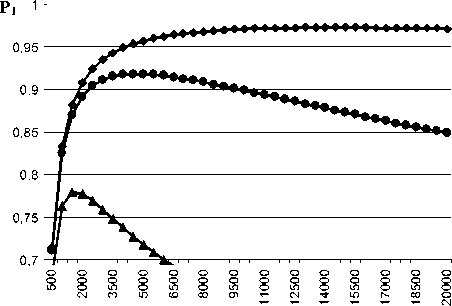
—*— Л=0,0001,т=200                       ( ТО ч

λ=0,00001,τ=200 λ=0,000001,τ=200

б

Рис. 1. Зависимость вероятности готовности к работе трубопровода от периодичности техобслуживания при заданных интенсивности отказов λ и продолжительности техобслуживания τ

При решении прямой задачи оптимизации (обеспечения требуемого значения вероятности P ₁ при минимальных потерях и затратах на техническое обслуживание) может быть необходимо, например, по известным или заданным значениям P ₁ и λ, а также одному из параметров системы технического обслуживания τ_ТО или t _ТО , определить второй параметр или подобрать значения τ_ТО или t _ТО , обеспечивающие наименьшие затраты. При решении обратной задачи оптимизации (обеспечение максимального уровня надежности), как правило, необходимо подобрать такие параметры τ_ТО или t _ТО (или один из них), которые при известном значении λ обеспечивают максимальное значение P ₁ при условии соблюдения некоторых (обычно экономических) ограничений. Варианты постановки задачи оптимизации достаточно многообразны, однако ее численное решение на основании построенной математической модели обычно не вызывает затруднений.

Анализ математической модели трубопровода позволяет:

– принимать решения, отвечающие наилучшим образом технической политике, проводимой на предприятии, в результате рассмотрения различных зависимостей основных параметров надежности трубопровода;

– решать вопрос обоснованности выделенных средств на техническое обслуживание трубопровода при заданной его готовности к работе; действительно, КПД работающего трубопровода не может превышать величины, определяемой соотношением k=

T нароботки

T календарное

= P 1 ( t ),

T = P ( t ) T        ;

наработки      1      календарное ;

– классифицировать трубопроводы на предприятии по трем видам состояния, с дальнейшей классификацией по следующим элементам:

• а)    состоянию готовности к работе с вероятностью P 1 ( t );

• б)    состоянию проведения технического обслуживания (диагностика, ремонт);

• в)    состоянию скрытого отказа (отказа, обнаруженного персоналом или средствами контроля спустя определенное время после его возникновения).

Проиллюстрировать применение этого метода можно на примере трубопровода горячего промперегрева (ГПП) энергоблока № 2 Красноярской ГРЭС-2. Трубопровод ГПП, предназначенный для транспортировки пара от котлоагрегатов к турбоагрегату, изготовляется из стальных труб (марка 12ХМФ) типоразмера 426 × 18 мм, 377 × 17 мм, 273 × 11 мм и представляет собой сложную объемно-пространственную конструкцию. Эксплуатируется с 1962 г. За это время трубопровод наработал 254 283 ч при 472 пусках, на параметрах эксплуатации Т = 545 ° С и P = 2,75 МПа. Трубопровод насчитывает 491 конструктивный элемент, сварных соединений 248 шт., из них угловых сварных – 92 шт.

Согласно накопленной статистике самый повреждаемый элемент трубопровода – угловые сварные соединения. В периоды ремонтных кампаний во время выполнения мероприятий по контролю металла было выявлено 15 дефектов типа «усталостная трещина» и «дефект сварки».

В октябре 2005 г. произошел неплановый останов энергоблока № 2 по причине образования сквозной трещины в околошовной зоне сварного соединения № А-42. Наработка с момента последнего контроля составила 23 855 ч. В соответствии с требованиями [1] межконтрольный промежуток составляет 50 000 ч. Таким образом, требования НТД были выполнены в полном объеме, но это не смогло предотвратить неплановый останов энергоблока. Значит, на возникновение и развитие трещины повлияли факторы, ускоряющие этот процесс. И хотя механизм возникновения и развития дефектов такого типа известен, выявление факторов, ускоривших процесс может потребовать больших затрат.

На основании собранных данных дефектоскопии можно рассчитать интенсивность отказов λ . Зная продолжительность контроля этих сварных соединений можно проанализировать вероятность готовности к работе трубопровода с помощью зависимостей, представленных в формуле (1).

Интенсивность отказов рассчитана по формуле

n ( t ) N ср Δ t ^,

λ( t ) =

где n(t) – число отказов за промежуток времени; Nср – среднее число исправно работающих элементов за тот же промежуток времени:

n ( t ) = 15 при Δ t = 254 283 ч,

Nср = 77, тогда

λ( t ) = 0,000 000 766 1.

Аналитическая зависимость вероятности готовности к работе Р ₁ от периодичности диагностирования t _ТО при заданных условиях показана на рис. 2.

Значения вероятности Р ₁ для различных значений периодичности технического обслуживания представлены в таблице .

Максимальное значение вероятности Р ₁ = 0,982 796, полученное в результате расчетов, соответствует периодичности технического обслуживания t _ТО = 11 500 ч. С учетом погрешности 3...5 % доверительный интервал составляет от 10 925 до 12 075 ч. То есть, проводя техническое обслуживание с рассчитанной периодичностью, можно получить максимальное значение вероятности готовности к работе трубопровода горячего промперег-рева энергоблока № 2.

Практика контроля аналогичных трубопроводов на энергоблоках №№ 1, 4 показывает, что при периодичнос- ти контроля один раз в 10 000...15 000 ч выявляются все дефекты подобного характера, что обеспечивает надежную работу трубопроводов в межконтрольный период.

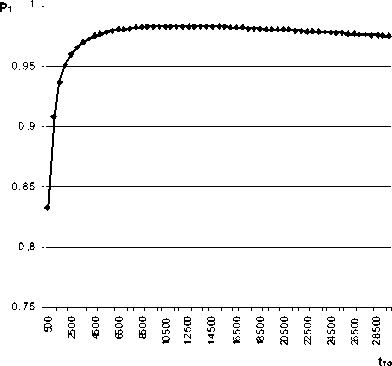
Рис. 2. Зависимость Р ₁ от периодичности технического обслуживания (диагностирования) при l = 0,000 000 766 1 ч^-1

Применение этого метода для расчета периодичности контроля относительно других типов повреждений, с учетом статистики отказов по каждому типу дефектов, позволит достаточно эффективно адаптировать существующую нормативно-техническую документацию для каждого конкретного трубопровода.

Вероятность возникновения отказа трубопровода ГПП энергоблока № 2 Красноярской ГРЭС-2

t то (ч)	τ то (ч)	λ (ч–1)	P 1
1 000	100	0,000 000 766 1	0,908 395
2 000	100	0,000 000 766 1	0,950 926
3 000	100	0,000 000 766 1	0,965 528
4 000	100	0,000 000 766 1	0,972 638
5 000	100	0,000 000 766 1	0,976 665
6 000	100	0,000 000 766 1	0,979 126
7 000	100	0,000 000 766 1	0,980 684
8 000	100	0,000 000 766 1	0,981 674
9 000	100	0,000 000 766 1	0,982 284
10 000	100	0,000 000 766 1	0,982 628
11 000	100	0,000 000 766 1	0,982 778
12 000	100	0,000 000 766 1	0,982 782
13 000	100	0,000 000 766 1	0,982 675
14 000	100	0,000 000 766 1	0,982 481
15 000	100	0,000 000 766 1	0,982 218
16 000	100	0,000 000 766 1	0,981 898
17 000	100	0,000 000 766 1	0,981 532
18 000	100	0,000 000 766 1	0,981 129
19 000	100	0,000 000 766 1	0,980 693
20000	100	0,000 000 766 1	0,980 231
21000	100	0,000 000 766 1	0,979 747
22000	100	0,000 000 766 1	0,979 243
23000	100	0,000 000 766 1	0,978 723
24000	100	0,000 000 766 1	0,978 189
25000	100	0,000 000 766 1	0,977 642
26000	100	0,000 000 766 1	0,977 085
27000	100	0,000 000 766 1	0,976 519
28000	100	0,000 000 766 1	0,975 945
29000	100	0,0000007661	0,975 363