Опытное исследование аэро- и гидравлической систем прямоточного котла на лабораторном стенде путем внедрения автоматического управления устройствами и сбора данных
Автор: Осинцев Константин Владимирович, Кускарбекова Сулпан Ириковна, Савостеенко Никита Вадимович, Максимов Никита Максимович
Журнал: Вестник Южно-Уральского государственного университета. Серия: Энергетика @vestnik-susu-power
Рубрика: Теплотехника
Статья в выпуске: 2 т.22, 2022 года.
Бесплатный доступ
Существует мало лабораторных стендов, которые имитируют работу прямоточных котлов, в то время как процессы, происходящие в таких устройствах, относятся к сложным в гидравлическом и теплофизическом аспектах. Изучив гидродинамику теплоносителя в цилиндрическом сложнонавитом змеевике, можно повлиять на производительность котла. Движение воздуха через подобный змеевик также представляет интерес для интенсификации процесса теплообмена в паровых прямоточных котлах. Современные приборы автоматизации могут позволить снять показания теплоносителя и воздуха с высокой точностью, а также передать экспериментальные значения на персональный компьютер для сохранения и последующего анализа данных. В статье представлены результаты по проектированию и сборке лабораторного стенда, который предназначен для опытного исследования аэро- и гидравлической систем прямоточного котла с помощью автоматического управления устройствами и сбора данных. Отображены результаты моделирования и экспериментальных данных.
Прямоточный котел, лабораторный стенд, число рейнольдса, коаксиальный змеевик
Короткий адрес: https://sciup.org/147238154
IDR: 147238154 | УДК: 621.18 | DOI: 10.14529/power220209
Текст научной статьи Опытное исследование аэро- и гидравлической систем прямоточного котла на лабораторном стенде путем внедрения автоматического управления устройствами и сбора данных
Прямоточные паровые котлы змеевикового типа применяются в промышленности, в жилищной сфере, в строительстве с XX века. Ярким примером служит парогенераторная установка КПА-500Ж. Модельный ряд котлов змеевикового типа претерпел ряд качественных изменений: расширилась линейка за счет увеличения площади теплообмена – увеличения диаметра и количества витков, сложность навивки труб. Условия обслуживания змеевиков остаются затрудненными, при ремонте змеевик необходимо менять полностью, так как частичная замена не всегда возможна и нерентабельна. Уровень аккумулятивной способности подобных котлов близок к нулю из-за конструктивных особенностей: теплоноситель совершает в змеевике один ход и далее поступает потребителю. Однако за короткое время теплоноситель совершает фазовое превращение из воды в пар, тем самым представляя научный интерес, как и перспектива интенсификации парообразования в паровых прямоточных котлах с улучшением работоспособности и обслуживания данных устройств [1].
Постановка задачи
На лабораторном стенде необходимо выполнить симуляцию гидравлического процесса движения теплоносителя по змеевику прямоточного котла. При конструировании необходимо принять упрощенную версию змеевика в виде цилиндрической формы, который является геометрически подобным внешнему змеевику сравниваемого котла модели КПА-500Ж [2].
Моделирование аэродинамической системы стенда заключается в наблюдении и фиксировании значений скорости воздуха, протекающего между витками змеевика, который помещен в цилиндр. Данная модель имитирует движение дымовых газов между змеевиками в прямоточном котле.
Для конструирования и сборки лабораторного стенда, который повторяет работу прямоточного котла змеевикового типа в режиме холостого хода без нагрева теплоносителя, необходимо выполнить следующие задачи.
-
1. Лабораторный стенд должен включать две системы: гидравлическую и аэродинамическую. Итоговыми опытными данными должны быть:
-
- расход теплоносителя (м3/ч) при известных значениях скорости насоса (об/мин) и давления в змеевике (МПа);
-
- объемный расход воздуха (м3/ч) на трех этапах прохождения по длине цилиндра (вход, середина и выход).
-
2. Алгоритм работы обеих систем стенда должен быть простым и интуитивно понятным для работы как в научных, так и в образовательных целях для студентов.
-
3. Проектирование электрической схемы.
-
4. Проектирование тепломеханической схемы.
-
5. Подбор гидравлического и электрического оборудования, а также проектирование по металлоконструкции должны быть выполнены с учетом выполнения условий подобия.
-
6. Монтаж и наладка оборудования.
-
7. Сбор и анализ данных.
Теоретическая часть
Математическая модель
В лабораторном стенде применяются трубы, изогнутые по винтовой линии, – змеевик. На каждую частицу жидкости, которая движется по изогнутой трубе, действует центробежная сила. Эта сила тем больше, чем больше скорость частицы. Под действием сил частицы в центре трубы движутся к стенке, а частицы у стенки, вытесняемые частицами, проникшими из середины трубы, движутся к центру кривизны. По ранее проведенным теоретическим и экспериментальным исследованиям параметр К, введенный Дином, определяет влияние кривизны при ламинарном течении:
-
К = «^ (1)
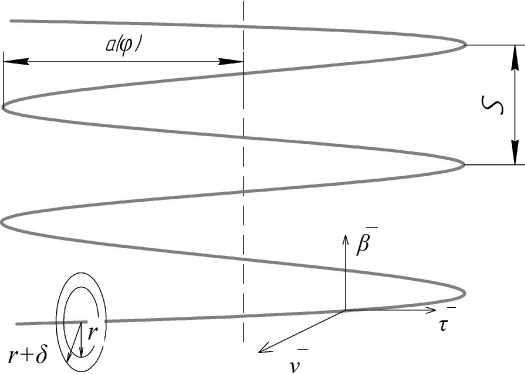
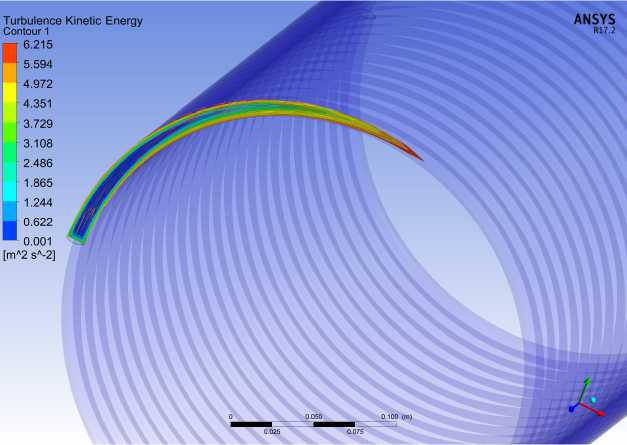
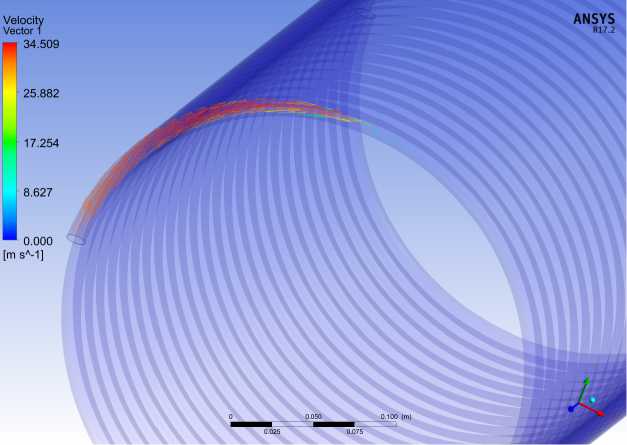
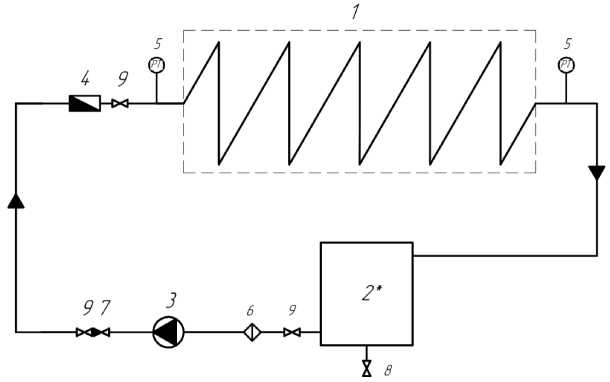
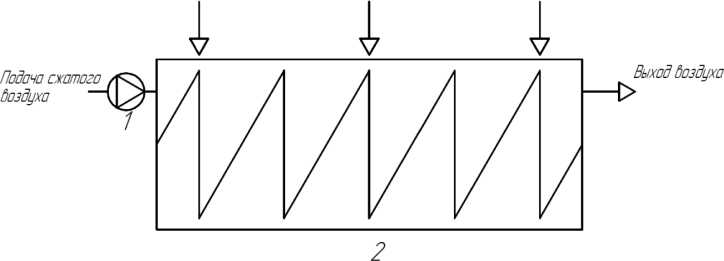
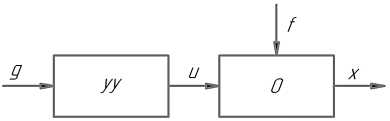
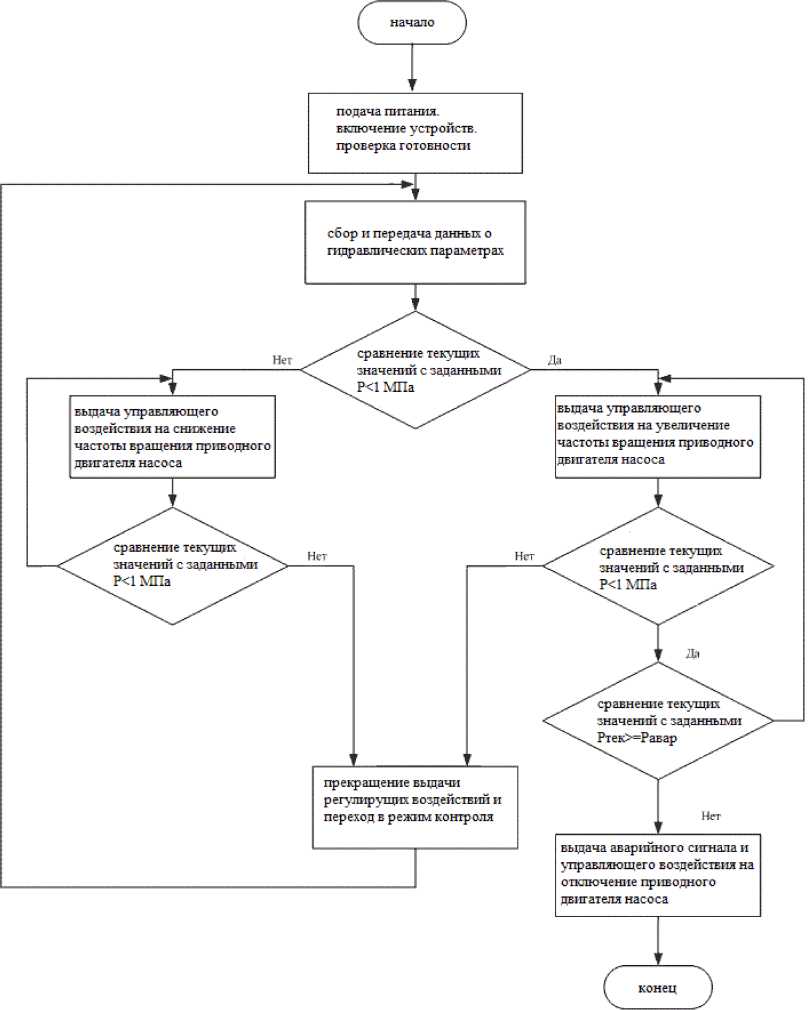
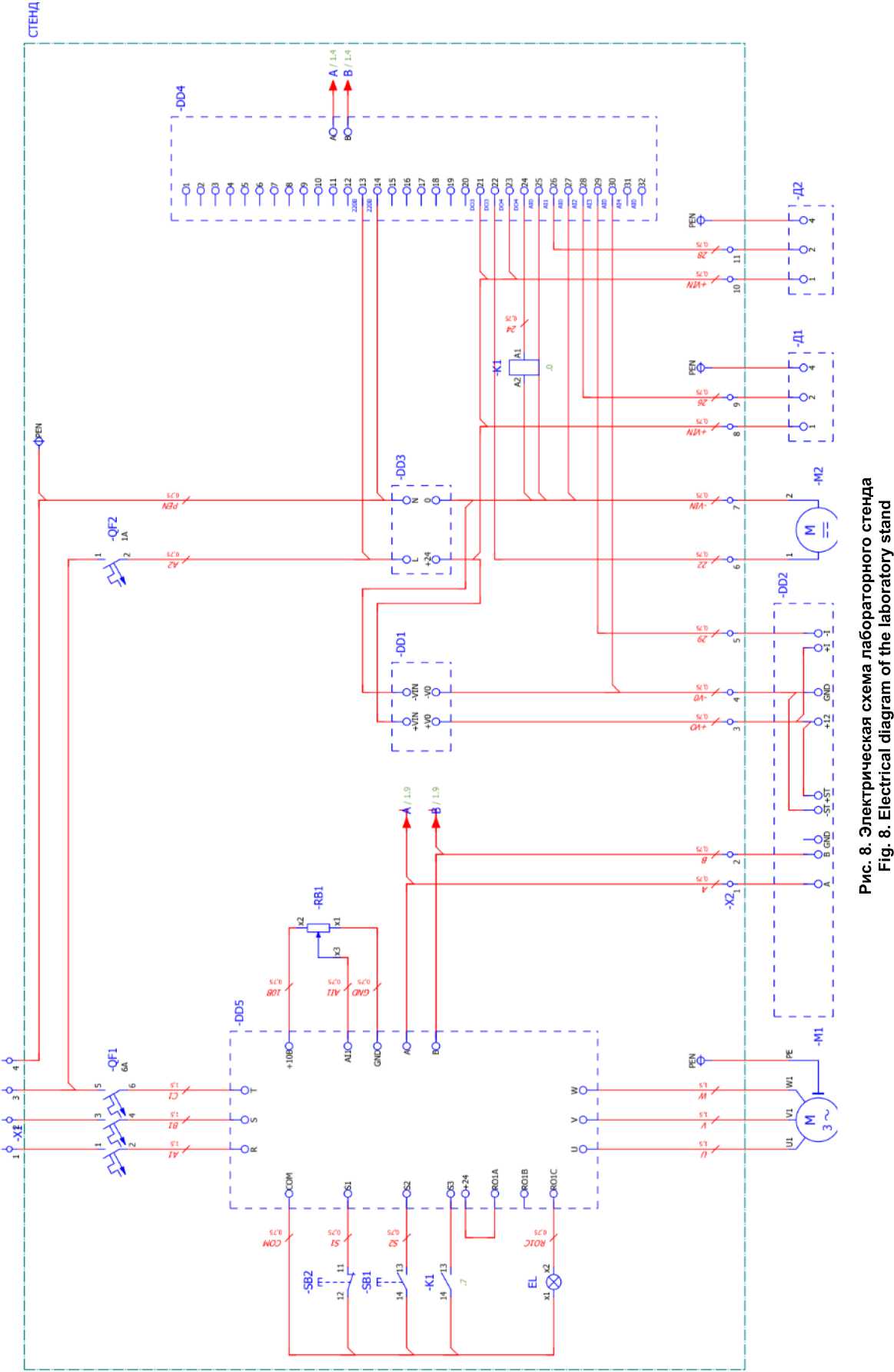
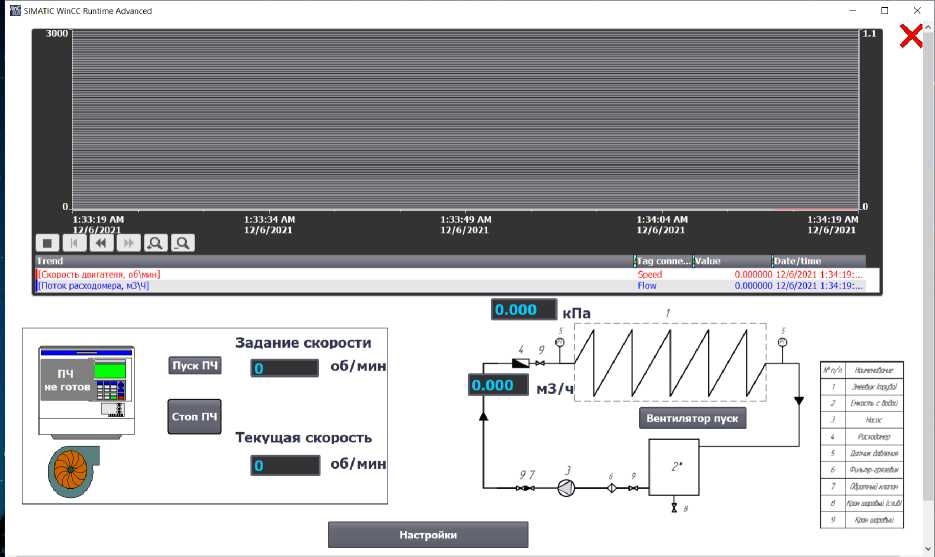
где Re = О = 2R, R - радиус кривизны змеевика; d - диаметр трубы (рис. 1). При K > 1,35 кривизна трубы не оказывает влияние на характер движения жидкости. Следовательно, ReKp = 13,5^. Однако это справедливо для малых соотношений d/D [3]. При 3 < R/d > 200, R = 0,50, величина критического значения числа Рейнольдса рассчитывается как [3, 4]: /r\~0,3 ReKp = 1500 g) . (2) Рис. 1. Схема змеевика Fig. 1. Coil diagram При турбулентном течении в изогнутых трубах из-за закрутки потока за счет вторичных течений увеличивается перемешивание, коэффициент теплоотдачи выше, чем в прямых трубах. Переход ламинарного течения в турбулентное в змеевиках при [5, 6]: 0,32 ReKp = 2^104(^) . (3) По моделируемому змеевику параметры D и d выполнены на пограничных условиях так, чтобы кривизна влияла на режим течения жидкости в трубе, но при этом можно принять, что в потоке отсутствует поперечная циркуляция и движение жидкости принято осесимметричным. Принято, что движение несжимаемой жидкости имеет стационарный, изотермический и турбулентный характер. Плотность, теплоемкость и коэффициент теплопроводности при движении теплоносителя не изменяется. С целью использования геометрической симметрии змеевиковых каналов и предполагая, что радиус изгиба змеевика много больше диаметра канала, используем специальную ортогональную систему координат, связанную с осевой винтовой линией с постоянной величиной радиуса изгиба, определяемой уравне- нием, учитывая отношение кручения к кривизне трубы [7]: /)(ф) = а(ф)е(ф) + Крк. В координатной форме уравнение (2) в следующем виде: (х = а(ф) cos ф; у = а(ф) sin ф; z = ^Кф, где рТ (ф) - радиус-вектор точки на осевой линии; е(ф) = Т cos ф + j sin ф; l,~j, к - орты декартовой системы координат; к - единичный вектор, направленный по оси z; ф - параметр винтовой линии; ^ - введенный параметр, учитывающий угол подъема витка. Данный параметр в дальнейшем не учи- тывается для упрощения решения; s К = —, S - шаг винтового канала; 2и ’ а(ф) - радиус изгиба оси винтовой линии (рис. 2). Рис. 2. Система координат: S - шаг, а(ф) - радиус изгиба, г - радиус трубы, 6 - толщина трубы Fig. 2. Coordinate system: S - the pitch, а(ф) - the bending radius, г - the radius of the pipe, 6 - the thickness of the pipe Определяя векторы сопровождающего репера для данной осевой линии змеевика и используя их в качестве базисных векторов т, р,^у, получим новые переменные Ь,ф,ф, которые связаны с переменными декартовой системы координат х,у, z, соотношениями [8-10]: (х = а(ф) cos ф + Ь(пх(ф) cos(ф + 0(ф)') + рх(ф) sin(ф + 0(ф))); у = а(ф) sin ф + Ь(пу(ф') ф cos(ф + 0(ф) + Ру(ф) sin( ф + 0(ф))); (6) z = Кф + Ь(п2(ф) ф cos(ф + е(ф)) + р^ф) sin(ф + е(ф))), из которых в случае постоянного радиуса изгиба канала о(ф) = а0 получаются выражения для векторов сопровождающего репера: а053(ф)+к1< т = I ; J^O+K2 Л -Кд(ф) + аок р = —I jK^+a^ V = е(ф); к(ф) = эK 7 = const, K2+a2’ где д(ф) = -I sin ф +; cos ф; к(ф) - кручение осевой линии канала. Для данной системы координат Ь, ф, ф имеем следующие характеристики [11]: 1) коэффициент Ляме (при постоянном радиусе): Нф = <о + К ■ (1 - (^ ■ cos(ф + 0)); 2) ненулевые символы Кристоффеля: р ф ‘фф 1 нф Энффф _ ф _ 1 ЭНф ■ Эф , ‘фф= ‘фф = Нф* Эф; р ф ‘ фЬ ф=^.ан,ф ф =ф= 1. ‘ьф нфэь ’ ‘фЬ‘Ьфь; рф ‘фф Ь2 гь ——н .^^ гф. = Эф , *фф Нф ЭЬ, ‘фф Ь. Таким образом, в выбранной системе уравнение движения, неразрывности и переноса количества энергии записывается следующим образом [12]: р [нфг^ (эф(НФЬv<»>v<»>)+эфtНФЬv<»>v<ф>))]+р [нф;(;iЬ:(Н^Ьv<ь>v<Ф>))- v<»>v<»>^;5!] = — — ЭР । 1 I Э С и кт Эд--!(н2Т AIi 1 f ® СКИ2Т 'Л _ т 1 Эн<Р. Эф +нфьуЭф(НфЬТ<фР>) +^ф^НфТ<фР>)1 +нфЬ(ЭЬ^ЬНфТ<ЬР>)) Т<фф>нфЭф; р[нфг^ (i^(ь!v<ф>v<ф>) +Эф(НфЬv<ф>v<ф>))] + р h;1„ I эЬ <нфЬ!v<ь>v<ф>))- v<Р^v<Р^^ЭНг] = = -5+нф;(:^ (Ь2г<фф>) + ^ (нфЬг<фф>)) +нф;(^(Ь!Нф г<ьф>)) • »|н1„ • (Э'„ <Ьг-фг-ь. > + Эф (нф ■..'/. <| + р [нф; (£(н, bvt^vtb,)) - т 1 ЭНф, {<фф>нфЭф; - v<ф>v<ф>нФЭЭг-v<ф>v<ф>i] = _ ЭР 1 I Э А । Э (и т 1 (Э т 1 Энф = ЭЬ +нфЬ \Эф (ЬТ<фЬ>) +Эф (Нф Т^)I+нфЬ (эь(ЬНф Т<-ЬЬ>)) Т<фф> нф ЭЬ эф(рvФ ь)+эф(рvvнф)+э;-ь(рvьнФь) = 0, - Т, . i- 1 <фф) ; где Т(у) = 2^0^, (i = Ь,ф,■ф; j = Ь,ф/ф") - физические компоненты девиатора тензора напряжений; д - вязкость с учетом турбулентности; V(i>, (i = Ь, ф, ф) - физические компоненты вектора скорости; Dyj>= !((^V){ij} + (^VT)^tj^), (i = Ь,ф,ф; j = Ь,ф,ф) - физические компоненты тензора скоростей деформаций; VV - тензор градиента скоростей; VVT- транспонированный тензор градиента скоростей. В качестве модели турбулентности применялось прямое численное моделирование. Разработанная математическая модель позволила смоделировать сложный гидродинамический процесс теплообмена в змеевике с неизменяющимся радиусом изгиба винтовой трубы (рис. 3). a) b) Рис. 3. Результаты моделирования гидравлического процесса в змеевике для лабораторного стенда: a – кинетическая энергия; b – векторы скорости движения теплоносителя Fig. 3. The results of modeling hydraulic process in a coil for a laboratory stand: a – kinetic energy; b – vectors of the heat carrier velocity По результатам моделирования видно, что при малых значениях числа Дина кривизна трубы еще не оказывает влияние на характер движения теплоносителя – вектора указывают на параллельное движение искривленной оси трубы, в потоке отсутствует поперечная циркуляция, а распределение скорости и закон сопротивления в изогнутых трубах оказывается таким же, как и в прямых. Схемы гидравлической и аэродинамической систем стенда Разработан специальный лабораторный практикум для проектируемого стенда, который, в соответствии с поставленными задачами должен охватывать следующие разделы обучения [13]: - Исследование режимов течения жидкости и воздуха; - Управление насосом и вентилятором; - Исследование работы приборов для измерения скорости движения, объема и температуры воздуха и жидкости в системах. Лабораторная работа № 1 «Исследование режимов течения жидкости в навитом змеевике» включает в себя следующие части моноблока (рис. 4): навитый змеевик, емкость с питательной водой, насос, расходомер, контрольно-измерительная и запорно-регулирующая арматура, шкаф управления. Жидкость (вода) подается в навитый змеевик с помощью насоса из заполненной емкости питательной воды. Контур является замкнутым, вода Рис. 4. Схема гидравлической системы лабораторного стенда:1 – змеевик; 2 – емкость питательной воды; 3 – насос; 4 – расходомер; 5 – датчик давления; 6 – фильтр-грязевик; 7 – обратный клапан; 8 – кран шаровый (слив); 9 – кран шаровый Fig. 4. Diagram of the hydraulic system of the laboratory stand:1 – coil; 2 – feed water tank; 3 – pump; 4 – flow meter; 5 – pressure sensor; 6 – sump filter; 7 – check valve; 8 – ball valve (drain); 9 – ball valve Отберстия для зам ер об скорости и температуры бездушного потока Рис. 5. Схема аэродинамической системы лабораторного стенда:1 – вентилятор; 2 – цилиндр со змеевиком Fig.5. Diagram of the aerodynamic system of the laboratory stand: 1 – fan; 2 – cylinder with coil возвращается в емкость. Измерительная часть стенда позволяет зафиксировать параметры расхода жидкости через табло на расходомере или с последующим выводом показателей на экран ПК при помощи программного обеспечения. Лабораторная работа № 2 «Исследование режимов течения газов (воздуха) в цилиндрическом канале коаксиальной формы» включает в себя следующие части моноблока: металлический цилиндр, навитый змеевик, образующие канал коаксиальной формы, вентилятор, анемометр, запорная арматура, шкаф управления (рис. 5). Подача сжатого воздуха осуществляется через канал в крышке цилиндра. Воздух проходит по каналу и выходит с другой стороны цилиндра через аналогичное отверстие во второй крышке цилиндра. Коаксиальный змеевик внутри цилиндра создает аэродинамическое сопротивление, формируя вихревой воздушный поток. Измерительная часть стенда позволяет измерять параметры скорости и температуры потока воздуха с помощью анемометра путем помещения телескопического зонда в специальные отверстия в цилиндре по движению воздушного потока. Управление анемометром осуществляется с помощью смартфона, с последующей выгрузкой сводных таблиц с экспериментальными значениями на ПК. Управление стендом Управление лабораторным стендом осуществляется посредством управляющего устройства – контроллера. В качестве системы автоматического управления выбрано разомкнутое управление (рис. 6). Для простоты управления и считывания сигналов в системе управляющее устройство получает информацию о цели управления в виде меняющегося во времени задания g(f) и формирует управляющее воздействие на объект таким образом, чтобы достигалась цель управления x(t). Так как выходная величина x не измеряется, то фактическое состояние объекта не контролируется. Алгоритм управления, связывающий управляющее воздействие u(t) с заданием g(f), формируется на основе математической модели объекта, которая известна с высокой точностью [14]. Рис. 6. Функциональная схема системы автоматического управления: yy – управляющее устройство; O – объект управления Fig. 6. Functional diagram of the automatic control system: yy – control device; O – control object Достоинством представленной схемы является простота в эксплуатации и возможность ее дальнейшей модернизации с учетом новых возможностей оборудования. Недостатком является условие, что на объект не должны действовать внешние возмущения, что является трудновыполнимой задачей. Алгоритм работы стенда На рис. 7 представлена блок-схема алгоритма оценки работы стенда [15]. В качестве показателя Рис. 7. Блок-схема алгоритма оценки работы лабораторного стенда Fig. 7. Flowchart of the algorithm for evaluating the work of the laboratory stand Рис. 9. Фото лабораторного стенда Fig. 9. Photograph of the laboratory stand безопасной работы гидравлической системы выбран параметр давления (p, МПа). Аэродинамическая система не нуждается в контроле по давлению, так как скорость потока воздуха от подобранного вентилятора мала (проведено тестирование на этапе сборки), соответственно, воздействия на металлический каркас стенда несущественны. Электрическая схема и подбор оборудования При проектировании электрической схемы (рис. 8) учитывалось, что учебный лабораторный стенд должен включать оборудование, необходимое для ручного управления и с последующей возможностью автоматического управления при помощи программного обеспечения на ПК (персональный компьютер) для создания человекомашинного интерфейса (для визуализации процесса, его управлением, а также отображения, архивирования и протоколирования сообщений от процесса). Управляющим устройством выбран программируемый логический контроллер марки ОВЕН с СoDeSys V2.3 (интегрированная среда разработки (IDE) приложений для программируемых контроллеров). Для измерения расхода подобран электромагнитный преобразователь расхода марки МастерФлоу. В качестве гидравлического устройства выбран Вихревой поверхностный насос фирмы Pedrollo. Для контроля давления подобраны датчики давления ДДМ-1010. Для замера скорости воздуха приобретен анемометр смарт-зонд фирмы TESTO, который отправляет данные на смартфон, а полную информацию можно скачать на ПК. Для автоматического регулирования частоты вращения электродвигателей переменного тока подобрано устройство фирмы МОМЕНТУМ – преобразователь частоты МТ-100 (далее по тексту – ПЧ). Для размещения оборудования спроектирована общая рабочая зона – металлический стол с прикрепленными кронштейнами для моноблока, насоса, шкафа управления, расходомера и другого вспомогательного оборудования. Произведена сборка и наладка лабораторного стенда (рис. 9). Практическая часть Произведены испытания гидравлической системы стенда при разных скоростях двигателя насоса. Регулирование производилось с помощью ПК и контроллера через программу VinCC (рис. 10). Рабочий стол виртуального управления предполагает запуск ПЧ (готовность к работе), задание скорости электродвигателя (обороты в минуту). Текущие значения на виртуальном управлении меняются в реальном времени, но с задержкой в пару секунд. На схеме отображена сигнальная лампа о включении насоса, фиксируются онлайн значения расхода (кубические метры в час) и давления на входе в змеевик (кПа). Запись и сохранение экспериментальных значений осуществляется в журнал в формате Excel на подключенном ПК. Результаты первого эксперимента (выборка без повторяющих значений по скорости от времени) представлены в таблице. При D/d = 25 (для стенда) из расчета по (3) число Reкр = 7139,85, что является значительно Рис. 10. Рабочий стол виртуального управления лабораторным стендом Fig. 10. Virtual control desk of the laboratory stand Результаты эксперимента Results of the experiment Скорость двигателя, об/мин Давление, кПа Расход, м3/ч Число Re 2500,38 531,07 0,902 310 119,5 2354,8 493,966 0,88 292 063,4 2002,16 331,834 0,775 248 325,8 1885 175,057 0,7 233 794,6 1531,2 175,057 0,623 189 913,2 1296,88 72,817 0,623 160 850,7 999,92 71,888 0,52 124 019,0 881,6 71,888 0,314 109 343,9 764,44 54,738 0,314 94 812,7 619,44 54,129 0,313 76 828,5 592,76 54,128 0,262 73 519,4 499,96 28,609 0,262 62 009,5 269,12 6,969 0,047 33 378,7 151,96 3,363 0,024 18 847,4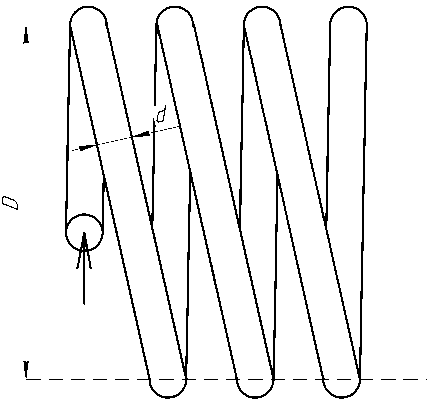
-нф*

Список литературы Опытное исследование аэро- и гидравлической систем прямоточного котла на лабораторном стенде путем внедрения автоматического управления устройствами и сбора данных
- Дудкин М.М., Осинцев К.В., Кускарбекова С.И. Опытное исследование работы парового котла змеевикового типа при эксплуатации на северном нефтяном месторождении // Вестник ЮУрГУ. Серия «Энергетика». 2019. Т. 19, № 4. С. 14-25. DOI: 10.14529/power190402
- Зыков А.К. Паровые и водогрейные котлы: справ. пособие. 2-е изд., перераб. и доп. М.: НПО ОБТ, 1995. 119 с.
- Петухов Б.С. Теплообмен и сопротивление при ламинарном течении жидкости в трубах. М.: Энергия, 1967. 409 с.
- Germano M. The Dean equations extended to a helical pipe flow // Journal of Fluid Mechanics. June 1989. Vol. 203. P. 289-305. DOI: 10.1017/S0022112089001473
- Кириллов П.Л., Юрьев Ю.С., Бобков В.П. Справочник по теплогидравлическим расчетам: ядерные реакторы, теплообменники, парогенераторы / под общ. ред. П.Л. Кириллова. М.: Энергоатомиздат, 1984. 296 с.
- Mori Y., Nakayama W. Study on Forced Convective Heat Transfer in Curved Pipes (1st Report, Laminar Region) // International Journal of Heat and Mass Transfer. 1965. Vol. 8 (1). P. 67-82. DOI: 10.1016/0017-9310(65)90098-0
- Багоутдинова А.Г., Золотоносов Я.Д. Змеевиковые теплообменники и их математическое описание // Известия вузов. Строительство. 2015. № 7. С. 44-52.
- Сопряженная задача теплообмена при течении жидкостей в змеевиках с изменяющимся радиусом изгиба винтовой спирали / Е.К. Вачагина, А.Г. Багоутдинова, Я.Д. Золотоносов, И.А. Князева // Вестник технологического университета. 2015. Т. 18, № 16. С. 234-238.
- Назмеев Ю.Г. Гидродинамика и теплообмен закрученных потоков реологически сложных сред. М.: Энергоиздат, 1966. 368 с.
- Аронов И.З. О гидравлическом подобии при движении жидкости в изогнутых трубах-змеевиках // Известия вузов. Энергетика. 1962. № 4. С. 52-59.
- Zapryanov Z., Christov Ch., Toshev E. Fully developed laminar flow and heat transfer in curved tubes // International Journal of Heat and Mass Transfer. June 1980. Vol. 23, iss. 6. P. 873-880.
- Багоутдинова А.Г., Золотоносов Я.Д. Математическая модель сопряженной задачи теплообмена при турбулентном течении в каналах сложной геометрии // Известия КГАСУ. 2013. № 2 (24). С.157-167.
- Дудкин М.М., Осинцев К.В., Кускарбекова С.И. Разработка методологических основ исследования процессов парообразования при движении многокомпонентной жидкости в прямоточных котлах змеевикового типа методами математического моделирования // Промышленная энергетика. 2020. № 11. С. 16-24. DOI: 10.34831/EP.2020.16.79.003
- Булкин А.Е. Автоматическое регулирование энергоустановок: учеб. пособие. М.: МЭИ, 2016. 508 с.
- Математика и информатика / Е.Н. Гусева, И.Ю. Ефимова, И.И. Боброва, И.Н. Мовчан. 2-е изд. М.: ФЛИНТА, 2015. 197 с.
- Пат. 2694890 Российская Федерация. Электронагреватель жидкости / К.В. Осинцев, В.В. Осинцев, В.И. Богаткин, Е.В. Торопов, С.И. Кускарбекова; заявитель и патентообладатель ФГАОУ ВО «ЮжноУральский государственный университет» (НИУ). № 2018143417; заявл. 06.12.2018; опубл. 18.07.2019. 8 с.


