Орбифолды в одномерных пространствах Кэли-Клейна

Орбифолды лежат на пересечении многих различных областей математики, включая алгебраическую и дифференциальную геометрию, топологию, алгебру. В физике они нашли применение для описания компактификаций дополнительных измерений в теориях Калуцы-Клейна и суперструн [1–3]. В калибровочных теориях орбифолды появляются как фазовое или конфигурационное пространство [4–6].

Идеи многомерия в работах математиков обсуждались уже давно. В конце 1921 г. в Германии опубликована статья Т. Калуцы [7], в которой было предложено объединение электромагнетизма и гравитации в пятимерном пространстве-времени. О. Клейн в работе [8] показал, что дополнительное измерение может быть скомпактифицировано до размеров порядка планковской длины l _Pl ≈ 1 . 6 · 10 ^{- 35} м. Этому соответствует планковская энергия E ∼ 10 ¹⁹ ГэВ. На таких масштабах практическое обнаружение скрытых размерностей выходит за рамки современных экспериментальных возможностей. В дальнейшем было показано, что используя большее число дополнительных измерений, можно единым образом описать все фундаментальные взаимодействия. Сейчас теориями Калуцы-Клейна принято называть целый класс теорий, основанных на предположении о существовании дополнительных компактных пространственных измерений [9–12].

Р. И. Пименов для построения единой полевой теории гравитации и электромагнетизма использовал полурима-нову геометрию ³ V ⁴ ₅ , в которой базой является четырех-

Orbifolds in one-dimensional Cayley-Klein spaces

I. V. Kostyakov, V. V. Kuratov

Institute of Physics and Mathematics,

Federal Research Centre Komi Science Centre, Ural Branch, RAS,

Syktyvkar

Discrete symmetry groups of motions of the elliptic, hyperbolic and Euclidean lines are described. Orbifolds on these lines, obtained by factorization by the corresponding discrete group, are considered. Orbifolds in the form of segments and circles can be used in Kaluza-Klein models and superstring theory for compactification of extra dimensions.

В модели Рэндалл-Сундрума [16] дополнительное измерение представляет собой орбифолд S ¹ / Z ₂ , имеющий вид отрезка с двумя неподвижными точками, в которых расположены две браны, на одной из которых локализованы поля Стандартной модели.

Десятимерная теория суперструн также является серьезным кандидатом на объединение Стандартной модели и квантовой гравитации. Чтобы получить четырехмерную суперсимметричную теорию, нужно скомпактифицировать 6 из 10 измерений на пространства Калаби-Яу. Другой эквивалентный подход, предложенный Д. Гепнером, связан с компактификацией шести дополнительных измерений на N = 2 суперконформную теорию поля с центральным зарядом c = 9 . В работах [17–19] предложены новые конструкции моделей орбифолдов для подхода Гепнера к четырехмерной суперструне.

В данной работе мы опишем одномерные орбифолды в пространствах Кэли-Клейна, которые могут быть использованы при компактификации дополнительных измерений и приведем простые примеры из классической и квантовой механики на этих орбифолдах.

1. Три геометрии Кэли-Клейна на прямой

На прямой имеется три различные геометрии Кэли-Клейна — эллиптическая геометрия Римана, обычная геометрия Евклида и гиперболическая геометрия Лобачевского [14, 15, 20–25], соответственно положительной, нулевой и отрицательной кривизны, которые определяются своими группами симметрий, являющихся подгруппами преобразований проективной прямой. Эллиптической геометрии соответствует группа вращений окружности O (2) , геометрии Евклида — группа трансляций и отражений, гиперболической — группа Лоренца O (1 , 1) .

Моделью для эллиптической прямой (будем обозначать ее как Ell1) можно взять окружность радиуса R с отождествленными противоположными точками на плоскости R2 (рис. 1 a) там же. Примем за расстояние между точками A1 и B1 длину дуги A1B1 (рис. 1 a), пропорциональную углу ϕA1B1 между прямыми OB1 и OA1 и радиусу R окружности sA 1 B 1 = R \фА 1 B 1 | • (1)

Длина всей эллиптической прямой равна πR , поэтому она компактна в метрическом смысле. Две различные точки эллиптической прямой делят ее на две части. Длина одной из них меньше ¹ ₂ πR , другой – больше. Поэтому расстояние между двумя точками двузначно и выбирается меньшее из них.

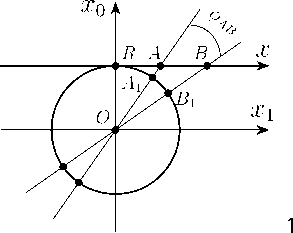
a) эллиптическая прямая

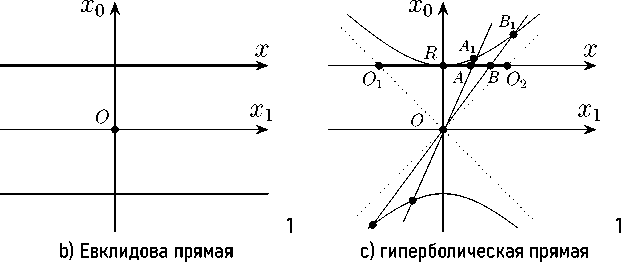
Рисунок 1. Три геометрии Кэли-Клейна на прямой как окружности S ¹ ( j ) /С 2 с отождествленными противоположными точками.

Figure 1. Three Cayley-Klein geometries on the line as circles S ¹ ( j ) /С 2 with identified antipodal points.

Пусть ( x 0 ,x 1 ) — декартовы координаты на плоскости R ² . В полярных координатах связь между углом ϕ и координатами x _i задается формулами

( x ₀ = r cos ф, , n \

S 0 -Г, Ф £ [°, 2п) •(2)

[ x 1 = r sin ф,'

Тогда расстояние s _{A 1 B 1} между точками A ₁ и B ₁ на эллиптической прямой можно определить по формуле

_ n sAiBi       11। cos -R- = R2 |x0A 1x0B 1 + x 1A 1 x 1B 1 | •

Эллиптическую прямую можно рассматривать и как проективную прямую, снабженную расстоянием (1), (3). Действительно, прямые, проходящие через центр и противоположные точки окружности, образуют проективную прямую R P ¹ = S ¹ / Z ₂ , где Z ₂ — группа поворотов на 180 ° , связывающая противоположные точки окружности.

Можно каждой точке эллиптической прямой сопоста- x ₁

вить бельтрамиеву координату x = R —, x = R tg ф . x 0

Тогда расстояние (1) или (3) между точками A и B эллиптической прямой можно выразить через координаты этих точек x _A и x _B

Для близких точек с координатами x и x + dx , расстояние и метрика определяются формулами

d s = R d ф =

d x

^, x ²

⁺ R ²

g = (¹⁺ R)

Множество точек эллиптической прямой, так же как и проективной, можно выбрать по-разному. Действительно, каждому значению бельтрамиевой координаты x соответствует бесконечный набор точек прямой x = R^{x 1} на x 0 плоскости ( x 0 ,x 1 ) . Представим эллиптическую прямую в виде прямой x ₀ = R , к которой добавлена бесконечно удаленная точка (рис. 1 a). Движения одномерного эллиптического пространства, сохраняющие расстояния (1),(4), определяются группой вращения O (2) , которая на координаты x 0 ,x 1 действует вращениями A ( ф ) и отражениями P ( ф )

^s AB ⁼

R arctg

x B - x A

■

A ( ф ) = ( cos ф sin ф

— sin ф cos ф

,

p ( ф ) = (^cos2 ^ф sin 2 ф

sin 2 ф

— cos 2 ф

,

(! 0)=(

cos ф sin ф

(Ю)-(

cos 2 ф sin 2 ф

— sin ф cos ф sin 2ф

— cos 2 ф

^xx ⁰1     ,

)( 1.: ) ■

а на бельтрамиеву координату x — дробно-линейными преобразованиями

‘ x + R tg ф ‘   —x + R tg ф x 1 - Rtgф, x 1 + Rtgф

.

Матрица P ( ф ) задает симметрию (отражение) относительно прямой x 1 = x 0 tg ф . Композиция двух отражений P ( ф 1 + ф ) • P ( ф 1 ) задает вращение A(2ф ) на угол 2 ф . Группы движений эллиптической прямой и окружности (а значит и их геометрии) изоморфны.

Рассмотрим спинорное представление группы движений эллиптической прямой [23,24]. Алгебраический подход связан с сопоставлением вектору X = ( x 0 , x 1 ) t на плоскости R ² с метрикой g _mn = diag(1 , 1) элемента алгебры

Л

Клиффорда X = x0ei + xie2 = zf + zf, z = x + iy, z = x — iy вещественной алгеброй Клиффорда ClR с единичным элементом I и образующими e1 и e2, которые удовлетворяют определяющим соотношениям emen + enem — 2gnmI■ n, m — 1■ 2•     (9)

В матричном виде образующие en можно представить как e 1 =(1 0 )■ e 2 =(“ -У

e ¹ e ² = i ( 0 - °1 ) •

_

Введем новые образующие f и f [26]

^f = 2⁽ e ^{1 + ie 2} ) = ( 0 0 ) ■ f= 2⁽ e ¹ - ^{ie 2} ) = ( 10 ) ■

которые вместе с единицей I образуют одномерную алгеб-руA1 свободного фермиона или фермионного осциллятора f 2 = f2 = 0, ff + ff = I. (12)

Алгебра A1 ввиду (11) изоморфна алгебре Клиффорда Cl2, поэтому построение представлений алгебры Клиффорда можно свести к построению пространства Фока F, соответствующего алгебре фермионного осциллятора (12). Вакуумный вектор 10) и вектор 11), определяемые как f 10) = 0,   |1) = f 10 )■

I0) = ( 0 )■ ID = ( 0 ) ■         <13> задают базис в пространстве Фока. Вектор |ф) = ф010) + ф 111) в этом пространстве называется спинором.

Так как e 2 = 1 , они задают некоторые отражения в R ² . Образующая e 1 задает отражение p 1 = e 1 = f + f относительно прямой x 1 = 0 , ( x 0 ,x 1 ) ч ( x 0, —x 1 )

X ‘ = p i Xp i = x о e i — x i e 2 = zf + zf,   (14)

а отражение относительно прямой x ₀ = 0 , ( x ₀ ,x _i ) ч ( —x ₀ , x _i ) задается элементом p 2 = e 2 = i ( f — f )

X ‘ = p 2 Xp 2 = —x о e i + x i e 2 = — ( zf + zf ) • (15)

Отражению относительно прямой x _i = x ₀ tg ф сопоставляется элемент алгебры Клиффорда p ( ф ) = cos ф e _i + sin ф e ₂ = e -i f + e i f, p ² ( ф ) = 1

X ‘ = p ( ф ) Xp ( ф ) .                (16)

Заметим, что p ( ф ) и —p ( ф ) задают одно и то же отражение. Композиция двух отражений p ( ф _i ) и p ( ф _i + ф ) задает спинорное представление a ( ф ) вращения A (2 ф ) (6) на удвоенный угол 2 ф

a ( ф ) = p ( ф i + ф ) • p ( ф i ) =

= cos( ф ) I — sin( ф ) e i e 2 = e - iff + e i ff, (17)

a - ¹ ( ф ) = (фф ) = p ( ф i ) • p ( ф i + ф ) =

= cos( ф ) I + sin( ф ) e 1 e 2 = e ^iф ff + e -i ff. (18)

X ‘ = a ( ф ) X (( ф ) .                (19)

a ( ф ) и —a ( ф ) задают одно и то же вращение. Формулы (16), (19) задают спинорное представление Pin(2) отражений P ( ф ) и вращений A (2 ф ) (6) группы O (2) элементами алгебры Клиффорда ±p ( ф ) и ±a ( ф ) . Ввиду того, что одному элементу группы O (2) соответствует два элемента спинорного представления, последнее является двойной накрывающей группы O (2) . Действие p ( ф ) и a ( ф ) на спиноры 1ф) = ф ₀ 1 0 ) + ф 1 1 1 ) определяется так

Ю = p ^{( ф} ) if  Wi = a ^{( ф} ) if     ⁽²⁰⁾

Повороту на угол 2 ф в пространстве R ² , задаваемому матрицей A (2 ф ) , соответствует поворот на угол ф в спинорном пространстве, задаваемый матрицей a ( ф ) .

Есть ли в подмножестве алгебры Клиффорда x0e 1 + x 1 e2 = zf + zf, соответствующем плоскости R2, подмножество, остающееся инвариантным относительно действия вращений (19)? Несложно убедиться, что это одномерные подпространства вдоль образующих f и f. Покажем, что они соответствуют изотропным подпространствам в R2 [24,27]. Координаты изотропных векторов 5 = (x0, x 1)t в R2, удовлетворяют соотношению x 0 + x2 = 0.                   (21)

В проективной геометрии эти изотропные подпространства называются абсолютами. Имеем две возможности x0 = £2, x 1 = if 2 и x0 = £2, x 1 = —if2. В бельтрамиевых координатах у эллиптической прямой имеется два абсолюта x = ±iR, которые остаются инвариантными при преобразованиях (8). Этим изотропным векторам соответствуют элементы алгебры Клиффорда

В бельтрамиевых координатах расстояние выражается формулой и спиноры

Ξ 1 = ξ 1² f,  Ξ = ξ 2² f            (22)

s AB = |Rϕ AB | =

R arcth

x B - x A

R (1 - R )

| Ψ 0 ⟩ = ξ 1 | 0 ⟩ ,    | Ψ 1 ⟩ = ξ 2 | 1 ⟩ .            (23)

При преобразованиях (19) и (20)

ˆ

Ξ 1 → e

2 iϕ _ˆ Ξ 1 ,

ˆ

Ξ 2 → e

2 iϕ _{Ξ 2 ,}

Группой симметрии гиперболического пространства, сохраняющей расстояние (29), является группа Лоренца O (1 , 1) , которая в пространстве Минковского действует собственными преобразованиями Лоренца A ( ϕ ) и отражениями P ( ϕ )

| Ψ 0 ⟩ → e ^-iϕ | Ψ 0 ⟩ ,   | Ψ 1 ⟩ → e ^iϕ | Ψ 1 ⟩ .

A(ϕ) =   chϕ sh ϕ

sh ϕ ch ϕ

Таким образом, координаты спиноров связаны с координатами вдоль абсолютов, а спинорные представления вращений эллиптической прямой соответствуют преобразованиям абсолютов при этих движениях.

Аналогично эллиптическому случаю, в качестве модели для одномерного вещественного гиперболического пространства отрицательной кривизны H ¹ (одномерного пространства Лобачевского) можно взять гиперболу (псевдоокружность) (рис. 1 c)

ch ϕ sh ϕ

^{P ( ϕ ) =}    - sh ϕ - ch ϕ ^,

^xx ′ 01     =

^xx ′ 01     =

ch ϕ sh sh ϕ ch

ϕ     x 0

ϕ     x 1

ch ϕ sh ϕ - sh ϕ - ch ϕ

-

x 0

x 1

,

) ■

а на бельтрамиеву координату следующими дробно-ли-

нейными преобразованиями

x ₀ - x ² ₁ = R ²                 (25)

_′ x + R th ϕ _′ x + R th ϕ x = _x , x = - _x .    (32)

с отождествленными противоположными точками двух ее веток в пространстве Минковского R1,1 с метрикой ds2 = dx20 - dx21.                 (26)

Множество прямых, проходящих через центр и пару противоположных точек ветвей гиперболы, лежат между изотропными прямыми x ₀ = ±x ₁ , которые соответствуют абсолютам в проективной геометрии. Каждой такой прямой можно сопоставить точку одномерного гиперболиче- x ₁ ского пространства, бельтрамиеву координату x = R x 0

и гиперболический угол ϕ. В полярных координатах связь между гиперболическим углом ϕ и координатами xi задается формулами xx01== rr schh ϕϕ,, , ϕ ∈ (-∞, +∞). (27)

Выберем в качестве множества таких точек интервал ( O ₁ , O ₂ ) на прямой x ₀ = R , где точки O _i соответствуют изотропным прямым (абсолютам) x ₀ = ±x ₁ (пунктирные линии на рис. 1 c), x _{O 1} = -R , x _{O 2} = R . В релятивистской механике эти изотропные прямые (абсолюты) связаны со световыми конусами и движением частиц нулевой массы (например, фотонами), при этом само пространство Лобачевского является пространством скоростей и имеет тесную связь со специальной теорией относительности [28].

Расстояние между точками A ₁ и B ₁ на гиперболе (псевдоокружности) (рис. 1 c) (с учетом (26),(27)) пропорционально гиперболическому углу ϕ A ₁ B ₁ = ϕ A ₁ - ϕ B ₁

s A 1 B 1 = R|ϕ A 1 B 1 |. (28)

Если обозначить v1 = Rthϕ1, v2 = Rthϕ2, то композиция двух преобразований, задаваемых векторами v1 и v2, будет задаваться вектором v v1 + v2 v1v2 .

1+ _{R 2}

Заменяя R на скорость света, c легко увидеть формулу сложения скоростей в специальной теории относительности (СТО) и то, что скорость света является предельной (абсолютом). Абсолюты O 1 и O 2 остаются инвариантными при действии группы O (1 , 1) . Расстояние между точками A и B можно определить, как в проективной геометрии, с помощью двойного отношения

_ 1 pi ( AO 1 1 Ibo 2 1 A _

^AB 2 R l G AO 2 1 IBO i l)

= 1R ln ( ⁽ R ⁺ x A ) ■ R-x B ) ) ■ (34) ²      \⁽ R ^- x A ) ⁽ R + x B )/

Из формулы (34) видно, что расстояние от любой точки гиперболической прямой до абсолюта равно бесконечности, поэтому гиперболическая прямая некомпактна в метрическом смысле. Легко показать, используя связь гиперболического логарифма и гиперболического арктангенса, что формулы (34) и (29) эквивалентны. Кэли для определения расстояний использовал арккосинусы, а Клейн — логарифмы. Для близких точек с координатами x и x+dx формулы (29) и (34) дают расстояние и метрику dx                x2 -2

d s = _{1 - R x} 2 ₂ , g = 1 - _{R 2}      .      (35)

Таким образом, гиперболическая прямая (прямая Лобачевского) изображается отрезком ( O 1 O 2 ) (модель Кэли-Клейна) с расстоянием, определяемым формулами (34) и (35). При замене R на iR , геометрия Лобачевского переходит в эллиптическую. Так как с проективной точки зрения эллиптическая прямая тоже имеет два мнимых абсолюта x 0 = ±ix 1 или x = ±iR , инвариантные относительно вращений (7), (8), на ней можно определить расстояние, эквивалентное (4)

S AB =- R lj ( i^{R +} x A ) • ( i^R — x B ) V   (36)

2      \( iR — x a ) ( iR + x b ))

Рассмотрим спинорное представление группы движений гиперболической прямой [23, 24]. Вектору XX = ( x 0 ,x 1 ) t пространства Минковского R ¹ ’ ¹ с метрикой g mn = diag(+1 , — 1) сопоставим элемент X = x 0 e 1 + x 1 e 2 = z ₊ f + z - f , z ± = x ± У вещественной алгебры Клиффорда Cl ₍ ^R _{1 , 1)} с единицей I и образующими e ₁ и e ₂

e m e n + e n e m = 2 g nm I, n,m = 1 , 2 .    (37)

В матричном виде образующие en равны e 1 =(1 J)- e 2 =( —“I 0 ), e 1 e 2 = ( -1 1) - f = 2(e 1 + e2)= ( 0 0 ) - f"=|(e 1 — e2) = ( 10 ) .

Отражение относительно прямой x 1 = th фx0 задается двумя элементами алгебры Клиффорда p(ф) = e 1 ch ф + e 2 sh ф = ef + e -f и - p (ф), p2 (ф) = 1, действующими по формуле л              л

X ‘ = p ( ф ) X p ( ф ) .

Композиция двух отражений p(ф 1) и p(ф 1+ф) задает спинорное преобразование Лоренца a(ф), соответствующее преобразованию Лоренца A(2ф) (30) на удвоенный угол 2ф a (ф) = p (ф 1 + ф) • p (ф 1) =

= ch( ф ) I — sh( ф ) e 1 e 2 = e ff + e - ff. (41)

a 1 ( ф ) = p ( ф 1 ) • p ( ф 1 + ф ) =

= ch( ф ) I + sh( ф ) e 1 e 2 = e ~^ ff + e f f. (42)

X ‘ = a ( ф ) X a ^- 1 ( ф ) .              (43)

a ( ф ) и —a ( ф ) задают одно и то же вращение. Формулы (40), (43) задают спинорное представление Pin(1 , 1) отражений P ( ф ) и вращений A (2 ф ) (6) группы O (1 , 1) элементами алгебры Клиффорда ±p ( ф ) и ±a ( ф ) . Это представление является двойной накрывающей группы O (1 , 1) . Действие на спиноры описывается формулой (20).

Повороту на гиперболический угол 2ф в пространстве R1 ’ 1, задаваемому матрицей A(2ф), соответствует поворот на угол ϕ в спинорном пространстве, задаваемый матрицей a(ф). Точно так же, как в эллиптическом случае, несложно убедиться, что одномерные подпространства вдоль f и f соответствуют изотропным подпространствам в R1,1 [24,27]. Координаты изотропных векторов 5 = (x0,x 1)t в этом случае удовлетворяют соотношению x20 — x21 = 0.                  (44)

Имеем две возможности x 0 = £ 2 , x 1 = £ 2 и x 0 = € 2 , x 1 = ^{— £} 2 . В бельтрамиевых координатах на гиперболической прямой им соответствуют два абсолюта x = ±R , которые остаются инвариантными при преобразованиях (32). Этим изотропным векторам соответствуют элементы алгебры Клиффорда

51 = £ 2 f,  5 2 = £ 22 f и спиноры

I Ф о ) = £ 1 1 0 j, | Ф 1 ) = £ 2 1 1 j.

При преобразованиях (43) и (20)

5 1 ^ e ² ^ 5 1 , 5 2 ^ e ^{- 2} ^ 5 2 , I Ф о )^ e * | Ф о j,   I Ф 1 )^ e ' Ф 1 j.

Таким образом, как и для эллиптической прямой, координаты спиноров связаны с координатами вдоль абсолютов, а спинорные представления преобразований Лоренца гиперболической прямой соответствуют преобразованиям абсолютов при этих движениях.

Евклидову геометрию можно получить из эллиптической или гиперболической в пределе больших R , при этом два абсолюта сливаются в один (бесконечно удаленная точка), и расстояние определяется обычным образом как разность координат

S AB = |x a — x b I,     d s = d x. (48)

Топологически, одномерная евклидова прямая эквивалентна эллиптической прямой, из которой выколота одна точка. И наоборот, если к евклидовой прямой добавим бесконечно удаленную точку, то получим эллиптическую прямую (окружность).

Также группу трансляций и отражений на евклидовой прямой можно представить с помощью вырожденной алгебры Клиффорда Cl ₍ ^R _{1 , 0 , 1)} . Для этого рассмотрим полуев-клидово пространство с метрикой g = diag(1 , 0) и каждому вектору X = ( x 0 , x 1 ) t этого пространства сопоставим элемент X = x 0 e 1 + x 1 e ₂ = z ₊ f + z - f , z ± = x ± iy вещественной вырожденной алгебры Клиффорда Cl ₍ ^R _{1 , 0 , 1)} с единицей I и образующими e ₁ и e ₂

^e m ^e n ^{+ e} n ^e m = ² g nm I^{- n,}m = ¹ , ² . ⁽⁴9)

Здесь i - нильпотентная единица со свойством i = 0, но i2 = 0. В матричном виде образующие en равны

(29), (35), (48), с помощью параметра j

e 1 =(1 0) ^,

^e 2 ⁼

ι

( ⁰ -0iy

R  jsAB tg^ jR

x B - x A

1 0

^{e 1 e 2     li} I 0 _- 1 у ^,

d s =

x A x B ^,

^{R 11} - ^{j 2} -R-)

где f и f имеют вид (11), (39). Евклидовой прямой сопоставим слой x 0 = 1 в полуевклидовом пространстве. Тогда каждой точке евклидовой прямой с координатой x можно сопоставить элемент алгебры Клиффорда X = e ₁ + xe 2 . Отражение относительно точки с координатой x = b задается двумя элементами алгебры Клиффорда p ( b ) = ^e i + be 2 и - p ( b ) , p ² ( ф ) = 1

d x

^, x ²

^{+ j} R ²

g =(^{1+ j 2} R)

Также возможно единым образом представить группы движений этих трех геометрий, используя алгебры Клиффорда, связанные с метрикой g = diag(1 ,j ² ) .

2. Орбифолды на одномерных геометриях Кэли-Клейна

X ‘ = p ( b ) Xp ( b ) , x ‘ = 2 b - x. (51)

Композиция двух отражений p ( b ₁ ) и p ( b ₁ + b ) задает трансляцию a ( b ) , соответствующую трансляции на евклидовой прямой на 2 b

a ( b ) = p ( b ₁ + b ) • p ( b ) = I — 2 be ₁ e 2 ,      (52)

X ‘ = a ( b ) X a ^{- 1} ( b ) .               (53)

a ( b ) и —a ( b ) задают одну и ту же трансляцию.

Мы видим, что три одномерные геометрии Кэли-Клейна тесно связаны между собой предельными переходами и аналитическими продолжениями. Они могут быть описаны единым образом [15] как окружности S ¹ ( j ) (рис. 1)

Орбифолд — это многообразие с особенностями и его можно определить как факторизацию многообразия X по некоторой дискретной подгруппе Г группы движений этого многообразия X/ Г . При этом особыми точками будут неподвижные точки этой дискретной подгруппы. Вне особых точек орбифолды устроены так же, как исходное многообразие. Таким образом, чтобы описать орбифолды на одномерных геометриях Кэли-Клейна, нужно описать дискретные подгруппы их групп движений. Начнем с евклидовой прямой. Любая дискретная подгруппа Г группы движений евклидовой прямой имеет вид [29–31]

1. Г порождается одной симметрией (отражением)

Г = D 1 = Z 2 = {e,P ( a,i ) }.

x 0 + j ² x 1 = R ²                (54)

с отождествленными противоположными точками на плоскостях R2(j) = (x0,jx 1) с метрикой ds 2 = d x 0 + j 2d x 1, j = 1 ,i,i,   i2 = 0.    (55)

Значению j = 1 соответствует эллиптическая геометрия, j = i — геометрия Евклида, а j = i — гиперболическая. Группы симметрии G этих окружностей, сохраняющие расстояния (55), состоят из вращений A ( ф,j ) и отражений P ( ф,j )

В матричном виде имеет представление

D 1 ={(0 0) , ( a  -1 )} ■    ⁽⁵⁹⁾

2. Г порождается параллельным переносом T ( a ) = O ( a, i ) , действующим на координату x как

T ( a ) x = x + a, Г = {T ( na ) |n G Z }.

В матричном представлении состоит из бесконечного числа матриц вида

^T -{ (,1 a ⁰ У n ^G Z}

A ( ф, j ) = ( “°⁸ ■

^,J/ у ¹ sin jф

P ( ф,j ) = ( “^{s j}t ^,J/    у j sin jф

-j sin jф cos jф

,

j sin jф — cos jф

.

Как обычно, композиция двух отражений, задаваемых двумя прямыми, относительно которых происходит отражение, дает поворот на угол, равный удвоенному углу между этими прямыми

и изоморфна группе целых чисел по сложению ( Z , +) .

3. Г порождается двумя отражениями P ( a, i ) и P ( b, i ) , действие которых определяется так P ( a, i ) x = a — x, P ( a, i ) ² = 1 , или, так как композиция двух отражений есть трансляция, можно представить подгруппу Г как порожденную параллельным переносом T ( b — a ) и симметрией (отражением) P ( a, i ) ,

Г = {T ( n ( b — a )) , P ( a, i ) T ( n ( b — a )) } = D ^ .

В матричном виде группа диэдра D _∞ представляется бесконечным набором матриц вида

P ( ф 1 + ф,J ) P ( ф 1 ,j ) = A ( ф,j ) .       (57)

D ∞

= Я J П n ( b — a ) 1     ^,

Можно единым образом определить расстояние и метрику на этих трех геометриях, объединяя формулы (4), (5),

¹ n ( b — a )

+ a

-

,

n ∈ Z

.

На рис. 2 приведены примеры орнаментов с группой симметрий D ∞ (2 a) и группой трансляций T (2 b).

Дискретные подгруппы группы движений гиперболической прямой включают в себя подгруппу диэдра D 1 , по-

2a)                     2b)

Рисунок 2. Орнаменты на евклидовой прямой с симметриями D ∞ и T . Figure 2. Ornaments on the Euclidean line with symmetries D ∞ and T .

Дискретные подгруппы группы движений окружности O (2) изучал еще Леонардо до Винчи и дал полный их перечень [32]. Это группы симметрии правильных n -угольников — циклическая группа C _n , порожденная вращением на угол ² _n ^π и состоящая из n поворотов

рождаемую одним отражением

{( 1 0 ) ( ch ф - sh ф )}

D ¹ = Ц 0 1 )' ^sh ф - ch ф J/ ’   ⁽⁶³⁾

C n =

2πk cos2nn ,k= = 0 ,...,П - 1|

дискретную подгруппу Лоренца, порождаемую конкретным бустом (псевдовращением) на угол ϕ , изоморфную группе трансляций (60) или группе целых чисел по сложению ( Z , +) и состоящую из бесконечного числа матриц вида

L ( ф ) = {( ^ch ^Пф ^sh ”1 ) -n € z} - (64) ' 1 \ sh пф ch пф I I

и группа диэдра D _n , порожденная одним (для n = 1 ) или двумя отражениями P ( ф, 1) и P (ф + П , 1) и состоящая из n поворотов на углы ^{2 π} _n ^k и n отражений

Также имеется подгруппа, порожденная двумя отражениями, например, P ( ф, i ) , P ( ф + ф, i )

_ ) ( ch пф sh пф \ “ |P sh пф ch пф j '

D n

IV cos 2nk

Ц sin ²n^k

- sin ^п \

n cos2пк  Г

n

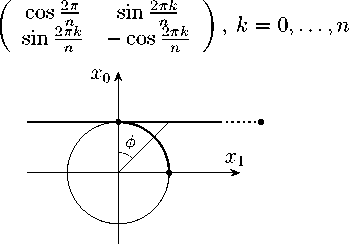
3 a) Эллиптическая прямая

- 1} -

x 0

ch пф

- sh пф

"h ф Y п € z)

- ch пф

и изоморфная бесконечной группе диэдра D ∞ .

x 1

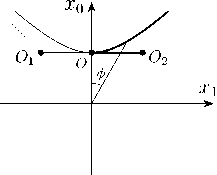
3 c) Гиперболическая прямая

3 b) Евклидова прямая

Рисунок 3. Орбифолды на одномерных геометриях Кэли-Клейна, получаемые факторизацией по подгруппе диэдра D 1 , связанной с отражением.

Figure 3. Orbifolds on one-dimensional Cayley-Klein geometries obtained by factorization by the dihedral subgroup D 1 , related to reflection.

Выбирая в качестве конечной подгруппы группы движений Кэли-Клейна подгруппу диэдра D1, порожденную отражением P(ф-j) относительно соответствующей точки прямой, получаем орбифолды S1(j)/D 1, выделенные на рис. 3 (выбрана точка O(0,0), относительно которой производится отражение, т. е. x → -x). На рис. 3 также отмечены сингулярные точки (неподвижные точки при таком отождествлении). У орбифолда на эллиптической прямой две сингулярный точки, которые делят ее на два равных отрезка длиной 12πR, поэтому он компактный в метриче- ском смысле. Этот орбифолд играет важную роль в теориях суперструн, пятимерных калибровочных теориях Янга-Миллса, моделях Рэндалл-Сундрума и т. д. У орбифолдов на евклидовой и гиперболической прямой — одна сингулярная точка. Орбифолд на евклидовой прямой представляет собой полубесконечный интервал [0, оо], а орбифолд на гиперболической прямой представляет собой отрезок OO2, компактный в топологическом смысле и не компактный в метрическом, так как расстояние от любой точки этого орбифолда до абсолюта O2 равно бесконечности.

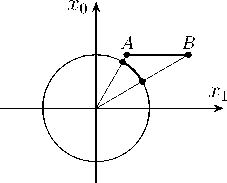
4a) Эллиптическая прямая

A

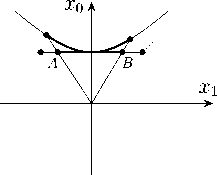
4c) Гиперболическая прямая

4b) Евклидова прямая

Рисунок 4. Орбифолды на одномерных геометриях Кэли-Клейна, получаемые факторизацией по соответствующей дискретной подгруппе диэдра и имеющие вид отрезка AB .

Figure 4. Orbifolds on one-dimensional Cayley-Klein geometries obtained by factorization by the corresponding discrete dihedral subgroup and having the form of a segment AB .

Можно выбрать в качестве дискретной подгруппы, подгруппу, порожденную двумя отражениями P ( ф 1 ,j ) и P ( ф 2 ,j ) . Соответствующие орбифолды в виде отрезков [ AB ] представлены на рис. 4 и имеют две особые точки, соответствующие точкам, относительно которых производятся отражения и которые остаются неподвижными.

Орбифолдами R1 /Т(a) на евклидовой прямой, S1 /Cn на окружности (эллиптической прямой) и H1 /L(ф), на гиперболической прямой являются окружности — компактные многообразия без особенностей, так как дискретные подгруппы трансляций Т(a), вращений Cn и псевдовращений L(ф) на R1, S1 и H1 действуют свободно и не имеют неподвижных точек. Таким образом, орбифолды в одномерных геометриях Кэли-Клейна имеют вид либо отрез- ков с двумя сингулярными точками, либо окружностей, либо полубесконечной прямой с одной особой точкой.

• 3.    Классическая механика свободной частицы на орбифолдах одномерных геометрий Кэли-Клейна

Пространства постоянной кривизны используются в различных областях современной физики. Мы рассмотрим движение свободной частицы в конфигурационном пространстве, являющимся орбифолдом в соответствующем пространстве Кэли-Клейна и которое имеет вид отрезка [ AB ] (рис. 4) и построим орбифолды соответствующих фазовых пространств.

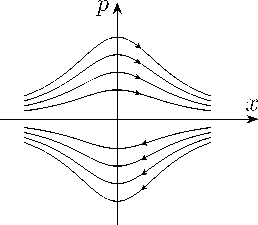
a) Эллиптическая прямая

p

x

c) Гиперболическая прямая

b) Евклидова прямая

Рисунок 5. Траектории свободной частицы p ² = 2 mEg в фазовых пространствах трех одномерных геометрий Кэли-Клейна.

Figure 5. Trajectories of a free particle p ² = 2 mEg in phase spaces of three one-dimensional Cayley-Klein geometries.

a) Эллиптическая прямая

p

AB

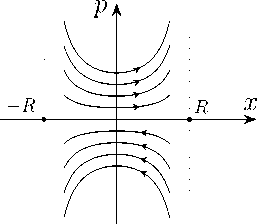
ab

x

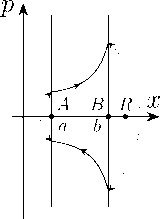
c) Гиперболическая прямая

b) Евклидова прямая

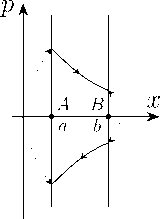
Рисунок 6. Траектории в фазовых пространствах на орбифолдах рис. 4. Пунктирными линиями со стрелками соединены склеиваемые точки.

Figure 6. Trajectories in phase spaces on orbifolds in Fig. 4. The dotted lines with arrows connect the glued points.

Лагранжиан и гамильтониан свободной частицы на всей прямой в трех геометриях можно описать единым образом

• ¹                      P ²

4. Квантовая механика в пространстве-времени с дополнительным измерением

L = ^ —g:x ² , H = g 2— , p = mgx,    (66)

где метрика g для трех геометрий равна g=(1+j 2 R2) -2

Траектории на фазовых плоскостях, соответствующие постоянной энергии E и имеющие вид p ² = 2 —Eg представлены на рис. 5.

Рассмотрим теперь движение в конфигурационном пространстве, которое имеет вид отрезка [AB] и являет- ся орбифолдом, представленным на рис. 4. Фазовое пространство на первый взгляд имеет вид бесконечной полосы, ограниченной двумя прямыми x = а и x = b. Примеры траекторий на этой полосе для всех трех геометрий указаны на рис. 6. В точке (b,p) в результате отражения от точки B импульс меняется на противоположный и траектория в фазовом пространстве меняется скачком на (b, —p). Однако из физических соображений никаких скачков в фазовом пространстве в данной системе быть не может [5, 6]. Нужно отождествить (склеить) точки (b,p) и (b, —p). Это означает, что состояния (b,p) и (b, —p) физически эквивалентны. Также нужно отождествить (склеить) точки (a,p) и (a, —p). В результате получаем орбифолд, имеющий две особые точки (а, 0) и (b, 0), окрестности которых имеют вид конуса.

Площадь под траекториями в фазовом пространстве равна действию S . В классической механике величина этой площади может быть любой. В квантовой механике траектории в фазовом пространстве, представленные на рис. 6, образуют дискретное множество (квантованы) [33]. Разность площадей равна кванту действия h .

Согласно постулату Бора, классическое действие за период равно целому числу квантов [33]

Гамильтониан для одномерного кулоновского на эллиптической прямой

H     ~ ² ( x ² ) d (     x ² ) d

2 m \ RR² J d x \ RR² J d x

Уровни энергии

E n =

~ ² n ²

2 mR ²

-

потенциала

-

q ² |x|^.

^ pdx = nh, n = 1 , 2 ,. ...          (67)

Здесь p и x — это канонически сопряженные импульс и координата. Интеграл (67) равен площади фазового пространства ( p, x ) , ограниченного траекторией движения за период (рис. 6). Траектории на рис. 6 имеют вид p ² = 2 mEg . Подставляя выражение для импульса в формулу (67), получаем, что площадь фазового пространства, задаваемая этой траекторией, и энергия квантованы

b

^ pdx = 2 д/2 mE n J /gd-

!x = 2 nn ~ ,

a

E n =

2 п 2 ~ 2 n ² ml ²

b

, n            2R f , jx\ l = 2 gddx = — I arctg R I

a

b

a

Здесь l — удвоенная длина отрезка [ a, b ] , которая в каждой из трех геометрий считается с учетом метрики g . В классическом случае на величину интеграла (67) не накладывается никаких ограничений и площадь фазового пространства, момент импульса и энергия могут быть любыми. Задача на орбифолдах рис. 4 похожа на обычную задачу квантовой механики на отрезках с двумя бесконечными стенками на концах, где для каждой из трех геометрий учитывается своя метрика.

В работе [34] были исследованы квантовомеханические задачи о гармоническом осцилляторе и кулоновской частице на одномерных геометриях Кэли-Клейна. Уравнение Шредингера в этих примерах имеет стандартный вид

Л

Нф = Бф.

Для осциллятора на эллиптической прямой гамильтониан H с учетом метрики g равен

~ ²/ x ²\ d /     x ²\ d 1

H = -2m d ⁺ R) d x V⁺ R) d x + 2 x

Энергия осциллятора квантуется

E n =     G2 ⁺ n ⁺ 1) ⁺

2 mR ²          2

⁺ h^ ( n ⁺ 2-) У^{1 +}₄ m 2 ^ 2 R,n = 0 , ¹ ,.... ⁽⁷¹⁾

2h 2 n 2 ’ n =1 ’ ² ’...

.

При малых значениях R спектр энергий осциллятора и

од-

номерного атома водорода совпадает со спектром свободной частицы на окружности

E     h ² n ²

n   2 mR¹²

2 п ² h ² n ²

ml ²

, l = 2 nR     (74)

и уходит в область высоких энергий. Таким образом, квантование свободной частицы в случае малых размеров характерных траекторий вполне может служить для оценки спектра энергий.

Рассмотрим уравнение Шредингера для свободной частицы на орбифолдах в виде отрезков рис. 4. Гамильтониан для трех геометрий, используя параметр j , можно записать как

/4

H =

— F (1+ J 2 x ) r(1+ J 2 x ) Г . (75) 2 m       R ² d x       R ² d x

Для евклидовой прямой ( J = i , R ^ ж ) он имеет очень простой вид и общее решение ищем в виде

ф ( x ) = A e ^ikx + B e

-ikx _.

Волновая функция ф(x) при отражениях относительно точек xA = а и xB = b может приобретать дополнительную фазу. Поэтому она должна удовлетворять следующим условиям ф (x ) = e iaф (2 а — x), ф (x ) = eie ф (2 b — x). (77)

Чтобы выполнялось (77), фазы α, β и волновое число k должны быть следующими a = nni, в = nn2, kn = ^n-, n,ni ,n2 G Z. (78) b-a

Тогда волновая функция может быть представлена в виде суперпозиции двух базисных решений

ψ 1 ,n

nn ( x —

= sin —----

b-a

a )                 nn ( x — a ) , ,

—, ф 2 ,n = cos — b———, (79)

а энергия квантуется так же, как и при использовании постулата Бора (68) или (74), где удвоенная длина орбифолда l = 2(b — a). Для эллиптической и гиперболической прямых, переходя от координаты x к угловой ϕ, x = R tg jф, j можно все свести к предыдущим вычислениям и получить такое же выражение для уровней энергии (68),(74), где удвоенная длина l будет вычисляться с учетом метрики на этих прямых, как в (69).

Если мы рассмотрим частицу в некотором пятимерном пространстве-времени, где (3+1) обычные измерения с координатами ( x 0 ,x 1 ,x ₂ , x 3 ) , а дополнительное измерение

с координатой x 5 скомпактифицированно или на окружность или на орбифолд с длиной l (за период) в одной из трех геометрий Кэли-Клейна. Если при этом потенциал зависит только от первых трех координат U ( x 1 ,x 2 ,x 3 ) , то спектр такой системы будет иметь вид

В комплексной записи

L —

1 d^d , Л

—   —+ ia

2 \dt J

z

-

V ( izl 2 ) —

E N,n — E N + , N,n — 0 , 1 ,... . (8⁰⁾ ml ²

Уровни энергии E _N совпадают с уровнями энергии в потенциале U ( x 1 ,x 2 ,x 3 ) и определяются набором квантовых чисел N . При низких энергиях наличие дополнительного измерения не обнаруживается. И только при высоких энергиях E ∼ ^{2 π} _m ² _l ^~ ₂ ² появляются дополнительные уровни, указывающие на наличие дополнительного измерения [1].

Таким образом, планковские кванты энергии могут служить индикатором наличия дополнительного пятого измерения, поскольку связаны с движением частиц по замкнутым траекториям этого измерения.

— 2 r ² + 2 r 2 ( Ф + a) — V ( r 2 ) . (86)

Вращения порождают дополнительные силы инерции — центробежную силу, переносное вращательное ускорение и силу Кориолиса [35].

Мы хотим ввести в лагранжиан (82),(83) компенсирующее (калибровочное) поле A (нулевую компоненту вектор-потенциала A µ в абелевой скалярной электродинамике) так, чтобы компенсировать возникающие при переходе во вращающуюся систему координат силы инерции

L — 2 ( x 1 + Ax 2 ) 2 + 2 ( x 2 — Ax 1 ) ² — V ( r ² ) , (87) или в комплексной записи

L —

5. Модели на двумерных орбифолдах

¹ d-—iA

2 \dt J

z

-

V ( izl ² ) —

Приведем пример естественного возникновения орби-фолда как фазового пространства в SO (2) калибровочной теории в пространстве-времени (0+1) [5, 6]. Рассмотрим простейший пример абелевой калибровочной теории — скалярную электродинамику в пространстве-времени ( 0 + 1 ) [5,6]. Лагранжиан, инвариантный относительно глобальной SO (2) симметрии во внутреннем пространстве полей ( ϕ 1 , ϕ 2 ), имеет вид

L ^— ^ ^ф 1 ⁺ ^ ^ф 2 - V ⁽ Ф 1 ⁺ Ф ^{2 )} ■        ⁽⁸¹⁾

Если заменить обозначения ϕ _i на x _i видно, что лагранжиан (81) описывает нерелятивистскую частицу единичной массы в двумерном пространстве ( x 1 , x 2 )

L ^— 2 x I ⁺ | x 2 - V ⁽ x ^{2 +} x 2 ) .       ⁽⁸²⁾

Удобно ввести комплексную переменную z — x 1 + ix 2 — reiф, с которой лагранжиан (82) примет вид

L — 2 iz1 ² - V ( z 2 ) — 2 r ² + 2 r ² ф ² - V ( r 2 ). (83)

Если мы перейдем во вращающуюся систему отсчета ( x 1 ,x 2 ), z' — e ^ia(t ) z,

^— 2 r ^{2 +} 2 r ^{2 (} ф — A ^{) 2} — V ⁽ r ^{2 )} .

Лагранжиан (87), (88) инвариантен при переходе во вращательную систему координат. Калибровочные преобразования при этом имеют вид

z ' — z e ^{ia (} t ) ,   A ' — A + a ( t ) .         (89)

Поле A в этом случае имеет размерность угловой скорости и порождает те же поля инерции. Действительно, уравнения Эйлера-Лагранжа для поля A лагранжиана (87) имеют

вид

_ x 2 x 1 — x 1 x 2

~2 1 „2

x ₁ + x ₂

Мы можем связать с калибровочными полями A замкнутые 1-формы в качестве связностей

A 1

x 1 d x ₂ — x ₂ d x 1         x 1 d x 1 + x ₂ d x ₂

-2 , „,2 , A ^{2 —} Z2TT2 x ₁ + x ₂                x ₁ + x ₂

iA , + A 2 — d z.

z

^xx ' ¹2    —

cos a ( t ) sin a ( t ) — sin a ( t ) cos a ( t )

^x _x ¹₂     , (84)

Первая 1-форма A 1 соответствует полю, компенсирующему силу, связанную с вращательным ускорением. Вторая A 2 соответствует полю, которое компенсирует центробежную силу.

Гамильтониан этой модели равен

H — 2( p 1 + p 2 )+ A ( p 2 x 1 — p 1 x 2 ) + V ( x 1 + x 2 ) , (92)

то скорость и ускорение будут иметь вид

z:' — (z + iaz) eia (t), z' — (z — a2z + i(az + 2az)) eia(t),

а лагранжиан в декартовых переменных

L — 2 ( x 1 — 'ax 2 ) + 2 ( x 2 + ' ax 1 ) - V ( x 1 + x 2 ) .

где обобщенные импульсы

∂L               ∂L p 1    ...     x 1 + Ax2, p2      .     x2 — Ax 1, (93)

∂x 1                    ∂x 2

n — dL — 0 .

∂A

Имеются две связи первого рода

n — 0 ,     p 2 x 1 — p 1 x 2 — 0 .          (94)

Из трех степеней свободы A, x 1 , x 2 лишь одна физическая. В силу калибровочной инвариантности точки окружности x 1 + x 2 = R ² физически неразличимы. Из уравнения связи (94) следует, что p i = Xx i . Можно положить x 2 = p 2 = 0 и считать, что в фазовом пространстве ( x 1 ,p i ) действует калибровочная группа Z ₂ : ( x i ,p i ) ч ( —x ₁ , —p ₁ ) , при этом точки ( x ₁ ,p ₁ ) и ( —x ₁ , —p ₁ ) физически неразличимы. Физическое фазовое пространство при этом есть конус (орбифолд R ² ( x ₁ ,p ₁ ) / Z ₂ ) [5,6]. Группа Z ₂ является конечной подгруппой калибровочной группы SO (2) .

• 6.    Заключение

Орбифолды на одномерных геометриях Кэли-Клейна имеют вид отрезков, окружностей и полупрямых с соответствующей метрикой. Одномерные орбифолды S ¹ / Z ₂ в виде отрезка с двумя неподвижными точками находят широкое применение в теоретической физике в моделях Ка-луцы-Клейна, Рэндалла-Сундрума, теориях суперструн и других. В работе [36] разбирался пример, связанный с решением Шварцшильда, имеющий вид двух листов, соединенных мостом. Частица представлялась как мост, соединяющий эти листы. Мост можно представить себе и как ор-бифолд.

Орбифолды в виде отрезка на эллиптической и евклидовой прямых эквивалентны и обладают евклидовой метрикой. Интересна возможность применения орбифолда на гиперболической прямой с метрикой геометрии Лобачевского. Мы привели простейшие примеры из классической и квантовой механики на таких орбифолдах.