Orbital ordering probed by electron-spin resonance method in magnetic semiconductors

The electron-spin resonance (ESR) canbeusedto detect orbital-ordering (OO) and to monitor the evolution of the OO parameter. Probing the spin of the non-integer filled d shell of Mn^{(2 + δ )} ions by ESR, the anisotropy and temperature dependence of g -value and linewidth Δ H provide clear information on orbital order via spin-orbit coupling. Promising materials are Co _x Mn_{1– x} S solid solutions, which assume orbital ordering [1–3]. The Co _x Mn_{1– x} S solid solutions can be attributed to the multiferroic class. In the temperature ranges of T ~ (110…120) K and T ~ (230…260) K, the correlation between the magnetic and electric subsystems has been found [3]. The presence of this correlation is confirmed by the magnetic field dependence of the temperature variation of the permittivity having maximum at these temperatures. The first maximum in the low-temperature range is caused by the change in the orbital ordering for cobalt ions surrounded with manganese ions; the second maximum is related to the orbital order in the manganese system.

The reduced ordered moment μ₀ = 4.4μ_B in the AF structure of MnS may be the result of change of manganese ionvalencyMn^{2± δ} orrepartition of electron density between e_g - and t _{2 g} -orbitals. In any case the number of t _{2 g} the orbital occupancy is not equal to n_tg = 3. The uniform orbital occupancy at every site is formed at some high temperature. The MnS₆ octahedra distortion is small and essentially undetectable in X-ray experiments on MnS. The crystal field acting on the Mn^{2± δ} ion is therefore nearly cubic, and heuristically one expects unquenched orbital moment. The spin dynamics of MnS are highly sensitive to the orbital occupancy and can provide important information in this regard.

The aim of the study is to bring to light on mechanism of origin of the correlation between the magnetic and elastic subsystems [3; 4], to establish the role of orbital fiuctuations on the dynamical properties Co _x Mn_{1– x} S sulfides in the wide frequency range.

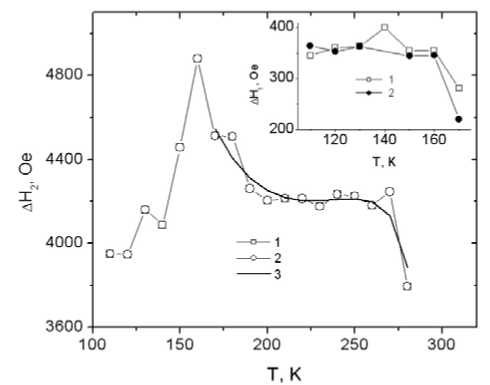
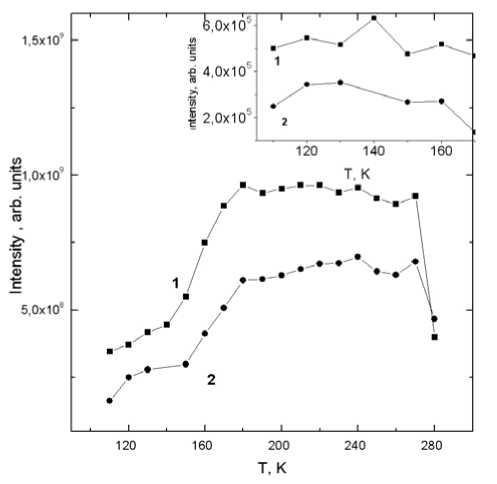
The crystal structure of the CoxMn1–xS sulfides was studied with a DRON-3 facility in monochromatic CuKα-radiation at a temperature of 300 K. According to the X-ray difiraction data, the CoxMn1–xS samples with 0

The degree of inhomogeneity of the magnetic system, the efiect of the orbital magnetic moment, and the relaxation mechanism can be established by an ESR method. Cobalt and its compounds are characterized by a high g-factor (g> 3), which is not observed in the compound under study. This confirms magnetic homogeneity of the Co_xMn_1–xS solid solutions. The magnetic resonance measurements were performed with a Bruker Elexsys 580 spectrometer at X-band frequency, using a continuous gas-fiow cryostat for He. The sample was cooled from 300 K down to 80 K in zero magnetic field and in the field H = 5 kOe. It enables to establish the dependence of the local magnetic characteristics of the sample on its magnetic prehistory and existence of degeneration on the orbital magnetic moment.

The efiective g-factor value g_eff = hн/(μ_BH_res) is determined from the resonance field, which sharply increases in the temperature range 150K<T< 180KasshowninFig. 1.

Fig. 1. Temperature dependences of the resonance field upon cooling in zero magnetic field (ZFC – 1) and in the field H = 5 kOe (FC – 2) for Co_0.05Mn_0.95S.

The inset shows the temperature dependence of g-factor (1) and relative extension of sample dL/L (2)

At T< 150 K, the g-factor is nearly temperature-independent and takes a value of about 1.3, whereas in the temperature range 190 K< T< 280 K its value varies within 1,7…1,75. Based on our data, we estimate Δg/g ~ 0.15, where g is the free-electron Lande factor and Δg is its shift in the crystalline environment.

In the absence of any appreciable static Jan–Teller distortion as observed experimentally by the X-ray difiraction data [2], one expects that the spin-orbit interaction splits the t_2g multiplet of the cubic crystal field Hamiltonian into a quadruple degenerate ground state and a higher-lying Kramers doublet. Even if a static JT distortion at the limits of the experimental error bars is included, the orbital contribution to the moment remains significant to the spin moment [5].

Antiferromagnetic long-range order causes the splitting d_xz- and d_yz-orbitals as a result of spin-orbital interaction at T< T_N, that leads to deformation octahedra. The temperature dependence of relative deformation ΔL/L for the Co_xMn_1–xS with x = 0.05 is similar to g(T) value as shown in insert to Fig. 1. These data prove a close relationship between spin and orbital magnetic moments, lattice deformation. The orbital ordered phase is characterized by an anisotropy of ΔH, which for polycrystalline samples reduces to a broad maximum in ΔH(T) [6]. For doped and pure LaMnO₃ the expression for the linewidth ESR due to crystal-field efiects and accounting only for the rotations of octahedral were obtained [7]. This theoretical approach is summarized in the formula [8]:

ΔH(T)=χ⁰(^T)×

^θ,ϕ χ(T)

⎛

τ^2β ⎜_⎜ГCEfreg(θ, ϕ) +ГCFD

^⎛TN   ^⎞

^⎜⎝6(T-TN) ^⎟⎠

⎞ ⎟fdiv(θ,ϕ)

with the free Curie susceptibility χ₀ ~ 1/T , the static susceptibility χ(T), and τ =1–T/T_JT. The first and second term describes the regular and divergent crystal field contributions, respectively. Only the latter diverges for T → T_N with an exponent α, whereas both terms decrease forT→T_JT with a critical exponent 2β. For polycrystalline compounds the averaging of angular factors f_reg(θ, ϕ), f_div(θ, ϕ) gives constant. We neglected here angular dependence ΔH(θ, ϕ) and the linewidth is well fitted by

As shown in Fig. 2 (solid line) a qualitative description was obtained by fitting the ΔH(T) data with Г_CE = 1.8 kOe, Г_CFD=0.4kOeandβ=0,14(2), α= 1,3(5) withfixedT_N= 165K, T_CW = 460 K, T_JT = 280 K. The critical indexes have been satisfactory agreement with estimates β = 0.16(1), α = 1.8 for polycrystalline LaMnO₃ [8].

Below the Neel temperature, one more weak resonance with g = 2.03 is observed in the field Hr1 whose intensity is lower than the main resonance intensity (Ir2) by three orders of magnitude (insert in Fig. 2). This resonance may be associated with spin of conductivity electron of impurity ion Co+2andmagnonsthatformative spin polaron. Spin polaron density disappears atT > TN . The ESR linewidth in the field Hr1 = 3.35 kOe below the Neel temperature is also temperatureindependent and may be related to localization of an spinpolaron with a small radius. The relaxation time is determined as 1/T1 = ω2LS ac/х [9], where ωLS is the energy of the spinorbital interaction of electron, х is the Fermi velocity of an electron (х~ 106m/s), a is the size of an localized area close to the lattice constant, and c is the concentration of the spin polaron. For example, atc= 0.001 the spin-orbital interaction is ωLS = 1012 Hz.

Fig. 2. Temperature dependences of the linewidth for the resonance field H_r2 upon cooling in zero magnetic field (ZFC – 1) and in the field H = 5 kOe (FC–2) , fitting curve (3) according to Eqn. 2 for Co_0.05Mn_0.95S.

The inset shows temperature dependence of the linewidth for the resonance field H_r1 upon cooling in zero magnetic field (ZFC – 1) and in the field H = 5 kOe (FC – 2)

Fig. 3. Temperature dependences of the ESR spectra intensity for Co_0.05Mn_0.95S sample upon cooling in zero magnetic field^.(ZFC^.–1) andinthefieldH=5kOe(FC–2) in resonance field H_r2.

The inset shows temperature dependences of the ESR spectra intensity sample upon cooling in zero magnetic field (ZFC – 1) and in the field H = 5kOe (FC –2) in resonance field H_r1

The intensity of the magnetic resonance line is determined as a product of signal amplitude anda square of linewidth H_P obtained from the distance between the absorption derivative peaks. In Fig. 3 the intensities ESR are shown to depend on the prehistory of sample. In the sample cooled in the external magnetic field H = 5 kOe, the signal intensity decreases approximately by 40…60 %. It may be explained by change of direction of magnetic moments in the unaxial antiferromagnet in the vicinity of spin-fiop field. At cooling in the field the vector AF is parallel to alternating magnetic field, that leads to absence of ESR in linear approximation.

Intensity I_r2 of the ESR in field H_r2 decreases with temperature across the phase transition paramagnetic-antiferromagnetic. In particular, in the magnetically ordered phase the ESR intensity is directly proportional to a number of magnons, I~ n ~ (S–<S^z>) or, in normalized units, I/I₀ ~ (1 – m), where mis the sublattice magnetization normalized to spin.

The absence of the temperature dependence of the linewidth (Fig. 2) in the range 190K<T<270Kallowsoneto consider the spin-orbital interaction to be the fundamental mechanism of spin relaxation and formation of short range orbital order.

Two frequencies of ESR are found in Co_xMn_1–xS solid solution below Neel temperature. These resonances are ascribed to spin polaron and spin of localized electrons. Temperature independent behavior of the ESR linewidth and temperature hysteresis of the intensity reveal at the cooling in the external magnetic field and without it in the paramagnetic state at T< 280 K, that is accounted for by formation of orbital disordered state.