Орбитальный угловой момент астигматического гауссова лазерного пучка

Лазерные пучки с орбитальным угловым моментом (ОУМ) активно исследуются в настоящее время из-за их широкого применения для оптического захвата и вращения микрочастиц [1] и холодных атомов [2], в фазово-контрастной микроскопии [3], в микроскопии со стимулированным истощением излучения [4], в оптической классической [5] и квантовой информатике [6].

Интересный лазерный пучок, который обладает ОУМ, но не имеет изолированных нулей интенсивности с фазовой дислокацией, рассмотрен в [7]. В [7] вычислили ОУМ для эллиптического Гауссова пучка, сфокусированного цилиндрической линзой. Идея использования цилиндрической линзы для придания пучку ОУМ была впервые высказана в [8]. В [8] было экспериментально показано, что пучок Эрмита–Гаусса, не обладающий ОУМ, после цилиндрической линзы на определённом расстоянии и при определённых условиях преобразуется в пучок Лагерра–Гаусса с ОУМ.

В работах [9–20] пытались получить как можно большее значение ОУМ. В [9] предложено увеличивать ОУМ с помощью набора Гауссовых вихревых пучков, центры которых расположены на окружности, а оптические оси отдельных пучков и общая оптическая ось являются скрещенными прямыми. В [9] показано, что ОУМ такого составного пучка может быть равен 204 на фотон. В [10] вместо Гауссовых пучков предлагается использовать небольшие отверстия в непрозрачном экране как точечные источники. Если их расположить в виде спирали, то в совокупности они сформируют вихревой пучок с ОУМ. В [10] практически реализован пучок с ОУМ, равным 3. В [11] показано, что при острой фокусировке оптического вихря с большим топологическим зарядом уменьшается контраст или видность боковых лепестков. В [11] практически фокусировался пучок с ОУМ, равным 15 на фотон. В [12] предложен интересный способ определения топологического заряда оптического вихря с помощью кольцевой дифракционной решётки. Экспериментально показано, что таким способом можно определить топологический заряд ±25.

В [13] экспериментально с помощью трёхволнового смешения в нелинейной среде Керра сформированы вихревые гармоники с ОУМ до 30 на фотон. В [14] практически осуществили с помощью цифрового многоэлементного зеркала (с числом микрозеркал 1024×768) генерацию идеального оптического вихря с топологическим зарядом 90. В [15] c помощью жидкокристаллического модулятора света (число элементов 1900×1200) сформировали оптический вихрь с топологическим зарядом 200, что позволило вращать микрочастицы диаметром 1,4 мкм со скоростью 500 мкм/с. В [16] также с помощью модулятора света (число отсчётов 1920×1080) сформированы перепутанные пары фотонов с ОУМ ±300 на фотон. В [17] c помощью спирального фазового зеркала, полученного в пластинке алюминия алмазным резцом, экспериментально сформирован оптический вихрь с топологическим зарядом 100. Эти же авторы [18] c помощью усовершенствованной технологии на подложке из алюминия диаметром 75 мм и шероховатостью 3 нм создали спиральное зеркало, способное формировать оптические вихри с топологическим зарядом 1020. В [18] также интерферометрически доказали, что сформированный зеркалом оптический вихрь имеет топологический заряд 5050, но форма вихря при этом существенно исказилась. В [19] c помощью электронной литографии в резисте РММА создали голограмму диаметром 80 мкм с разрешением 35 нм и высотой рельефа 25 нм, которая позволила сформировать вихревой пучок электронов с энергией 0,5–1 эВ с топологическим зарядом 1000. И, наконец, в [20] с помощью спирального алюминиевого зеркала диаметром около 50 мм для длины волны 810 нм сформированы фотоны, перепутанные по ОУМ и поляризации. Причём квантовый ОУМ фотонов был равен ± 10010. Это максимальное значение ОУМ, полученное на сегодняшний день.

В данной работе, следуя работе [7], мы покажем, что эллиптический Гауссов пучок после цилиндрической линзы, ось которой не совпадает с осями эллипса Гауссова профиля, при распространении вращается и не является вихревым лазерным пучком. Хотя его полный ОУМ может достигать больших значений пу- тём изменения радиусов перетяжки эллиптического Гауссова пучка и фокусного расстояния цилиндрической линзы. Рассчитаны коэффициенты разложения комплексной амплитуды такого астигматического Гауссова пучка в ряд по угловым гармоникам. Также получена точная формула для ОУМ в виде ряда по функциям Лежандра второго рода.

1. Безвихревой пучок с ОУМ

В этом параграфе для удобства читателя первые четыре формулы совпадают с [7]. Обычно рассматриваются параксиальные вихревые лазерные пучки, обладающие ОУМ. У таких пучков есть точки сингулярности – это изолированные нули интенсивности, в которых фаза не определена и вокруг которых изо-фазная поверхность волнового фронта имеет спиральную форму. Но, оказывается, есть простые световые поля, которые обладают ОУМ и не имеют изолированных нулей интенсивности с вихревой фазой. Рассмотрим Гауссов эллиптический пучок, в перетяжке которого расположена цилиндрическая линза [7]. Комплексная амплитуда света сразу за цилиндрической линзой имеет вид:

E ( x , y ) = exp

x ²

V

w ² x

2 A y

w ² X

x

I ikx cos a x exp--

V 2 f

iky ² sin² a ikxy sin 2 a

2 f 2 f

тичности пучка (1), тем больше его ОУМ. Знак ОУМ определяется тем, по какой оси, y или x , больше вытянут Гауссов пучок в перетяжке. Преимущество пучка (1) в том, что он может быть реализован без дополнительных элементов, без модулятора света, спиральной фазовой пластинки или голограммы с «вилочкой». Для его формирования надо всего две цилиндрические линзы, одна из которых формирует эллиптический Гауссов пучок, а вторая – создаёт ОУМ.

Оценим величину ОУМ для конкретных значений величин, входящих в (4). Гауссов пучок считается параксиальным, если радиусы его перетяжки больше длины волны, пусть они будут равны w x =2 мм и w y = 1 мм, фокусное расстояние пусть будет равно f = 10 мм, а длина волны λ =0,5 мкм, наклон линзы равен 45° ( a =п/4). Тогда ОУМ в (4) будет равен 471,24.

В Приложении 1 показано, что использование двух скрещённых цилиндрических линз с одинаковыми фокусными расстояниями, но имеющих разные знаки, увеличивает нормированный ОУМ в 2 раза.

В Приложении 2 получены формулы, описывающие прохождение поля (1) через ABCD-систему, и получена общая формула для плотности ОУМ астигматического Гауссова пучка на любом расстоянии от плоскости перетяжки.

В Приложении 3 получено выражение для полного ОУМ астигматического Гауссова пучка (1), если цилиндрическую линзу размещать не в перетяжке, а в любой другой плоскости при распространении пучка.

где w x и w y – радиусы перетяжки Гауссова пучка по декартовым осям, f – фокусное расстояние тонкой цилиндрической линзы, образующая которой имеет угол с вертикальной осью y , равный a (линза повернута против часовой стрелки), k – волновое число света. Нормированный ОУМ в параксиальном случае вычисляется по формулам [7] (c точностью до постоянных):

Г Г             ^d E ( ^x , У )     ^d E ( ^x , У )

J z = Im     E ( x ,y ) l x------y-------- I dx d y , (2)

d y         d x

—Г —Г

Г Г

W = J J E ( x , y ) E ( x , y ) d x d y ,                       (3)

—Г — Г где Jz – проекция ОУМ на оптическую ось, W – плотность энергии (мощности) света, Im – мнимая часть числа, E – комплексно сопряжённая амплитуда к амплитуде (1). Подставляя (1) в (2) и (3), получим простое выражение для нормированного ОУМ светового поля (1):

J_z ( k sin2a\

= w 2 — Wx ² .                         (4)

W V 8 f J^{v y x}’

Из (4) видно, что ОУМ равен нулю, если Гауссов пучок имеет круглое сечение ( w x = w y ) или линза не имеет наклона к вертикальной оси ( a =0). При наклоне в 45 градусов ОУМ (4) максимальный при прочих равных условиях. Из (4) также видно, что ОУМ пучка (1) в общем случае дробный, хотя может быть и целым. Чем меньше фокусное расстояние цилиндрической линзы, тем больше ОУМ пучка, и чем больше степень эллип-

• 2 . Орбитальный угловой момент астигматического пучка

Чтобы наглядно показать формирование ОУМ, ОУМ пучка (1) в данном параграфе будет рассчитан другим способом, основанным на разложении амплитуды поля (1) в ряд по угловым гармоникам. Разложим амплитуду (1) в полярных координатах ( r, φ) E ( r , ф ) = exp ( — ar ² cos² ф — br ² sin² ф — icr ² sin2 ф ) , (5)

в ряд по угловым гармоникам:

E ( r , Ф ) = S C n ( ^r )exP( in ф ), n =—r

2n

где Cn (r) = ( 2n) 1 J E (r, ф) exp (— inф) dф, а также a = w— + ik (2 f) 1 cos2 a, b = w— 2 + ik (2 f) 1 sin2 a, c = k (4 f) 1 sin 2a.

Интеграл (7) можно переписать в виде:

Cn (r ) = (2n)—1 e—D x

2n xJ exp(—inф — Acos2ф — iBsin2ф)dф,

где A = [( a – b )/2] r ² , B = cr ² , D = [( a + b )/2] r ² . После замены t =2φ, и с учётом чётности номера n =2 m , вместо (9) получим:

2п                                                                          ( Z7 Л m

C„ ( r ) = (2 л ) " ¹ e" D f exp ( - imt - A cos t - iB sin t ) d t = ( - i ) m e" D ^{+ im 6} J_m ( F ) = e" D I------I J_m ( F ), 0                                                V A - B J

где F = ( B ² - A ² ) ^1/2 , tg 6 = iBIA . Для нечётных номеров угловых гармоник n = 2 m +1 коэффициенты (9) будут равны нулю:

2п

2 п C 2 m +1 ( r ) = e ^- D J exp [- i ( 2 m + 1 ) ф- A cos2 ф- iB sin2 ф] d ф = 0

П

= e ^- D <  J exp [- i ( 2 m + 1 ) ф- A cos2 ф- iB sin2 ф] d ф + l о

n

+ J exp [-i (2m + 1) (ф + n) - A cos 2 (ф + n) - iB sin 2 (ф+ n)] dф ^ = о                                                                                                     J

= e ^- D J [ 1 + ( - 1 ) 2 m ^{+ 1} ] exp [- i ( 2 m + 1 ) ф- A cos2 ф- iB sin2 ф] d ф = 0. 0

Тогда для коэффициентов (9) получим:

C n ( r ) =

e

D

F

A - B

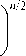
J 2 ( F ) ,

n = 2 m ,

7          d , D m

C 2 m = J eA B J m ( F )|’ r d r =

0       ^{A B}

0,

n = 2 m + 1.

Из (12) видно, что коэффициенты при угловых гармониках с положительными и отрицательными номерами различаются по модулю ( n = 2 m ):

I C 2 m ( r )p = e D

I C -2 m ( r )² = e -^2Re D

a - b + 2 c	m
a - b - 2 c

^

J e ^{- Re (} a ^{+ b} ) ^{r 2} J m ( Gr ² ) J m ( G * r ² ) r d r = (16) 0

1 a - b + 2 c

2 a - b - 2 c

m ^

j e - ^{Re (} a ⁺ b ) u j m ( Gu ) j m ( g. _u ) d _u ,

A + B

A - B

m

J m ( F )²,

A - B

A + B

m

J m ( F )².

где G = [4 c ² –( a – b ) ² ] ^1/2 /2.

Интеграл в (15) можно вычислить с помощью справочного [21] интеграла

Нормированный ОУМ для разложения (6) можно представить в виде выражения:

7      2                             .-,           (      p ² I

J ^e~p J m ( qr ) ^{r d r} = ( ^{2 n} q ) Q m - 1/2 1 ^{1 +}yr I , ⁽¹⁷⁾

о                                     V ^{2 q} J

где

J _z

W

E nCn n=-7_____

7         ,

E Cn n=-7

C n = J C ( r )|² r d r . 0

Далее полагаем a = п /4, чтобы a - b было вещественным и можно было убрать знак модуля у квадрата функции Бесселя. Коэффициенты в сумме (14) для чётных номеров имеют вид:

С =

2 m

a - b + 2 c a - b - 2 c

m

x

x J exp [- Re ( a + b ) r ² ] x

для вычисления интеграла в (16) можно также использовать справочный интеграл [21]:

J e ^{- px} J _v ( bx ) J _v ( cx ) d x =

П V bc

Q   I p ² + b ² + c ² 1

^{Uv- 1}1² V      2 bc      J ,

где Q v ( x ) – шаровая функция или функция Лежандра 2-го рода ( x > 1):

Q _v ( x ) = Vn ( 2 x ) ^-v- 1 Г ( v + 1 ) Г "* ( v + 32 ) x

^X 2 F 1

v +1 v + 2     3_

,, v + -,

2    22

где Г (x ) - гамма-функция, ₂ F ( a , b , c , x ) - гипергеометрическая функция [22]. Тогда вместо (15) можно записать:

2 m

m

I c + a - b I = n I----------I x

V с - a + b J

² m

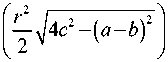
Г                     2 ""I-1/2

^{x [ c 2 -} ( a ^{- b} ) ^] Q m -1/2

1 ₊ ^{2 (} a ^{+ b ) 2} c ² - ( a - b ) 2

или для общего случая угла наклона a ^ п /4 вместо

(20) получим:

C 2 m

1 a - b + 2 c

2 п G a - b - 2 c

x

^{x Q} m \- 12

' Re² ( a + b ) + 2Re G ²

I        21 G2        J

.

Пусть | G | ² ≈ 0. Тогда аргумент функции Лежандра в (21) стремится к бесконечности, и из асимптотики функции Лежандра при x >> 1 [22]

Q v ( % ) = ТЛ ( 2 % ) ^{-M- 1} Г (|v| + 1) Г -¹ (|v| + 3/2) (22)

следует выражение для коэффициентов разложения в формуле для ОУМ (14):

- =    1    Г (|m\ +x2m 22m+1 Зя Г (I m| +1)

|a - b + 2 c m ^{+ m}\ a - b - 2 c m ^- m

^X         Re²¹ m ^{+ 1} ( a + b )

ми номерами: C _{2 m} >  C __{2 m} . То есть больший вклад в ОУМ будут давать угловые гармоники exp( i 2 m φ) c положительными номерами, и значит, ОУМ >0. Если, наоборот, a - b <  0 или W y <  w % и f ^{- 1} <  z - y - z - ) , тогда C _{2 m} <  C _{- 2 m} и ОУМ <0. Эти выводы согласуются с формулой (4).

Таким образом, мы показали, что эллиптический Гауссов пучок с астигматизмом (1) обладает ОУМ (14), в который дают вклад только все чётные угловые гармоники как с положительным топологическим зарядом 2 m , так и отрицательным –2 m , хотя их вклады разные по величине C _{2 m} ^ C _{- 2 m} . Причём при m = 0 коэффициент C ₀ отличен от нуля и равен:

C 0 =

п Дc ² - ( a - b )²

^Q -1/2

1 +

2( a + b )² c¹ - ( a - b )²

Заметим, что аргумент функции Лежандра в (20) комплексный. Далее для определённости опять пусть цилиндрическая линза повернута на угол а , равный 45 градусам. Когда Гауссов пучок круглый ( w y = w x ), тогда в (20) a – b =0, и коэффициенты (20) при угловых гармониках с номерами m и – m равны, то есть ОУМ (14) равен нулю. При 2 c = b – a , или когда f "1 = z о ^- 1 ^- z о ^- % ⁽ z о % = kwH^2, z 0 y = kwy)^{2 -} Длины Рэлея), все коэффициенты (20) при m >0 равны нулю, а при m <0 коэффициенты (20) отличны от нуля:

Значение функции Лежандра в (27) можно получить через полный эллиптический интеграл [22]:

Q-1/2 (%) = л       K | л |, v 1+% v v 1+% j

.-1/2

K ( t ) = J [ (1 - % ²)(1 - 1% ²) J    d % .

C 2 m

0, m >  0,

= ^ f Г (Im| +12) (

2 .     2

wy + wx yx

x -2| m |-1

k^ Г(|m| +1) v

^w % ^{- w} 2 7

, m <  0.

При этом ОУМ (14) отличен от нуля. Если же, наоборот, 2 c = a - b , то есть f ^{- 1} = z - % - z - y , то все коэффициенты при m <0 равны нулю, а при m >0 коэффициенты (20) отличны от нуля:

2 m

f Г ( m + 1/2 ) k 4к Г ( m + 1 )

х   .      9 3 2 m 1

[     wJV  y    % 7

, m >  0,

0, m <  0.

При этом также ОУМ (14) отличен от нуля. Из (25) видно, что коэффициенты | C _n | ряда (14) с увеличением номера убывают до нуля. При больших m вместо (25) можно записать ( m >0):

C2 =

2 m

f

/ 2      2 ^2 ^m +1

w y ^{- w} %

k Vn m w_v + w_x yx

Далее пусть для определённости a – b >0 или

W y >  w % , и пусть c >  a - b , то есть f ¹ >  z „ y - z ₀ ) . Тогда

коэффициенты (20) с положительными номерами m >0 будут больше коэффициентов с отрицательны-

3. Моделирование

Проверим численно полученные выше соотношения. Рассчитаем ОУМ по исходной формуле (4) и по формуле через разложение по угловым гармоникам (14). Параметры расчёта: длина волны % = 532 nm, угол наклона цилиндрической линзы а = п /4, радиусы перетяжки эллиптического Гауссова пучка w % = 20 % и W y = 400 % , фокусное расстояние цилиндрической линзы f =1/(1/ z 0 % -1/ z 0 y ) = 1260 % . Распределение модулей коэффициентов | C _n | показано на рис. 1 (сплошная кривая). Для других радиусов перетяжки w % =10 % , w y = 100 % и фокусного расстояния цилиндрической линзы f = 1 / (1/ z 0 % -1/ z 0 y ) = 317 % распределение модулей коэффициентов C _n в формуле (14) показано на рис. 1 (прерывистая кривая).

Для первого случая (сплошная кривая на рис. 1) ОУМ, рассчитанный по формуле (4), равен 99,500625, а ОУМ, рассчитанный по формуле (14), равен 99,48454. Для второго случая (прерывистая кривая на рис. 1) ОУМ, рассчитанный по формуле (4), равен 24,5025, а ОУМ, рассчитанный по формуле (14), равен 24,5025. Во втором случае видим совпадение с точностью до четырёх знаков после запятой. В расчёт е по формуле (14) было учтено 2000 коэффициентов | C _n | . Из рис. 1 видно, что чем меньше ОУМ, тем меньше величина отличных от нуля к о эффициентов разложения по угловым гармоникам | C _n | (прерывистая кривая под сплошной кривой).

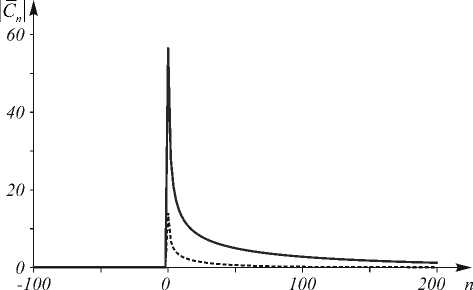
Рис. 1. Распределение | C_n | (только чётные номера, нечётные равны нулю) для двух разных пучков и фокусных расстояний цилиндрической линзы: W x = 20 1 W y = 400 1 f= 1260 1 (сплошная кривая); W x = 10 1 W y = 100 1 f= 317 1 (прерывистая кривая)

через две скрещенные цилиндрические линзы с разным фокусным расстоянием f x , f y , оси которых наклонены под углом а к горизонтальной оси. Комплекс -ная амплитуда такого поля в начальной плоскости

( z =0) имеет вид:

E ( ^x , y ) = exp

^^^^^^s

V

x ²

w ² x

^^^^^^s

y ² w y ²

^^^^^^е

ikx '²    iky '²

2 f x

^^^^^^е

2 f У

(А1)

где

[ x ' = x cos а + y sin а ,

[ y = y cos ае x sin а .

(А2)

Тогда, подставив поле (А1) в (2), (3), можно найти нормированный ОУМ:

z

W

1 Y

-- ( W ²

8 V f y f x J^{( x}

k

^^^^^^е

е w - ) sin 2 а .

(А3)

Заключение

В работе мы получили следующие результаты. Для астигматического Гауссова пучка, который формируется при фокусировке эллиптического Гауссова пучка цилиндрической линзой, получено выражение для нормированного ОУМ в виде ряда из функций Лежандра второго рода с полуцелыми номерами. Если параметры эллиптического Гауссова пучка и цилиндрической линзы удовлетворяют условию f ¹ = z 0y - z - Г , то вклад в ОУМ вносят только угловые гармоники с отрицательными топологическими зарядами 2 m <0. И, наоборот,

-1      -1      -1

если имеет место условие f = z _{0 x} - z ₀ y , то вклад в ОУМ вносят только угловые гармоники с положительными чётными номерами 2 m >0. Во всех случаях самым большим по величине будет нулевой коэффициент в разложении астигматического поля по угловым гармоникам. Но так как этот коэффициент умножается на ноль (нулевой топологический заряд), то он не даёт вклад в ОУМ. Но из-за большого вклада нулевой угловой гармоники в амплитуду астигматического поля в распределении интенсивности этого поля нет изолированных нулей, и поэтому точек с сингулярной фазой. Такой астигматический пучок выглядит как безвихревой, хотя он обладает ОУМ.

В трёх Приложениях мы получили: 1) явное выражение для нормированного ОУМ астигматического Гауссова пучка, сфокусированного двумя скрещенными цилиндрическими линзами (собирающей и рассеивающей); этот пучок имеет больший ОУМ, чем сфокусированный только одной собирающей; 2) явную формулу для нормированной плотности ОУМ астигматического Гауссова пучка, прошедшего ABCD-систему; 3) явную формулу для нормированного ОУМ для астигматического пучка, если цилиндрическая линза расположена не в перетяжке эллиптического Гауссова пучка, а на произвольном расстоянии от перетяжки.

Приложение 1

Рассмотрим вместо поля (1) более общее световое поле, когда эллиптический Гауссов пучок проходит

Из сравнения (А3) с (4) видно, что если фокусные расстояния цилиндрических линз имеют разные знаки (одна линза собирающая, а другая – рассеивающая), то ОУМ можно увеличить в 2 раза по сравнению с использованием только одной цилиндрической линзы.

Приложение 2

Рассмотрим распространение поля (А1) через ABCD-систему, тогда для комплексной амплитуды на выходе можно получить выражение:

E ^{2 (6} , ^П) = BiG ^X

ikD <,г

^X exp -( 6 ⁺ⁿ )

где

P xx

P yy

Р xy

^^^^^^е

k ² P xx n ² + P yy 6 2 е P xy 6n

B ²

G

,

(В1)

1 ik ik

= —- +---cos а +---sin а w2  2f xx

2 f y ik

1 ik

= —+ _ sin ай

wy ik

2 f x

2 f y

cos2

^^^^^^е

ikA

2 B ,

а е

ikA

2 B ,

(В2)

i

— sin 2 а , G = 4 PP

Iff          y

V f^x f y 7

^^^^^^е

xx yy

² xy .

Распределение интенсивности поля (А1) на де ABCD-системы будет иметь вид:

k ²

I 2 ^ ^ В ^ ‘"p

^^^^^^е

2 k * ( 6 , n ) , В ² | G|

выхо-

(В3)

где

*(6, n) =

= Re { P yy G * } 6 ² + Re { P „ G * } n 2 е Re { P ,y G * } 6n

Из (В3) видно, что интенсивность имеет вид эллиптического Гауссова пучка, как и в начальной плоскости (А1). Из формулы (В1) можно получить формулу для плотности ОУМ в полярных координатах ( r, ф ) на любом расстоянии z при условии, что цилиндрическая линза только одна с фокусным расстоянием f x , а также f y ^да, а = п /4, A = 1, В = z :

;        2z„ z„ \fz 2+z„z„ (z- f ) Icos2(p + f (z 2 -z,2 )z(z-2f )sin2

I ^E 2 |^{2                   4} _ ^fx^Z 2 ^{+ Z} 0 x ^Z 0 y ( ^Z — ^f x ) J ^{2 +} ( ^Z 0 x ^{+ Z} 0 y ) ^{2 Z} 2 ( ^Z — ^{2 f} x ) 2

(В4)

где z.. = kw2/2, z„,, = kw,2 /2 - длины Рэлея. В част-0x        x        0y        y ном случае на двойном фокусном расстоянии из (В4)

следует простая формула для плотности ОУМ:

j _z E 2 ²

k      z 0 x z 0 y

2 f x 4 f x ² + z 0 x Z 0 y

r ²cos2 ^ .

(В5)

Из (В4) следует, что нормированная плотность ОУМ зависит от расстояния до линзы z . Причём числитель пропорционален z ² , а знаменатель – z ⁴ . То есть плотность ОУМ (В4) убывает с расстоянием квадратично, так же, как убывает интенсивность Гауссова

пучка из-за его расходимости.

Приложение 3

Раccмотрим эллиптический Гауссов пучок (1) не в плоскости перетяжки, а в любой другой плоскости на расстоянии z от плоскости перетяжки. Комплексная амплитуда на расстоянии z от перетяжки пучка (1) будет иметь вид:

E ( x , y , ^z ) = _ q x ( ^z ) q y ( ^z ) ] 1 ^{2 x}

равен нулю, так как на этом расстоянии эллиптический Гауссов пучок имеет круглое сечение. Если z <  kw x w y /2, ОУМ положительный, если z >  kw x w y /2, то отрицательный. При больших z ОУМ растёт по модулю квадратично от z . Хотя заметим, что при ранее выбранных параметрах Гауссова пучка ( w x =2 мм, w y = 1 мм, λ =0,5 мкм), расстояние, на котором ОУМ от максимального (при z =0) уменьшается до нуля, равно z =4π метров. Поэтому для получения максимального ОУМ следует помещать цилиндрическую линзу в перетяжку эллиптического Гауссова пучка.

Работа поддержана грантом Российского научного фонда № 17-19-01186.

x exp

V

^w 2 q x ( ^z )

где

y ²

(С1)

^w 2 q y ^{( z} ) ,

qx (z ) =1+i^- ,  qy (z ) =1+—, z0x                     z0y

(С2)

а длины Рэлея – как в (В4). Если в поле (С1) поместить цилиндрическую линзу с фокусным расстоянием f , образующая которой повёрнута в поперечной

плоскости на угол а , комплексная амплитуда света сразу за цилиндрической линзой будет иметь вид:

E ⁽ x , y , ^z ) = _ q x ( ^z ) q y ( ^z ) ] ^{1/2 x}

x exp

x ²

y ²

V

w 2 q x ( ^z ) w y q y ( ^z )

x

(С3)

x exp

ikx ² cos ² a   iky ² sin² a ikxy sin 2 a

2 f

2 f

2 f

.

Нормированный ОУМ пучка (С3) имеет вид:

J_z / k sin2a\ ₂1 |²     21 |2\

W 7 = V -"8 f -J ( w y l ^q y | - w x l ^q x | ).             ^(С4)

Из (С4) видно, что знак и величина ОУМ зависит от расстояния z от перетяжки эллиптического Гауссова пучка до плоскости размещения цилиндрической линзы. Это более ясно видно, если записать (С4) в другом виде:

J _z

W

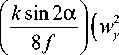
w ² x

) ^{1 -}

4 z ²

V

k ² w 2 w 2

xy

(С5)

Из (С5) видно, что если цилиндрическую линзу поместить на расстоянии z = kw x w y /2, то ОУМ будет